基于双重移相控制的双有源桥DC-DC变换器的软开关

王 聪 沙广林 王 俊 庄 园 程 红

基于双重移相控制的双有源桥DC-DC变换器的软开关

王 聪 沙广林 王 俊 庄 园 程 红

（中国矿业大学（北京）机电与信息工程学院电气工程系 北京 100083）

通过分析双重移相控制下双有源桥DC-DC变换器的工作模式与各桥臂IGBT实现软开关的约束条件，得出了满足软开关条件的高频变压器漏感参数设计方法与死区时间限制条件；根据变换器稳态运行各阶段电路状态数学模型的分析，实现了通过对电路参数的优化设计降低变换器开关损耗，从而提高双有源桥直流变换器的效率。最后，根据理论推导结果设计变压器漏感并试验，试验结果表明所提出的设计方法对增加软开关实现范围和提高变换器效率的有效性。

双有源桥直流变换器 双重移相控制 软开关 死区时间 效率

1 引言

近年来，高频隔离双向多电平变换器作为中高压电网接口装置替代传统的线性工频变压器，成为电力电子学科的研究重点。究其原因，是其在构建下一代中压功率变换系统[1]、UNIFLEX[2]项目、FREEDM[3]系统等研究中所体现出的巨大潜力。文献[1-3]讨论了一种典型的高频隔离双向多电平变换器结构，这种变换器由两侧的级联多电平整流/逆变级，中高频隔离双向直流变换器的三级结构组成。双向隔离DC-DC变换器作为此种多电平变换器的功率传输级，提供电气隔离的同时，对提高高频隔离双向多电平变换器的功率密度起到极其关键的作用[1]。

众多双向隔离DC-DC变换器结构中，双有源桥DC-DC变换器因其高功率密度、零电压开关、双向能量传输、模块化、双向对称结构与简单的控制实现而备受关注[4-6]。单移相控制作为一种有功功率控制算法，是双有源桥DC-DC变换器普遍采用的控制方法[7]。但单移相控制不仅在功率调节方面缺乏灵活性，而且增大了稳态情况下变换器中开关管的电压应力[8-9]。为了提高单移相控制下变换器性能，文献[8-9]提出了采用双重移相方式提高直流变换器的功率容量，降低回流功率；然而双重移相控制中滞后桥臂开关管开关动作时刻，电感电流更加接近零，造成滞后桥臂开关管软开关区域变小，反而增大了开关损耗。针对以上问题，文献[10-12]提出了一种在满足软开关条件的基础上，通过限制移相角度实现给定传输功率下基于最小回流功率的控制方法。根据双重移相控制下双有源桥DC-DC变换器传输功率的数学模型可知[13]，移相控制通过调节双有源桥DC-DC变换器桥间与桥内移相角控制变换器传输功率，因此这种通过限制移相角降低开关损耗与开关管应力的方法也限制了直流变换器的动力学性能。无论是通过改变移相控制方式还是通过对移相角的限制来降低回流功率从而减小损耗，都是在分析软开关区域的基础上实现的。然而上述所有分析方法都没有从影响软开关区域的角度分析软开关实现条件。文献[14-15]都讨论了开关死区时间对双有源桥DC-DC变换器效率的影响，通过理论分析与多组试验结果比较得出死区时间的优化结果，并指出死区时间是影响双有源桥DC-DC变换器传输功率和运行状态的重要因素，可以通过调制策略与硬件参数的合理设计消除其影响。

不同于将双向DC-DC变换器输出直流等效为负载或者恒流源，本文以高频隔离双向多电平变换器的功率传输级双有源桥DC-DC变换器作为研究对象，双向直流变换器输入与输出侧连接的级联整流与逆变级等效为电压源。通过分析双重移相控制双有源桥DC-DC变换器各工作状态特性与实现软开关过程，参考传统单向直流变换器的特性[16]，建立关于高频变压器电压与电流的数学模型，得出满足软开关条件的硬件参数设计与死区时间设置范围。

2 双重移相控制理论与软开关技术分析

2.1双重移相控制原理

双重移相控制下双向直流变换器工作模式大致分为图1所示三种状态，图1b中iL(t1)=0时发生开关动作不可能实现零电压导通与软关断；图1a工作模式中，t6(t0)时刻一次侧电流的绝对值开始变小，t1时刻前一次侧电流已经由负值过零，S2开关动作不能反向导通，因而一次侧电流过零后一直为零直到t1时刻，与图1a工作模式不符；本文重点分析图1c模式下，考虑snubber电容充放电过程的软开关实现条件。

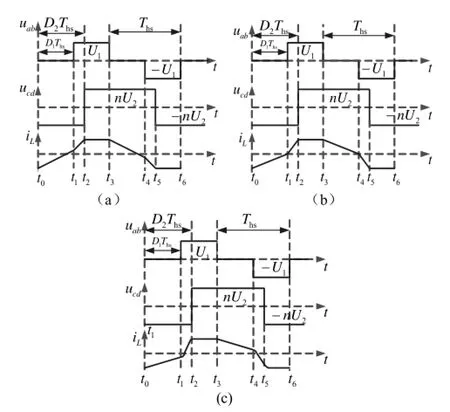
图1 双重移相控制下双向DC-DC变换器波形图Fig.1 Waveforms of bidirectional DC-DC converter controlled by dual-phase-shifting

2.2双重移相控制下变换器工作模式

为了探究双重移相控制下双向DC-DC变换器稳定状态下实现软开关技术的条件，假设变换器已工作于稳定状态，分析图1c所示的工作原理波形。t6(t0)时刻之前，S2，S3导通，Q2，Q3的续流二极管导通。

（1）t6(t0)～t0res阶段:t6(t0)时刻，S3关断，由于C3端电压不能突变，S3实现零电压关断，之后一次侧电流iL(t)以谐振方式对C3充电，对C1放电直至t0res时刻C1上的电压下降为零。此阶段电路状态可用如下方程表示为

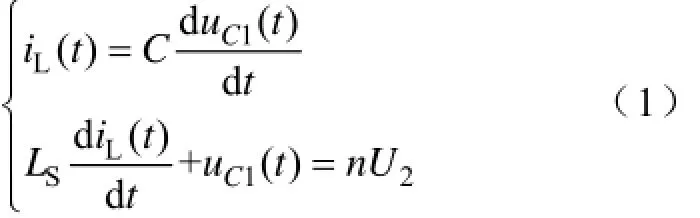
初始条件:uC1(0)=U1，iL(0)=-Ip，C=C1+C3，则

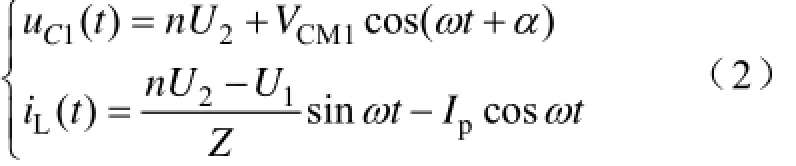
（2）t0res～t1阶段:HB1一次侧电流iL(t)通过S1的反并联二极管D1，S2以及高频变压器一次侧，将变压器漏感LS储存能量通过变压器二次侧HB2中反并联二极管M2与M3传输至电源U2，这个阶段一次侧电流iL(t)可表示为

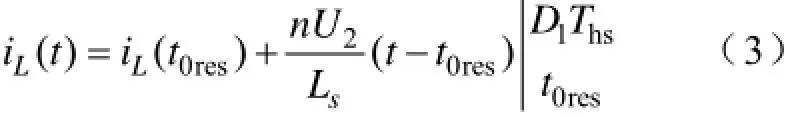
（3）t1～t1res阶段:t1时刻S2关断，一次侧电流iL(t)从S2中转移到一次侧C2和C4支路中，给C2充电，同时C4被放电，由于C2和C4保证S2是零电压关断，同时LS串联在电路中，与C2和C4产生谐振。此时变压器二次侧等效为nU2直流电源，在这个阶段有

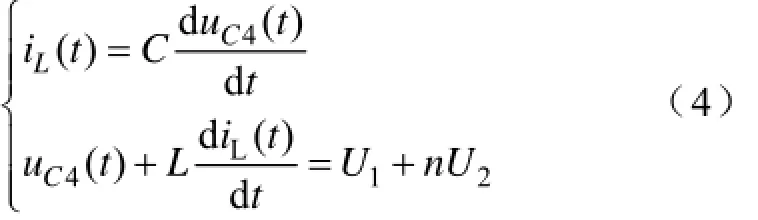
初始条件:C=C2+C4，uC4(0)=U1，iL(0)= -Im，则

（4）t1res～t1′阶段:t1res时刻，C4的电压降至零，为实现S4零电压开通，需保证一次侧电流iL(t1res)＜0，S4反并联二极管D4自然导通后开通S4，则此时S4电压为零，因而S4零电压开通，但并没有正向电流流过；t1′时刻，一次侧电流变为零，即iL(t1′)=0。

一次侧电流iL(t)可表示为

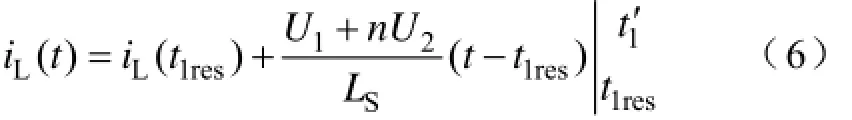
（5）1t′～t2阶段:一次侧电流由负值过零，并且向正方向增加，此时S1与S4为一次侧电流提供回路。1t′～t2阶段内一次侧电流的表达式与式（6）式相同，其中iL(t2)=-iL(t5)=Iq，且iL(t1′)=0，则iL(t)还可表达为

（6）t2～t2res阶段:t2时刻，Q2与Q3关断，二次侧电流由二次侧电容C1，C2与C3，C4两条并联线路与二次侧等效漏感串联产生谐振，二次侧谐振电流抽走C1与C4上的电荷，同时又给C2与C3充电直至t2res时刻C1与C4上的电压下降为零。由于C2与C3的电压不能突变，Q2与Q3同样零电压关断。谐振阶段一次侧电流可表示为

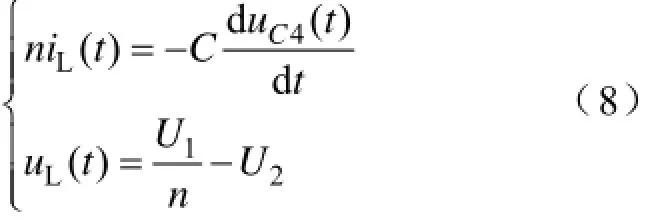
初始条件:C=C2+C4=C1+C3，uC4(0)=U2，iL(0)=Iq，uC1(t)=uC4(t)，则

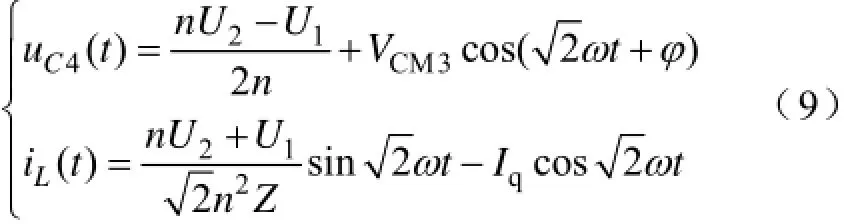
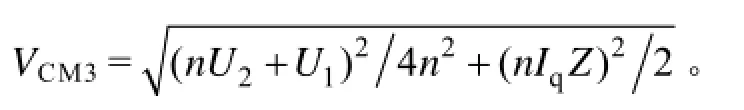
（7）t2res～t3阶段:功率由U1传向U2，是变换器正半周期传输功率的主要阶段，其中iL(t3)=Ip。

（8）t3～t3res阶段:t3时刻，S1关断，一次侧电流由U1，C1与C3并联线路与LS，S4组成谐振电路对C1充电，C3放电直至t3res时刻C3上的电压下降为零。由于并联snubber电容C1的存在，S1实现零电压关断。变压器二次侧等效为nU2电压源与漏感LS串联，通过snubber电容C1与C3产生谐振电路，这个阶段谐振电路应满足方程

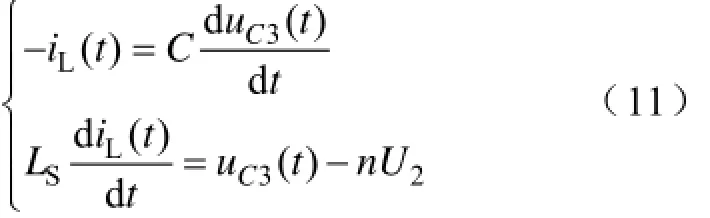
初始条件:uC3(0)=U1，iL(0)=Ip，C=C1+C3，则

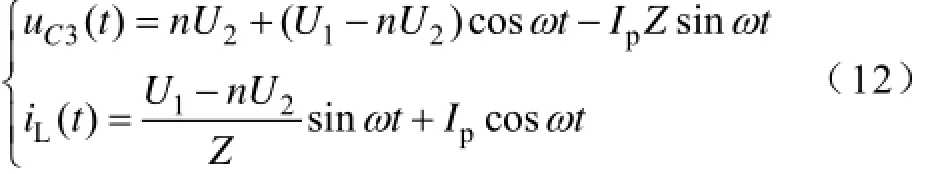
（9）t3res～t4阶段:t3res时刻C3上的电压下降为零，D3自然导通，从而保证S3零电压开通；t3res～t4阶段，U1对Cdc1储能，漏感LS储存的能量通过由D3，S4与变压器二次侧构成回路向U2传输功率，其中，iL(t4)=-iL(t1)=Im，一次侧电流iL(t)为

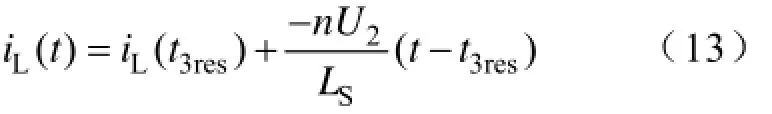
（10）t4～t4res阶段:t4时刻，S4关断，一次侧电流通过由U1，C2与D3，C4并联线路与LS，变压器一次侧组成谐振电路对C4充电，C2放电直至t4res时刻其电压下降为零；t6(t0)～t0res阶段与t3～t3res阶段为正负半周对称阶段，相似的，t4～t4res阶段与t1～t1res阶段有对称的表达式为

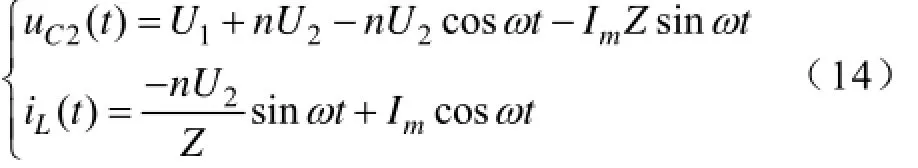
其中，uC2(0)=U1，iL(0)=Im。

（11）t4res～t4′阶段:为保证S2零电压开通，需要保证一次侧电流iL(t4res)＞0使D2自然导通；t4res时刻漏感的储能通过D2，D3与U1组成回路继续向U1与U2两侧释放能量，直到t4′时刻一次侧电流为零，即iL(t4′)=0。这个过程中iL(t)可表示为

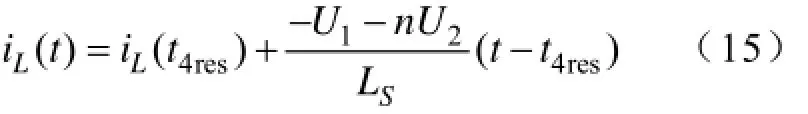
（12）4t′～t5阶段:4t′时刻一次侧电流由正值过零，并且向负方向增加，S2，S3与Q1，Q4正向导通,一次侧电流的表达式与t4res～4t′阶段iL(t)表达式相同，其中，iL(t5)=-Ip。

（13）t5～t5res阶段:t5时刻，变压器二次侧变换器Q1，Q4关断，通过四个开关管的snubber电容与二次侧等效漏感产生谐振电路完成零电压关断过程，此阶段电路的谐振方程与（9）对称:

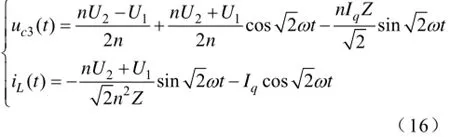
式中，uC2(0)=U1，iL(0)=-Ip，uC2(t)= uC3(t)。

（14）t5res～t6阶段:变压器二次侧电流跟随一次侧电流持续负向增大，t5res时刻电容放电结束后寄生二极管D2，D3自然导通

由于前后半周期工作状态对称，表1为双重移相控制下双向DC-DC变换器半周期内运行中各开关管与反并联二极管的运行通断状态，并概括了各个运行阶段电路运行状态与功率传输状态。

2.3双重移相控制下变换器软开关实现条件

通过双重移相控制下双向DC-DC变换器工作模式的分析可知，高频变压器两侧H桥IGBT软开关过程不同；变压器一次侧H桥两个桥臂的开关管的软开关条件也有差异。根据上节对一个控制周期的分析，各时刻可表示为t1=D1Ths，t2=D2Ths，t3=Ths， t4=D1Ths+Ths；-iL(t1)=iL(t4)=Im，iL(t1′)=0，iL(t2)= -iL(t5)=Iq，iL(t4′)=0，iL(t3)=-iL(t0)=Ip；开关频率fs=1/2Ths。

稳定状态下，级联变换器始终保持U1≈nU2，因而本文以U1=nU2进行讨论。

2.3.1 高频变压器一次侧软开关实现

为了完全实现软开关（ZVS）技术，需要保证开关管发生开关动作时，高频变压器漏感能量足够大，使关断与即将开通的IGBT的snubber电容能量交换得到保证。变压器一次侧S1与S3所组成桥臂为超前臂，S2与S4所组成桥臂为滞后臂，超前臂分别在t0/t6与t3时刻发生开关动作、滞后臂分别在t1与t4时刻发生开关动作，由于超前臂与滞后臂发生开关动作的两个时刻电路状态是正负对称的，因而分别分析其中一个时刻的软开关条件即可满足要求。

表1 双重移相控制下双有源桥DC-DC变换器周期运行状态Tab.1 The operating states of DAB DC-DC converter in dual-phase-shifting control in each duty cycle

由图2c容易得出，Ip＞Im，因而超前臂更容易实现软开关。根据式（2）可知，为保证uC1(t)的电压能谐振下降到零，应满足:VCM1≥nU2，整理可得超前臂开关管零电压开通条件为

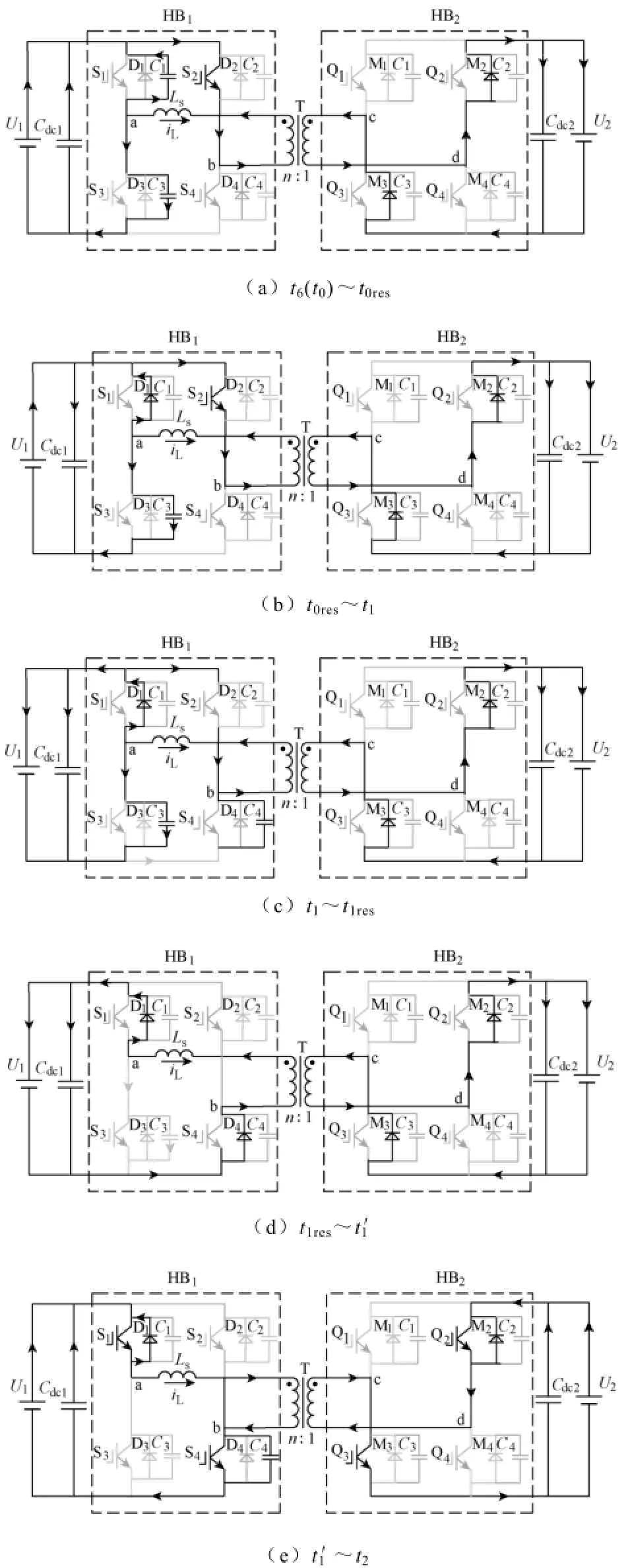
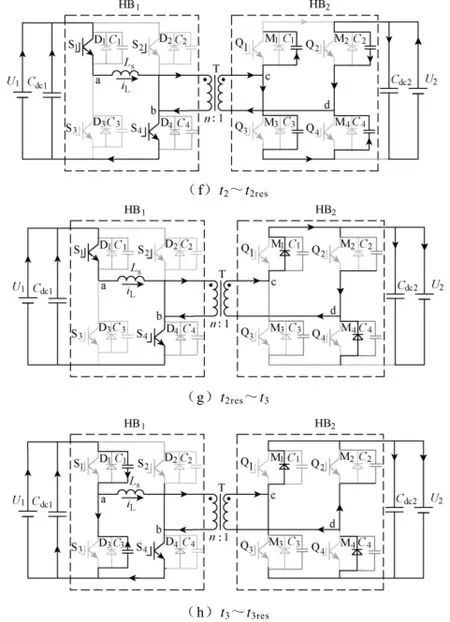
图2 双重移相控制下变换器工作模式Fig.2 Operation states of DAB DC-DC converter by Dual-Phase-Shifting control strategy

然而滞后臂发生开关动作时，一次侧电流更接近于零，因而更不容易实现软开关。由式（5）可知，为保证uC4(t)的电压能谐振下降到零，应满足:VCM2≥U1+nU2，整理可得滞后臂开关管零电压开通条件

uC4(t)的电压在t1res时刻谐振下降为零，此时一次侧电流可表示为

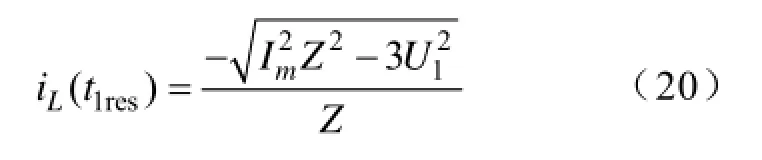
2.3.2 高频变压器二次侧H桥软开关实现

与一次侧H桥不同的是高频变压器二次侧H桥两个桥臂之间的触发信号没有移相，且t1与t4时刻发生开关动作时电路运行状态正负对称。由式（9）可知:VCM3≥nU2-12Un，因而电感储能足以使snubber电容谐振放电完成。

2.3.3 死区设定

根据式（2）可求得超前臂谐振放电时间为

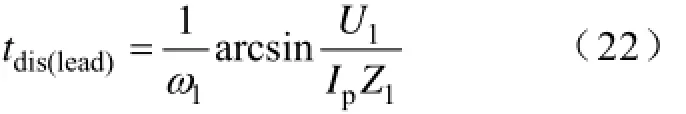
根据式（22）可知，只要使超前臂的导通与关断信号之间的死区时间Δτlead＞tdis(lead)，则满足超前臂开关管零电压开通条件并且保证超前臂不会直通短路。根据式（5）可求得滞后臂谐振放电时间为

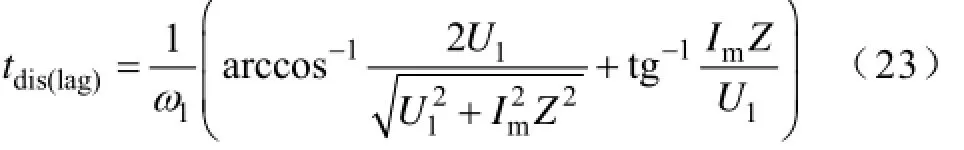
根据式（23）可知，只要使滞后臂的导通与关断信号之间的死区时间Δτlag＞tdis(lag)，则满足滞后臂开关管零电压开通条件并且保证超前臂不会直通短路。根据式（9）可求得变压器二次侧桥臂谐振放电时间为

根据式（24）可知，只要使二次侧H桥开关管的导通与关断信号之间的死区时间Δτsec＞tdis(sec)，则满足滞后臂开关管零电压开通条件并且保证超前臂不会直通短路。

超前臂开关管关断时电流大，放电时间短，死区时间短；滞后臂则相反；然而死区时间设置过长会造成损耗增大，因而死区设置时超前臂、滞后臂与二次侧H桥三个死区时间不同；但是工程实践中为方便操作，一般只设有一个死区时间，这时应以式（23）作为变换器死区时间设置的参考。

2.4内移相角与外移相角关系

图2c所示为0≤D1≤D2≤1时双重移相控制下双向直流变换器的理想工作波形，D1为变压器一次侧H桥的内移相比，D1∈[0,1]；D2为变压器二次侧H桥相对于一次侧H桥的外移相比:D2＞0.5时，能量由HB1传输至HB2，D2＜0.5时，能量由HB2传输至HB1。不考虑软开关谐振过程的情况下分析双重移相控制的软开关区域:U1=U2时，保证滞后臂开关动作时iL(t1)＜0，变压器二次侧H桥开关动作时iL(t1)＞0，可求得软开关区域为

然而iL(t1)＜0的条件并不能够保证完全实现软开关，因而3D1＜2D2是实现软开关的充分条件。根据式（2）、式（3）可知，在谐振放电过程中一次侧电流持续减小，则应满足

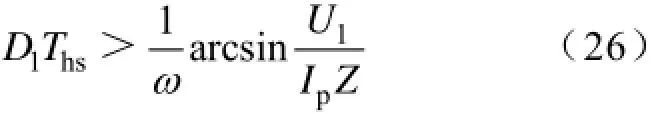
根据式（6）、（7）得出:t2-t1′=IqLSU1+nU2，因而满足（D2-D1）Ths＞（t2-）+tdis(lag)则可实现软开关，整理后可得满足软开关条件的移相比与变压器硬件参数关系

可见，基于上述分析，在变换器控制时应对移相角进行一定的限制。

3 漏感传输功率分析

根据表1列出的双重移相控制下双有源桥DCDC变换器能量传输状态，t1=Ths时刻将一个控制周期平分为电路状态对称的两个半周期，在每个半周期漏感的能量应守恒。

iL(t0)=-Ip，iL(t1)=-Im，则t1～t1阶段，漏感传输至U2侧功率为:p01-sec=LS(-)2。t1～t1res与t1res～1t′两个阶段，漏感同时向U1与U2传输功率，然而由于两个阶段电路运行状态不同，漏感向两侧传输功率的比例也不相同。t1～t1res阶段，U1与C4的串联支路与C1并联，同主回路的LS和二次侧等效电压源nU2形成谐振电路，谐振过程中C4与C1的互换，要求，因而U1与C4串联支路电流iC4为电感电流的一半，即iC4=iL2，则U1=nU2情况下代入式（20）可求得t1～t1res阶段漏感传输至两侧功率关系为

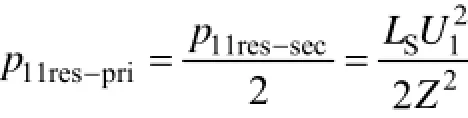
t1res～1t′阶段，U1，LS与二次侧等效电压源nU2组成串联回路对两侧传输功率为

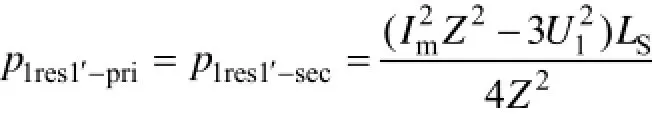
根据式（9），变压器二次侧H桥谐振结束时一次侧电流可表示为:则t2～t2res阶段U1向漏感储能:

U1=nU2情况下，iL(t)=iL(t2res)=Ip，漏感能量不变，即在前半周期内，漏感释放能量与U1、U2传输至漏感能量守恒，化简可得:回流功率即功率由U1侧传向U2侧过程中，t1～t1res与t1res～t1′阶段反向传输回U1侧功率，根据以上对单位控制周期内漏感能量分析可知回流功率可表示为

双向直流变换器作为高频隔离双向多电平变换器中间级，在运行过程中两侧直流电压保持不变，因而在功率维持恒定的情况下，漏感值越小，回流功率越小。

4 实验结果及分析

为了验证以上对软开关条件下，双有源桥直流变换器参数分析的正确性，根据上文理论推导得出的参数设计限制条件，设计了双有源桥DC-DC变换器实验平台，其中高频变压器串联电感为40μH。并测试了串联电感分别为200μH与40μH情况下，双重移相控制的双有源桥DC-DC变换器的效率。高频变压器与串联电感详细设计参数见表2。

表2 高频变压器与串联电感参数Tab.3 The parameter of high-frequency transformer and inductor of bidirectional DC-DC converter

图3为电感为40μH，开关频率20kHz，额定功率150W，改进的双重移相控制下运行时，双有源桥DC-DC变换器的电压与电流波形图。图3a中电感电流波形与图1c理想状态基本一致；由于并联snubber电容与串联电感组成的谐振电路，电压发生变化时，电压冲击较小；图3b为电感电流过零瞬间的展开图，滞后臂开关动作结束时电感电流小于零，满足软开关条件。

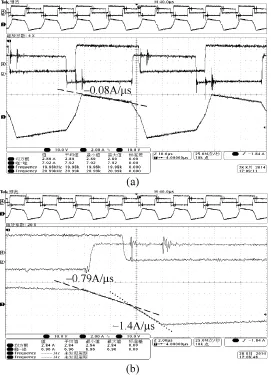
图3 双重移相控制下双有源桥DC-DC运行波形图Fig.3 Waveforms of DAB DC-DC converter controlled by DPS

图4 所示为采用200μH和通过上文所述电感优化方法计算得到的40μH电感的双向DC-DC变换器的效率、损耗与输出功率间的关系图。其中η1和PLOSS1为200μH电感下的效率和损耗，η2和PLOSS2为40μH电感下的效率和损耗。由图知，优化取值后的电感可使双向DC-DC变换器效率达到约96.8%，在系统输出功率较大的情况下，较之优化电感前系统效率有了明显提升，同时减少了损耗。

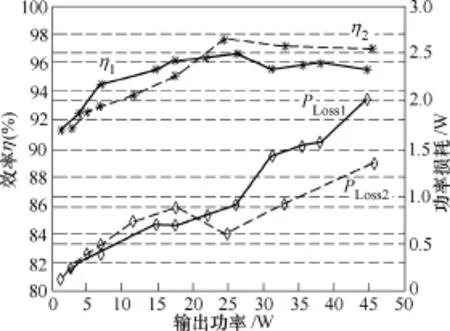
图4 不同串联电感量下直流变换器效率比较Fig.4 Comparison of efficiency of DAB DC-DC converter between different values of inductor

5 结论

本文对双重移相控制下双有源桥DC-DC变换器的软开关过程与实现条件、漏感与串联电感的能量的变化特点与回流功率进行了分析，在此基础上提出通过优化设计电路参数与合理设定死区时间结合的方式，保证直流变换器实现零电压开通与关断，降低开关损耗从而提升变换器效率。理论分析与实验结果表明，本文所提出的设计方法与改进的控制器可以保证软开关的实现，降低系统损耗，提高变换器效率。

[1] Shigenori Inoue, Hirofumi Akagi. A bidirectional isolated DC-DC converter as a core circuit of the next-generation medium-voltage power conversion system[J]. IEEE Transactions on Power Electronics, 2007, 22(2)： 535-542.

[2] HQS Dang, Alan Watson, Jon Clare, et al. Advanced integration of multilevel converters into power system [J]. IEEE IECON, 2008： 3188-3194.

[3] Alex Q Huang, Mariesa L Crow, Gerald Thomas Heydt, et al. The future renewable electrical energy delivery and management (FREEDM) system： the energy internet [J]. Proceedings of the IEEE, 2011, 99： 133-148.

[4] Kheraluwala M H, DeDoncker R W, Divan D M. Performance characterization of a high-power dual active bridge dc-to-dc converter[J]. IEEE Transactions on Power Electronics, 1992, 28(6).

[5] Demetriades G D, Hans Peter Nee, Hung. Dynamic modeling of the dual-active bridge topology for highpower applications[C]. IEEE Power Electronics Specialists Conference, 2008： 457-464.

[6] Xu Dehong, Zhao Chuanhong, Fan Haifeng. A PWM plus phase-shift control bidirectional DC-DC converter [J]. IEEE Transactions on Power Electronics, 2004, (3)： 666-675.

[7] Jing Penghui, Wang Cong, Jiang Wei, et al. Performance analysis of isolated three-level half-bridge bidirectional DC/DC converter[C]. Proceedings of IEEE 7th International Power Electronics and Motion Control Conference, 2012, 3： 1527-1531.

[8] Bai H, Mi C. Eliminate reactive power and increase system efficiency of isolated bidirectional dualactive-bridge DC-DC converters using novel dualphase-shift control[J]. IEEE Transactions on Power Electronics, 2008, 23(6)： 2905-2914.

[9] Zhao Biao, Yu Qingguang, Leng Zhiwei, et al. Bidirectional full-bridge DC-DC converters with dualphase-shifting control and its backflow power characteristic analysis[J]. Proceedings of the Chinese Society of Electrical Engineering, 2012, 32(12)： 43-50.

[10] 程红, 高巧梅, 等. 基于双重移相控制的双有源桥DC-DC变换器动态建模与最小回流功率控制[J].电工技术学报, 2014, 29(3)： 245-253.

Cheng Hong, Gao Qiaomei, et al. Dynamic modeling and minimum backflow power controlling of the bi-directional full-bridge DC-DC converters based on dual-phase-shifting control[J]. Transactions of China Electrotechnical Society, 2014, 29(3)： 245-253.

[11] Wang Y C, Wu Y C, Lee T L. Design and implementation of a bidirectional isolated dual-ac

tive- bridge-based DC/DC converter with dual-phase-shift control for electric vehicle battery[C]. IEEE Energy Conversion Congress and Exposition (ECCE), 2013：5468-5475.

[12] Kim M, Rosekeit M, Sul S K, et al. A dual-phase-shift control strategy for dual-active-bridge DC-DC converter in wide voltage range[C]. IEEE 8th International Conference onPower Electronics and ECCE Asia (ICPE & ECCE), 2011： 364-371.

[13] Biao Z, Song Q, Liu W. Power characterization of isolated bidirectional dual-active-bridge DC-DC converter with dual-phase-shift control[J]. IEEE Trans. Power Electron. , to be published.

[14] Bai H, Mi C C, Gargies S. The short-time-scale transient processes in high-voltage and high-power isolated bidirectional DC-DC converters[J]. IEEE Transactions on Power Electronics, 2008, 23(6)：2648-2656.

[15] Peng F Z, Li H, Su G J, et al. A new ZVS bidirectional DC-DC converter for fuel cell and battery application[J]. IEEE Transactions on Power Electronics, 2004, 19(1)： 54-65.

[16] 王聪. 一种简单的 ZVZCS 全桥 PWM 变换器的分析与设计[J]. 电工技术学报, 2000, 15(6)： 35-39.

Cong Wong. Analysis and design of a zero-voltage zero-current-switching full-bridge PWM converter with simple typology[J]. Transactions of China Electrotechnical Society, 2000, 15(6)： 35-39.

The Analysis of Zero Voltage Switching Dual Active Bridge DC-DC Converters Based on Dual-Phase-Shifting Control

Wang Cong Sha Guanglin Wang Jun Zhuang Yuan Cheng Hong
（China University of Mining & Technology(Beijing) Beijing 100083 China）

The soft-switching conditions and the operation stages of dual active bridge DC-DC converter are analyzed. Optimized parameters of DAB converter are proposed which meet requirements of zero-voltage-switching under the control of dual-phase-shifting. The method of combining optimized parameters with limited dead time is proposed to reduce switching power dissipation and raise efficiency based on analysis of mathematical model of each steady-state operation. At last, the effectiveness of optimization of parameters are validated by experiments based on an experimental prototype, and experimental results also verify the effectiveness of the points proposed in the paper.

Dual-active-bridge DC-DC converter, dual-phase-shifting control, zero-voltageswitching, dead time, efficiency

TM46

王 聪 男，1955年生，教授，博士生导师，研究方向电力电子与电力传动。

国家自然科学基金重点资助项目（51077125）。

2014-09-10

沙广林 男，1988年生，博士研究生，研究方向为大功率级联式电力电子变换器。（通信作者）