浅谈数形结合的高中数学解题策略

何红兵

（福建省南平一中）

数形结合在数学解题中应用，要特别意识到数与形两者之间相互表征的学习和锻炼：数形结合主要彰显数与形的相互转化，通过二者的相互表征和转化，能形象转化数学解题的“互译”。尤其当数学问题以代数形式或者与几何题型结合时，学生在解题过程中，应有效利用图形将问题转化成图形，使复杂的数学问题得以形象展现，即借助图形直观挖掘数学的几何意义。这样不仅有助于学生对数学问题的深层次理解，还能体现学生学习数学的灵活性和对知识的活学活用。

一、数形结合的数学思想

我国著名数学家华罗庚曾经说过：“数缺形时少直观，形缺数时难入微。”数形结合赋予了数学生命力，让数学问题的条件和结论同时展现其代数意义，又揭示其几何直观效果，让数学问题可以借助简单的图形、符号和文字所作的示意图，促进学生形象思维和抽象思维的协调发展，沟通数学知识之间的联系，从复杂的数量关系中凸显最本质的特征。

之所以说数形结合是一种重要的思想方法，是因为其在数学解题中的广泛应用。数形结合是一种重要的数学思想和一柄双刃的解题利剑。这是数形结合在解题方法基础上的一种提升，是目前高中数学教学中正在被接受的一种认识。它不再被看成是一种解题工具，而被看成是站在更高角度上用于指导解题教学，甚至是数学教学的一种思想策略。

数形结合既是一种解题方法，也是一种数学意识，在解题过程中有着十分广泛的应用。数形结合是一种数学思想，是一个值得认可的观点。但数形结合可以从数学思想上升为一种数学意识，甚至是一种意识。作为一种数学意识，时刻活动在数学教与学中，所发挥的数学教育意义会更大；作为一种意识，活动在生活的方方面面，发挥的作用会更大，影响会更广，这样它的教育价值也就更大。

二、高中数学中数形结合的解题策略

运用数形结合可以求解大量问题，但是在数学题型中，每类问题都各有特点，每一类问题都有一定的特点。以下就各类问题特征谈论一下运用数形结合的解题策略：

1.适用性

在对高中数学问题的梳理中，可以具体分为以下几类：（1）与函数相关的问题，通过图象及其性质来找到函数问题的突破口；（2）在求解方程和不等式问题中的运用；（3）在附属问题上，经常用到几何图形来求解；（4）求最大值或者最小值的问题，这类问题通过对图形与数量之间的特殊关系分析，使得问题更加直观，求解简便快捷。

2.广泛性

数与形的转换在高中数学中的应用十分广泛，通过数形转化，可以借助于图象研究函数的性质求函数的解析式、定义域、值城，极值与最值；还可以通过数形转化来研究函数的奇偶性、增减性、周期性；比较大小；判断和证明不等式以及解方程等。不仅如此，数形转化在复数、三角、解析几何中的应用也十分普遍。

3.以形促数

以形助数、以数辅形。这类方法通常用于代数式的几何意义或借助函数的图象构造几何图形入手，例如数形结合思想在不等式证明中的几点应用：（1）结合平面图形，运用勾股定理和三角形三边的关系来证明不等式；（2）结合平面图形，通过面积的不等关系来证明不等式；（3）通过利用圆中直径与弦的关系和其他圆的知识，证明不等式等等。

另外，在运用数形结合思想解题时，有些问题较明显，但有些问题需要通过几何图形来形象展示，比如：（1）过构造几何模型；（2）三角函数中常用的构造方法：构造直角三角形、构造相似三角形、构造单位圆、构造圆锥曲线方程。

综上所述，能用数形结合求解的问题很多。通过数形结合解题在高中数学各知识层面中都比较常见，大致总结其常用如下：（1）在求解集合题的过程中，经常是将文字和数轴相结合来进行；（2）在求解函数问题过程中的应用，包括三角函数求解，可以求函数的解析式、定义域、值城、极值与最值，也可以研究函数的奇偶性、增减性、周期性，还比较函数的大小，这些都是结合函数的图象性质进行的；（3）在求解向量问题中的应用，要充分联系向量的几何意义；（4）在求解不等式问题中的应用，可以通过函数特点或者构造几何图形来求解；（5）在求解解析几何问题中的应用，通常需要建模方法加以辅助等。

三、数形结合的解题实例分析

数形结合的解题过程：审题后联想到距离公式，将所求的函数做如下转化：

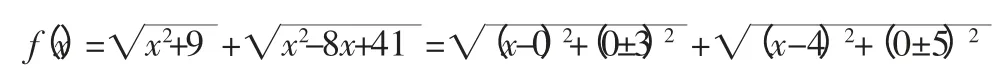
求解的函数图形

在高中数学中，数形结合的思想更多的是作为众多研究的思维方法和手段中的一种存在，可以简单地理解为有些数学问题是难以用直观的图示来表达的。尽管如此，数形结合的方法依旧对高中数学解题乃至整个高中数学教学有着重要的作用。高中数学解题中常用的方法有数形结合、整体性、分类讨论、类比联想、逆向思维、化归转化和构造性七种思想方法。数学思想与数学方法是数学知识的核心和灵魂。数形结合的思想在高中数学中占有举足轻重的地位。高中数学的很多题目都需要根据题目条件画出图形，因为通过图形能够很直观地看出各种关系。学习数学要勤思考，多总结，把数学的思想和方法灵活地运用到解题中去，才能发现数学学科的趣味和奥妙！

［1］李亚湖.数形结合在高中数学中的应用［J］.广东教育：教研版，2011（06）：132.

［2］赵红英.数形结合思想在解题中应用点滴［J］.中国科教创新导刊，2013（18）：205.