透过现象看本质抽丝剥茧现原形

☉浙江省宁波市镇海区骆驼中学 刘 红

透过现象看本质抽丝剥茧现原形

☉浙江省宁波市镇海区骆驼中学 刘 红

从近几年的中考题和模拟考试题来看，某些有一定难度的数学题经过变化引申、层层“伪装”，看似与圆无关，如果我们能深入挖掘题目中的隐含条件，或整体观察，或抽丝剥茧，或分解转化，善于联想所学定理，巧妙地让其现出符合题意特征的“原”形，往往能促使问题转化，使问题中原来隐晦不清的关系和性质在圆中清晰地展现出来，从而起到化隐为显、化难为易的解题效果.

一、定点定长现“原”形，借力圆形觅通法

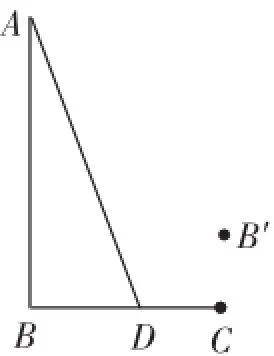
图1

解析：首先利用三角函数即可求得∠BAC=30°，当点D由点B位置向右运动至点C位置时，相应的点B′所经过的路径是以A为圆心，以AB为半径，圆心角是60°的弧，利用弧长公式即可解得相应的点B′所经过的路程是

评注：本题是一道单动点和折叠问题，主要考查特殊角的三角函数值、三角形边角关系以及弧长的计算、轴对称的性质，此题抓住轴对称图形的性质（如果两个图形关于某直线对称，那么对称轴是任何一对对应点所连线段的垂直平分线），推知点B′所经过的路径是以A为圆心，以AB为半径，圆心角是60°的弧是关键.

例2如图2，正方形ABCD，已知AB=8，动点P、Q在正方形ABCD的边上运动，且PQ=8.若点P从点A出发，沿A→B→C→D的线路，向点D运动，求点P从点A到点D的运动过程中，PQ的中点O所经过的路径的长.

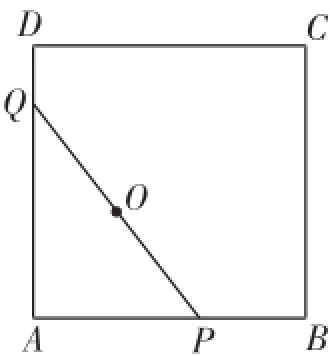
图2

解析：当点P从点A出发，沿A→B→C→D的线路，向点D运动时，不妨设点Q在DA边上，若点P在点A，点Q在点D，此时PQ的中点O即为DA边的中点；若点Q在DA边上，且不在点D，则点P在AB上，且不在点A.此时，在Rt△APQ中，O为PQ的中点，所以AO=PQ=4.所以点O在以A为圆心，半径为4，圆心角为90°的圆弧上.PQ的中点O所经过的路径是三段半径为4，圆心角为90°的圆弧，如图3所示.所以PQ的中点O所经过的路径的长为3×2π=6π.

图3

评注：本题涉及点的运动轨迹，解题难点在于分析动点的运动轨迹，需要很好的空间想象能力和作图分析能力，此题抓住直角三角形的性质（直角三角形斜边上的中线等于斜边的一半）推知PQ的中点O所经过的路径是三段半径为4，圆心角为90°的圆弧是关键.

例3如图4，在边长为2的菱形ABCD中，∠A=60°，M是AD边的中点，N是AB边上一动点，将△AMN沿MN所在的直线翻折得到△A′MN，连接A′C，则A′C长度的最小值是_________.

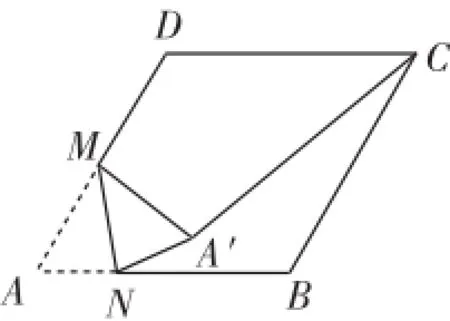
图4

解析：因为M是AD边的中点，A′M=AM=1，所以点A′在以M为圆心，1为半径的圆上，因此连接CM，当点A′落在CM上时，A′C长度的最小.过M点作MH⊥CD交CD的延长线于点H，则由已知可得，在Rt△DHM中，DM=1，∠HDM=60°，所以

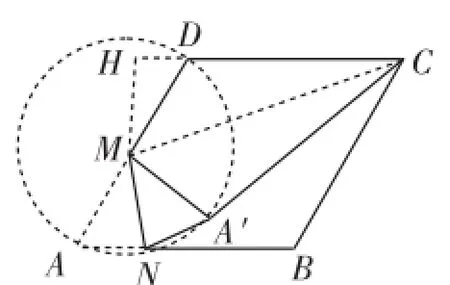
图5

评注：本题主要考查菱形的性质及锐角三角函数等知识，本解法简单，思路清晰，但对学生数形分析与转化能力的要求较高，需要充分利用轴对称性进行研究和分析.此题抓住A′M=AM=1推知点A′在以M为圆心，1为半径的圆上，要使A′C长度的最小即要∠CMA′最小，此时点A′落在NC上是关键，并将“两点之间线段最短”这一原理渗透在具体问题的解决过程中.

二、定线定角现“原”形，细究圆形探联系

例4如图6，B是线段AC的中点，过点C的直线l与AC成60°的角，在直线l上取一点P，使得∠APB=30°，则满足条件的点P的个数是（）.

A.3个B.2个

C.1个D.不存在

图6

解析：要在直线l上找点P使∠APB=30°，可以构造以AB为边的等边三角形ABO，则∠AOB= 60°，然后以O为圆心，AB为半径，作⊙O，如图7，因为△ABO为等边三角形，所以OB∥l，所以点O到l的距离d＜r，所以⊙O与直线l有两个交点，P1、P2.因为∠AOB=60°，所以∠AP1B=30°，∠AP2B=30°，所以满足条件的点P的个数是两个，分别为P1、P2，所以选B.

图7

评注：本题主要考查了图形的运动和三角形有关知识，是一个融探究、推理、计算于一体的综合性试题.在动点的变化过程中探究直线l上满足∠APB=30°的点P，由圆周角定理“一条弧所对的圆周角等于它所对的圆心角的一半”或其推论“同弧所对的圆周角都相等”把问题转化构造圆及直线与圆的位置关系问题.本题体现了数形结合、转化化归的数学思想，构造辅助圆，交点立显现，很好地考查学生分析问题、解决问题的能力.

图8

例5如图8，在正方形ABCD中，动点E、F分别从D、C两点同时出发，以相同的速度在边DC，CB上移动.连接AE和DF交于点P，由于点E，F的移动，使得点P也随之运动，若AD=2，试求出线段CP的最小值.

解析：由于点E、F的移动速度相同，可得△EAD≌△FDC，所以∠EAD=∠FDC；因为∠FDC+∠FDA=90°，所以∠EAD+∠PDA=90°，因此点P在运动中保持∠APD=90°，所以点P的路径是一段以AD为直径的弧，如图9所示.设AD的中点为O，连接OC交弧于点P，此时CP的长度最小，再由勾股定理可得OC=，再求CP=-1.

评注：本题以正方形为背景，借助动点问题计算线段的最小值，主要考查全等三角形、勾股定理的应用及线段的和差运算，将“直径所对的圆周角是直角和两点之间线段最短”这一原理渗透在具体问题的解决过程中，本题中隐含的辅助圆，能在一定程度上考查学生构图的能力（添加辅助线）.

例6如图10，直线y=-x+3与x轴、y轴分别交于点A、B，与反比例函数的图像交于点P（2，1）.

（1）求该反比例函数的关系式.

（2）设PC⊥y轴于点C，点A关于y轴的对称点为A′.

图10

①求△A′BC的周长和sin∠BA′C的值；

图11

因为点M在x轴上，所以点M是⊙E与x轴的交点.

因为EG⊥BC，所以BG=GC=1，所以OG=2.

因为∠EHO=∠GOH=∠OGE=90°，

所以四边形OGEH是矩形，所以EH=OG=2，EG=OH.

因为1＜m＜2，所以EH＞EC，所以⊙E与x轴相离.

当m=2时，EH=EC，所以⊙E与x轴相切.

a.当切点在x轴的正半轴上时，如图12所示，所以点M与点H重合.

图12

当m＞2时，EH＜EC，所以⊙E与x轴相交.

c.当交点在x轴的正半轴上时，设交点为M、M′，连接EM，如图13所示.

图13

综上所述：当1＜m＜2时，满足要求的点M不存在；

评注：本题考查知识点多，代数与几何等知识相互渗透，综合性非常强，难度较大，涉及分类、转化、数形结合、数学建模等常用的数学思想，考查了学生创造性思维及操作、探究、分析问题等能力，可谓知识与能力齐驱，基本数学思想和基本活动经验联动.而第（2）问的②中由条件

几何动点问题的题型较多，综合性较强，图形具有不确定性，寻找解题的突破口是关键，这就需要学生能够仔细分析，抓住问题的本质，挖掘隐含条件和潜在信息，理性分析动点过程中所维系的不变条件，通过几何构建进行转化.综上所述，涉及“定点定长”问题和“定线定角”问题，可通过构造辅助圆让其现出“原”形，化动为静，对满足条件的动点准确地定位再解答，这也是解决此类题的切入点与通法.

1.汪宗兴.巧用辅助圆妙解中考题［J］.中学数学（下），2010（11）.

2.沈岳夫.善归类细分析悟通法促提高［J］.中国数学教育（初中版），2014（12）.H