双曲线为母体的阴影面积

☉江苏省高邮市南海初级中学 姜 志

双曲线为母体的阴影面积

☉江苏省高邮市南海初级中学 姜 志

近几年的中考中有关阴影面积的题目变得俏丽多姿，异彩纷呈，给凝重的中考带来了生机与活力，其中有一族以坐标系为基的阴影面积问题，凭借坐标系的自然环境，有机链接了函数的图像，演绎出了多姿多彩的阴影，给中考增添了妙趣.现采撷近几年有关双曲线的考题，作一赏析，供参考.

一、孤单一影

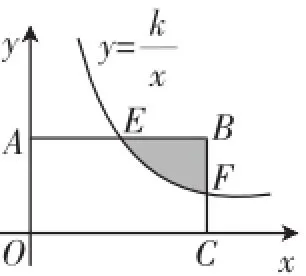
图1

解析：本题考查反比例函数的性质，正确表示出BF的长度是关键.设则B的纵坐标也为.由于E是AB的中点，所以F点的横坐标为2a.代入，得F的纵坐标，所以F也为BC的中点.

跟踪训练：（2014·湘潭市）如图2，A、B两点在双曲线上，分别经过A、B两点向轴作垂线段，已知S阴影=1，则S1+S2=（）.

A.3B.4C.5D.6参考答案：D

图2

二、相谐双影

例2（2010·深圳市）如图3，正比例函数与反比例函数的图像相交于A、B两点，分别以A、B两点为圆心，画与x轴相切的两个圆，若点A的坐标为（2，1），则图中两个阴影部分面积的和是_________.

图3

解析：用双曲线的中心对称性，两个阴影可拼成一个以A（或B）为圆心的整圆，因此，只要能确定其半径即可顺利完成.由于以A（2，1）为圆心的圆与x轴相切，则其半径为1，故答案为12π=π.

跟踪训练：（2011·贵州黔南州市）如图4，⊙A和⊙B都与x轴和y轴相切，圆心A和圆心B都在反比例函数的图像上，则图中阴影部分的面积等于_________.

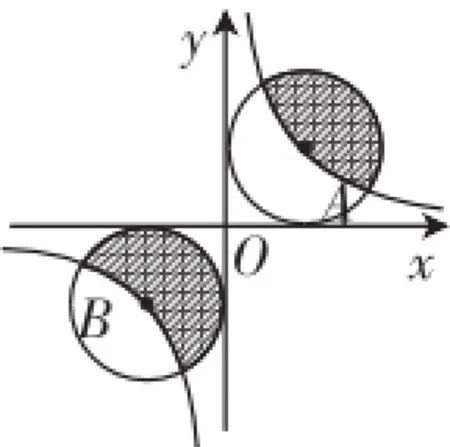
图4

参考答案：π

三、缤纷多影

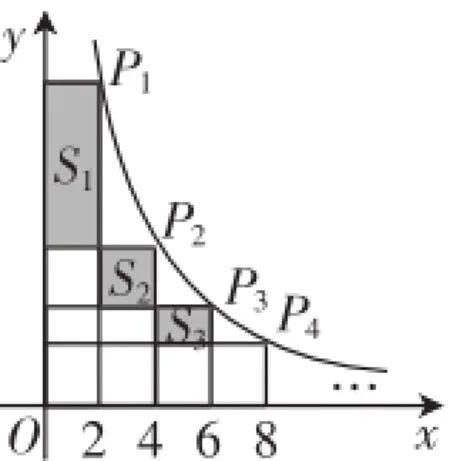
图5

解析：求出P1、P2、P3、P4、…的纵坐标，从而可计算出S1、S2、S3、S4、…的高，进而求出S1、S2、S3、S4、…，从而得出Sn的值.当x=2时，P1的纵坐标为4，当x=4时，P2的纵坐标为2，当x=6时，P3的纵坐标为，当x=8时，P4的纵坐标为1，当x=10时，P5的纵坐标为，….则S1=2×（4-2）=4=

跟踪训练：（2012·黑龙江）如图6，在x轴的正半轴上依次截取OA1= A1A2=A2A3=A3A4=A4A5=…，过A1、A2、A3、A4、A5、…分别作x轴的垂线与反比例函数的图像交于点P1、P2、 P3、P4、P5、…，并设△OA1P1、△A1A2P2、△A2A3P3、…的面积分别为S1、S2、S3、…，按此作法进行下去，则Sn的值为_________（n为正整数）.

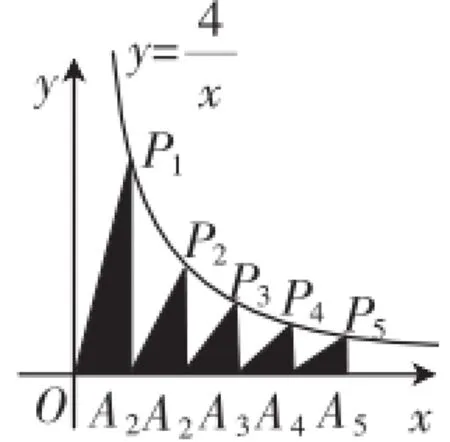
图6

通览以上可以发现，坐标系内神态各异的阴影图形，常考常新，经久不衰，成了中考的“常青藤”，其解法变化多端，但不管怎样，面积“阴影”以双曲线为载体，始终离不开反比例函数的图像和性质，因为反比例函数的比例系数与面积有着天然的联系，因此，熟练掌握反比例函数的图像及性质是破解此类问题不可或缺的武器.Z