四轮独立转向电动汽车转向控制方法*

马 雷，贡士娇，李 斌，汪 林，于 悦

(1.燕山大学车辆与能源学院，秦皇岛 066004； 2.交通运输部公路科学研究院智能交通技术交通行业重点实验室，北京 100088)



2015177

四轮独立转向电动汽车转向控制方法*

马 雷1，贡士娇1，李 斌2，汪 林2，于 悦1

(1.燕山大学车辆与能源学院，秦皇岛 066004； 2.交通运输部公路科学研究院智能交通技术交通行业重点实验室，北京 100088)

本文中对四轮独立转向电动汽车的转向控制方法进行研究。首先，基于前轮转向车辆的理想横摆角速度模型，建立四轮独立转向2自由度动力学模型。接着，以四轮侧偏角之和绝对值最小化作为优化目标函数，以质心侧偏角为零和理想横摆角速度作为约束条件，采用线型优化算法求解系统前馈控制器。再以轮胎侧偏角和横摆转矩为输入建立线性控制模型，运用最优区域极点配置方法设计反馈控制器。最后，建立人-车-路闭环仿真系统，分别进行双移线道路仿真实验和对开路面上的行驶仿真实验。结果表明，控制器能根据路面附着情况分配各轮转角，保证车辆跟踪理想状态。实车双移线实验进一步验证了控制器对车辆理想状态良好的跟踪精度。

四轮独立转向；前馈控制；区域极点配置；操纵稳定性

前言

操纵稳定性对汽车安全性有重要影响，四轮独立转向技术在低速时提高汽车的机动灵活性，在高速时改善汽车的操纵稳定性。国内外学者对于四轮独立转向进行了一些研究。文献[1]中利用自回正力矩和纵向力、侧向力之间的关系估计轮胎力裕量，使用序列二次规划法作为求解器进行控制分配，提出一种4WID-4WIS车辆动力学分层控制的方法。文献[2]中以车辆2自由度线性动力学模型为基础，假定车辆转向四轮符合阿克曼转向原理，设计了四轮独立转向前馈控制器，但其转向特性与四轮主动转向相仿。文献[3]中对4WID-4WIS车辆横摆稳定性控制进行了研究，对侧偏角和横摆角速度进行耦合性分析，利用模糊控制方法设计了控制器，但在建立动力性方程时没有考虑轮距，在中低速时与实际四轮独立转向车辆有差距，并且只设计了反馈控制器。文献[4]中针对4WID-4WIS电动车利用Matlab建立了整车动力学仿真模型，并验证仿真模型的正确性。文献[5]中提出了4WID-4WIS车辆路径跟踪控制方法，利用自抗扰控制方法设计路径跟踪系统纵向速度、侧向位移和横摆角速度3个动力学通道上的解耦控制器，并使用非线性规划方法进行控制器求解，但该方法需要轮胎纵向和横向滑移率的数据，不利于工程实际应用。另外，上述文献中的方法很难根据路面附着情况分配各转向轮转角，未充分发挥四轮独立转向在车辆稳定性方面的优势。

以四轮独立转向车辆为研究对象，建立四轮独立转向车辆2自由度动力学模型，以四轮侧偏角之和绝对值为最小值建立目标函数，保证系统控制能量最小；根据车辆匀速稳态工况特点，以质心侧偏角为零和理想横摆角速度为约束条件，运用优化理论求解系统前馈控制器，并分析了不同附着路面控制器求解情况。以轮胎侧偏角和横摆转矩为输入建立系统线性控制模型，运用最优圆形区域极点配置方法设计反馈控制器，提高系统的动态响应能力，减小因模型摄动导致的系统静差。建立人-车-路闭环仿真系统，选取双移线道路模型进行模拟道路实验。进行了对开路面上仿真实验，验证了控制器可根据路面附着情况分配各轮转角，利用路面附着条件，保证车辆跟踪理想状态。采用双移线进行低速跟踪实车实验。实验表明，控制器对于车辆理想状态具有良好的跟踪精度，对模型摄动有较好的鲁棒性。

1 车辆理想横摆角速度的获取

理想四轮独立转向控制应使车辆横摆角速度增益与前轮转向汽车保持一致，保证驾驶员驾驶感觉不发生很大变化。因此以前轮转向车辆2自由度动力学模型为基础，计算车辆理想横摆角速度。理想横摆角速度有两方面作用：一是在前馈控制器设计时将其作为一个约束条件；二是反馈控制时作为理想状态。在转角低频输入车辆稳态响应的情况下横摆角速度与转角可以简化为1阶环节[6]：

(1)

式中：γ*为理想横摆角速度；Gr为稳定性因素；Tr为横摆角速度延迟时间常数；δ为驾驶员输入前轮转角；uc为车速；m为整车质量；a和b为车辆质心至前后轴距离；Iz为车辆绕垂直轴的转动惯量；kf和kr为前后轮侧偏刚度；L为轴距。

2 控制器设计

2.1 车辆控制模型的建立

以课题组研发的四轮独立转向电动车为研究对象。底盘总成由转向系统、悬架系统和制动系统组成。电气总成由电源系统、驱动控制系统、转向控制系统、测控系统和控制台等5个部分组成。车辆2自由度动力学方程为

(2)

式中：下标1～4为车轮序号，分别对应左前轮、右前轮、左后轮、右后轮；αi为四轮侧偏角；ki为轮胎侧偏刚度；β为质心侧偏角；γ为横摆角速度；M为横摆力矩，M=(c/2)(Fx1-Fx2+Fx3-Fx4)，Fxi为车轮纵向力。

各轮侧偏角为

(3)

式中：v为车辆侧向速度；δi为四轮转角；c为轮距。

图1为四轮独立转向控制系统框图，驾驶员输入转角经参考模型得到γ*，通过前馈和反馈控制器作用于车辆实现转向控制。

2.2 前馈控制器设计

2.2.1 性能指标函数选取

前馈控制器是整个控制方法的核心，根据最优控制理论，控制器设计时应考虑整个过程中实际状态偏离期望状态的程度和整个过程中所消耗的能量。因此以系统消耗能量最小建立性能指标函数，以系统状态作为约束条件，利用线性优化方法求解前馈控制器。性能指标函数为

minJ=|α1+α2+α3+α4|

(4)

根据车辆动力学，γ与各转向轮轮胎侧偏角符号相反，即与αi方向相同，因此选取车辆各轮侧偏角之和的绝对值作为系统性能指标函数。由于αi为式(2)控制模型中的输入，式(4)为最小值可保证系统控制消耗能量最少。

2.2.2 约束条件选取

(5)

以式(4)为性能指标函数，将式(5)作为约束条件。将优化解中αi代入式(3)，令v=0，可保证β=0，同时求解δi。由于β和γ为式(2)车辆模型中的系统状态，把系统状态作为前馈控制器约束条件，可保证在系统控制能耗最小的前提下，既保证车辆转向时β为零，又使γ能很好地跟踪γ*。

横摆力矩M是式(2)中的控制输入，将其作为约束条件主要是由于M和αi量纲不同，性能指标函数不包含M项可不用考虑二者之间的权重关系，有利于性能指标函数建立。同时利用线性优化方法求解式(4)时可直接获得αi和M优化解。

2.2.3 前馈控制器仿真分析

根据实验车情况，选取m=495kg，I=365kg/m2，a=0.798m，b=0.891m，ki=-20(kN/rad)，c=0.5m。图2为γ*=0.3rad/s，uc由1至30m/s时δi和M变化曲线；图3为uc=15m/s，γ*由0.1至0.4rad/s时δi和M变化曲线。

由图2可见，车速较低时前后轮转动方向相反，车速较高时前后轮转动方向相同，符合四轮转向特点，即满足车辆在低速时的灵活性和高速时的稳定性。由图3可见，随着γ*变大，各转向轮转角变大，符合车辆转向特点。在图2和图3中M优化解基本为零，说明四轮独立转向车辆可通过控制转角使车辆动力学状态置于理想状态。由于四轮独立驱动汽车可通过改变各轮的纵向力FXi降低车辆行驶时车轮的附着率，减小轮胎的滑移率，改善轮胎附着情况[7]，因此在车辆转弯工况时可根据各轮驱动力分配结果计算M，并将其作为式(5)中的一个约束条件，对前馈控制器求解，既可提高车辆横向操纵稳定性，又能改善纵向附着情况。

根据汽车理论，随着轮胎侧偏角变大，车轮侧向力从线性增加逐步过渡为非线性增加，最终趋近于饱和，轮胎侧偏角不超过5°时，轮胎侧向力与侧偏角呈线性关系。由于附着系数不同的路面轮胎所能提供侧向力大小也不同，同时轮胎纵向力和侧向力受附着椭圆约束，因此在对开路面等工况下，当附着系数低的一侧轮胎进入非线性区时，可通过增大附着系数高的一侧轮胎转角保持车辆行驶的稳定性。假设车辆行驶在对开路面上，左侧为干沥青路面，其附着系数为0.9，右侧为湿沥青路面，其附着系数为0.6，左右两侧线性区最大侧偏角分别为±0.09rad和±0.06rad。uc=30m/s和γ*=0.3rad/s时，将最大侧偏角作为式(5)一个约束条件，前馈控制器解和δi如表1所示。图4为车辆状态收敛图。

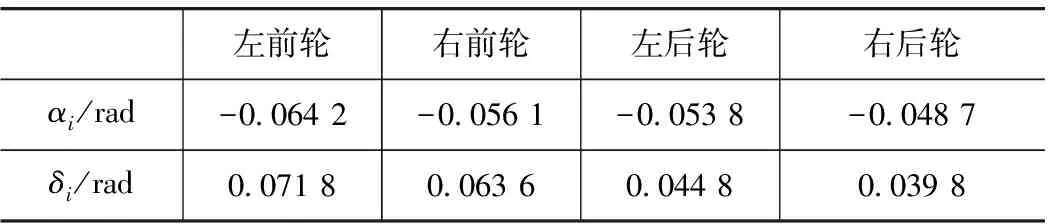
表1 各轮侧偏角和转角

从表1可以看出，车辆右侧各轮转角明显小于左侧，说明前馈控制器可根据路面附着情况分配各轮转角，充分利用路面附着条件。由图4可见，车辆状态γ最终收敛于0.3rad/s，β收敛于零，在前馈控制器作用下车辆处于理想状态。

图5为车辆初始状态uc=30m/s,β=0，γ=0时，γ*=0.3rad/s，在前馈控制器作用下系统收敛曲线。

由图5可见，系统状态γ在0.6s达到峰值，在模型无摄动工况下系统状态收敛于理想值，即β=0，γ=0.3rad/s；在模型有摄动工况下系统状态虽然收敛于理想状态附近，但还是存在静差。从图5可看出前馈控制器存在两点不足：一是车辆β和γ进入稳态的时间较长，同时存在超调；二是在模型存在摄动时γ与γ*存在明显静差。因此须通过反馈控制器提高系统响应速度，减小超调和系统静差。

2.3 反馈控制器设计

如果将式(3)代入式(2)，以δi和M作为控制模型输入，模型为非线性模型，不利于控制器设计。根据式(2)，系统控制模型如式(6)所示。将控制器解代入式(3)得到转向轮转角。

(6)

Δu=[α1α2α3α4M]T

在前馈和反馈控制器共同作用下，系统的动态特性应与式(1)理想模型基本相同。图6为δ=0.1rad，uc为10，20和30m/s的阶跃响应曲线。图7为式(1)极点随uc由5至40m/s的变化曲线。

由图6可见，γ到达稳态时间在0.1s左右，车辆在前馈和反馈控制器作用下系统的响应速度应该与图6中γ的响应速度大体相当。由图7可见，当uc=15m/s时，式(1)的极点最大，响应速度最慢，车速较大和较小时其响应速度都会增加。根据自动控制原理，系统状态的瞬态响应能力与闭环极点位置有关，应使在反馈控制器作用下闭环系统的极点与式(1)相近，保证系统瞬态响应能力，因此反馈控制器应首先保证闭环系统极点位置。选用最优圆形区域极点配置方法设计反馈控制器，不但可以克服传统的极点配置方法不能很好地分配各状态与输入之间的权重，而且可保证闭环系统极点处于理想位置。选择半正定加权矩阵Q和正定加权矩阵R，令反馈控制器Δu=kx，使评价函数

(7)

s=(r(b+w))/(b-w)-a(a，r，b>0)

(8)

使S平面中圆形区域转换为W平面的左半平面[8]。

定理1[8-9]设A和B满足条件：(1)为可控对；(2)A在-(a+r)处无特征值。令

A1=b[(r+a)I+A]-1[A-(r-a)I]

B1=b[(r+a)I+A]-1B

B2=(bI-A)B1

则式(6)可变换为

(9)

存在反馈增益

k=(I-k1B1)-1k1

(10)

使系统闭环极点置于给定区域圆内，其中

其中P是代数Riccati方程

PA+ATP-PBR-1BTP+Q=0

的对称正定常数解。

系统控制器输出为

u=r+Δu

(11)

式中：r为参考输入，是2.2节设计的前馈控制器。

在设计最优圆形区域极点配置控制器时存在r，b，Q和R待定参数。通过仿真分析，b对控制器影响不大，此处选取b=2，令反馈增益k为

图8(a)～图8(c)为uc=30m/s，a=45，Q和R为单位对角阵时，r从1～44，反馈增益k、闭环极点变化曲线；图8(d)为r=1和44时系统收敛曲线。

由图8(a)和图8(b)可见，随r增大，与β相关反馈增益系数变小，与γ相关反馈增益系数变大。当r取较大值时，与β和γ相关的反馈增益系数大小趋向相近，有利于平衡β和γ之间的关系，而且图8(b)中前后轮对应的反馈增益系数绝对值大小趋向相近，有利于通过前后轮共同调节车辆状态，符合车辆转向实际情况。由图8(c)和图8(d)可见，随r增大，γ极点位置变化不大，β逐渐增大；当r为1和44时系统状态收敛情况大体相仿，只是在r=1时系统状态有微小超调。因此，r应选取较大值。

通过仿真实验，最终选取r=44，Q=diag(1，1)，R=diag(1，1，1.3，1.3，1)和a=45。选取模型摄动与图5条件相同，图9和图10分别为uc=5m/s和30m/s时系统收敛曲线。

从图9和图10可以看出，在前馈和反馈控制器共同作用下，系统动态响应速度得到了明显提高，与式(1)理想模型动态响应速度基本相同，为0.1s左右。虽然模型存在较大摄动，车速较低时车辆状态β和γ与理想状态基本吻合。与图5(b)对比，车速较高时在反馈控制器作用下，γ的静差明显减小，状态β和γ的超调得到较好的抑制。

3 道路仿真实验

在四轮独立转向汽车模型和控制器模型的基础上，依据预瞄最优曲率理论[10]，建立人-车-路闭环仿真模型，验证控制器品质。单点预瞄驾驶员模型中预瞄时间为0.82s，校正时间为1s，神经反应延迟时间为0.3s，操纵缓冲时间为0.1s。图11为采用双移线模型在uc=30m/s时的道路仿真实验结果，以验证控制器的跟踪性能。

由图11可见，在控制器作用下车辆较好地跟踪理想道路；由于车辆速度较高，使δ1与δ2差距很小，δ3与δ4情况相同；对于跟踪γ*理想效果较好。图12为γ*与γ差值图。从图中看出，跟踪最大偏差不超过0.01rad/s；β很小，几乎为零，说明控制器具有较好的跟踪性能。

为验证车辆在对开路面行驶情况，选取与图4相同道路条件和uc，令车辆跟踪γ*=0.3sin(πt)，图13为仿真结果。

从图13(a)和图13(b)看出，当|αi|接近0.06rad时，车辆前馈控制器根据约束条件自动分配四轮转角，保证右侧车轮侧偏角小于设定值。从图13(c)和图13(d)看出，β和γ较好跟踪了车辆理想状态，验证了控制器在对开路面等工况下的有效性。

4 实车实验

实验模型车4个车轮分别采用轮毂电机驱动，电机额定功率为2kW、额定转矩为45N·m、最高转速为650r/min。根据文中控制器的设计，车辆正常行驶时M几乎为零，因此实验时令M=0。车辆四轮驱动力分配采用等转矩策略，即4个轮毂电机输出电流相等，使电机输出转矩相同。采用VC 6.0开发环境下编译的四轮独立转向控制程序。由于实验模型车未安装转向机器人，故将仿真得出的双移线工况下驾驶员模型输出的车辆转角作为输入，并将其写入控制程序中。受到实验场地和车辆的制约，进行了低速实验验证。实验时，车速控制在大约5m/s的情况下，启动测试程序，测得横摆角速度和侧向加速度，进而得到质心侧偏角，并分别与理想值进行比较。图14为实验模型车现场图，图15为车辆状态跟踪图。

从图15看出，由于实验模型车转向系统动态响应速度的原因，使实车状态与理想状态存在一定的偏差，但车辆还是能较好地跟踪理想状态。

5 结论

(1) 建立以系统耗能为目标函数，以系统状态为约束条件设计前馈控制器。仿真实验表明，该前馈控制器能较好地跟踪车辆理想状态。该前馈控制器可根据路面附着情况分配各轮转角，充分利用路面附着条件，保证车辆跟踪理想状态。

(2) 利用最优圆形区域极点配置方法设计了反馈控制器。仿真实验表明，反馈控制器可提高系统的响应速度，抑制状态超调。在控制模型存在摄动的情况下，有利于减小状态静差。

(3) 前馈控制器和反馈控制器进行了仿真与道路实验，验证了控制器品质。

[1] Ono E, Hattori Y, Muragishi Y. Estimation of Tire Friction Circle and Vehicle Dynamics Integrated Control for Four-wheel Distributed Steering and Four-wheel Distributed Traction/braking Systems[J]. R&D Review of Toyota CRDL,2005,40(4):7-13.

[2] Chen Sizhong,Shu Jin,Yang Lin.Research on Vehicle Control Technology Using Four-Wheel Independent Steering System[J]. Journal of Beijing Institute of Technology,2006,15(1):22-26.

[3] 杨福广,阮久宏,李贻斌,等.4WID-4WIS车辆横摆运动AFS+ARS+DYC模糊控制[J].农业机械学报,2011,42(10):6-12.

[4] 宗长富,刘经文,郑宏宇,等.4WID/4WIS电动车建模和特殊工况仿真[J].汽车工程,2011,33(10):829-833.

[5] 阮久宏,杨福广,李贻斌.高速4WID-4WIS自主车路径跟踪控制[J].机器人,2011,33(4):411-418.

[6] 来飞,黄超群.汽车四轮转向变增益跟踪控制的研究[J].汽车工程,2012,34(6):517-522.

[7] Ossama Mokhiamar,Masato Abe. How the Four Wheels Should Share Forces in an Optimum Cooperative Chassis Control[J]. Control Engineering Practice,2006,14(3):295-304.

[8] Wittenmark B. Constrained Pole-placement Using Transformation and LQ-design[J]. Automatica,1987,23(6):767-769.

[9] 袁廷奇,刘文江.区域极点配置控制系统的鲁棒摄动界[J].西安交通大学学报,2000,34(7):99-102.

[10] 郭孔辉.汽车操纵动力学[M].长春:吉林科学技术出版社,1991:499-520.

Steering Control Scheme for Electric Vehicles with Four-wheel Independent Steering

Ma Lei1, Gong Shijiao1, Li Bin2, Wang Lin2& Yu Yue1

1.CollegeofVehicleandEnergy,YanshanUniversity,Qinhuangdao066004；2.KeyLaboratoryofTechnologyonIntelligentTransportationSystems,ResearchInstituteofHighway,MinistryofTransport,Beijing100088

The steering control method for electric vehicle with four-wheel independent steering (4WIS) is studied in this paper. Firstly based on the ideal yaw rate model for vehicle with front wheel steering, a 2 DOF 4WIS dynamics model is established. Then with minimizing the absolute value of the sum of four tire side-slip angles as optimization objective function and the zero side-slip angle of mass center and ideal yaw rate as constraints, the linear optimization problem is solved with the feed-forward controller of system obtained. Next, the linear control model is set up with tire side-slip angles and yaw torque as inputs and the feedback controller is designed by using the method of optimum region pole assignment. Finally, a driver-vehicle-road closed loop simulation system is established and both simulation experiments of double lane change and driving on μ-split road are conducted with a result showing that the controllers designed can properly distribute the steering angles of all wheels according to road adhesion conditions and thus ensure the vehicle follow ideal state, and the subsequent real vehicle double-lane change experiment further verifies the good tracking accuracy of controllers for vehicle ideal state.

4WIS; feed-forward control; region pole assignment; handling and stability

*教育部科学技术研究重点项目(211024)资助。

原稿收到日期为2014年1月13日，修改稿收到日期为2014年4月18日。