分布驱动式电动汽车电池系统分布形态对能耗特性影响的研究*

孙泽昌，曾英捷，戴海峰

(1.同济大学汽车学院，上海 201804； 2.同济大学新能源汽车工程中心，上海 201804)



2015182

分布驱动式电动汽车电池系统分布形态对能耗特性影响的研究*

孙泽昌1,2，曾英捷1,2，戴海峰1,2

(1.同济大学汽车学院，上海 201804； 2.同济大学新能源汽车工程中心，上海 201804)

针对分布式四轮驱动纯电动汽车，分析具有不同分布形态的电池系统能耗特性。选取Rint等效电路模型建立电池系统内阻损耗模型，通过理论计算分析分布式电池系统与集中式电池系统的能耗特性。然后基于AMESim/Simulink软件建立了电动汽车能耗特性仿真平台，并以驱动能量消耗最少为控制目标，对前后轴驱动电机转矩进行最优分配控制，在NEDC循环工况下对电池系统内阻损耗进行仿真。理论和仿真分析结果均表明：在分布式驱动情况下，采用集中式电池系统时的能耗特性优于分布式电池系统，且分布式电池系统会产生SOC不一致的问题，从而导致车载充电系统设计的复杂化。

电动汽车；分布式电池系统；集中式电池系统；能耗特性

前言

节能、环保和安全是现代汽车发展的三大主题，纯电动汽车在能源和环境方面符合可持续发展的要求，备受重视。

分布式驱动纯电动汽车是国内外研究的热点，其主要结构特征是将驱动电机分散布置到各个车轮[1]，结构紧凑，传动高效。动力电池系统作为纯电动汽车的储能部分，是电动汽车的关键部件，直接影响到电动汽车的性能[2]。

根据分布式驱动电动汽车的拓扑结构，电池系统的分布形态可分为集中式和分布式。集中式电池系统由单一系统组成，集中为驱动系统全部电机提供能量；分布式电池系统则由若干独立的电池子系统组成，分别为驱动系统中轴驱动电机或轮驱动电机提供能量。

对于分布式纯电动汽车，国内外大多研究集中于电机的拓扑结构及其转矩分配优化[2-4]，极少涉及为其供电的电池系统分布形态对分布式驱动性能的影响。然而，电池系统采用何种分布形态更有利于提高分布式驱动纯电动汽车的能量效率，这是分布式驱动电动车研究必须要回答的基本问题。本文中以实验测试数据为基础，通过理论推导和仿真分析，研究集中式电池系统和分布式电池系统用于分布式驱动的能耗特性。

1 电池系统损耗模型

1.1 电池系统分布形态

本文中针对四驱分布式驱动电动汽车，研究3种电池系统分布形态的能耗特性。对于纯电动汽车，由于其前轴载荷较大，为前轴所配置的电机功率通常都大于后轴电机。本文中选择四驱分布式驱动电动车前后轮电机参数如表1所示。

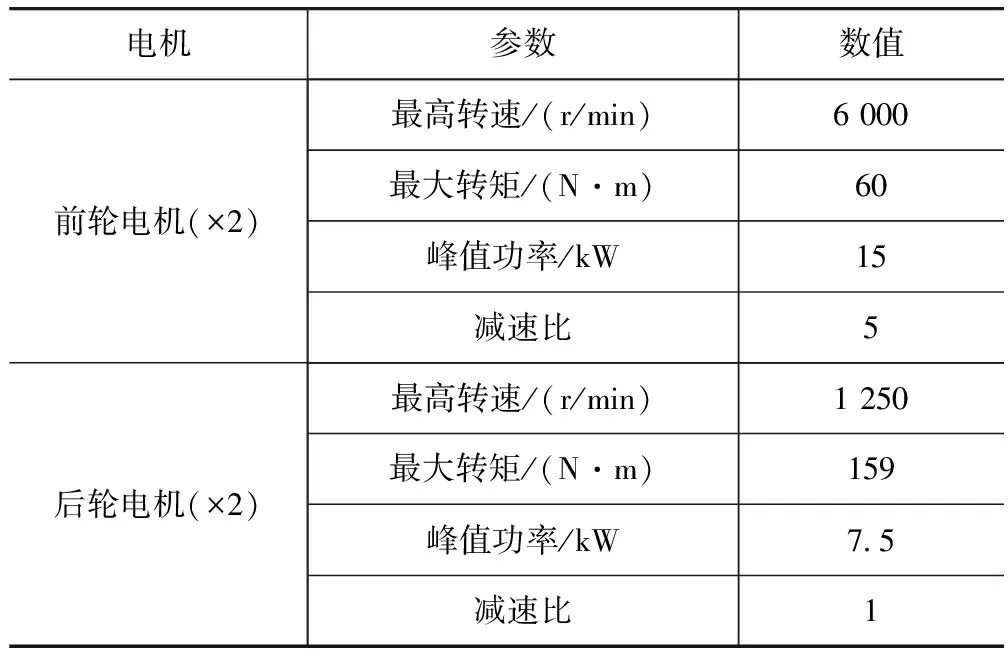
表1 电机参数

电池系统的容量与组成按照前后轮电机峰值功率的比例进行配置。设定一个电池组由N个单体电池串联而成，内阻为R，开路电压为E。电池分布形态如图1所示。

图1(a)为分布式电池系统A。2个前轮驱动电机分别由2个电池包Af为其供电，每个电池包Af由2个电池组并联而成；后轮电机由2个电池包Ar分别供电，每个电池包Ar由1个电池组组成。

图1(b)为分布式电池系统B。前轴2个轮驱动电机由1个电池包Bf为其供电，该电池包由4个电池组并联而成；后轴2个轮驱动电机由1个电池包Br为其供电，该电池包Br由2个电池组并联组成。

图1(c)为集中式电池系统，在该系统中只有1个由6个电池组并联而成的集中式电池包C同时为4个轮驱动电机供电。

令电池包Af，Ar，Bf，Br和C的内阻分别为RAf，RAr，RBf，RBr和RC，其开路电压分别为EAf，EAr，EBf，EBr和EC。假定各电池包初始SOC相同，其最大放电电流为4C，最大充电电流为3C，额定电压为320V，电池包容量参数如表2所示。

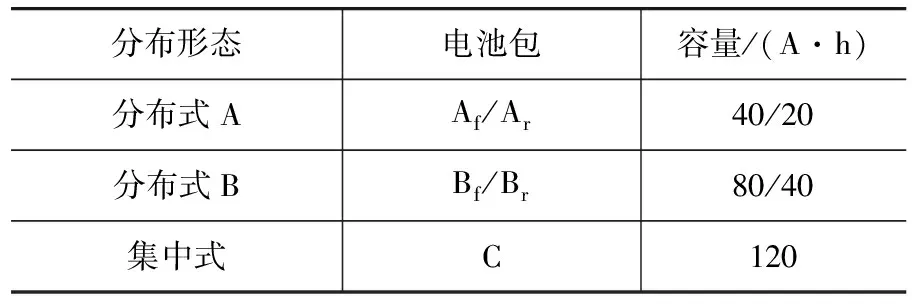
表2 电池包容量参数

1.2 电池等效电路模型

等效电路模型使用电阻、电容和恒压源等电路元件组成电路网络来模拟电池的动态特性，便于仿真分析和应用，在电动汽车仿真中应用最为广泛[5]。

典型的等效电路模型有Rint模型、RC模型、Thevenin模型和PNGV模型。由于本文中从电池系统分布形态的角度分析研究内阻损耗，所以选择Rint模型为单体电池等效电路模型进行分析。

Rint模型将电池等效为理想电压源E与电阻R的串联[6]，其表达式为

(1)

式中：U为电池端电压；I为电池电流；开路电压和内阻与SOC和温度T相关。

实验选用的对象为磷酸铁锂单体电池，额定容量为20A·h，电压工作范围为2.5～3.7V。在MACCOR-4300(USA)电池测试系统上对电池进行测试，测试过程如下：

(1) 将电池以恒流恒压充满电；

(2) 静置1h，测量开路电压；

(3) 以2.3C放电电流进行脉冲放电，持续18s，记录18s中电压的变化，通过电压变化值和放电电流计算电池在该SOC值下的内阻值；

(4) 静置1h，以0.5C放电电流进行放电，将SOC调整至下一个测试点；

(5) 重复步骤(2)～步骤(4)，分别调整电池的SOC至1，0.9，0.8，0.7，0.6，0.5，0.4，0.3，0.2，0.1。

实验可得开路电压E和内阻随SOC变化的数据。整个实验过程在20℃条件下进行，温度由PARTNER恒温箱控制。图2为实验实测所得电池内阻和开路电压随SOC的变化关系。

在上述的3个电池系统方案中，由于电池系统的容量配置完全与驱动电机的功率成比例，因此若按驱动电机峰值功率的比例分配前后轴电机的驱/制动功率，且各个电池系统初始SOC都相同，则在电动车运行过程中，无论是集中式电池系统，还是分布式电池系统，可保持其SOC基本一致。据此，根据各电池包电池组电路并联关系，不难看出各电池包内阻R和开路电压E具有如下关系：

(2)

1.3 电池系统损耗模型

电动汽车中电池系统与电机驱动系统工作原理如图3所示。图中Pe为电机及其逆变器消耗(电动状态)或回馈(再生制动)的瞬时电功率(以下统称为瞬时电机功率)。电池系统回路电流[7]为

(3)

电池内阻损耗功率P可由电流的平方与内阻之积表示：

(4)

分布式电池系统A内阻损耗功率为

(5)

分布式电池系统B内阻损耗功率为

(6)

集中式电池系统内阻损耗功率为

(7)

式中：Pef和Per分别为前后轴单个轮驱动电机的瞬时电功率。

可见，电池系统内阻损耗与电池的内阻、开路电压和电机瞬时功率分配有关。电池内阻与开路电压为SOC的函数，而电机瞬时功率分配影响着SOC的变化。由此可知，电机瞬时功率分配是影响电池内阻损耗的关键因素。

2 理论对比分析

设定不同分布形态的电池系统初始SOC一致，并令：

式中：C1和C2分别为分布式电池系统A和B的内阻损耗功率与集中式电池系统内阻损耗功率之差。由式(5)～式(7)，并结合式(2)，可得

(8)

可见分布式电池系统A与系统B的内阻损耗功率相等。

若令C1=0，可得Pef=2Per。这表明当前后轴电机功率分配(m=Pef/(Pef+Per))为2∶1时，分布式电池系统A与集中式电池系统内阻损耗功率相等。

令C1分别对Pef和Per求偏微分得

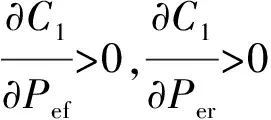
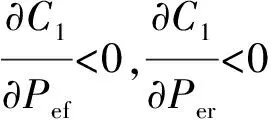
由此可知，在Pef=2Per处，C1取得最小值0，当Pef≠2Per，C1>0，因此C1≥0。

由于C1=C2，所以C2≥0同时成立。

由以上可知，当不同分布形态的电池系统SOC变化一致时，集中式电池系统内阻损耗不大于分布式。

3 工况仿真分析

对于分布式电动汽车，当车辆实际运行时，为了提高驱动系统的能量利用率，通常前后轴电机瞬时功率分配比是不固定的，而是以能量效率最优(能耗最优)为目标，在不同的驱动功率需求下，采取不同的前后轴电机瞬时功率分配。这也意味着分布式电池系统各电池包之间，及其与集中式电池系统电池包的SOC变化必然不一致。因此，在这种情况下，由式(2)所确定的各种电池包内阻的固定比例关系便不再成立，而是随各电池包的SOC状态改变。此时，采用理论方法分析得出的结论也不再成立。为此，本文中针对这种情况采用工况仿真的方法对分布式电池系统与集中式电池系统在实际工况运行时的能耗特性进行分析与对比。

对于分布式电动汽车，前后轴轮驱动电机的驱动/制动控制策略对整车能耗有重大影响。本文中将在分布式驱动采用电驱动系统能量效率最优的前后轴轮驱动电机瞬时电功率分配控制策略条件下，仿真计算并对比分析两种分布式电池系统A，B与集中式电池系统内阻上的电能损耗特性。同时，也对采用固定的前后轴电机瞬时功率分配策略下的上述3种电池系统的内阻电能损耗特性进行仿真，以便对比。

3.1 仿真参数

仿真对象为某A0级电动汽车动力系统，车辆参数如表3所示。

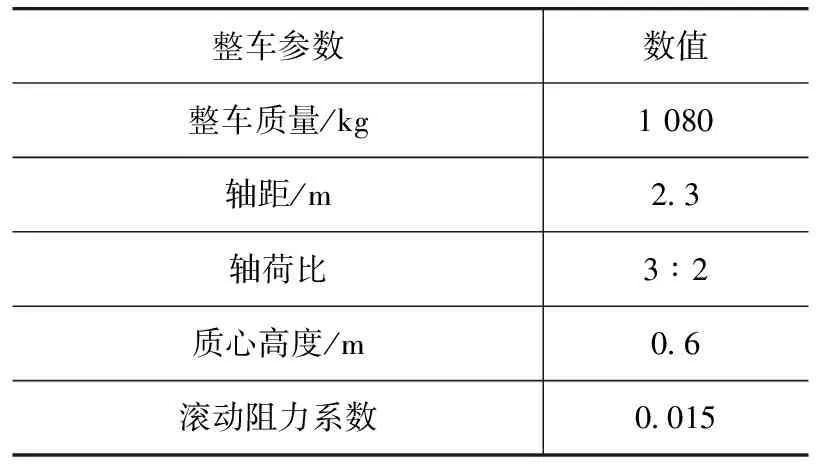
表3 车辆参数

前后轴轮驱动电机功率配置如表1所示，前后轴电机及其逆变器效率为实验测量值，如图4所示。

3.2 分布式驱/制动控制策略

如上所述，分布式驱动采用以整个驱动系统能量效率最优为目标的前后轴瞬时驱动转矩分配控制策略。

定义电机处于驱动状态时，其电功率Pe为正，电机处于制动状态时，其电机电功率Pe为负。采用整个工况下电机总驱动功率之和最小为目标函数，即

(9)

式中i为轮驱动电机序号。

驱动工况下，以Pe为优化目标，前后轴电机的输出转矩Tfe和Tre为优化变量，前后轴的驱动转矩之和为整车需求驱动转矩Tm，输出电流I不大于电池的最大输出电流和满足前后轴电机外特性等为约束条件，则驱动工况的优化模型为

(10)

式中：Tfmax和Trmax分别为前后轴电机最大转矩；Idiscmax为电池最大输出电流；ηmf和ηmr分别为前后轴电机瞬时效率；nf和nr分别为前后轴电机转速；if和ir为前后轴减速器速比。

制动工况下，以Pe为优化目标，前后轴电机的再生制动转矩Tfe和Tre及各轮液压制动力Tfm和Trm为优化变量，电机再生制动转矩与液压制动转矩之和为整车需求制动转矩Tm，以及满足前后轴电机外特性和ECE法规等约束条件，则制动工况的优化模型为

(11)

式中：Tfm和Trm为前后轮液压制动转矩；Wf为前轴载荷；q为制动强度；Ichmax为电池最大充电电流。

令k为前后轴电机转矩分配系数，即

(12)

通过离线的优化方法计算确定前后轴电机在驱/制动工况下最优转矩分配系数矩阵，见图5。

同时，也对以前后轴电机功率固定分配比为2∶1作为对比的瞬时转矩分配策略进行了仿真分析。

3.3 仿真结果分析

基于AMESim和Simulink建立仿真平台，其中，整车模型中用到AMESim集成的模块主要有驾驶员、整车、电池、逆变器、电机、减速器和制动系统等，驱/制动控制算法则在Simulink中建立。

选择新欧洲循环驾驶工况(NEDC)进行仿真测试，为了方便观测电池系统SOC的变化，选择10个测试循环。图6为两种控制策略下在单个测试循环下的车速，可以看出，两种控制策略均能使车辆满足工况的速度和加速度要求，能够使实际车速很好地跟随目标车速。

仿真结果如表4所示，可以看出：

(1) 在能量效率最优控制策略下，分布式电池系统A与系统B内阻损耗近似相等，对于驱动工况，相比于集中式电池系统，分布式电池系统内阻损耗增加56.87%，而在制动工况中，内阻损耗增加35.89%；

(2) 在2∶1的固定转矩分配比控制策略下，集中式电池系统与分布式电池系统A，B内阻损耗近似相等；

(3) 相比于能量效率最优控制策略，采用2∶1的固定转矩分配比控制策略，在驱动工况下，电机能量消耗增加6.9%，在制动工况下，电机回馈能量减少3.3%。

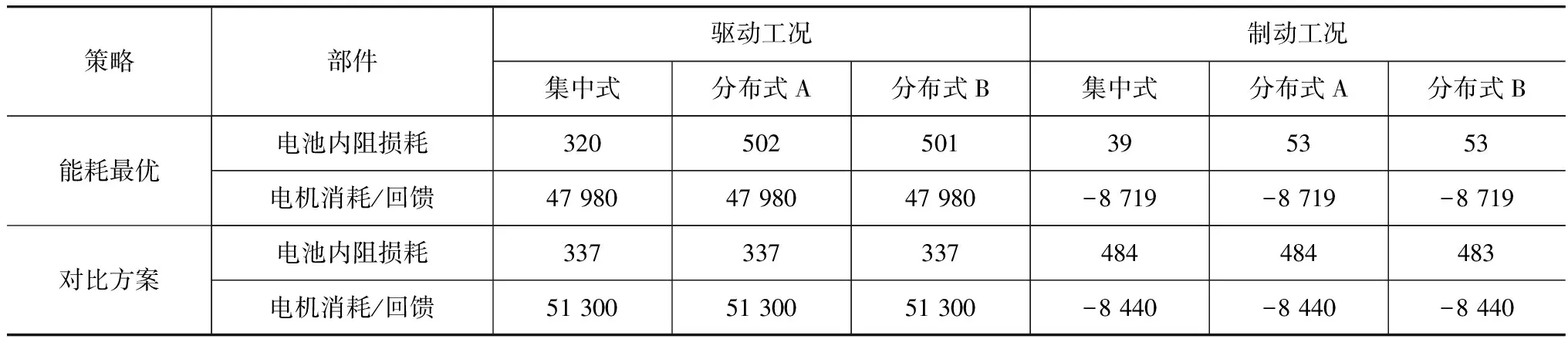
表4 仿真结果 kJ

由此可得到以下结论：在两种转矩分配控制策略下，集中式电池系统内阻损耗均不大于分布式电池系统。

前后轴电机在单个循环工况下功率分配如图7所示。

从图中可以看出，在2∶1的固定转矩分配比控制策略下，前后轴电机瞬时功率按照2∶1固定的比例分配，而在能量效率最优转矩分配控制策略下，前后瞬时功率分配根据实际工况进行调整。

由此可知，分布式电池系统只有在前、后轴电池包容量配置比与前后轴轮驱动电机功率配置比一致时，且车辆运行时前后轴电机瞬时功率按此配置比固定分配时才能实现电池内阻功率损耗特性最优。然而在实际运行时，按照固定值分配前后轴电机瞬时功率可能造成电机驱动系统能耗增加，导致整个动力系统能耗增加。相比于分布式电池系统，集中式电池系统无论在何种控制策略下均能保证内阻损耗最小。

此外，各电池系统SOC变化曲线如图8所示。从图中可以看出，在2∶1的固定转矩分配比控制策略下，集中式电池系统与分布式电池系统SOC变化一致，由初始值60%下降至29.54%。在能量效率最优控制策略下，分布式电池系统A与系统B的SOC变化一致，但对每一种系统其前后轴电池包的SOC变化不一致。前轴电池包SOC下降至34.84%，后轴电池包下降至25.73%，集中式电池系统下降至31.97%。可见，分布式电池系统各电池包会由于其充/放电功率不一致而引起SOC变化不均衡。对分布式驱动若采用分布式电池系统，这一特点必然会导致增加整车电池充电系统的设计难度。

4 结论

(1) 分布式驱动电动汽车，采用集中式电池系统，其内阻能耗特性要优于分布式电池系统。

(2) 从降低整车电池车载充电系统设计难度的角度，采用集中式电池系统也是合理的选择。

[1] 余卓平,冯源,熊璐.分布式驱动电动汽车动力学控制发展现状综述[J].机械工程学报,2013,49(8):105-114.

[2] 蔡卫兵.四轮独立驱动电动汽车节能控制策略研究[D].长春:吉林大学,2013.

[3] 李刚.线控四轮独立驱动轮毂电机电动汽车稳定性与节能控制研究[D].长春:吉林大学,2013.

[4] 杨鹏飞,熊璐,张康,等.分布式电驱动汽车稳定性控制策略设计与试验[J].机械工程学报,2013,49(24):128-134.

[5] 林成涛,仇斌,陈全世.电流输入电动汽车电池等效电路模型的比较[J].机械工程学报,2005,41(12):76-81.

[6] Johnson V. Battery Performance Models in ADVISOR[J]. Journal of Power Sources,2002,110(2):321-329.

[7] 胡明辉,秦大同.混合动力汽车镍氢电池组的充放电效率分析[J].重庆大学学报,2009,32(3):279-282.

A Study on the Effects of Distribution Pattern of Battery System on theEnergy Consumption Characteristics of Distributed Drive EV

Sun Zechang1,2, Zeng Yingjie1,2& Dai Haifeng1,2

1.ShoolofAutomotiveStudies,TongjiUniversity,Shanghai201804；2.CleanEnergyAutomotiveEngineeringCenter,TongjiUniversity,Shanghai201804

The energy consumption characteristics of battery system with different distribution patterns are analyzed for four-wheel distributed drive electric vehicles, a model for the energy consumption on the internal resistance of battery system is built based on Rint equivalent circuit model, and the energy consumption characteristics of both distributed and centralized battery systems are analyzed by theoretical calculation. Then a simulation platform for the energy consumption characteristics of electric vehicle is set up with AMESim/Simulink software, and aiming at the optimal torque distribution of driving motors in both front and rear axles with minimizing driving energy consumption as objective, a simulation on the energy consumption on the internal resistance of battery system is conducted with NEDC driving cycle. The results of both theoretical analysis and simulation indicate that the energy consumption characteristics with centralized battery system is superior to that with distributed system, which also has a problem of inconsistent SOC, leading to the complexity of on-board charging system design.

EVs; distributed battery system; centralized battery system; energy consumption characteristics

*国家重点基础研究发展计划(973计划)(2011CB711202)资助。

原稿收到日期为2014年3月27日，修改稿收到日期为2014年6月28日。