基于序列径向基函数的多目标优化方法及其应用

陈国栋，卜继玲

(株洲时代新材料科技股份有限公司，株洲 412007)



2015185

基于序列径向基函数的多目标优化方法及其应用

陈国栋，卜继玲

(株洲时代新材料科技股份有限公司，株洲 412007)

针对工程多目标优化求解耗时且全局高精度代理模型难以构造的问题，提出基于序列径向基函数的优化方法。该方法在每个迭代步，运用信赖域更新技术将整个设计空间分割成一系列信赖域，以降低优化问题的复杂程度。在每个信赖域上建立各个响应的代理模型，并采用微型多目标遗传算法进行优化。为避免序列近似优化引起的效率降低问题，运用继承拉丁超立方试验设计继承上一代样本点，以减少新样本；同时继承当前的非支配解，对代理模型局部加密，以减少迭代次数。在Benchmark测试问题中，与传统的代理模型方法相比，在实际模型相同调用次数情况下，该方法能更好地逼近全局前沿面。最后将该方法应用于某轿车车身结构轻量化问题中，验证了解决实际工程多目标优化问题的能力。

车身结构；多目标优化；序列径向基函数；耐撞性；轻量化

前言

在实际工程优化问题中，目标和约束函数通常不能显式表达，而采用耗时长的计算模型获得。优化是个迭代的过程，传统优化算法耗费大量的计算机资源，优化效率低下甚至失去实际工程意义。为解决效率问题，代理模型[1-3]常用于实际优化问题中。考虑到实际工程问题的复杂性，在整个设计空间构造的代理模型精度较低，导致基于此代理模型的优化精度较差[4]。于是一些代理模型管理方法发展起来，通过在优化过程中更新样本点或设计变量区间，重新构造代理模型。文献[5]中研究了智能布点更新代理模型的方法，并将其成功应用于车身薄壁构件的耐撞性问题。文献[6]中采用动态径向基函数，逐步更新重点采样空间并在其内部增加样本点来更新代理模型，该方法成功解决了NASA减速器优化设计问题。文献[7]中通过不断修改变量区间，将序列响应面法用于结构件和整车耐撞性的优化设计中，取得了较好的效果。

实际工程设计通常是个多目标优化问题。由于多目标问题的复杂性和解的不唯一性，缺乏高效的多目标的代理模型管理方法。文献[8]中根据代理模型获得Pareto解的分布情况，按照最小最大距离原则加密样本空间，该方法可较好地应用于无人机机翼结构优化问题中。随着设计变量和实际问题复杂性的增加，这种模型管理方法作用有限。文献[9]中通过响应面结合信赖域的方法处理多目标问题，在测试函数中取得了很好的结果，并成功应用于汽车覆盖件成型中，但该方法须在不同信赖域重新采样，计算量增加。

鉴于此，本文中提出一种高效的序列径向基函数方法(sequential radial basis function, SRBF)。该方法将整个设计空间上的复杂问题转化为一系列子空间上的简单问题，降低了代理模型精度对求解精度的影响。同时采用继承拉丁超立方(ILHD)试验设计和样本局部加密技术，避免序列近似多目标优化过程引起样本的增加。该方法在Benchmark测试问题中，相同实际模型调用次数下，与代理模型方法相比，体现了更好地逼近全局前沿面的能力。最后该方法成功应用于整车耐撞性和轻量化多目标优化中，获得了满意的结果。

1 序列径向基函数多目标优化方法

多目标优化问题数学模型的一般形式为

(1)

式中：f和g分别为优化目标和约束，m和p分别为优化目标和约束的数目，且m≥2；x为设计变量，xl和xu为其上、下边界。实际工程问题中，f和g通常表达为计算模型，如计算流体力学(CFD)模型和有限元(FEM)模型等。通常这些计算模型求解须耗费大量计算机资源，如单次汽车空气动力学分析需要几十小时，单次整车碰撞分析计算需要几十到上百小时。为提高优化效率，代理模型被用来近似表达上述优化问题。实际问题是个复杂的系统，设计变量和响应的关系复杂，当前代理模型技术很难获得精确近似。于是本文中将式(1)在整个设计空间上的复杂问题，转化为式(2)的一系列子空间(信赖域)上的简单问题。

(2)

在每个信赖域上近似求解，不论问题有多复杂，通过信赖域的缩放、平移，总能得到与实际模型一致的非支配解集，降低了代理模型精度对多目标求解精度的影响。但序列优化须在每个信赖域上重新采样来重构代理模型，降低了优化效率。于是采用继承拉丁超立方试验设计，并继承当前的非支配解对代理模型局部加密，避免序列过程引起样本的增加。整个优化流程如图1所示。

1.1 试验设计方法

本文中采用最优拉丁超立方(LHD)和继承拉丁超立方分别作为初次迭代和后续迭代的试验设计方法。LHD被称为一种“填充空间的设计”[10]，采用模拟退火法以最大化最小距离准则，使样本点在整个设计空间均匀分布。

当上一代的样本落在当代信赖域，ILHD可以继承这些样本并产生少量新样本。继承的样本和新样本依然保持拉丁超立方结构[11]，它们作为当代样本，大大减少了样本个数。以图2某二维设计空间为例，一次序列可以减少两个样本，这对样本获得耗时的汽车碰撞等工程问题具有重要意义[12]。

1.2 径向基函数代理模型

构造代理模型有几种常见的方法，如响应面(RSM)、Kriging(KRG)、径向基函数(RBF)等。文献[2]中研究发现，在汽车耐撞性方面，RBF比响应面能获得更好的近似。文献[13]中对4种代理模型进行比较，发现在考虑精度和鲁棒性情况下，RBF最可靠。RBF容易构造，是一种插值方法，其数学模型为

(3)

式中：ns为样本点个数；ri为待测点x与第i个样本点间的欧氏距离；φ为高斯基函数；wi为权系数。根据ns个样本点插值条件，计算得到wi，进而可以在整个设计域上进行近似。

1.3 微型多目标遗传算法

采用微型多目标遗传算法(μMOGA)[14]求解式(2)构造的多目标问题。μMOGA采用小规模进化种群，一般为5～8个，从而减少适应度计算次数。

采用重启动策略和个体拥挤距离比较机制保持进化种群中个体基因多样性。最优个体保存策略避免种群过早地局部收敛。重启动时加入了一种探测算子在可行域中进行探测性的局部搜索，分别在非支配解分布密集和分布稀疏区域各产生一个新个体，进一步加快收敛速度。通过大量测试函数比较，μMOGA能比NSGAⅡ更快地收敛到Pareto前沿，同时解集分布更均匀[14]。

1.4 信赖域更新技术

信赖域越小，代理模型越能更好地找到此区域上与实际模型一致的Pareto解。信赖域更新技术包括缩放和平移：根据信赖域不断缩放得到在该局部区域内与实际模型一致的Pareto解；通过信赖域不断平移得到在整个区域内与实际模型一致的Pareto解。信赖域更新通过更新信赖域半径和中心实现。

信赖度ρ衡量代理模型与实际模型的一致程度：

(4)

信赖域的缩放通过半径Δ的调整来实现，Δ由信赖度ρ来决定。

(5)

与全局优化不同，多目标优化的信赖域中心是个区域，不是一个点。它不仅影响下代信赖域的平移还影响下代信赖域的大小。本文中它由信赖度ρ、本代新获得的Pareto解个数和系数Rc决定。信赖域半径和中心确定后，信赖域区间由下式表达：

当ρ(k)≤Rc时，

(6)

当ρ(k)>Rc时，

(7)

以二维设计空间为例[12]，信赖域更新见图3。

1.5 样本局部加密技术

通过试验设计获得的样本在设计空间上均匀分布，而RBF是一种插值模型，在样本点处误差为零。在某些更有可能是Pateto解的区域，进行局部样本加密，可以提高Pateto解区域模型精度，更好地近似求解，减少迭代次数。

若当前获得的通过实际模型验证过的Pareto解落在下一代信赖域，将这些解添加到样本空间，在Pareto解处加密。这些加密点已经通过实际模型验证，不会增加计算时间。如果构造RBF的样本聚集，矩阵求解困难会造成代理模型不稳定，精度可能急剧减低。采用最小距离最大准则[15]挑选Pareto解作为加密点，保证加密后样本保持均匀。

(8)

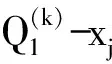
i≤n(Q(k)),j≤ns

(9)

2 序列径向基函数优化方法的验证

为了验证本文中的方法，采用经典的多目标测试函数进行测试。并与ISIGHT优化软件中基于代理模型的多目标优化方法进行比较。其中，首先采用LHD采样，再分别建立RSM，RBF和KRG代理模型，最后采用NSGA-Ⅱ[16]求解(种群数50，迭代100次)。在不同方法下，采用相同个数样本点情况下，比较Pareto解相对实际前沿面的分布情况。

测试函数1[9]：

(10)

测试函数2[9]：

(11)

由于基于代理模型方法找到的解集在目标空间的象点是通过代理模型计算的，与实际模型可能会有较大误差，而最终设计问题都要转化到实际模型。根据获得的近似前沿面分布情况，按照分布原则从中挑选出部分进行实际模型验证。采用收敛性能参数Υs和分布性能参数Δs对各个算法的求解性能进行量化的评价[16]。Υs越小表示求解精度越高，收敛性越好。Δs越小表示获得的Pareto解集在目标空间中的象点分布越均匀。

测试函数1，SRBF迭代2次收敛，优化过程中调用实际模型33次，其中包括找到的13个Pareto解。3种传统的代理模型方法中，均采取20个样本，再从近似优化中按照分布原则选择13个进行实际模型验证，并与样本点进行非支配排序，获得最终的近似前沿面。全局Pareto前沿面由2部分组成，不同方法找到的解如图4所示。SRBF，RBF和KRG的近似前沿面都分布在全局Pareto前沿面(解析解)上，如表1所示，收敛性能参数都小于0.1，但SRBF的分布性能相对更好。RSM的优化结果较差，是因为约束g1的代理模型精度较差，近似获得的Pareto解集大部分不满足约束。

测试函数2，SRBF迭代11次收敛，优化过程中调用实际函数188次，其中包括38个Pareto解。3种代理模型方法均采样150个，近似多目标优化后挑选38个进行验证。全局前沿面由4部分组成，不同方法找到的解如图5所示。SRBF的近似前沿面较均匀地分布在全局前沿面附近。而RSM，RBF和KRG的优化结果都不理想，由于它们近似多目标优化的解集在目标空间的象点与实际模型有较大误差，从而造成非支配解个数偏少。如表2所示，其他方法的收敛特性也不好，主要原因是函数f2非线性程度高，特别是包括绝对值的非连续和三角函数的振荡响应。

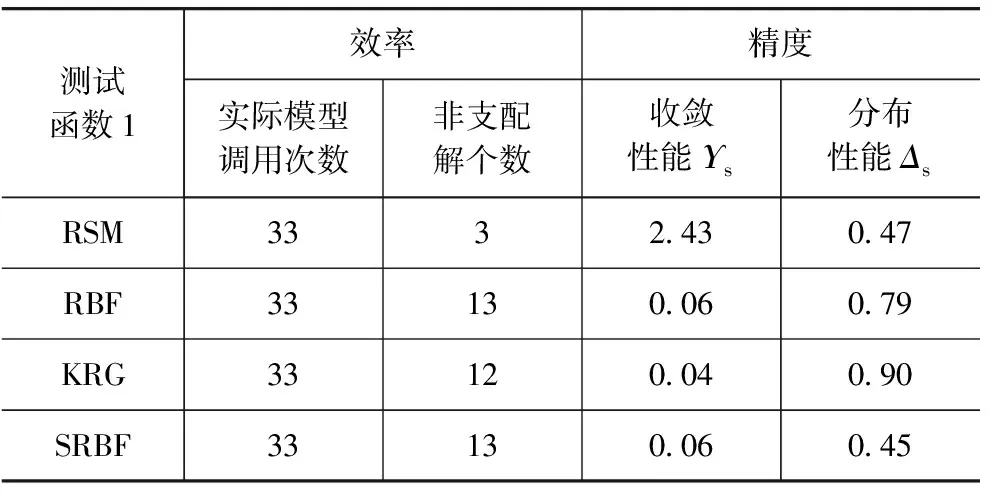
表1 测试函数1优化结果对比

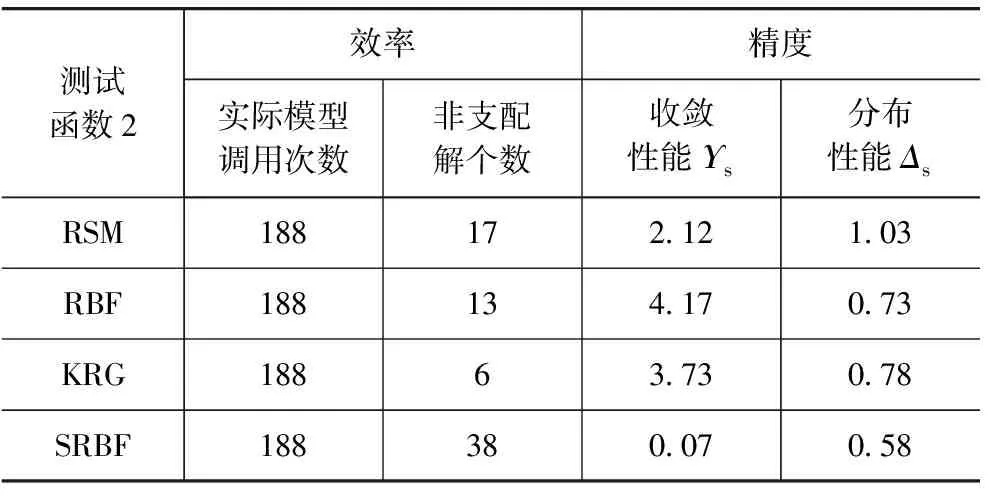
表2 测试函数2优化结果对比

通过测试函数发现，对于非线性程度一般情况，各种方法在相同计算机耗费(调用实际模型相同次数)情况下结果相当。随着非线性程度增加，如测试函数1，RSM方法不如RBF，KRG和SRBF。而当非线性程度较高时，如测试函数2，SRBF体现出明显的优势。主要是因为SRBF将复杂非线性设计空间分割成一系列信赖域，在每个信赖域上近似求解，降低了代理模型精度对求解精度的影响。

3 在轿车车身结构轻量化中的应用

以某型三厢轿车为例，综合考虑车顶准静态压溃、白车身模态和轻量化，通过结构改进，采用前面介绍的SRBF方法，进行车身结构的优化设计。

3.1 车顶准静态压溃分析

发生滚翻事故时，汽车车顶受冲击载荷而侵入乘客舱，造成人体损伤。提升车顶耐撞性，使其具备足够的强度，从而减小车顶的侵入，对确保乘员生存空间具有重要意义。

按照美国联邦机动车辆安全标准FMVSS 216，用762mm×1829mm的刚性墙以侧倾角25°和俯仰角5°对水平放置的某款轿车进行加载，如图6所示。考虑到显式动力学求解需要时间较长，采用提高加载速度(223.52mm/s)的方法进行准静态模拟。文献[17]中系统地研究了不同加载速度对车顶压溃仿真的影响，结合试验发现0.5mph(223.52mm/s)速度下，分析结果最稳定并且精度最高。测量车顶作用力峰值与压溃位移的关系，评价车顶耐撞性。峰值越大，耐撞性越好。图7为车顶作用力与压溃位移曲线，仿真与试验曲线变化趋势吻合[17]，作用力峰值误差为0.31%。

3.2 白车身模态

白车身自由模态分析主要用于获得振动的固有频率和振型，不仅反映了车身的整体刚度特性，而且是控制车身振动的关键指标。

在Hypermesh中建立有限元模型，自由边界。白车身由薄壁冲压件焊接而成，薄壁构件采用壳单元模拟，焊点在实际焊点位置通过rigid单元模拟。壳单元以四边形单元为主，避免过多的三角形单元引起局部刚性过大。其整体1阶扭转模态为26.4Hz，振型如图8所示。汽车的激励主要来自路面、车轮、发动机等，车身的1阶模态要错开分量较大的激励频率，特别是发动机怠速激励频率，结合标杆车指标，该白车身的1阶扭转模态应高于25Hz。

3.3 多目标优化问题的建立

根据FMVSS 216标准，以车顶作用力峰值最大为目标。若只考虑提升车顶耐撞性，通常会增强车身结构，导致车体质量增加，故选择整车质量为另一个目标。由于车身结构参数多，筛选出对目标影响大的部分，以减少优化过程中耗费的计算机资源。采用Sobol法进行全局灵敏度分析[18]以筛选设计变量。最终选择了9个部件厚度作为设计变量，如图9所示。其中A柱、B柱等4个部件左右对称，对称部件可以作为一个设计变量考虑，于是最终设计变量为5个。由图8可见，白车身1阶扭转模态振型发生在A柱与横梁交接处，A柱和横梁厚度的改变会影响到白车身模态，所以选取1阶扭转模态作为约束，则可以建立以下多目标优化模型：

(12)

式中：f1为车顶作用力峰值；f2为整车质量；g为白车身整体1阶扭转自由模态；ti为敏感度大的结构部件厚度。

3.4 优化结果与分析

在每个信赖域，试验设计样本个数ns=15，挑选近似Pareto解个数na=10。对信赖域进行了局部样本加密技术，迭代4次就收敛。采用了ILHD试验设计，减少样本点17个。共调用有限元模型83次，其中Pareto解30个，如图10所示[12]。

根据法规和设计要求，从获得的Pareto解中挑选最终设计方案。FMVSS 216标准规定，车顶所能承受的作用力必须大于整车整备质量的1.5倍。由图10可见，30个方案都在FMVSS 216标准之上，都满足车顶耐撞性要求。若选择方案1，既通过FMVSS 216标准，又可以达到质量减轻4.6kg的效果。若同时考虑耐撞性和轻量化，可选择方案2，车顶最大作用力还增加0.24kN，并且质量减轻0.8kg。由于当前的标准偏低，美国公路安全保险研究所(IIHS)制定了新的规范，车顶所能承受的作用力提高到整车整备质量的2.5倍才能获得“合格”。根据新的规范，选择方案3，但质量增加5kg。

4 结论

(1) 本文中提出基于序列径向基函数的多目标优化方法，克服了代理模型在整个设计区间精度难以保证的问题，通过序列近似降低了实际工程问题的复杂程度。通过继承拉丁超立方试验设计和非支配解遗传局部加密技术，避免了序列过程引起的效率降低。

(2) 在两个Benchmark数学测试问题中，与传统基于代理模型的方法进行比较，在同等计算机耗费情况下，本文方法获得的多目标解集更均匀更靠近解析解，验证了该方法的求解精度。同时表明，随着优化问题非线性程度的增加，更能体现出该方法的优势。

(3) 该方法成功应用于汽车车顶压溃的耐撞性和轻量化多目标优化问题中。合理匹配A柱，B柱和横梁厚度，在满足白车身模态约束下获得大量Pareto解，根据法规需要或凭借经验，灵活选择最终的设计方案。验证了解决实际工程多目标优化问题的能力，为其它复杂工程优化问题提供借鉴。

[1] 王平,郑松林,吴光强.基于协同优化和多目标遗传算法的车身结构多学科优化设计[J].机械工程学报,2011,47(2):102-108.

[2] 张宏波,顾镭,徐有忠.基于博弈论的汽车耐撞性多目标优化设计[J].汽车工程,2008,30(7):553-556.

[3] Fang H, Rais-Rohani M, et al. A Comparative Study of Metamodeling Methods for Multi-objective Crashworthiness Optimization[J]. Computers & Structures,2005,83:2121-2136.

[4] 孙光永,李光耀,钟志华,等.基于序列响应面法的汽车结构耐撞性多目标粒子群优化设计[J].机械工程学报,2009,45(2):224-230.

[5] Wang H, Li G Y, et al. A Comparative Study of Boundary-based Intelligent Sampling Approaches for Nonlinear Optimization[J]. Applied Soft Computing,2011,11(2):2227-2238.

[6] 彭磊,刘莉,龙腾.基于动态径向基函数代理模型的优化策略研究[J].机械工程学报,2011,47(7):164-170.

[7] Kurtaran H, Eskandarian A, Marzougui D, et al. Crashworthiness Design Optimization Using Successive Response Surface Approximations[J]. Computational Mechanics,2002,29(4):409-421.

[8] An W G, Li W J, Gou Z Q. Multi-objective Optimization Design of Wing Structure with the Model Management Framework[J]. Chinese Journal of Aeronautics,2006,19(1):31-35.

[9] Liu G P, Han X, Jiang C. A Novel Multi-objective Optimization Method Based on an Approximation Model Management Technique[J]. Computer Methods in Applied Mechanics and Engineering,2008,197:2719-2731.

[10] Morris M D, Mitchell T J. Exploratory Designs for Computational Experiments[J]. Journal of Statistical Planning and Inference,1995,43(3):381-402.

[11] Wang G G. Adaptive Response Surface Method Using Inherited Latin Hypercube Design Points[J]. J. Mech. Des.,2003,125:210-220.

[12] 陈国栋.基于代理模型的多目标优化方法及其在车身设计中的应用[D].长沙:湖南大学,2012.

[13] Jin R, Chen W, Simpon T W. Comparative Studies of Metamodelling Techniques Under Multiple Modeling Criteria[J]. Structural and Multidisciplinary Optimization,2001,23:1-13.

[14] Liu G P, Han X. A Micro Multi-objective Genetic Algorithm for Multi-objective Optimizations[C]. The 4th China-Japan-Korea Joint Symposium on Optimization of Structural and Mechanical Systems,2006:419-424.

[15] Chen G D, Han X, Liu G P, et al. An Efficient Multi-objective Optimization Method for Black-box Functions Using Sequential Approximate Technique[J]. Applied Soft Computing,2012,12(1):14-27.

[16] Deb K. A Fast and Elitist Multi-objective Genetic Algorithm: NSGA-II[J]. IEEE Transactions on Evolutionary Computation,2002,6(2):182-197.

[17] Bathea K J, Walczak J, et al. Advances in Crush Analysis[J]. Computer and Structures,1999,72:31-47.

[18] 潘锋,朱平.基于支持向量回归技术的轿车车顶压溃耐撞性研究[C].2009中国汽车安全技术国际研讨会,2009:51-56.

An Multi-objective Optimization Scheme and Its ApplicationBased on Sequential Radial Basis Function

Chen Guodong & Bu Jiling

ZhuzhouTimesNewMaterialTechnologyCo.,Ltd.,Zhuzhou412007

In view of the problem of time-consuming solving and the difficulty in constructing global high-accuracy surrogate models in multi-objective engineering optimization, an optimization scheme based on sequential radial basis function is proposed. In each iteration with the scheme, the entire design space is divided into a series of trust regions by applying trust region update technique to reduce the complexity of optimization problem. Then the surrogate model for each response is built in each trust region and an optimization is conducted with micro multi-objective genetic algorithm. To avoid low efficiency caused by sequential process, the sample points of previous generation is inherited by using inherited Latin hypercube design of experiment for reducing new samples, while with the current non-dominate solution inherited, the mesh of some localities in the surrogate model is densified to reduce the number of iteration. In benchmark testing, compared with traditional surrogate model method, the scheme proposed can better approximate global frontier with the same times the model is called. Finally, the proposed scheme is successfully applied to the body structure lightweight optimization of a car, verifying its capability in solving the practical engineering problem of multi-objective optimization.

car body structure; multi-objective optimization; sequential radial basis function; crashworthiness; lightweighting

原稿收到日期为2013年12月27日，修改稿收到日期为2014年5月7日。