电控汽油喷射器电磁特性仿真与磁路参数优化*

程 强，张振东，郭 辉，朱 希

(1.上海理工大学汽车工程研究所，上海 200093； 2.上海工程技术大学汽车工程学院，上海 201620)



2015114

电控汽油喷射器电磁特性仿真与磁路参数优化*

程 强1，张振东1，郭 辉2，朱 希1

(1.上海理工大学汽车工程研究所，上海 200093； 2.上海工程技术大学汽车工程学院，上海 201620)

依据电磁学和机械动力学理论，建立了电控汽油喷油器工作过程的计算模型，以分析其动态响应特性与磁路结构参数之间的耦合关系。以缩短电控汽油喷射器开启和关闭延迟时间为优化目标，利用多目标模拟退火算法对磁路结构参数进行了优化。采用Ansoft Maxwell电磁场仿真软件，对优化前后的磁力线、磁感应强度、电磁力和动态响应特性进行了仿真分析，并通过试验对优化结果进行了验证。结果表明，优化后的电控汽油喷射器的动态响应特性得到了明显的提高。

汽油喷射器；磁路结构；动态响应；多目标模拟退火算法

前言

汽车工业的飞速发展和排放法规的日益严格，对汽车发动机的强化程度提出了更高的要求，高速化和高效化已成为汽车发动机的发展必然趋势。电控汽油喷射器作为发动机电控汽油喷射系统中的核心部件，直接决定发动机燃油喷射量和雾化质量，从而影响发动机的动力性、经济性和排放性能[1-3]，因此，开发结构紧凑、性能稳定和响应迅速的电控汽油喷射器对提高发动机性能有着重要的意义。在磁路零件材料确定的条件下，磁路结构参数配置决定了电控汽油喷射器的动态响应特性。国内外学者针对汽油喷射器的磁路结构开展了一些研究工作：文献[4]中对磁路局部结构进行了改进，并利用电磁场仿真软件对改进结构进行了分析，验证了磁路结构对喷油器性能的重要作用；文献[5]中在不影响喷油器整体性能的条件下，针对不同的磁路结构参数进行了优化，完成了电控喷油器的小型化设计。上述研究，以多方案仿真对比为基础，并未在数学模型的基础上实现不同磁路参数的最佳匹配。近年来，随着研究的不断深入，各种优化算法不断应用于工程实际中[6-7]，而多目标模拟退火算法(MOSA)因其具有较强的鲁棒性、全局收敛性和广泛的适应性等显著优点，在工程优化问题中得到了较多的应用。文献[8]中采用该算法对柴油机高压共轨喷油器结构参数进行了优化设计，取得了较满意的效果；文献[9]和文献[10]中利用该算法作为寻优策略，对高压共轨喷油器进行了优化设计，从一定程度上提高了喷油器的动态响应特性。本文中在该研究的基础上，采用MOSA算法对电控汽油喷射器进行磁路结构优化，并结合电磁有限元仿真软件，建立多目标函数之间的内部联系，实现了优化算法、仿真分析和结构优化的无缝连接，为工程应用提供了有效的理论支撑。

1 汽油喷射器电磁理论与计算模型

1.1 磁路结构

电控汽油喷射器结构如图1所示，主要由铁芯、衔铁组件(包括衔铁、导流管和钢球)、导磁体、电磁线圈、弹簧、阀座和喷孔片等组成。其工作原理为：当线圈通电时，产生电磁场，电磁场在磁路结构中产生电磁吸力，当电磁吸力大于弹簧预紧力时，衔铁组件离开阀座向铁芯方向运动，此时球阀打开，燃油通过阀座与钢球之间的缝隙流出，经喷孔片上的微孔形成喷雾；当线圈断电后，电磁力逐渐消失，衔铁组件在弹簧作用下落座，完成喷射过程。

为便于建立磁路结构参数与电磁特性之间的数学模型，对磁路结构进行了简化，如图2所示，主要由铁芯、衔铁、导磁片、导向管和线圈等组成。在磁路结构中，由于软磁材料本身的磁导率远高于空气的磁导率，因此可忽略磁性元件本身的磁阻，汽油喷射器的磁阻主要由工作气隙磁阻和滑动气隙磁阻两部分组成。

1.2 磁路子模型

利用安培环路定律和虚功原理计算磁路结构中的电磁感应强度和电磁力：

∮Hdl=Ni

(1)

(2)

式中：H为磁场强度；l为磁路总长度；N为电磁线圈匝数；i为线圈单匝电流；Fmag为电磁力；Wco-energy为电磁力所做的功；gmax为工作气隙；x为衔铁位移；C1、C2为与磁阻有关的常数。

1.3 电路子模型

电控汽油喷射器的等效电路如图3所示。

由于驱动电路的附加电阻和电感比喷油器线圈的电阻和电感小得多，故可忽略不计，则由基尔霍夫电压平衡方程可得

(3)

式中：U0为驱动电压；i(t)为线圈电流变化函数；R为线圈电阻；L为线圈电感。

求解式(3)微分方程，可得

(4)

1.4 衔铁受力模型

电控汽油喷射器工作过程中受力情况较为复杂，如图4所示。

当电控汽油喷射器工作时，衔铁的受力Fn为

Fn=Fmag-(±Fflu+Fspring+G)

(5)

式中：Fmag为电磁力；Fflu为液压力，与电磁力方向相同为正；Fspring为弹簧预压力；G为衔铁组件的重力。

1.5 动态响应特性模型

电控汽油喷射器开启和关闭过程线圈电流与衔铁位移之间的对应关系曲线如图5所示。由图可知，开启和关闭过程可各分为两个阶段。开启过程见图5(a)：从线圈通电开始到衔铁钢球组件刚要运动时的开启触动过程(OB段)，此时线圈电流几乎呈线性增加，但是衔铁位移为0；衔铁组件从开始运动到最大行程时的开启运动过程(BC段)，此时在感应电流的作用下，电流稍有下降，衔铁加速运动。关闭过程见图5(b)：线圈断电到衔铁钢球组件刚要运动时的关闭触动过程(DE段)，此时电流下降，但是在磁滞作用下，仍有电磁力作用于衔铁，使衔铁与铁芯保持吸合状态；衔铁钢球组件的关闭运动阶段(EF段)，此时衔铁在弹簧力的作用下回位，关闭球阀。

联合式(1)～式(5)和不同阶段的初始条件，求解得出：

(6)

(7)

(8)

(9)

因此，喷油器开启时间为

topen=t1+t2

(10)

喷油器关闭时间为

tclose=t3+t4

(11)

2 多目标模拟退火算法(MOSA)

模拟退火算法采用了Metropolis-Hastings接受准则，具有可避免早熟和局部优化的特点，在工程中得到了广泛的应用[8]。该算法可求解非线性问题，对不可微甚至不连续的函数，能以较大概率求得全局最优解，特别适合对电控汽油喷射器进行多目标、多参数结构优化。

2.1 优化参数及其约束条件的设定

本文中以某款电控汽油喷射器初始结构为基础，对其磁路参数进行优化。通过理论分析并结合工程实际，确定了8个须优化的关键磁路参数及其变化范围，如表1所示。

2.2 目标函数与数学模型

电控汽油喷射器的动态响应特性主要由开启和关闭延迟时间两个参数表征，本文以此作为目标函数：

f1(X)=topen

(12)

f2(X)=tclose

(13)

根据多目标优化算法建立优化模型为

表1 汽油喷射器磁路结构参数约束范围

(14)

式中：ω1、ω2为加权系数；Xmin和Xmax数值见表1。

2.3 MOSA优化算法的实现

(1) 控制参数的设置

根据MOSA算法加温、等温、冷却过程的要求和Metropolis接受准则，选取温度控制参数见表2。

表2 MOSA算法控制参数

(2) 初始解求解

对于汽油喷射器所对应的结构参数集合{X1，X2，X3，X4，X5，X6，X7，X8}，随机选取其约束条件内的一组参数{x1，x2，x3，x4，x5，x6，x7，x8}，作为初始解S1，令T=T0，其中，Tk+1=Tkexp(-qk)，并根据链长L，确定每个温度时的迭代次数。

(3) 解变换生成新解

采用二邻域变换法对当前解S1进行变换，产生新的路径，即新的可行解S2。

(4) Metropolis接受准则

假设路径长度函数为f(S)，则当前解的路径为f(S1)，新解的路径为f(S2)，路径差为df=f(S1)-f(S2)，根据Metropolis接受准则：

(15)

当df<0时，以概率1接受新的路径；当df≥0时，则以概率exp(-df/T)接受新的路径。

2.4 计算结果分析

采用MOSA算法对电控汽油喷射器磁路结构进行优化计算，优化前后的关键磁路结构参数如表3所示。

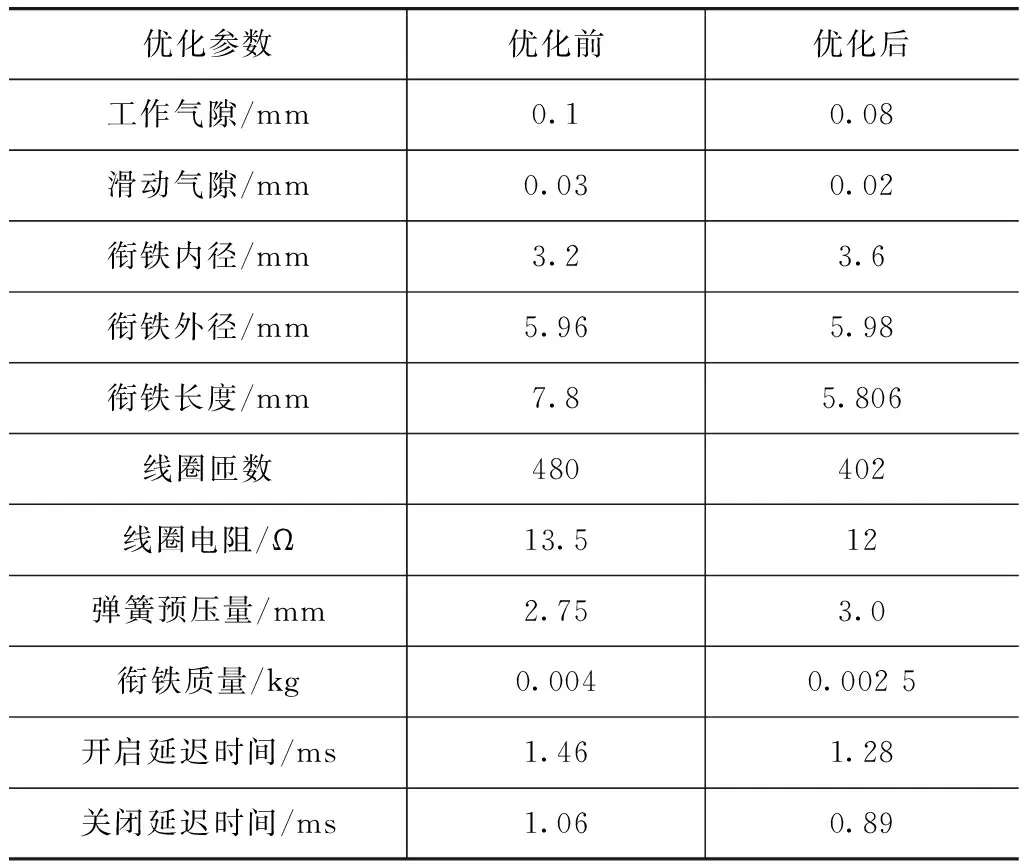
表3 优化前后结构参数对比

3 磁路优化效果验证

3.1 仿真结果分析

采用Ansoft Maxwell电磁场有限元仿真软件，对优化前后的磁力线分布、磁感应强度和电磁力及动态响应性能进行了仿真分析。由于本文中电控汽油喷射器为对称结构，故只须分析其1/4模型。优化前后磁力线和磁感应强度分布与变化规律如图6和图7所示。由图6可见：优化前部分磁力线直接从导向管到导磁片溢出，造成漏磁；优化后导向管与导磁片之间无漏磁现象发生。由图7可见：优化前衔铁、铁芯磁感应强度达到最大，磁通密度达到饱和；优化后，磁通密度分布更加合理，衔铁体积变小，但是磁感应强度并不受影响。

图8和图9分别为仿真所得的电磁力变化曲线和电流变化曲线。由图8可见，虽然优化后的最大电磁力比优化前下降8%左右，但在开启阶段，电磁力上升速度和落座阶段电磁力的下降速度明显快于优化前，有利于提高衔铁钢球组件的动态响应速度。图9的电流变化曲线验证了该结论，优化前，开启和关闭延迟时间分别为1.53和1.30ms，优化后，开启和关闭延迟时间分别为1.08和0.92ms，分别缩短了29.41%和29.23%。

3.2 试验结果分析

为了深入研究优化前后的电控喷油器性能，对优化后的电控汽油喷射器进行了样品试制，并利用动态响应特性测试仪[3]测定了不同驱动电压、弹簧预压力和燃油压力下的开启和关闭延迟时间，结果如图10～图12所示。

由图10可见，开启延迟时间随着驱动电压的增加而缩短，关闭延迟时间随着驱动电压的增加而延长。这主要是由于当驱动电压增加时，线圈储能也增加，衔铁组件所受电磁力增大，开启速度加快，而由于储能越多，释放能量的时间越长，因此，关闭延迟时间延长。由于优化后，衔铁的质量变轻、气隙位移缩短和线圈匝数减少，这些参数的优化使动态响应明显变快。

由图11可见，随着弹簧预压力的增加，开启延迟时间延长，关闭延迟时间缩短。根据式(5)可以看出：弹簧预压力越大，电磁力所需要克服的力越大，衔铁的加速度越小，所以开启延迟时间延长；关闭时，弹簧预压力越大，衔铁的加速度越大，关闭延迟时间越短。优化后动态响应时间明显优于优化前。

由图12可见，随着燃油压力的增加，开启延迟时间延长，关闭延迟时间缩短。根据式(5)可以看出：燃油压力越大，当作用面积不变时，电磁力所需要克服的力越大，衔铁的加速度越小，所以开启延迟时间延长；关闭时，燃油压力与衔铁组件运动方向相同，燃油压力越大，衔铁的加速度越大，关闭延迟时间越短。优化后动态响应时间明显优于优化前。

4 结论

(1) 在电磁理论和机械动力学的基础上，结合通电后衔铁钢球组件的运动特点，建立了电控汽油喷射器动态响应特性的计算模型，并推导出动态响应特性时间参数与结构参数之间的数学关系。

(2) 采用MOSA算法，以开启和关闭延迟时间为目标函数，以电控汽油喷射器的磁路参数为研究对象，对其结构参数进行了匹配优化。

(3) 从电磁场仿真和试验两个方面，对MOSA优化算法的有效性进行了验证，并采用试验手段分析了优化前后的样品在不同驱动电压、弹簧预压力和燃油压力条件下开启和关闭延迟时间，进一步证明了MOSA算法的工程应用价值。

[1] 邸立明,韩宗奇,夏怀成,等.电控喷油器流量特性的仿真研究[J].汽车工程,2009,31(5):451-456.

[2] 罗贤才,张振东,程强,等.进气歧管喷射式电控喷油器磁路结构改进研究[J].上海理工大学学报,2013,35(1):55-59.

[3] 郭辉,张振东,程强,等.一种电控喷油器动态时间参数测试方法[J].中国机械工程,2012,23(5):626-628.

[4] Hideyuki Watanabe, Shinya Ichise, Takahiro Nagaoka, et al. Development of Compact and High Performance Fuel Injector Using Electromagnetic Field Simulation[C]. SAE Paper 2005-32-0019.

[5] Dean Cvetkovic, Irena Cosic, Aleksandar Subic. Improved Performance of the Electromagnetic Fuel Injector Solenoid Actuator Using a Modeling Approach[J]. International Journal of Applied Electromagnetics and Mechanis,2008,27:251-273.

[6] 郭辉,张振东,孙跃东.电控参数优化及性能测试研究[J].中国机械工程,2010,21(18):2264-2267.

[7] 李铁栓,张幽彤,王定标.基于多目标模拟退火算法的高速电磁阀优化设计[J].车用发动机,2010(8):6-10.

[8] 熊庆辉,张幽彤.基于MOSA算法的高压共轨喷油器多目标仿真优化设计木[J].农业机械学报,2011,42(1):27-30.

[9] 熊庆辉,张幽彤,王定标.基于NSGA-Ⅱ算法的高压共轨喷油器优化设计[J].北京理工大学学报,2010,30(10):1160-1164.

[10] 袁文华,鄂加强,龚金科,等.自适应粒子群优化的高压共轨燃油喷嘴多学科优化设计[J].内燃机工程,2009,30(5):63-67.

Electromagnetic Characteristics Simulation and Magnetic Parameter Optimizationfor Electronically-controlled Gasoline Injector

Cheng Qiang1, Zhang Zhendong1, Guo Hui2& Zhu Xi1

1.InstituteofAutomotiveEngineering,UniversityofShanghaiforScienceandTechnology,Shanghai200093;2.CollegeofAutomotiveEngineering,ShanghaiUniversityofEngineeringScience,Shanghai201620

Based on electromagnetic theory and mechanical dynamics, a calculation model for the working process of electronically-controlled gasoline injector is established to analyze the coupled relationship between its dynamic response characteristics and the structural parameters of magnetic circuit. With minimizing the opening and closing time delays as objectives, the structural parameters of magnetic circuit is optimized by using multi-objective simulated annealing algorithm, and a simulation on the magnetic field line, magnetic induction intensity, electromagnetic force and dynamic response characteristics before and after optimization is conducted and verified by tests. The results show that the dynamic response characteristics of electronic fuel injector are obviously improved after optimization.

gasoline injector; magnetic circuit structure; dynamic response; MOSA algorithm

*国家自然科学基金(51275309)、上海市教委科研创新项目(13YZ110)、上海市研究生创新基金(JWCXSL1201)和上海工程技术大学校基金(2011xy28)资助。

原稿收到日期为2013年1月28日，修改稿收到日期为2013年11月11日。