基于改进小波变换和Zernike 矩的亚像素边缘检测算法
文 涛, 左东广, 李站良, 卫宾华
(第二炮兵工程大学,西安 710025)
0 引言
边缘检测作为计算机视觉和数字图像处理中的关键技术,其目的是要找出周围像素灰度有屋顶变化或阶跃变化的像素点的集合[1],从而为人们分析图像或描述目标提供有价值的信息。经典的边缘检测算法可以分为基于查找的边缘检测算法、基于零穿越的边缘检测算法和Canny 边缘检测算法3 类[2]。其中:基于查找的算法是基于一阶导数的边缘检测算法,该算法通过寻找图像一阶导数中的最大和最小值来检测边界,常用的微分算子有Roberts 算子、Sobel 算子、Prewitt算子等;基于零穿越的算法是基于二阶导数的边缘检测算法,该算法通过寻找图像二阶导数零穿越来检测边界,但是这种算法得到的边缘容易受噪声的影响。为此,美国学者MARR 将高斯低通滤波和拉普拉斯边缘检测结合在一起,提出了高斯—拉普拉斯算子(LOG)。
随着数字图像处理技术的广泛应用,人们对边缘检测算法的检测效果要求也在不断提高:一方面,人们希望检测算法能够对强噪声条件下弱目标做出检测[3];另一方面,人们希望边缘检测的定位精度从像素级提高到亚像素级。虽然传统的边缘检测算法原理简单且实时性好,但其无法满足高精确定位和强抗干扰性能的双重要求。
文献[4]中提出了一种基于小波系数的多尺度边缘增强算法,实现了SAR 图像的自动边缘增强和检测;文献[5]利用多尺度小波变换的边缘检测方法实现了对带有噪声的印刷电路板图像边缘的精确提取;文献[6]提出了改进的形态梯度算子和Zernike 矩的边缘检测算法,该方法能够很好地满足电荷耦合器件测量系统所需要的亚像素边缘检测。
因此,本文将小波变换和Zernike 矩结合起来,提出了一种多尺度模极大值亚像素边缘检测算法,该方法首先结合小波变换和小波模极大值原理,将边缘点由粗到细地搜索出来,实现边缘的准确、有效定位,然后再用改进后的Zernike 矩算子对图像进行进一步的亚像素边缘提取。实验结果证明,该方法与经典的边缘检测算法相比,抗噪能力强且边缘定位精度高,能够满足高精度图像测量应用。
1 小波模极大值边缘检测原理
通俗地讲,小波模极大值就是将小波函数与信号进行卷积运算,然后对计算结果取模,最后找到最大值。在图像处理中,小波变换的模极大值对应着图像的突变点,如噪声和边缘信息,因此,可以通过计算图像小波变换的模极大值来提取图像的边缘信息。
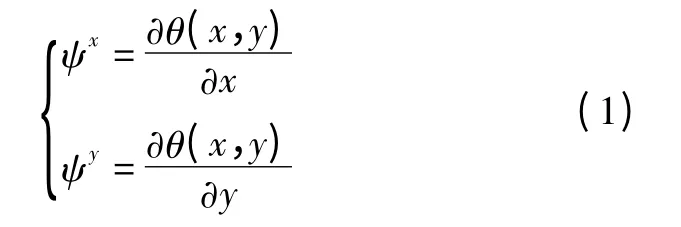
式中,ψx和ψy均满足积分为零的条件,可以将其看成两个二维小波函数。一般情况下,θ(x,y)取为二维高斯函数,其表达式和一阶偏导数表达式为
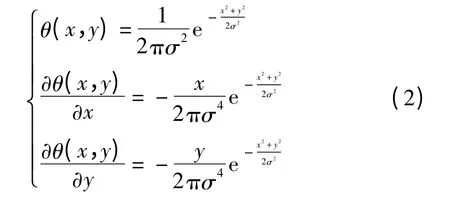
式中,σ 为正态分布的标准偏差。
对于f(x,y)∈L2(R)的任意图像来说,在尺度为s时的小波变换的两个分量分别为
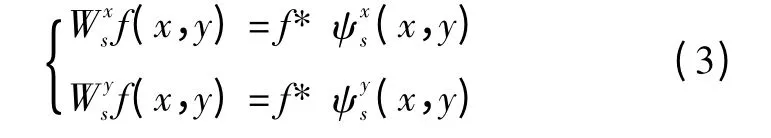
则小波变换在尺度s 下,梯度的模和幅角分别为
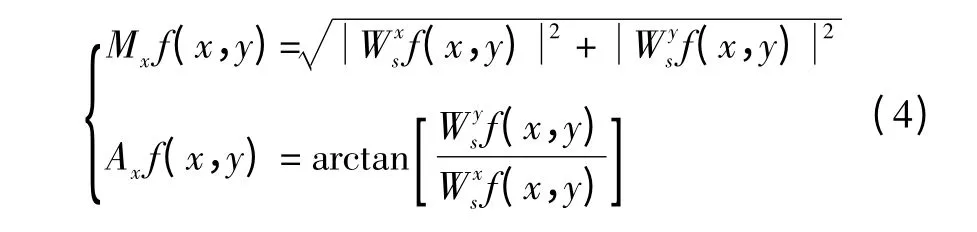
式中:f(x,y)为二维信号;L2(R)为函数空间。
梯度的模值Mxf(x,y)反映了图像在点(x,y)处的灰度变化程度,梯度的幅角Axf(x,y)是梯度向量与水平方向的夹角。因此,图像的边缘特征点为沿着梯度方向上模为局部极大值的点。
2 亚像素边缘检测算法
2.1 Zernike 矩原理
Zernike 矩的复数域n 阶多项式定义为
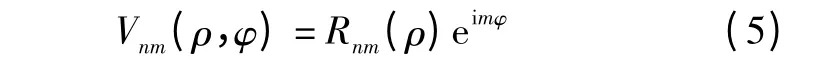
式中:m 和n 为整数,且n- |m|为非负的偶数;ρ 为原点到(x,y)的矢量长度;i 为虚数单位;径向多项式Rnm为
Zernike 多项式在单位圆内是正交的,即
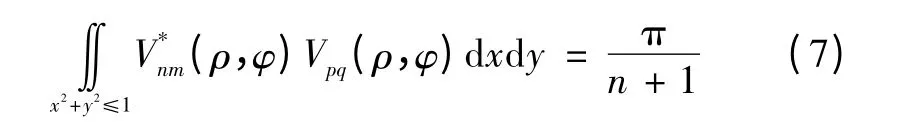
当且仅当n=p,m=q 时,式(7)成立,其中V*nm(ρ,φ)为Vpq(ρ,φ)的共轭。
连续图像f(x,y)的二维Zernike 矩定义为
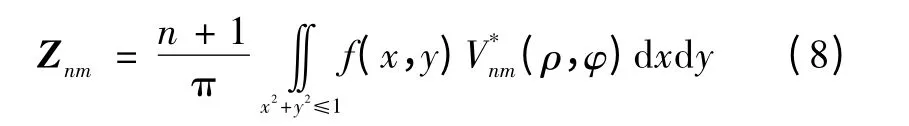
离散的数字图像f(x,y)的Zernike 矩可以表示为
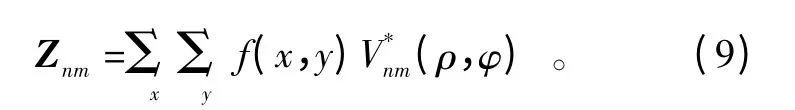
若图像旋转φ 角,则旋转之前的Zernike 矩Znm和旋转之后的Zernike 矩Znm' 之间有如下关系

从式(10)可看出,图像旋转前后只是相角发生了变化,而Zernike 矩的模不变,这个性质被称为旋转不变性。
2.2 基于Zernike 矩的边缘检测算法原理
基于Zernike 矩的边缘检测算法原理是通过建立Zernike 矩与理想的亚像素模型的4 个边缘参数的关系,分别求解矩而得到图像模型的4 个边缘参数,再将参数与预设的阈值进行比较判断,进而精确定位边缘点。平面亚像素阶跃边缘模型如图1 所示,其中,h 为背景灰度,k 为阶跃高度,l 为中心到边缘的距离,φ 为l与x 轴之间的夹角。
根据Zernike 矩原理可知,m 和n 为整数,且n -|m|为非负的偶数,因此可以得到5 个不同阶次的矩Z00,Z11,Z20,Z31,Z40。
根据式(6)可得部分径向多项式Rnm值如表1 所示。
表1 中,r 为原点到点(x,y)的长度。根据式(5)和表1 可以计算出Zernike 矩的复数域多项式如表2所示。
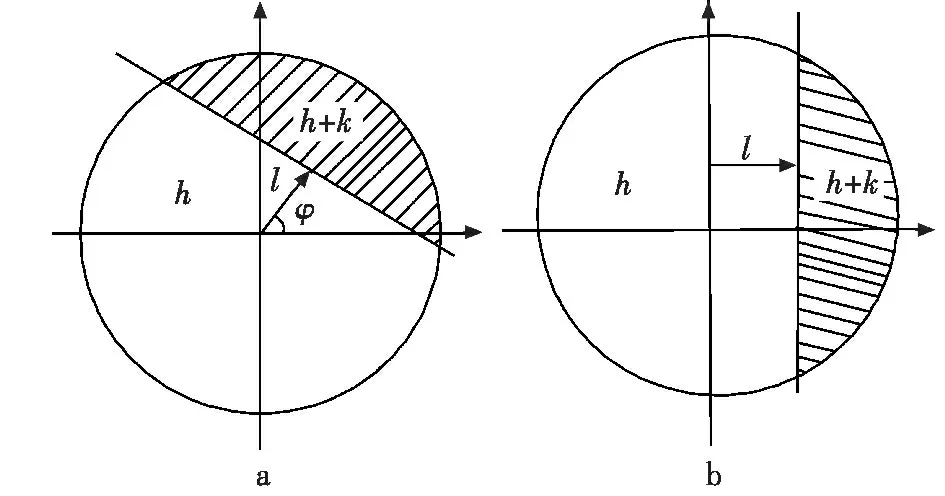
图1 理想平面亚像素边缘模型Fig.1 The ideal model of sub-pixel edge

表1 Zernike 径向多项式RnmTable 1 Zernike radial polynomials Rnm

表2 Zernike 矩的复数域多项式VnmTable 2 Complex domain polynomial of Zernike moments Vnm
在单位圆内,由Zernike 矩定义和图1b 中的阶跃边缘模型可以求得
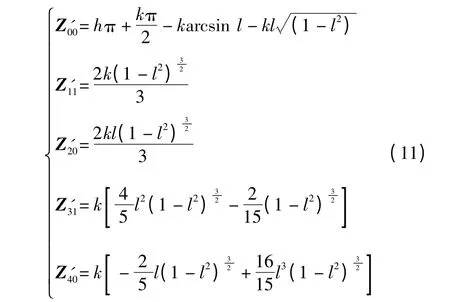
解Z20' 和Z40' 的方程可得
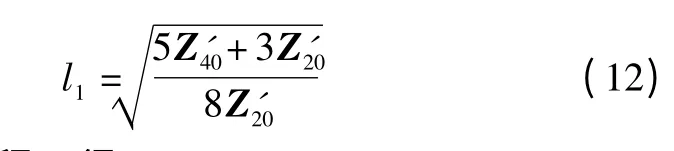
解Z11' 和Z31'的方程可得

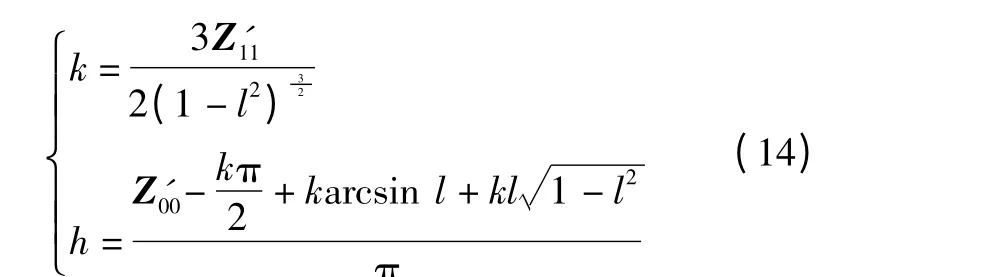
由式(10)可知
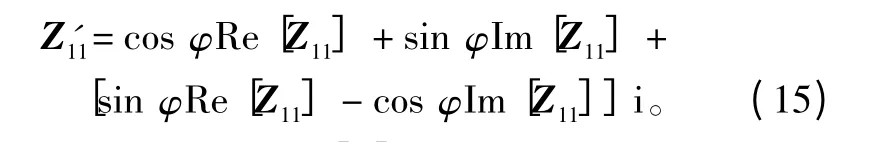
由图1 可以看出,Im[Z11']为关于y 的奇函数,因此Im[Z11']=sin φRe[Z11]-cos φIm[Z11]=0,故
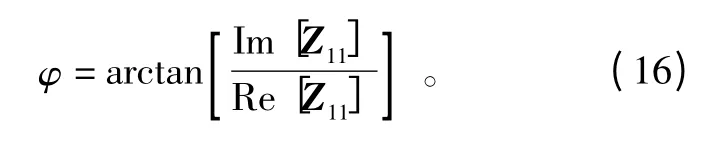
至此,平面亚像素阶跃边缘模型的4 个参数已经全部确定,由图1 可得,基于Zernike 矩的亚像素边缘检测式为
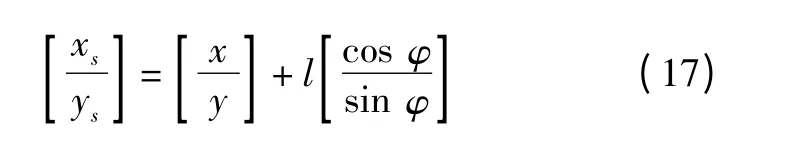
式中:(xs,ys)为亚像素坐标;(x,y)为图1 中的原点坐标。若Zernike 模板大小为N×N,则式(17)可以改写为
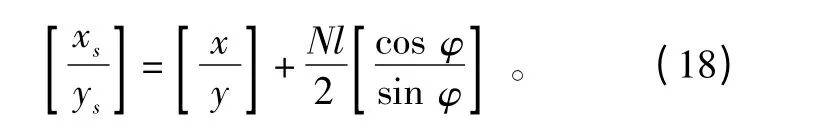
2.3 7 ×7 模板设计
为了进一步提高边缘检测精度,本文在文献[7 -8]提出的5 ×5 模板的基础上提出了7 ×7 模板,并将Z00,Z11,Z20的模板系数扩展到了Z00,Z11,Z20,Z31,Z40,Zernike 矩的7 ×7 模板如图2 所示。
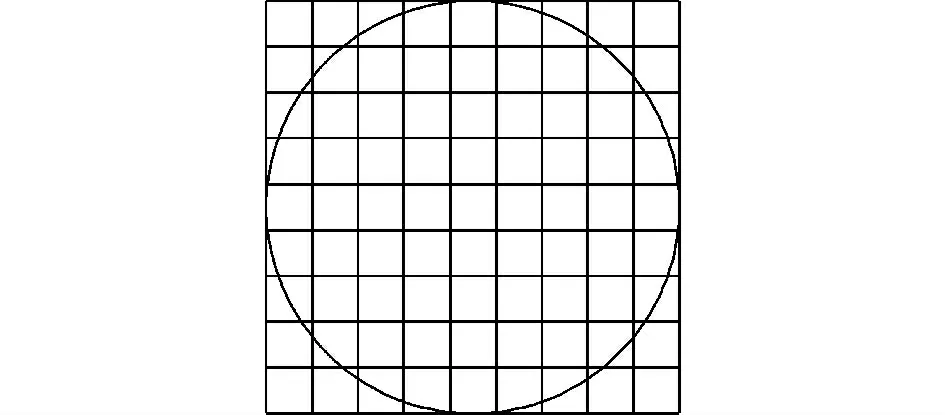
图2 Zernike 矩的7 ×7 模板Fig.2 The mask of size 7 ×7
在单位圆内,不同区域像素灰度为常数,因此,式(8)可以改写为
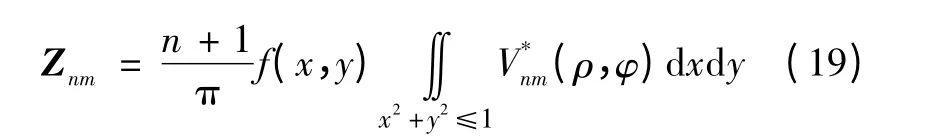
为了实现Zernike 矩的快速计算,定义Znm的模板为,由式(8)可知,将模板Mnm在图像上移动,与模板覆盖下的子图进行卷积运算,即可得到图像的Zernike 矩。
3 多尺度模极大值亚像素边缘检测算法
在对图像进行多尺度分解时,随着尺度的增大,图像会变得更加平滑,边缘的定位精度会变得更差,而另一方面,图像的信噪比会提高,抗噪能力会增强。因此,如果用大尺度来抑制信号的噪声,而用小尺度来提高边缘的定位精度,将会极大地提高边缘检测的效果,在此基础上,再用改进后的Zernike 矩算子对图像进行进一步的亚像素边缘提取。根据以上分析,设计多尺度模极大值亚像素边缘检测算法步骤如下所述。
1)选择一个合适的小波基函数。文献[9]中指出小波基的选取应遵循3 个原则:
①边缘在图像中表现为高频信号,因此滤波器应当是高通滤波器;
②检测边缘的小波应当是奇函数;
③小波函数应当是窗口函数,最好是紧支窗口。实际上,上述的3 条准则是小波函数的必要条件。而文献[10]于1992 年将3 次B 样条函数作为小波函数运用在边缘检测中取得了很好的效果,因此,本文采用3 次B 样条函数作为小波函数。
2)利用选取的小波函数对图像进行多层分解,本文选取分解层数J=3。
3)利用小波模极大值原理对各层进行单尺度边缘检测,计算模极大值Es(x,y)和幅角As(x,y),设置阈值Et,当Es(x,y)>Et,认为Es(x,y)为边缘信息。
4)将尺度为s 的边缘Es的每一像素点(x,y)与s-1 尺度上对应的3×3 邻域共9 个点进行比较,将模值和幅角相近的点确定为s-1 尺度的边缘信息Es-1(x,y),并将s-1 尺度上的其他边缘信息舍弃,依次计算,当s=1 时就得到了边缘图像E1(x,y)。
5)计算7×7 模板{M00,M11,M20,M31,M40},将模板在边缘图像上移动,并与模板覆盖下的子图进行卷积运算,从而得到边缘图像的Zernike 矩{Z00,Z11,Z20,Z31,Z40}。
6)根据2.2 节中介绍的公式计算平面亚像素阶跃边缘模型的距离l 与角度φ,将其代入式(18)中计算亚像素坐标。
4 实验结果与分析
为了验证算法的优越性,在Visual Studio2010 平台下利用C#语言设计了2 组对比实验。
第一组实验目的是为了提取图像边缘的亚像素坐标,为此,在电脑上人工生成一幅大小为128 ×128 的二值图像,如图3 所示,在图像中间插入了圆,圆心在(64,64),半径为40,亚像素边缘检测的部分结果如表3 所示。

图3 二值图像Fig.3 Binary image
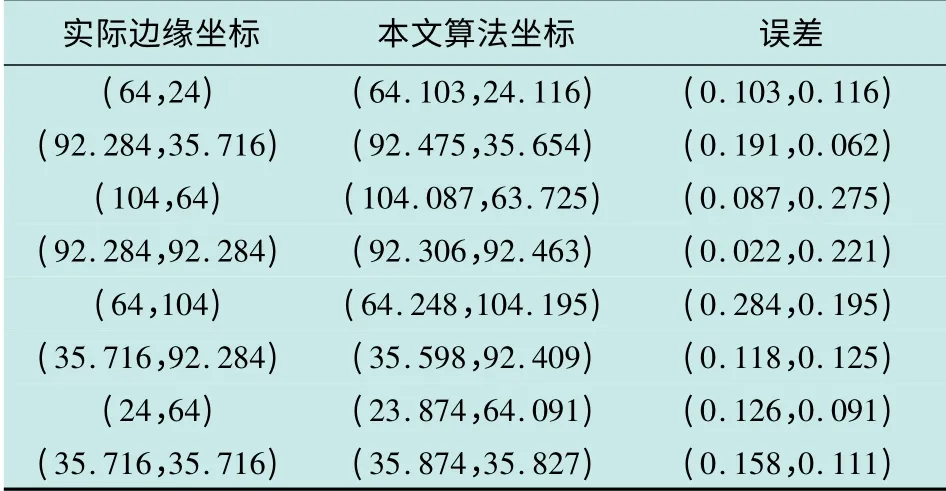
表3 三角形斜边亚像素检测Table 3 The triangle hypotenuse subpixel coordinate detection
从表3 中可以看出,边缘检测的最大误差为0.284像素,整体上误差较小,亚像素边缘定位精度较高。
为了测量某器件的几何参数,本文构建了一套基于图像的自动化测量系统,该系统通过对该器件的投影图像进行采集处理,达到测量的目的,为了满足可靠性好、精度高的测量要求,边缘检测算法必须具有高精确定位和强抗干扰性能的双重优势。
因此,为了验证算法的优越性能,本文对采集到的带有很强噪声的图像进行边缘检测,边缘检测结果如图4 所示。

图4 边缘检测结果对比Fig.4 Comparison of edge detection results
从图中可以看出,Sobel 算子和Prewitt 算子检测斜向阶跃边缘效果较好,Roberts 算子和LOG 算子精度较高,LOG 算子受噪声影响较Roberts 算子大,而Canny 算子虽然是基于精确定位和抗干扰的折衷推出的边缘检测算子,但在实际应用中检测效果也比较差,而基于改进小波变换和Zernike 矩的亚像素边缘检测算法抗噪能力强,且定位精度高。
5 结论
本文研究了一种基于改进小波变换和Zernike 矩的亚像素边缘检测算法,并进行了边缘检测实验。实验结果表明,该方法的抗噪能力比较强,且定位精度比较高,在提取效果上明显优于经典边缘检测算法,是一种稳定可靠的图像边缘检测算法。
[1] 金光远. 图像测量技术与系统[D]. 长春:吉林大学,2008.(JIN G Y.The design and realization for the measuring system based on image processing [D]. Changchun:Jilin University,2008.)
[2] 张铮,倪红霞,苑春苗,等.精通Matlab 数字图像处理与识别[M]. 北京:人民邮电出版社,2013. (ZHANG Z,NI H X,YUAN C M,et al.Proficient in Matlab digital image processing and recognition [M]. Beijing:Posts &Telecom Press,2013.)
[3] 孙红光,李勇. 基于双正交小波弱目标边缘提取方法[J].长春理工大学学报,2004,27(2):53-55. (SUN H G,LI Y.The method of faint object brim pick-up based on double orthogonal wavelet[J].Journal of Changchun University of Science and Technology,2004,27(2):53-55.)
[4] TELLO A M,LÓPEZ-MARTIÍNEZ C,MALLORQUÍ J J,et al.Edge enhancement algorithm based on the wavelet transform for automatic edge detection in SAR images[J].IEEE Transactions on Geoscience and Remote Sensing,2011,49(1):222-235.
[5] QIAO N S,TANG J.Study of edge detection of printed circuit board photoelectric image based on multi-scale wavelet transform[J]. Advanced Materials Research,2012,542:850-853.
[6] WEI B Z,ZHAO Z M.A sub-pixel edge detection algorithm based on Zernike moments[J].The Imaging Science Journal,2013,61(5):436-446.
[7] GHOSAL S,MEHROTRA R.Detection of composite edges[J].IEEE Transactions on Image Processing,1994,3(1):14-25.
[8] GHOSAL S,MEHROTRA R.Orthogonal moment operators for subpixel edge detection[J].Pattern Recognition,1993,26(2):295-306.
[9] 张宏群,张雪,肖旺新.小波变换的自适应阈值图像边缘检测方法[J].红外与激光工程,2003,32(1):32-36.(ZHANG H Q,ZHANG X,XIAO W X.Adaptive thresholds edge detection for image based on wavelet transform[J].Infrared and Laser Engineering,2003,32(1):32-36.)
[10] MALLAT S,ZHONG S G.Characterization of signals from multiscales edges[J].IEEE Transaction on Pattern Analysis and Machine Intelligence,1992,14(7):710-732.

