基于RELAX 算法的飞机油耗性能估计方法

刘家学， 马 涛， 陈静杰

(中国民航大学航空自动化学院，天津 300300)

0 引言

2013 年，我国民航业运输飞机起降731．5 万架次，运输周转量达671．7 亿吨千米，航空煤油消耗近2000万吨，碳排放量近6200 万吨［1］，运输飞机燃油成本目前已经占到航空公司运行成本的60%以上［2］。对航空运输业而言，良好的油耗性能同时也意味着较低的运营成本和碳排放量，航空公司在运力调配上更为关注机型的油耗性能指标评估。因此，利用实际飞行数据建立机型油耗性能模型并提取指标参数越来越引起业界的关注和重视。目前关于飞机油耗性能的模型中，文献［3］使用了神经网络的方法从飞机水平面运动、加速度、风向风速、倾斜角、纵向加速度等方面估计计算飞机瞬时燃油流量，偏重微观分析;文献［4］侧重于从效率角度评估航线运输，提出了优化飞机运行航路、改善机务维修方法、提高飞行操作能力等方法来提高飞机燃油效率，偏重于管理科学领域;文献［5］综述了飞机燃油消耗中可用的几类机器学习模型，包括使用线性回归、模型树、MLP 多层感知、SVM 支持向量机、自组织映射与Hopfield 神经网络等，并分析了几类方法各自的特点。关于飞机飞行整体油耗性能评估领域研究较少，而按照飞行小时与飞行千米评估飞机油耗性能应区分多个运行模式，不同模式表现不同的指标模型，区分模型需要一种合适的分离理论与估计方法。

松弛谱估计(RELAX)算法是一种信号分离算法，通过对信号分量的反复迭代估计信号参数。算法在变换域中运算，不改变信号的相对强度，信号分量在整体范围内表现相似特性，容易分离信号，但无法很好地估计不同时间呈现不同模式的混合信号［5］，基于广义内积(GIP)的非一致性检测(NHD)方法能够检测出信号分量的界限。针对不同时间区间上不同信号强度作用这个特性进行模式区分。

1 飞机油耗性能指标模型

民航飞机飞行主要分为起飞爬升段，空中巡航段与下降进近段3 个阶段，各段的油耗性能指标相差迥异，如图1 所示。

图1 Trent700 发动机典型燃油流量曲线Fig．1 Typical fuel flow chart of Trent700 aero engine

起飞爬升阶段总体燃油流量平均处于高值震荡区间。3000 s 后进入巡航阶段，燃油流量趋于平稳，均值相比爬升段减小明显;在保持巡航阶段基本平稳燃油流量后飞机进入下降阶段，下降段燃油流量呈现低值震荡。3 段在燃油流量分布上十分明显。设起飞爬升段、巡航飞行段、下降进近段飞行油耗指标样本集为{ycl，ycr，yde}，ycl＞ycr＞yde，若按照飞行距离分类有如下的两个特性。

1)飞机在本场起降训练或近场调机等短程航线飞行时，多处于爬升-下降或爬升-低高度巡航-下降两种模式。两种模式中起飞爬升段距离占飞行全程的绝大部分，表现在油耗指标上则ycl占据全程油耗指标的主导地位，小部分的ycr与yde无法抵消影响，总体指标很高。若根据能量守恒，短程航线中，爬升段的主导使飞机动能源源不断转化为势能，同时还要保证一定的分型速度产生足够升力。如图2 所示，地速与高度的快速增加使对应动能与势能都在提升，表现在油耗指标水平平均较高。

2)随着飞行距离的增加，飞机巡航阶段所占比重逐步加大。表现在油耗上ycr在3 段指标中所占比例也逐步加大，成为全程航段的主导油耗指标。如图2所示，在巡航期间，飞机动能与势能基本保持不变，不产生额外的转化关系，油耗指标ycr稳定偏小。此时可认为随着巡航距离增加时，占据主导的ycr不断中和ycl与yde的高低指标影响，使整体指标回归平稳，回归以指数形式渐渐逼近飞机最佳油耗指标，并且可以以距离为界分类油耗性能模式。

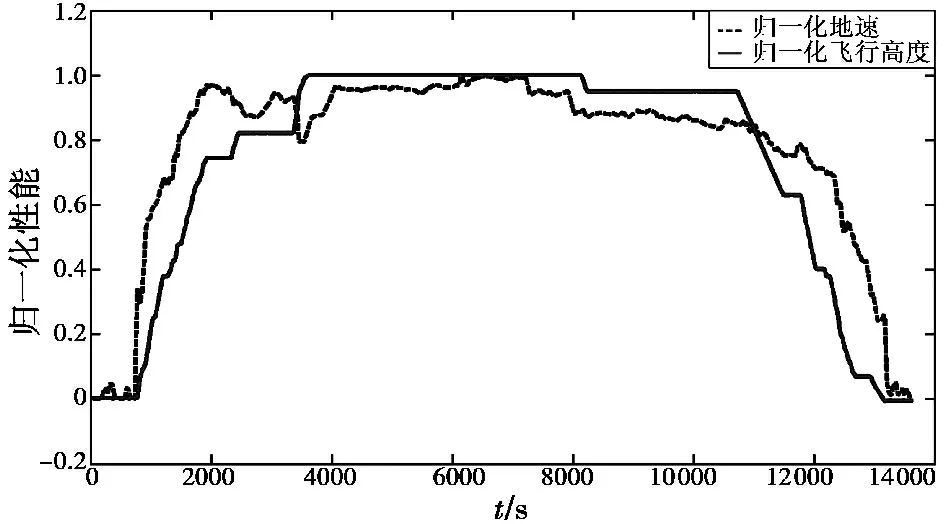
图2 某航段飞行高度与地速归一化曲线Fig．2 Normalized flight altitude and ground speed diagram

在航空公司指标评价体系中，飞机千米油耗yfkm多用来测算某机型与机队本身燃油利用效率，本文使用此指标评价上述指标模型较为准确。图3 所示为某飞机千米油耗与飞行距离的样本采样图，可看到随着距离增加，千米油耗yfkm递减，递减趋势明显呈现不同模式。指数下降型函数可以有效地描述这一递减过程，并且针对不同下降模式有着良好的参数描述。

模型为

式中:Ki表示指数递减项系数;n 代表主衰减分量个数，根据上述分析，n=2，分类两种模式;λi表示趋势变化实指数，根据回归趋势从大到小缓慢逼近且两种模式相差很大的特点，认为λ2＜λ1＜0;C 为常数项，代表当飞行距离x 趋近于无穷时油耗性能回归的极限值;en代表噪声信号即在其他因素作用下的油耗性能参数的噪声起伏。通过不同的实指数与衰减系数搭配固定油耗常数可以估计某机型的油耗指标。

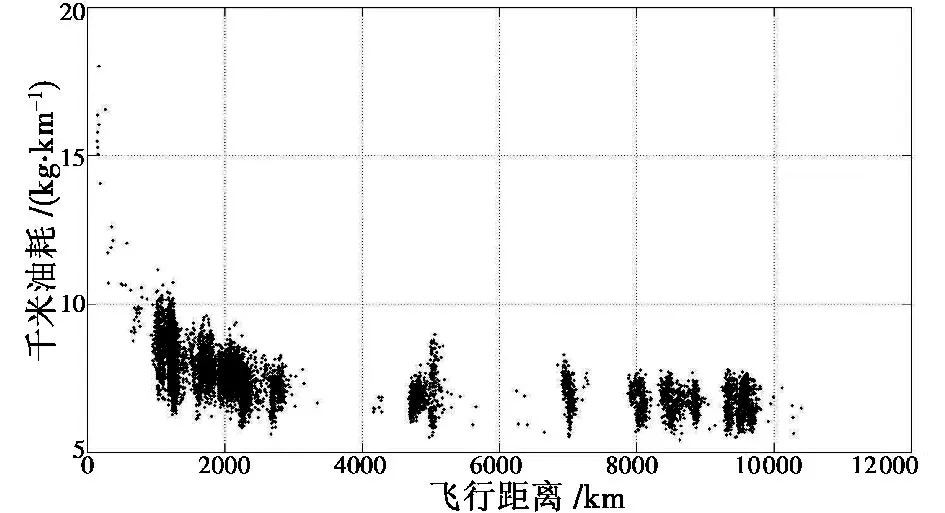
图3 A330 飞机飞行距离与千米油耗数据Fig．3 A330 flight distance vs fuel mileage

2 油耗模型的参数估计

根据收集到的油耗样本参数相应的飞行距离数据，数据分布与航线航路距离吻合，采样间隔并不平均，在某些区间范围内采样点比较分散，需要对传统的RELAX 算法进行一定的算法适应改变。因为模型无法采用FFT 方法进行运算，本文采用RELAX 算法的信号分离与参数迭代的思想进行运算。

根据距离油耗性能指标模型

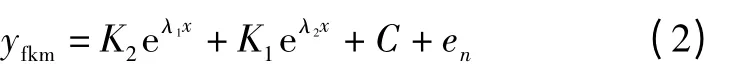
取

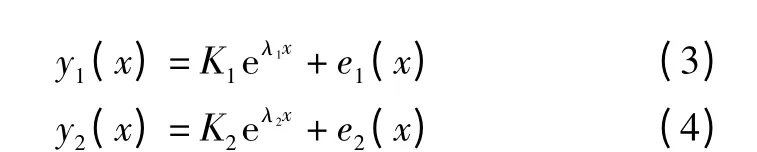
定义y1(x)为弱目标信号，y2(x)为强目标信号，不妨假设当距离x 增大到3 倍的距离常数，即x ＞3λ-1i 时，可认为信号已衰减完毕。估计时确定初始常数信号值，从弱目标信号到强目标信号，利用差分得到修正常数信号，整体不断交叉迭代修正所有分量信号，直到达到收敛条件为止。具体算法过程如下所述。

1)设定迭代次数，迭代次数应随着信号信噪比增加而减小，为了尽量达到良好性能，可取迭代次数n =100。并初始化常数信号，因为可能出现的噪声干扰信号，无法准确得知当飞行距离x 趋向于无穷时油耗性能常数C0的值，故取信号后部平均，根据噪声大小可动态选取平均值范围，一般认为后5%区间项均值作为初始C^0较为合适。设z1i为去除初始常数分量后的信号，对于每点信号yi有

2)进行弱分量与强分量的分层，分层原理借鉴了空时信号自适应处理中常用的非均匀检测(NHD)中广义内积(GIP)的方法。GIP 可以计算信号的马氏距离，分类不同信号的作用区间［6］。对z1i信号做相邻点差分，形成新的序列s，并且将新序列进行长度为K的多点分层形成序列R^。通过GIP 后的数据GIP(x)可明显看出信号中两种样本集的相似度差异。计算GIP 的变异系数，根据变异系数大小取平均值与系数标准差组合进行样本选取判断。

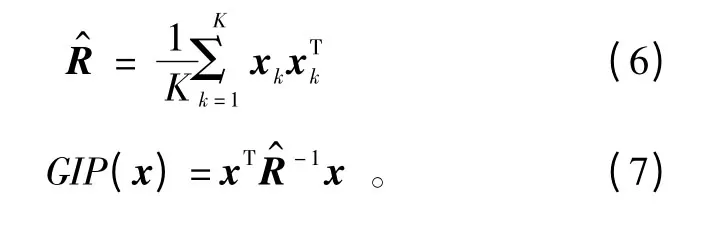
在样本选取界定范围时需要考虑噪声影响，在有噪声信号附加下GIP 值会在同频率处出现抖动，影响样本容量的选取，此时，可考虑使用二次GIP 运算或GIP 性能改进算法等类似滤波算法［7］，再一次细化可用信号区间，在确定后的区间内进行参数估计［8-9］。

样本的NHD 分类如图4 所示。

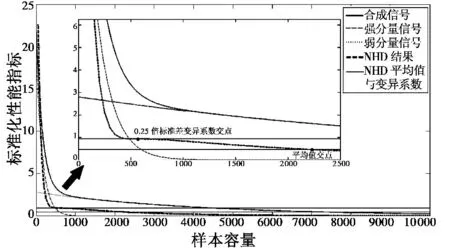
图4 样本的NHD 分类Fig．4 NHD classification of the sample

3)先在弱分量区间进行参数估计，使用差分方法来平均化消除噪声信号，并且考虑采样点的非周期性，对于差分采用每两点组合方式，共C2N 种，可得

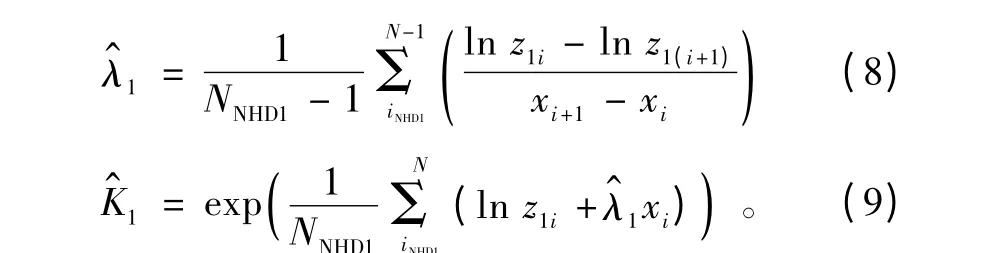
4)用原始信号减去已估计出的弱信号分量区间形成新的信号，并在强分量区间进行参数估计，可得

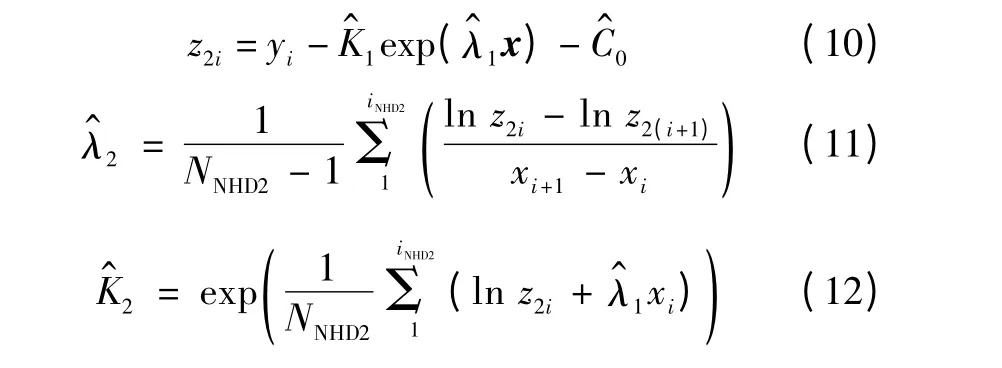
式中，iNHD1，iNHD2，NNHD1，NNHD2分别为对弱信号和强信号使用GIP 计算后确定的数据分界点和数据量。

5)设ej为误差向量，每点数据为xj，则

使用该误差向量的Frobenius 范数‖E‖F与门限值ε 进行参数估计结果的评估，若在n 次迭代过程中各参数估计结果的变化量低于ε，并且此时‖E‖F处于多次迭代过程的极小值区间，即可认为已达到“实际收敛”。

6)从估计出的各参数出发重新估计常数项C，去除估计信号后可再做一次GIP 运算得到新的iNHD3与NNHD3，挑选适合重新计算常数C 的区间，即

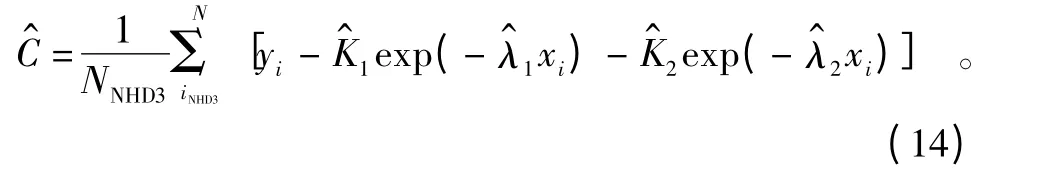
3 实际数据验证分析

验证算法采用两种方式进行:一种方式使用固定信号加油耗指标偏移噪声信号，噪声为高斯白噪声，信噪比步进5 dB，区间［-20 dB，20 dB］，再考虑一种信噪比无穷大时即没有噪声情况，评估考察算法误差的最佳性能，噪声信号叠加于所有飞行距离;另一种方式采用实际数据进行，采集了某航空公司2012 年10 月至2013 年8 月A330 飞机飞行千米油耗样本共8430项，对所有的样本进行原始点分布估计，使用本文方法进行仿真验证。

3．1 算法的噪声运算性能

使用标准信号作为固定信号加噪声影响验证此方法的通用性，对给定的最小信噪比RS，N，白噪声en～N(0，σ2)，标准差σ=K1e-3×10(-RS，N/20)。在不同SNR条件下各参数50 组估计平均值与克拉美-劳(CRB)对比如图5 所示。

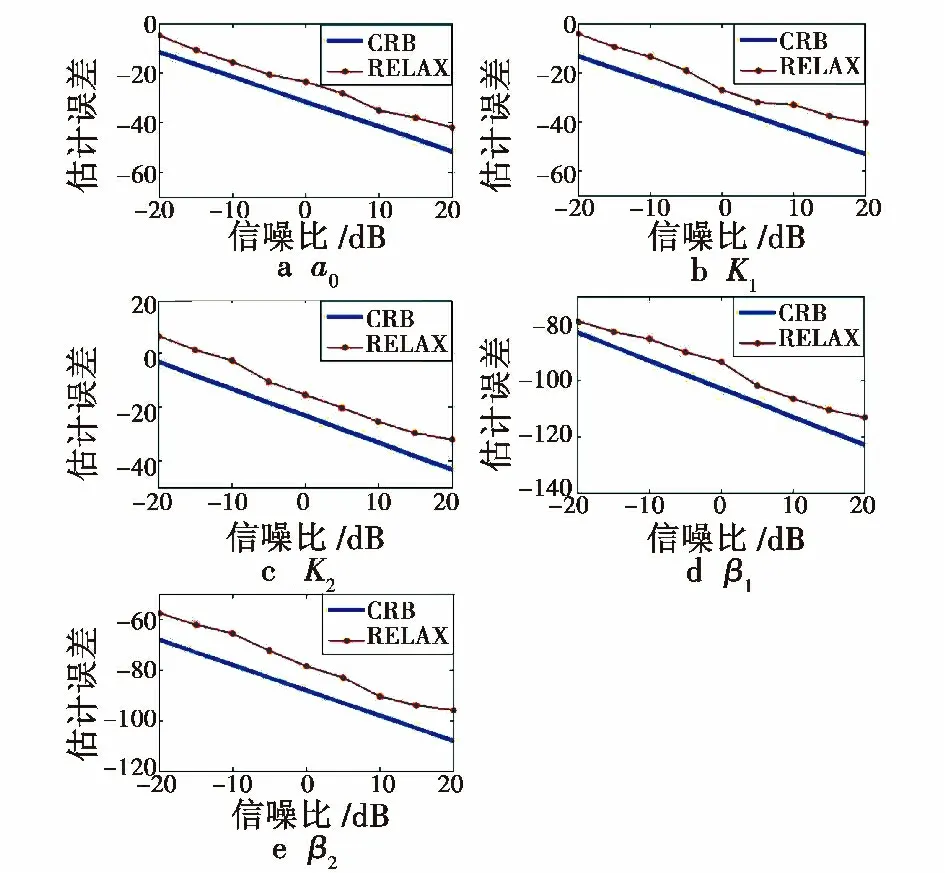
图5 参数估计精度与CRB 对比图Fig．5 Parameter estimation precision and CRB under the condition of standard signal

从图5 可看出，估计性能相对CRB 持续下降，算法效果显著，从50 组平均均方根误差与CRB 对比亦可看出上述关系，如图6 所示。

由图5、图6 可看出，算法的运算性能可以在不同信噪比条件下很好地估计出模型的各参数，在强噪声环境下，因为多次迭代和GIP 的使用，也可以很好地排除噪声的影响，逼近最佳性能。

当信号为理想形式即不叠加噪声时，算法收敛速度平滑减慢，震荡逼近正确信号形式，图7 所示为理想信号条件下误差均方根在100 次迭代后震荡收敛到原信号值，初始参数取值如表1 原始信号估计值，最佳收敛性能‖E‖F=0．0091。

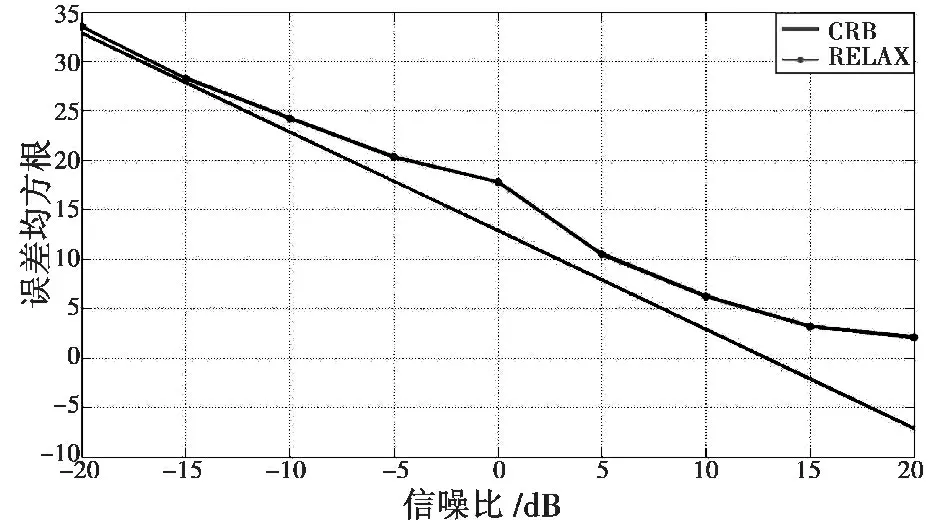
图6 不同信噪比下误差均方根与CRB 对比Fig 6 RMSE under various SNR comparied with CRB

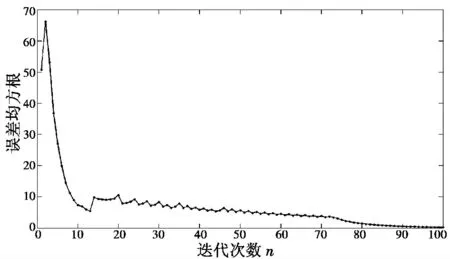
图7 理想信号条件下迭代次数与误差均方根变化趋势Fig．7 The RMSE trends under constant iteration

3．2 飞行数据试验结果

如图3 所示，A330 飞机所飞航段跨越了短中长各个阶段，从200 ～10000 km 均有涉及，总体符合前文模型所预示结果，其数据偏差似噪声扰动，并且噪声功率较强，使用本文方法在经过300 次迭代运算后，选取误差均方最小值点。各参数计算结果如图8 与表1 所示。

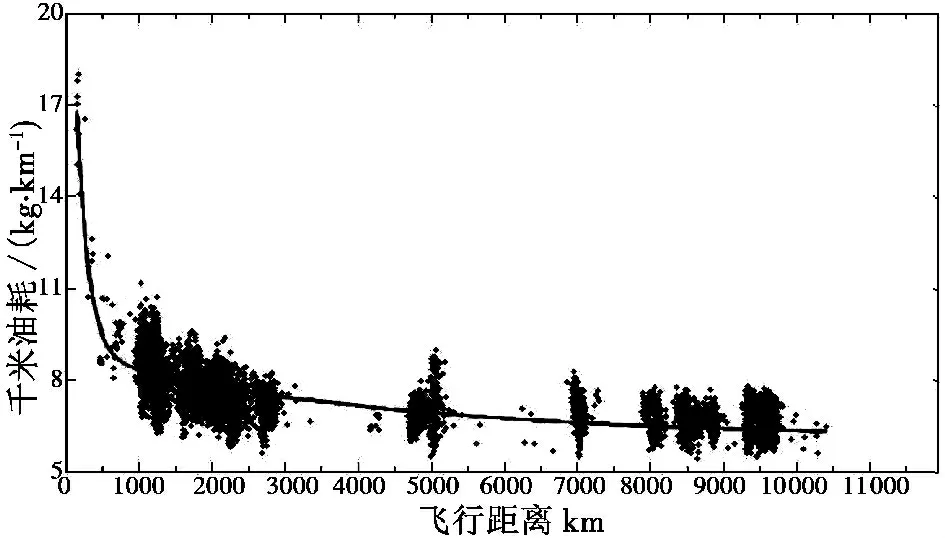
图8 A330 飞机8429 组数据实验结果Fig．8 8429 set of simulation data of A330

对所有原始数据进行128 点交叉平均采样处理，迭代100 次后可满足所有收敛条件，数据趋于平滑，平滑噪声影响后进行估计，两者估计参数与变化百分比计算结果如表1 所示。

表1 参数估计结果Table 1 Result of parameter estimation

可以看出，当数据进行多点平均后，对于原始参数变化没有超出10%，说明算法在平均化输入后亦可得到较好的结果。

3．3 模型仿真结果推论

根据表1 平均后的数据计算结果，A330 飞机的油耗性能参数(单位为kg/km)及两个距离常数(单位为km)分别为min{yA330}= 6． 21，max{yA330}= 6． 21 +20．01 + 2．7 = 28．92，RA330，1= 1/0． 006 2 = 161．29，RA330，2=1/0．000 252 =3 968．3。指数衰减项衰减到离性能参数下限值10%的飞行距离(单位为km)分别为rA330，1= ln(10 ×20． 01/6． 21)× RA330，1=560，rA330，2=ln(10 ×2．7/6．21)×RA330，2=5832。故根据模型数据可推论，A330 飞机在航段距离小于560 km 时起飞带来的油耗高性能指标占据主导因素，此距离范围内选择该机型执行航线油耗性能指标较高。在5832 km 后可认为已达到理想油耗性能，大于此距离时飞机可以忽略起飞段高指标影响，油耗性能指标平稳偏低。

4 总结

油耗指标模型是航空公司评价燃油消耗与节能减排的重要评估手段，基于RELAX 思想的信号分离，迭代估计算法具有一定的抗噪性能以及通用性，进行油耗模型的精细化估计是可行的，为航空公司监控机队油耗水平等方面提供一个可行的方法，也可为航线机型选型提供一定的参考。

［1］ 中国民用航空局．2013 中国民航业发展公报［EB/OL］．(2013-06-01)． http://www． caac． gov． cn/I1/K3/201406/P020140623612275082363．pdf．(CAAC．Civil aviation development statistical bulletin of China in 2013［EB/OL］．trol，2006，13(3):11-14，28．)(2013-06-01)． http://www． caac． gov． cn/I1/K3/201406/P0201406236 12275082363．pdf．)

［2］ 孙宏，李峰，黎青松．民用航空航班直接运行成本测算分析［J］．交通运输工程与信息学报，2007，5(1):1-5．(SUN H，LI F，LI Q S．Research of civil aviation flight direct operating cost［J］． Journal of Transportation Engineering and Information，2007，5(1):1-5．)

［3］ 刘婧．基于飞行数据分析的飞机燃油估计模型［D］．南京:南京航空航天大学，2010．(LIU J．The aircraft fuel estimation model based on flight data analysis［D］． Nanjing:Nanjing University of Aeronautics and Astronautics，2010．)

［4］ 罗杰．航空运输燃油效率影响因素分析［D］．广汉:中国民用航空飞行学院，2010．(LUO J．Analysis of the factors affecting fuel efficiency of air transportation［D］． Guanghan:Civil Aviation Flight University of China，2010．)

［5］ LI G Z． Machine learning in fuel consumption prediction of aircraft［C］//The 9th IEEE International Conference on Cognitive Informatics (ICCI)，2010:358-363．

［6］ LI J，PETRE S． Efficient mixed-spectrum estimation with applications to target feature extraction［J］． IEEE Transactions on Signal Processing，1996，44(2):281-295．

［7］ MELVIN W L，WICKS M C． Improving practical spacetime adaptive radar［C］//IEEE National Radar Conference，Syracuse，New York，USA，1997:48-53．

［8］ 郭佳佳，廖桂生，杨志伟，等． 利用广义内积值迭代加权的空时协方差矩阵估计方法［J］．电子与信息学报，2014，36(2):422-427． (GUO J J，LIAO G S，YANG Z W，et al． Iterative weighted covariance matrix estimation method for STAP based on generalized inner products［J］． Journal of Electronics ＆ Information Technology，2014，36(2):422-427．)

［9］ 李艳，肖怀铁，付强．Radon-Wigner 变换改进算法在多目标分辨及参数估计中的应用［J］．电光与控制，2006，13(3):11-14，28． (LI Y，XIAO H T，FU Q． Application of improved Radon-Wigner transform in multi-target resolving and parameter estimation［J］． Electronics Optics ＆ Con-