灰色线性幂函数曲线模型在故障预报中的应用

黄 莹

(1．武警工程大学信息工程系，西安 710086; 2．西安交通大学制造系统工程国家重点实验室，西安 710049)

0 引言

武器系统的故障预报是提高系统可靠性、避免事故发生的有效途径，是进行武器系统管理的基础。由于武器系统故障发生及其发展过程具有不确定因素，且系统处于部分信息已知、部分信息未知的“贫”信息系统的范畴，而灰色系统理论专门针对“小样本、贫信息”进行建模分析［1］，在很多复杂系统中应用非常广泛［2-8］。因此将武器系统视为一个灰色系统具有较强的适用性，可以根据系统过去和现在的监测信息对未来的状态进行预测，进而判断是否会发生故障。

GM(1，1)模型是灰色系统理论常用的模型，利用GM(1，1)模型进行数列预测，对单调非负数列模拟效果很好［2］，但对摆动序列效果则不好，很难反映序列的随机波动变化［3］。然而，武器系统的故障数据序列时常呈现摆动特性，且振荡幅度较大，所以必须研究如何针对摆动数据序列建模，即研究GM(1，1)模型的改进方法。对于GM(1，1)模型的改进大致专注于两个方向:1)针对原始数据序列采取数学的方法进行序列变换使其满足GM(1，1)建模的条件［3-10］;2)对于背景值进行重构［11］。

对于波动性较强的灰色摆动序列进行建模的方法，其重点在于从根本上改变原始数据的波动性，使之满足建模的条件。虽然已有一些原始数据序列的变换方法［3-10］，但是都是基于不同的数据特点进行变换，对于武器系统故障数据的随机波动性还需进一步研究适应性更强的方法。

基于此，本文针对武器系统故障特征量存在摆动数据序列的特点，利用动态指数变换，使灰色摆动序列变换为具有一定灰指数律的单调增序列。通过建立灰色线性幂函数曲线模型——GIM(1)模型(Grey Linear Exponential Curve Model)，用一元线性回归的方法对模型参数进行辨识，最后再利用该模型预报故障。研究表明，GIM(1)模型不仅适用于灰指数律系统的分析建模，也适用于比指数律更复杂的线性律与幂指数律的耦合系统的分析建模，具有广泛的适用性。

1 经典GM(1，1)模型的建模机理

设原始数据序列为

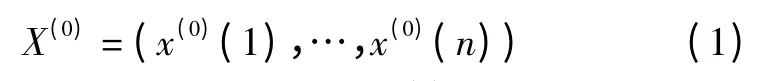
式中:x(0)(k ≥0)，k = 1，…，n;X(0)的一次累加(1-AGO)生成序列为X(1)=(x(1)(1)，…，x(1)(n))，X(1)的紧邻均值生成序列Z(1)= (z(1)(2)，z(1)(3)，…，z(1)(n))，其中

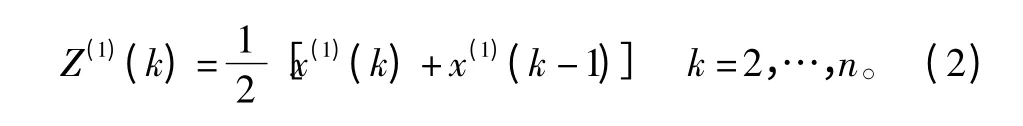
若a^=(a，b)T为参数列，且Y=(x(0)(2) x(0)(3) … x(0)(n))T，则GM(1，1)灰色微分方程(又称灰色方程的基本形式或差分形式)为

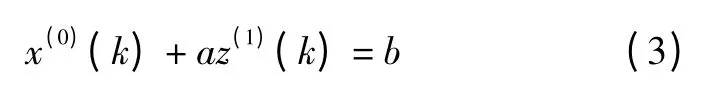
最小二乘估计参数列满足

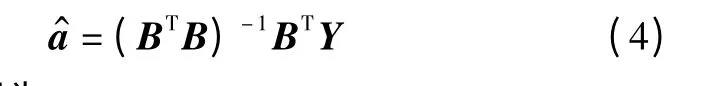
其白化微分方程为

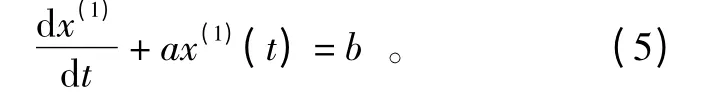
对应GM(1，1)灰色微分方程的时间响应序列为

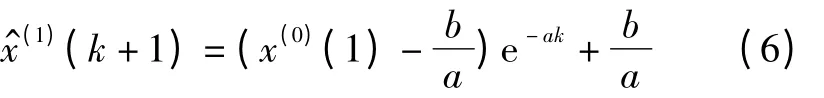
则其原始序列的模拟预测差分形式为

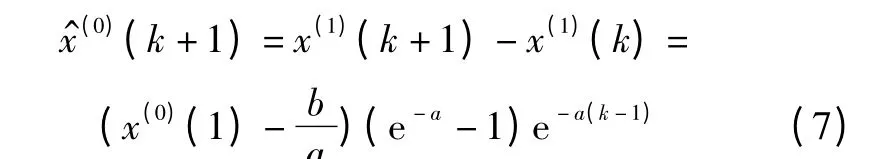
模型中:a 为发展系数;b 为灰色作用量。

2 GIM(1)模型

GIM(1)模型是由GM(1，1)派生的一种较新的灰色模型，定义其为灰色线性幂函数曲线模型。

建模方法:首先利用动态指数变换，使灰色摆动序列变换为具有一定灰指数律的单调增序列，然后建立GIM(1)模型。

2．1 灰色摆动序列的设定

设某系统形成的时间序列为X(t):X(1)，X(2)，…，X(n)，t=1，2，…，n。1)当X(2)/X(1)＞1，X(3)/X(2)＜1，…，且X(n)/X(1)＞1(＜1)，称其为具有增长(下降)趋势的灰色左摆动序列;2)当X(2)/X(1)＜1，X(3)/X(2)＞1，…，且X(n)/X(1)＜1(＞1)，称其为具有增长(下降)趋势的灰色右摆动序列。

本文研究具有增长趋势的灰色摆动序列。

2．2 灰色摆动序列的动态指数变换

本文给出一种新的动态摆动指数变换公式

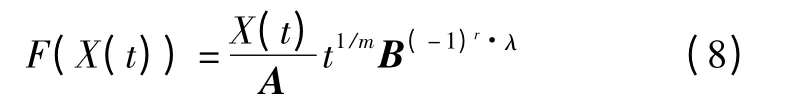
式中:A ＞0;m ＞0;B ＞0;r ＞0;λ ＞0。

2．3 灰色参数的赋值

参数一般依靠经验确定，但为了减少盲目性，根据系统分析经验给出如下两种赋值方法。

1)对灰色左摆动序列:r=t-1，A=(B-1)1/2。

2)对灰色右摆动序列:r=t，A=1 +B。m，λ，B 分别确定为

2．4 GIM(1)模型的建立

1)GIM(1)模型的白化微分方程形式为

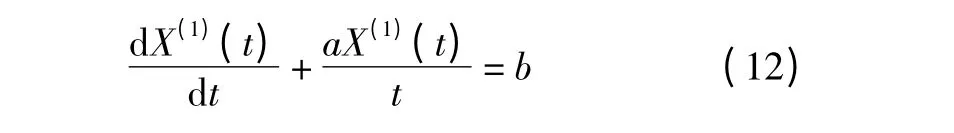
其通解为

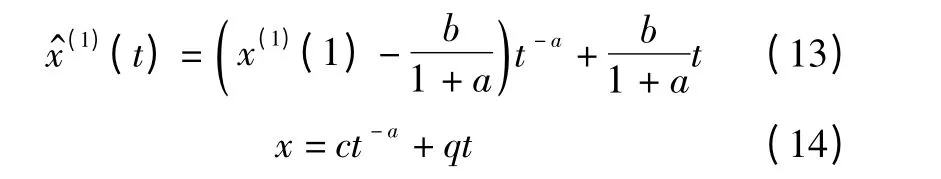
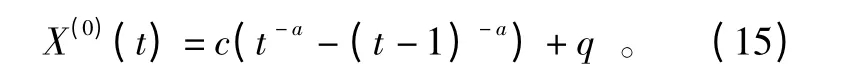
由上式可见，这是一个由幂函数与线性函数组成的复合函数，被定义为灰色线性幂函数曲线，简称GIM(1)。当a→+∞时，X(1)(t)→qt;当a→-∞时，X(1)(t)→+∞。

特殊地，当a=0 时，式(14)即蜕化为一元线性函数。因此可以说，一元线性函数是GIM(1)模型的特例。

2)GIM(1)模型参数辨识。

对于式(12)中的a，b，c，q，运用两次一元线性回归方法，分别求出a，b 的优化值。

对于式(12)，令

由于ΔX(1)(t)=X(1)(t)-X(1)(t -1)=X(0)(t)，当取Δ(t)=1 时，代入式(16)，得

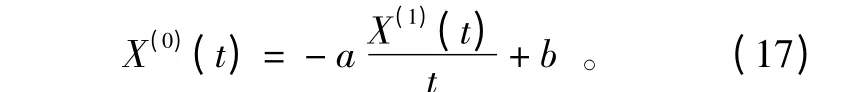
Wade：Yeah, Wade, Z. You can call me whatever you want. I’ll call you Sam.

显然这些公式均为一元线性回归方程，a，b，c，q 值均能方便而快捷地求出。

上述为灰色摆动序列GIM(1)动态摆动指数变换一元线性回归优化建模法。它不仅适用于灰指数律系统的分析建模，也适用于比指数律更复杂的线性律与幂指数律的耦合系统的分析建模。

3 GIM(1)改进优化灰色模型在武器故障预报中应用研究

3．1 对于一般性数据的处理

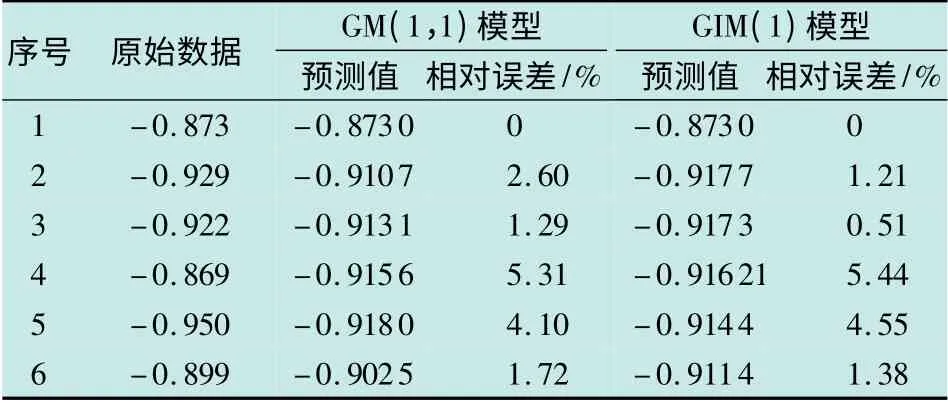
表1 光滑数据序列GM(1，1)和GIM(1)预测结果Table 1 The smooth data sequence prediction results of GM(1，1)＆ GIM(1)

从表1 中可以得出GIM(1)模型，同样适用于灰指数律系统的分析建模，当原始数据序列具有较好的光滑度时，能得到较满意的预测精度，其预测的精度与经典GM(1，1)模型预测的精度大体相同。

3．2 对于摆动性数据的处理

经计算得到摆动指数变换公式为

建模计算的结果见表2，用数列的后5 个数据进行预测的精度检验，结果如表3 所示。

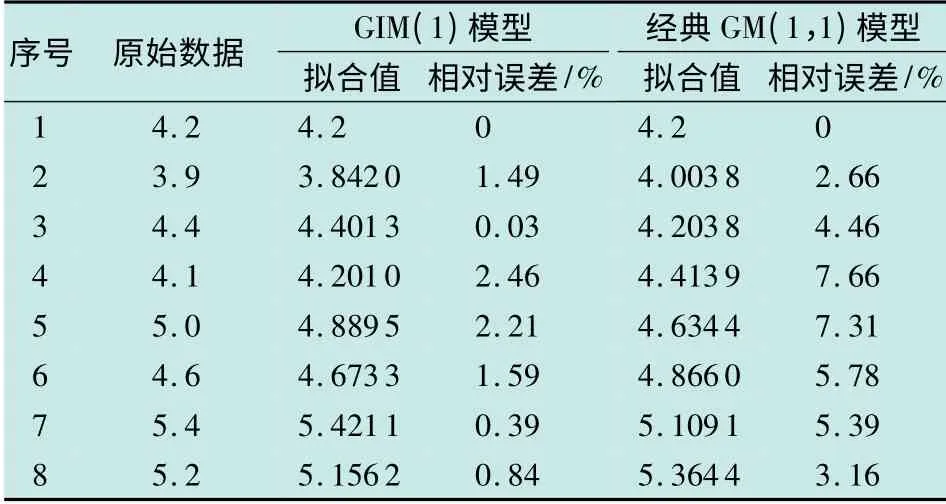
表2 摆动数据序列GIM(1)与经典GM(1，1)拟合精度比较Table 2 The swing data sequence fitting accuracy of GIM(1)and GM(1，1)

表3 摆动数据序列GIM(1)与经典GM(1，1)预测精度比较Table 3 The swing data sequence prediction accuracy of GIM(1)and GM(1，1)

从表2 和表3 中可以看出，对于具有摆动趋势，且具有线性律与幂指数律耦合性的序列，进行摆动序列的动态指数变换，然后建立GIM(1)模型，得到模型的拟合精度和预测精度都较经典的GM(1，1)模型高。

4 结束语

由于现代武器装备系统日趋复杂，使其表现出极其复杂的故障规律，对装备保障的要求也越来越高，因此，进行装备的预防性维修已经成为了部队保障战斗力的一个重要课题，进行故障预报掌握维修的主动权，对充分发挥装备的使用效能，提高战备完好率等方面具有重大意义。

本文在研究武器系统故障特征量和灰色系统理论的基础上，针对武器系统故障特征量存在灰色摆动序列的特点，研究建立了GIM(1)模型。其建模方法为:利用动态指数变换，使灰色摆动序列变换为具有一定灰指数律的单调增序列，然后建立GIM(1)模型。

本文验证了经典GM(1，1)模型比较适用于描述单调变化的过程，而GIM(1)模型不仅适用于灰指数律系统的分析建模，也适用于比指数律更复杂的线性律与幂指数律耦合系统的分析建模。当数据序列呈现摆动趋势且具有线性律与幂指数律时，用摆动处理结合GIM(1)模型将使模型的预测和拟合精度得到显著提高。

［1］ 邓聚龙．灰理论基础［M］．武汉:华中科技大学出版社，2002．(DENG J L． Grey theory［M］． Wuhan:Huazhong University of Science and Technology Press，2002．)

［2］ 王清朝．GM(1，1)模型在铁路装卸运输综合生产效率预测中的应用［J］．油气储运，2013，32(11):1198-1201．(WANG Q C．Application of GM (1，1)in comprehensive production efficiency prediction［J］．Oil ＆ Gas Storage and Transportation，2013，32(11):1198-1201．)

［3］ 仝蕊，申卯兴，任俊亮，等．基于反三角函数变换的振荡序列灰色预测模型研究［J］．统计与决策，2010(24):20-22．(TONG R，SHEN M X，REN J L，et al．The oscillatory sequence grey prediction model based on inverse trigonometric function transformation［J］．Statistics and Decision，2010(24):20-22．)

［4］ 刘思峰．灰色系统理论的产生与发展［J］．南京航空航天大学学报，2004，36(2):267-272．(LIU S F．Emergence and development of grey system theory and its forward trends［J］．Journal of Nanjing University of Aeronautics ＆ Astronautics，2004，36(2):267-272．)

［5］ 李小力，李言俊，张科．改进的灰色预测模型在导弹中的应用［J］．计算机仿真，2010，8:33-36，60．(LI X L，LI Y J，ZHANG K． Improved grey forecasting model of fault prediction in missile applications［J］．Computer Simulation，2010，8:33-36，60．)

［6］ 刘发全，职承杰．灰色预测GM(1，1)模型的一点改进［J］．数学的实践与认识，2005，35(11):11-15． (LIU F Q，ZHI C J． Improvement of grey prediction model GM(1，1)［J］．Mathematics in Practice and Theory，2005，35(11):11-15．)

［7］ 周俊，张鹏． 基于灰色预测的农业机器人GPS 导航系统硬故障隔离［J］．农业机械学报，2010，41(12):165-168，177． (ZHOU J，ZHANG P． Hard fault isolation of GPS navigation system based on gray prediction for agricultural robot［J］．Transactions of the Chinese Society for Agricultural Machinery，2010，41(12):165-168，177．)

［8］ 王奎民． 基于灰色预测的无人水下航行器目标跟踪［J］．自动化技术与应用，2013，32(12):1-4．(WANG K M．Moving target tracking based on grey prediction for unmanned underwater vehicle［J］．Techniques of Automation and Application，2013，32(12):1-4．)

［9］ 邓微，吴东伟，李文，等．基于灰色预测理论的频谱空洞特性分析研究［J］． 信息技术，2012(9):28-32． (DENG W，WU D W，LI W，et al． Research on spectrum hole in characteristics analysis based on gray-predictive-model［J］．Information Technology，2012(9):28-32．)

［10］ 曾祥艳，舒兰，蒋贵荣，等．基于三角模糊数序列的灰色预测模型［J］． 数学的实践与认识，2012，42(19):107-112．(ZENG X Y，SHU L，JIANG G R，et al． Grey prediction model based on triangular fuzzy number series［J］．Mathematics in Practice and Theory，2012，42(19):107-112．)

［11］ 刘乐，王洪国，王宝伟． 基于背景值构造方法的GM(1，1)模型优化［J］．统计与决策，2009(1):153-155．(LIU L，WANG H G，WANG B W．The GM(1，1)model optimization based on the structure method of background value［J］．Statistics and Decision，2009(1):153-155．)