基于X 射线脉冲星的月球卫星自主导航

姚 翔， 吴盘龙， 陈尚敏

(南京理工大学自动化学院，南京 210094)

0 引言

近年来，随着航天科技的飞速发展和对月球认识的深入，月球已成为人类进行深空探测的重要基础，月球探测成为世界航天的热点［1］。当前月球卫星主要依靠地面站进行遥控遥测，月球卫星与地面站距离较远，信号延迟大，月球背面不可见弧段等，且月球卫星上必须装备复杂而昂贵的测控和通信设备。因此，对月球卫星进行自主导航具有重要意义，一方面可以大大降低探测任务和地面支持的成本，另一方面有助提高月球卫星的生存能力［2-4］。

X 射线脉冲星导航(XNAV)是一种适合于深空探测的新兴天文自主导航技术，能够为近地轨道、深空和星际空间飞行的航天器提供位置、速度、时间和姿态等高精度导航信息［5-6］。XNAV 不与外界进行信息传输和交换，具有抗干扰能力强、可靠性高、适用范围广和误差不随时间积累的优点，发展潜力很大，在航天领域具有巨大的应用前景［7］。

本文提出一种基于X 射线脉冲星导航的月球卫星自主导航方法。结合月球卫星轨道动力学方程和脉冲星的量测信息，利用分段式定常系统(PWCS)的可观测性分析方法对导航系统进行可观测性分析，并采用航天领域广泛使用的扩展卡尔曼滤波(EKF)算法进行数据处理。最后，通过数学仿真，验证了该系统能够实现月球卫星的自主导航。

1 导航系统数学模型

1．1 月球卫星轨道动力学方程

选取历元(J2000．0)月心赤道惯性坐标系，月球卫星轨道动力学方程可以表示为［8］

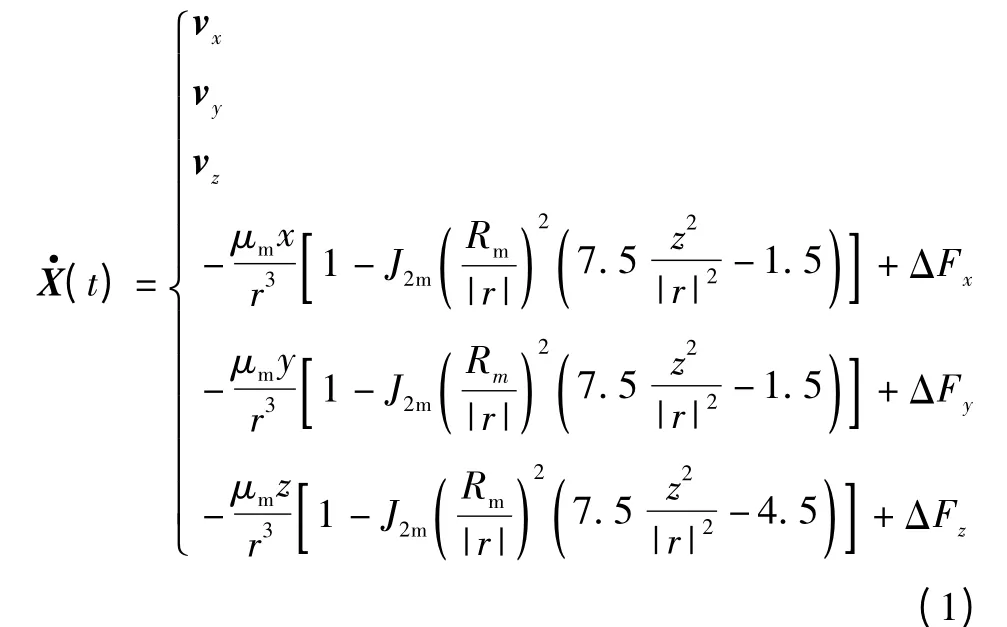
可简写为一般的状态方程

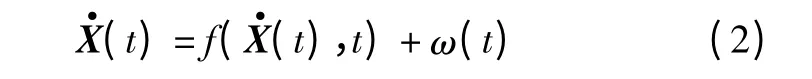
式中，X(t)=［x，y，z，vx，vy，vz］为状态变量，其中，x，y，z，vx，vy，vz分别表示3 个坐标轴所在方向航天器的位置与速度2 为航天器与月心的距离;μm=0．49028×1013m3/s2为月球引力常数;J2m=203．8×10-6为月球引力二阶带谐项系数;Rm为月球的平均半径;Fx，Fy，Fz表示航天器受到的摄动在x，y，z 3 个方向上的分量，包含月球的非球形因素;w(t)为等效的随机白噪声。

1．2 脉冲星导航量测方程

X 射线脉冲星导航系统的量测量是脉冲到达航天器与到达太阳系质心(SSB)的时间之差。脉冲到达航天器的时间通过航天器上的X 射线探测器观测得到，而到达SSB 时间是通过脉冲星钟模型预报得到的［9］。脉冲星导航基本原理如图1 所示。

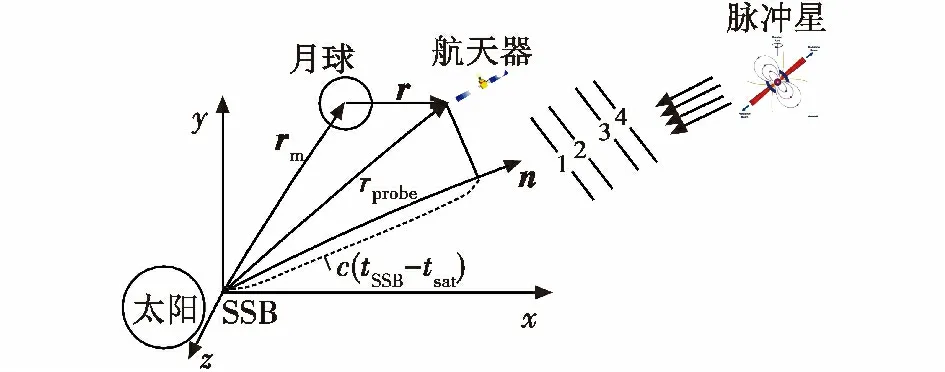
图1 脉冲星导航原理Fig．1 Geometric navigation principle based on X-ray pulsar

图中:tsat和tSSB分别为脉冲信号到达航天器和SSB的时间;r 为航天器相对月球的位置矢量;rm为月球相对SSB 的位置矢量;rsat=rm+r 为航天器相对太阳系质心的位置矢量;反映了rsat在脉冲星方向矢量n 上的投影。脉冲星的方向矢量为

式中，λ 和α 分别为SSB 坐标系下脉冲星的赤经和赤纬。

航天器测得的脉冲到达时间经过时间变换后，相对于太阳系质心的位置与时间差之间的关系可表示为

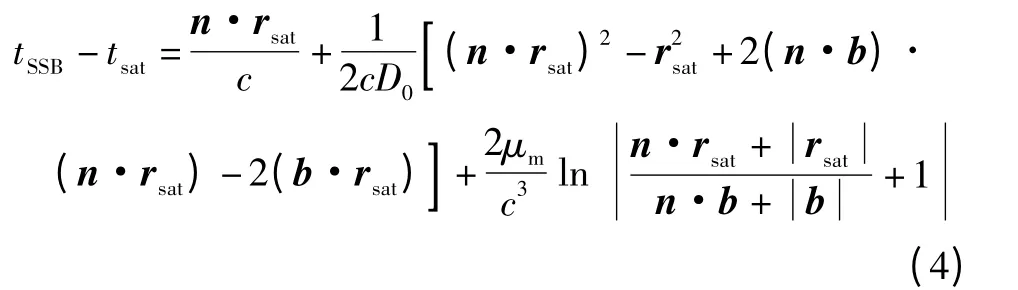
式中:c 为光速;b 为太阳系质心(SSB)相对太阳质心的位置矢量;D0为太阳质心与脉冲星之间的距离。式(4)右边开始第一项表示两个位置间简单的几何时间延迟，称之为Doppler 延迟;第二项是由时差效应引起的Roemer 延迟效应;最后一项是太阳引力场产生的光程弯曲所造成的太阳Shapiro 延迟效应。

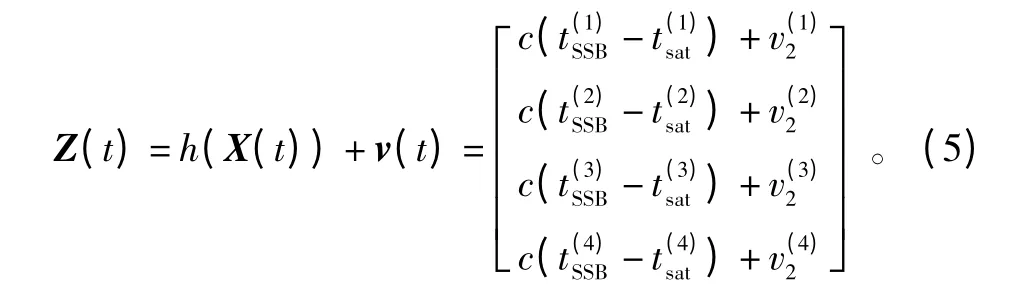
X 射线脉冲星导航精度主要取决于脉冲到达时间(TOA)TTOA的测量精度σTOA。而TTOA的测量精度σTOA又是由脉冲轮廓的信噪比(SNR)RS，N决定的［10］。X 射线脉冲星辐射信号的信噪比为信号光子数Np和噪声σN的比值，所示［11］为

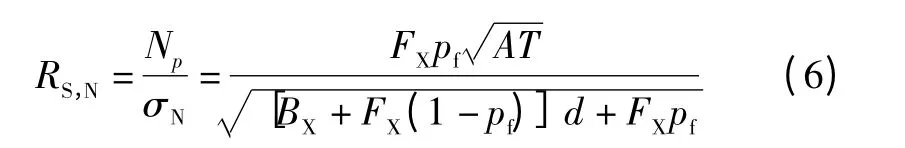
式中:BX为X 射线背景辐射流量，根据Naval 实验室的经验，一般取值为0．005 ph/(cm2·s-1);FX为X 射线辐射光子流量;pf为脉冲信号辐射相对脉冲星总辐射的比值;A 为探测器面积;T 为脉冲信号的观测时间;d 为脉冲宽度W 与脉冲周期P 的比值。

对于一个给定的观测，TTOA测量精度可通过脉冲宽度和脉冲信噪比确定，即

此精度表示基于单个观测的脉冲到达时间分辨率，一个TOA 量测可用于确定在视线方向上探测器到参考点之间的距离，距离测量精度为

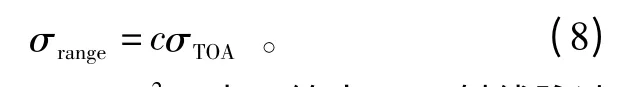
设置探测器面积A=1 m2。表1 给出了X 射线脉冲星的参数，表2 给出了4 颗脉冲星的距离观测精度随观测时间变化的关系。

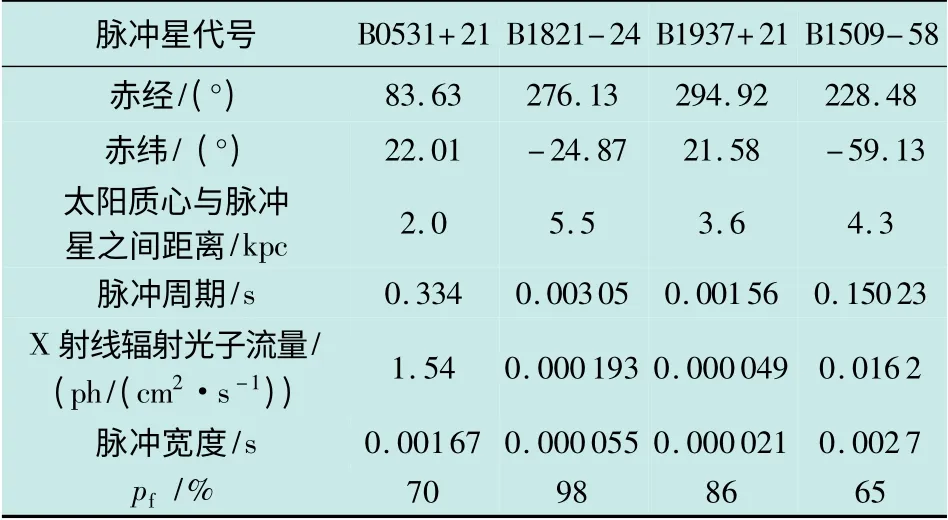
表1 X 射线脉冲星参数Table 1 Parameters of the X-ray pulsars

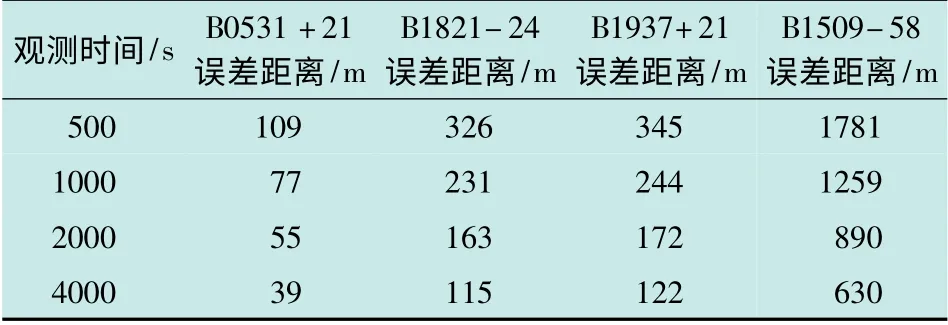
表2 距离观测精度随时间变化关系Table 2 Range measure accuracy with observation time

距离观测精度随时间变化情况如图2 所示。

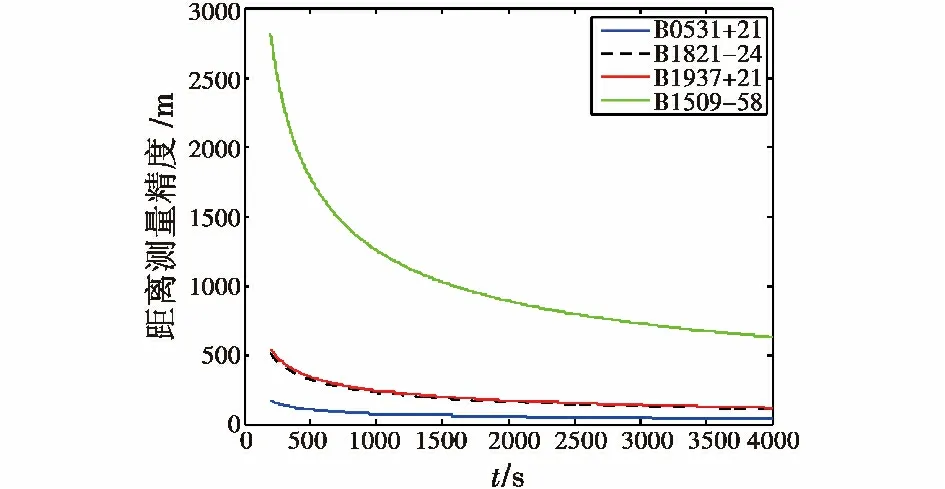
图2 距离观测精度随时间变化图Fig．2 The range measurement accuracy with the observation time

由图2 和表2 可知，观测时间越长，距离观测精度就越高。但是，累积时间越长会导致累积误差越大，那么导航系统误差就越大。

2 系统可观测性分析

在一个足够小的时间区间内，如果线性时变系统的系数矩阵变化量可以忽略不计，那么，在该时间区间内就可以把时变系统当作定常系统处理，则称这样的系统为PWCS，对其进行可观测分析的步骤和算法称为PWCS 可观测性分析方法［12-13］。

对于离散型系统

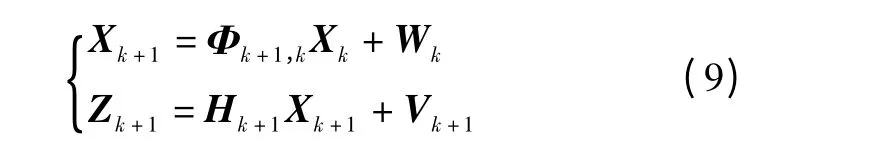
式中:

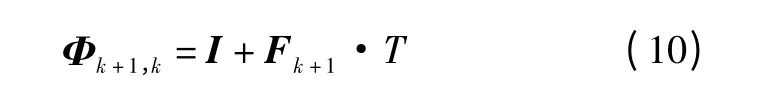
为系统状态转移矩阵，I 为6 ×6 阶单位矩阵;雅可比矩阵为

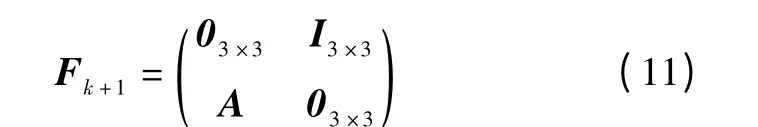
其中，03×3为3 ×3 阶零矩阵，I3×3为3 ×3 阶单位矩阵，

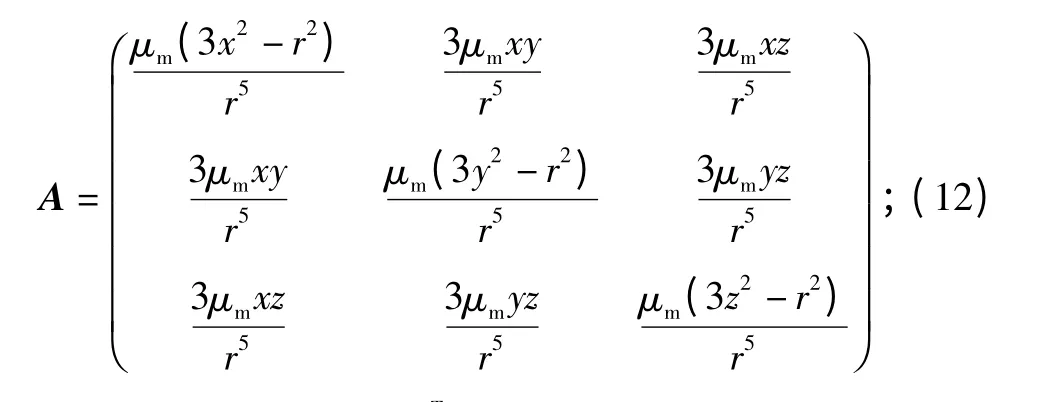
根据PWCS 可观测性分析方法，系统可观测性矩阵O 定义为

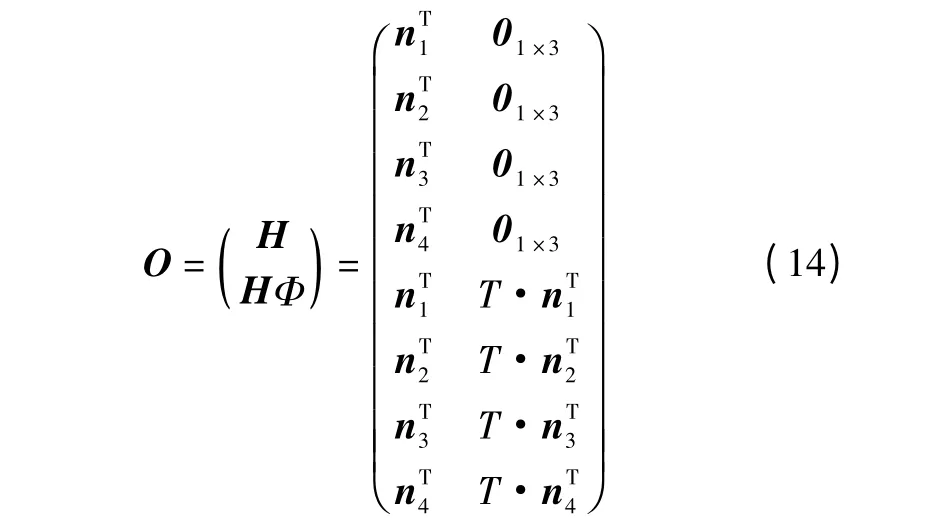
3 仿真结果与分析

月球卫星的标称轨迹由STK 生成，选取的4 颗脉冲星如表1 所示。仿真条件如下。

1)月球卫星轨道参数:半长轴为1938．2 km，偏心率为0°，倾角为0°，赤经为0°，近地点幅角为0°;

2)采样时间为500 s;

3)X 射线探测器面积为1 m2;

由于系统是非线性的，选择EKF 滤波算法来估计导航系统的状态。仿真结果如图3 ～图4 所示，状态估计误差均值如表3 所示。

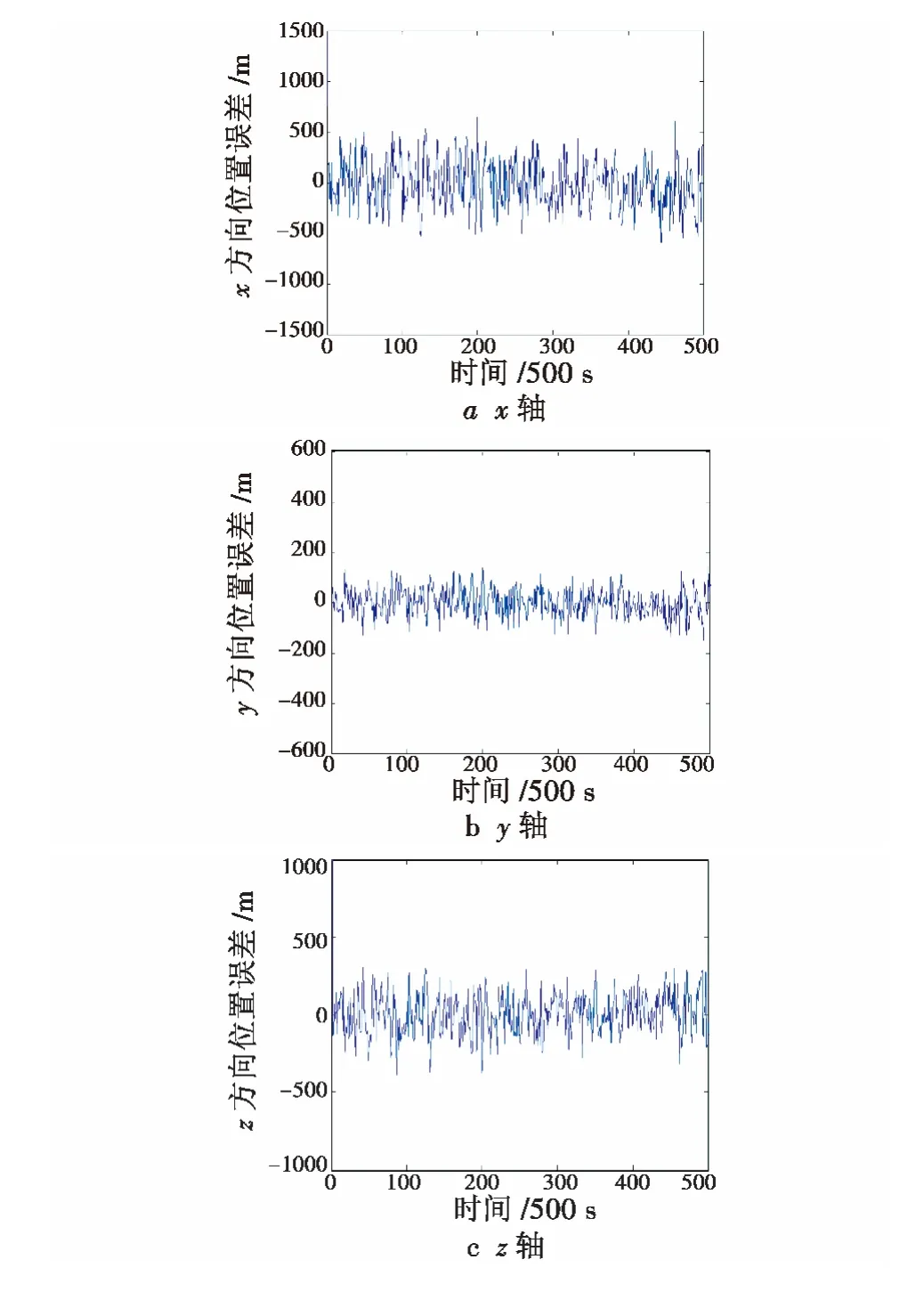
图3 各轴上的位置误差Fig．3 Position estimation error of each axis

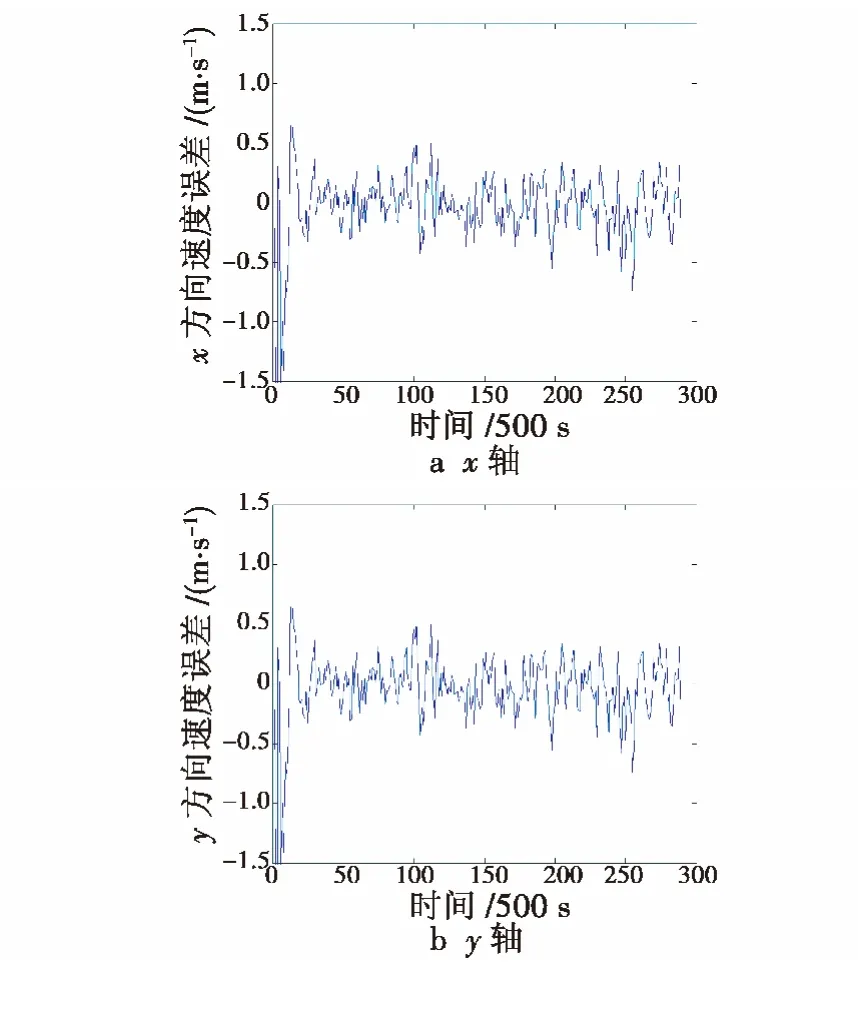
图4 各轴上的速度误差Fig．4 Velocity estimation error of each axis

表3 状态估计误差均值Table 3 The average values of estimation errors

图3 ～图4 和表3 分别给出了x，y 和z 轴上的位置和速度误差曲线及误差均值，该导航方法能够提供月球卫星位置和速度，并且达到较高的导航精度，是一种适于月球卫星自主导航的方法。

4 结束语

本文提出一种基于X 射线脉冲星的月球卫星自主导航方法，以月球卫星的位置和速度作为状态量，X射线探测器获得的脉冲到达时间作为观测量，分析了脉冲星的距离测量精度，并采用PWCS 可观测性分析方法对导航系统进行可观测性分析，结果表明系统是完全可观测的，最后采用卫星导航领域广泛使用的EKF 滤波算法进行状态估计，该导航系统能够提供较高精度的位置和速度信息。因此，该方法是一种可行的月球卫星自主导航方法。

［1］ 宁晓琳，马辛．基于天文和陆标观测的月球卫星自主导航方法［J］．宇航学报，2010，31(7):1737-1747．(NING X L，MA X． Autonomous navigation for lunar satellites using celestial objects and landmarks［J］．Journal of Astronautics，2010，31(7):1737-1747．)

［2］ 吴伟仁，王大轶，宁晓琳．深空探测器自主导航原理与技术［M］． 北京:中国宇航出版社，2011． (WU W R，WANG D Y，NING X L．Autonomous navigation principles and techniques for deep space probes［M］．Beijing:China Astronautic Publishing House，2011．)

［3］ NING X L，FANG J C． Spacecraft autonomous navigation using unscented particle filter-based celestial/Doppler information fusion［J］．Measurement Science ＆ Technology，2008，19(9)．doi:10．108810957-0233/19/9/095203．

［4］ 潘晓刚，矫媛媛，周海银．基于多传感器天文信息的自主主导航算法及可观测性分析［J］．空间科学学报，2014，34(1):116-126．(PAN X G，JIAO Y Y，ZHOU H Y．Algorithm of astronomy autonomous navigation based on multisensor and the analysis of observability［J］．Chinese Journal of Space Science，2014，34(1):116-126．)

［5］ SHEIKH S I，PINES D J，RAY P S，et al．Spacecraft navigation using X-ray pulsars［J］．Journal of Guidance Control and Dynamics，2006，29(1):49-63．

［6］ 杨成伟，郑建华，李明涛，等．晕轨道X 射线脉冲星自主导航和轨道维持研究［J］．武汉大学学报:信息科学版，2014，39(3):258-261．(YANG C W，ZHENG J H，LI M T，et al．Autonomous navigation and control in halo orbit based on XNAV［J］．Geomatics and Information Science of Wuhan University，2014，39(3):258-261．)

［7］ 费保俊，姚国政，杜健，等．X 射线脉冲星导航研究的若干问题［J］． 装甲兵工程学院学报，2013，27(3):1-8．(FEI B J，YAO G Z，DU J，et al．Some problems of research on X-ray pulsar-based navigation［J］．Journal of Academy of Armored Force Engineering，2013，27(3):1-8．)

［8］ 李茂登，荆武兴，黄翔宇．考虑月球扁率修正的月球卫星自主导航［J］． 宇航学报，2012，33(7):896-902． (LI M D，JING W X，HUANG X． Autonomous navigation for lunar satellite with lunar oblateness correction［J］．Journal of Astronautics，2012，33(7):896-902．)

［9］ LIU J，MA J，TIAN J W，et al．X-ray pulsar navigation method for spacecraft with pulsar direction error［J］．Advances in Space Research，2010，46(11):1409-1417．

［10］ WU J Y，YANG Z H，YANG N N．The accuracy analysis of the spacecraft autonomous navigation system based on X-ray pulsars［J］． Proceedings of the Institution of Mechanical Engineers，Part I:Journal of Systems and Control Engineering，2013，227(1):121-128．

［11］ SHEIKH S I，PINES D J．Recursive estimation of spacecraft position and velocity using X-ray pulsars time of arrival measurements［J］．Navigation，Journal of the Institute of Navigation，2006，53(3):149-166．

［12］ 帅平，陈定昌，江涌．GPS/SINS 组合导航系统状态的可观测度分析方法［J］．宇航学报，2004，25(2):219-224．(SHUAI P，CHEN D C，JIANG Y．Observable degree analysis method of integrated GPS/SINS navigation system［J］．Journal of Astronautics，2004，25(2):219-224．)

［13］ GOSHEN-MESKIN D，BAR-ITZHACK I Y．Observability analysis of piece-wise constant system-part I:theory［J］． IEEE Transactions on Aerospace and Electronics Systems，1992，28(4):1056-1067．