地空通信中基于贪婪算法的SC-FDE 系统稀疏信道估计

王 宁， 郭 英， 张东伟， 张坤峰， 李红光

(空军工程大学信息与导航学院，西安 710077)

0 引言

随着地空通信对高速数传的需求日益迫切，要求地空通信系统必须具备较高数据传输能力。近年来兴起的单载波频域均衡(Single-Carrier Frequency-Domain Equalization，SC-FDE)系统采用单载波系统的传输方式及多载波系统的信号处理方法，能够有效提高传输速率，同时可避免多载波峰平比(PAPR)高、对频偏敏感等缺陷［1］。文献［2 -3］介绍了SC-FDE 技术在地空传输系统中的应用，研究表明在高速传输过程中SCFDE 系统具有良好的信息传输可靠性。

在SC-FDE 系统中，信道估计的准确与否直接影响均衡性能。传统的SC-FDE 系统中采用基于最小二乘(Least-Squares，LS)准则的信道估计算法，该算法原理简单，但其在低信噪比传输环境中误差较大。近年来兴起的压缩感知理论开辟了一种全新的信号采集处理算法，广泛应用于信号处理的各项领域。文献［4］介绍了压缩感知技术在稀疏多径信道估计中的应用，研究结果显示其具有良好的估计性能;文献［5］介绍了基于压缩感知的MIMO-OFDM 水声通信信道估计算法;文献［6］介绍了水声单载波分块传输中基于压缩感知的稀疏信道估计算法，研究结果表明新的压缩感知信道估计算法较传统的LS 信道估计算法更加准确。

地空无线信道可视为由一个直射波成分和多个散射波成分组成的多径信道，即Rice 信道模型［7］，因此其信道冲激响应具有时域稀疏特性，本文提出了基于贪婪算法的SC-FDE 稀疏信道估计算法，研究结果表明利用该算法所得信道估计结果更加准确。

1 SC-FDE 地空通信系统

基本的SC-FDE 系统结构如图1 所示。

图1 单载波频域均衡系统结构框图Fig．1 Block diagram of SC-FDE system structure

对照图1，系统具体信号流程如下所述。

1)发送端信号流程。输入信号通过正交相移键控(Quadrature Phase Shift Keyin，QPSK)映射后进行串并转换，转换后并行的N 点长的数据块即为接收端进行频域均衡的数据块，之后插入长度为Ns的循环前缀以降低块间串扰，至此，构造出了N + Ns长的传输符号，再进行并串转换将信号转换为串行信号，插入导频信号后将其调制再送入信道。

2)接收端信号流程。接收端解调同步后分成两部分处理:其一是提取导频用于信道估计;其二是对每个传输符号去掉循环前缀后将其变换到频域，以信道估计获得的信道响应结果对该频域信号进行均衡，之后再恢复到时域进行解映射，判决后就得到了系统传输的信息。

3)数学描述。设信源输出每N 个映射后的码元x(n)组成一个传输符号，假设发送信号的平均功率为P，信道冲激响应为h(n)，接收端去掉循环前缀后得到的信号可以表示为

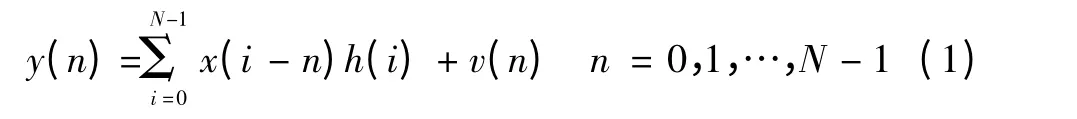
式中:x(i-n)为发送信号;h(i)为信号冲击响应;v(n)为加性高斯白噪声，且E{v(n)}=0，D{v(n)}=σ2，其中，E 为信号期望，D 为信号方差，σ2为噪声能量。经过快速傅里叶变换(FFT)变换到频域后，接收信号Yk可表示为

式中:Xk为发射信号;Hk为信道频域响应;Vk为噪声的频谱。频域均衡后得到接收信号Zk，则

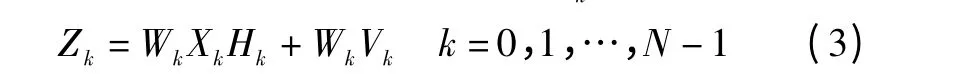
式中，Wk为频域均衡系数。采用最小均方误差准则(MMSE)进行均衡，即

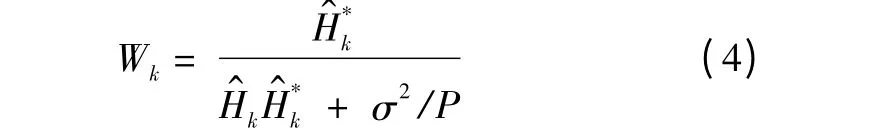
经过快速傅里叶逆变换(IFFT)后信号为

2 基于稀疏重构的信道估计方法

2．1 稀疏信道模型

信号经过地空信道衰落后的包络幅值一般服从莱斯分布，即信息经过地空衰落信道后，接收信号由直射路径信号与多个多径信号叠加而成，那么长度为N 的多径信道h=(h(0)h(1)… h(N -1))T的时域冲激响应可表示为

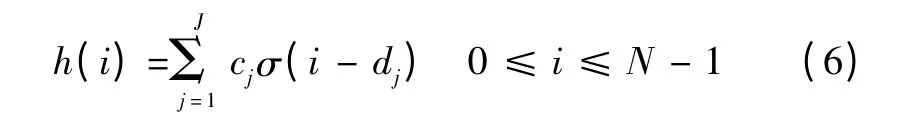
式中:J 为多径信道的路径个数;cj和dj分别为第j 条路径上的复增益和延时［8］;σ 为冲击函数。若J ＜＜N时，则信道呈明显的稀疏性。

2．2 信道估计

SC-FDE 系统中通常利用导频信号进行信道估计，导频一般采用具有时频域恒幅特性和良好自相关性的UW(Unique Word)序列，IEEE802．16 协议规定的UW 是Frank_Zadoff 序列和Chu 序列［9］。本文选取Chu 序列作为导频信号进行分析，设发送的导频信号为x =(x(0)x(1)… x(N-1))T，信道冲击响应为h =(h(0)h(1)… h(N-1))T，N 表示信道时域采样点数，由于信道具有稀疏特性，其中仅有J 个取值较大，其他各点取值趋近于零，且J ＜＜N，则式(1)用矩阵形式表示为

式中:v 为噪声向量;X 为N × N 的发射导频信号矩阵，即

若导频采用Chu 序列，则所发送的Chu 序列(训练序列)为

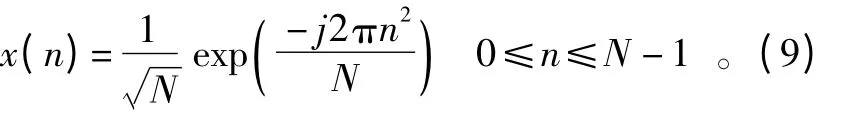
2．2．1 基于LS 准则信道估计方法

LS 信道估计方法是单载波频域均衡系统中最常用的一种信道估计方法。在式(7)中，根据LS 准则得到的信道估计值可表示为

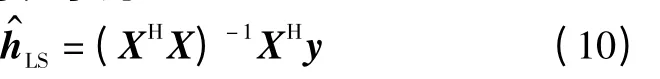
在不同信噪比下，定义SC-FDE 地空通信系统中信道估计归一化均方误差ENMSE为

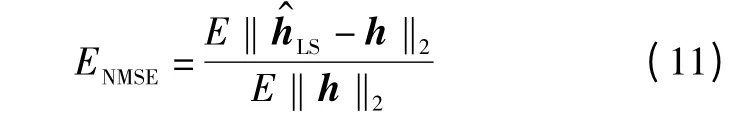
式中，E 为均值。将式(10)代入式(11)，则基于LS 准则的信道估计误差为

2．2．2 基于稀疏重构的信道估计方法

贪婪算法是一种典型的稀疏重构算法，该算法通过逐步选取对压缩测量值产生最大影响的列向量来实现对原始信号的最优估计。本文主要研究基于贪婪算法中典型的正交匹配追踪(OMP)算法及对其改进的压缩采样匹配追踪(CoSaMP)算法的信道估计方法。将上文中的X 作为测量矩阵，y = (y(0)y(1)…y(N-1))T作为观测向量，通过稀疏重构的方法在X中选取最少的列向量作为基向量，找到能够对观测向量y∈CM进行线性表示的系数向量h^∈CN(M≤N)，此为信道响应的估计值，即

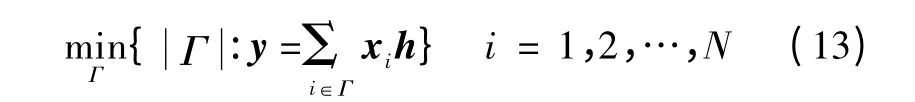
式中:Γ 为支撑集;xi为压缩测量矩阵的第i 列向量。

根据压缩感知理论，测量矩阵需满足RIP 条件，即对任意稀疏度为J 的稀疏信号s 和常数δJ∈(0，1)，测量矩阵X 需满足

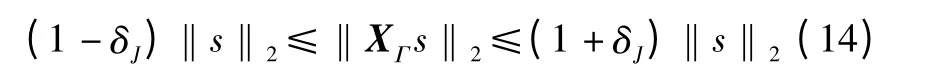
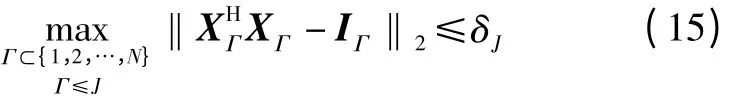
根据文献［10］，任意N×N 矩阵X∈RIP(J，δJ)等价于由上述可知XHΓXΓ=IΓ，显然有‖XHΓXΓ-IΓ‖2≡0，对于任意常数δJ，式(15)恒成立，因此X 满足RIP 条件。

1)OMP 算法。OMP 算法的思想是:将残差向量在字典上进行线性分解，残差初始值即为观测向量r0=y，字典即为测量矩阵X，X 中所有列向量具有归一化的模，重构允许误差为e。每次迭代都从字典的列向量中选取一个与残差相关系数最大的列向量，即残差在该列向量上的投影最大，可以表示为

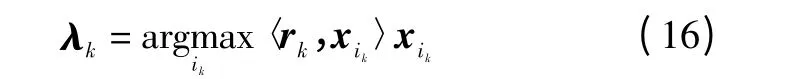
式中:〈，〉表示两个向量的内积;向量xik为X 中第i 个列向量，i=1，2，…，N。

对残差值做更新

计算信道估计值h^k，h^k满足最小优化问题

式(18)是一个二次函数最小化问题，求目标函数对h^k的微分，令导数为零即可得到，即

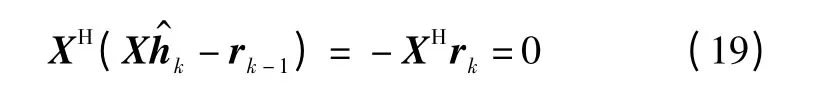
为使式(19)成立，需要令X 中列向量与残差rk正交，此即正交匹配的概念。停止迭代的条件为‖rk‖22 ＜e，或者迭代次数大于压缩采样序列的长度，否则重复执行上述步骤。

2)CoSaMP 算法。对于2．2 节中地空信道的系统模型，若感知矩阵X 满足约束等距条件，对于k 稀疏的信道h，则在Euclidean 范数空间上，观测向量u =X*Xh的任意S 项对应于h 的S 个项，则可将向量u 看作h 的代替。CoSaMP 算法首先选择观测向量中最大的2S 个项，并将这些项的索引位置集合并到已有的支撑集中，然后通过最小二乘准则来得到估计值a。

基于CoSaMP 算法的信道估计方法实现流程为输入测量矩阵X，观测向量r0=y，信号稀疏度s，允许误差ε。具体流程如图2 所示。

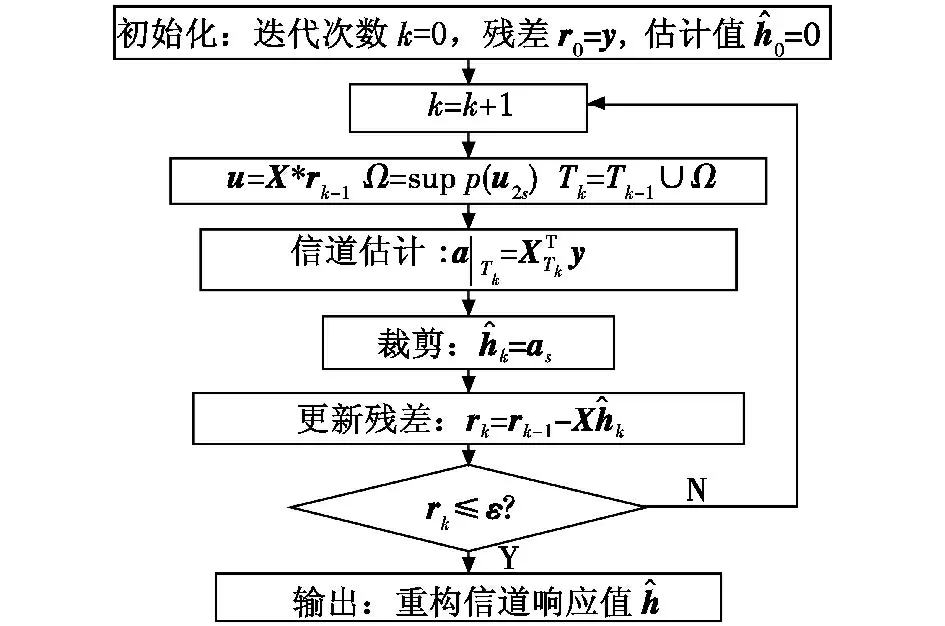
图2 CoSaMP 算法流程图Fig．2 Flow chart of CoSaMP

3 仿真与分析

实验1 各重构算法重构概率。

分别采用OMP 算法和CoSaMP 算法对长度M =100 的信号进行重构，当稀疏度k 分别为5 和10 的时候，考察信号采用不同长度的压缩采样值进行信号重构的重构概率。实验中信号幅度为1，所加高斯白噪声方差σ2为0．1，重构允许误差为1 ×10-5，每个压缩采样序列长度下进行200 次实验，并将重构概率平均。仿真结果如图3 所示，实验表明，在相同的压缩采样序列长度下CoSaMP 算法比OMP 算法具有更好的重构性能，且整体来看，CoSaMP 算法具有更好的稳定性和鲁棒性。

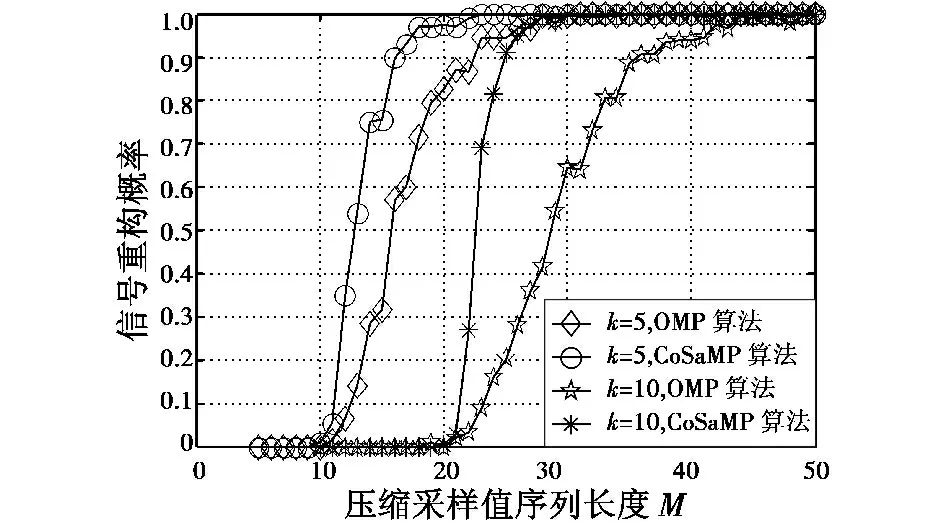
图3 信号重构概率与采样序列长度关系Fig．3 Relationship of signal reconstruction probability and sampling sequence length

实验2 不同算法下的信道估计对比。

信道时域采样点数为96，路径为4 条，功率衰减分别为0 dB，5 dB，10 dB，15 dB，各径延时分别为0 μs，1．25 μs，2．5 μs，3．75 μs，不受噪声影响的多径信道冲击响应如图4a 所示。压缩采样序列长度为96，图4b、图4c、图4d 分别为OMP，CoSaMP，LS 算法下信噪比为0 dB 时所估计得到的信道冲击响应。实验结果表明CoSaMP 算法估计性能最好，其次为OMP 算法，而LS信道估计算法性能最差。

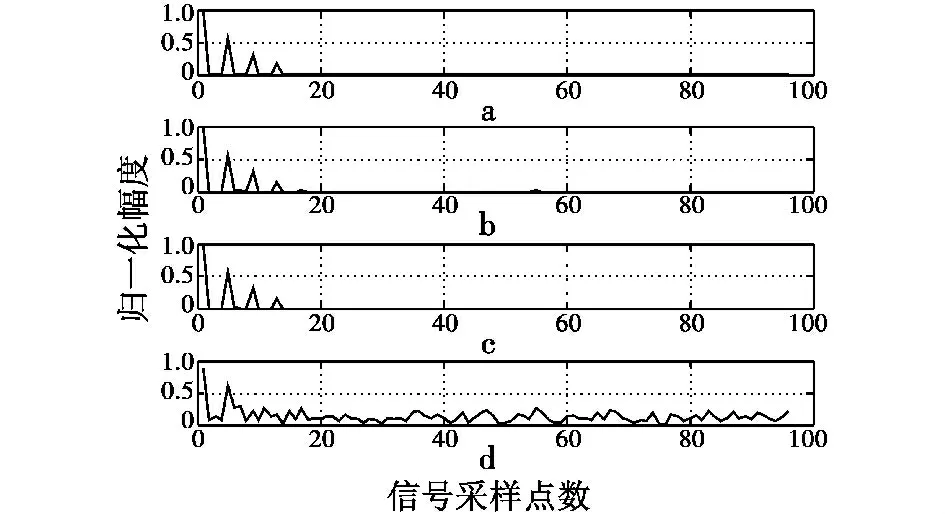
图4 不同估计算法得到的信道冲击响应Fig．4 Channel impulse response of different estimation algorithms

图5 所示为各算法下的信道估计NMSE。实验表明，在低信噪比条件下，基于稀疏重构的信道估计算法相比于LS 算法性能有明显提升，在高信噪比条件下，各算法性能相近。

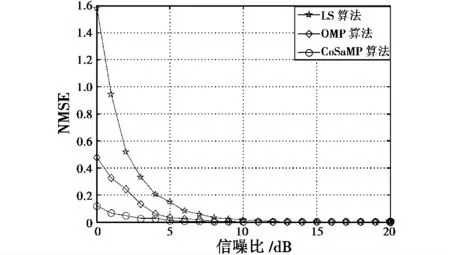
图5 信道估计归一化均方误差Fig．5 Normalized mean square error of channel estimation

实验3 系统误码率统计。

基于IEEE802．16 推荐的帧格式，导频由两个长度为96 的UW(本文采用Chu 序列)组成，每帧包含10个数据块，每个数据块包含224 个信息码元和一个长32 的UW 序列，其作用与循环前缀相同，目的是降低符号间串扰，FFT 运算点数为256。

系统帧结构如图6 所示。

图6 系统帧结构Fig．6 The structure of system frame

码元速率为8 MHz，采样频率为32 MHz，相移为π/4，调制方式为QPSK 调制。

信道模型为:1 条主径，3 条延迟径，噪声为加性高斯白噪声，各径时延及功率衰减见表1。

图7 为在MMSE 均衡准则下，基于各信道估计算法的系统误码率随信噪比变化曲线图。由图可看出，采用CoSaMP 算法进行信道估计所得的系统误码性能最好，相比于传统的LS 算法有3 dB 左右的性能提升，OMP 算法次之，相比于LS 算法有2 dB 左右的性能提升。

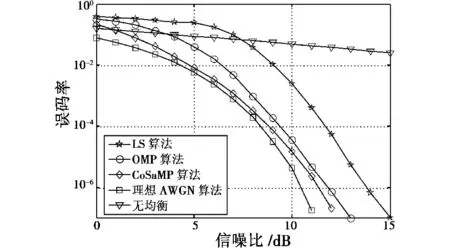
图7 不同算法误码率Fig．7 BER performance of different algorithms

表1 多径分布Table 1 Multipath distribution

4 结论

针对地空信道的时域稀疏特性，本文在SC-FDE系统中提出了基于贪婪算法的信道估计算法，分析证明了基于Chu 序列的导频矩阵满足RIP 条件，以其作为测量矩阵，将地空信道估计问题构造为稀疏重构模型，采用贪婪算法中的OMP 算法和CoSaMP 算法进行信道估计，仿真验证了基于稀疏重构的信道估计算法与传统的LS 算法相比，信道估计更加准确，系统误码性能有明显改善。

［1］ 陈强，杨霄鹏，欧阳超，等．基于TD-NLMS 的航空移动通信OFDM 系统载波频率偏移消除［J］．空军工程大学学报:自然科学版，2013，14(1):71-74．(CHEN Q，YANG X P，OUYANG C，et al．Elimination of carrier frequency offset in aeronautical mobile communication OFDM system based on TD-NLMS algorithm［J］．Journal of Air Force Engineering University:Natural Science Edition，2013，14(1):71-74．)

［2］ 王宁，郭英，张坤峰，等． 地空数据传输系统中单载波频域预均衡技术研究［J］．空军工程大学学报:自然科学版，2014，15(5):66-70． (WANG N，GUO Y，ZHANG K F，et al． Single carrier frequency domain pre-equalization applied to ground-to-air data transmission system［J］．Journal of Air Force Engineering University:Natural Science Edition，2014，15(5):66-70．)

［3］ YU X L，SONG D D，YANG Z X．Aeronautical channel modeling in frequency-domain for block-data transmission systems［C］//IEEE International Conference on Computer Science and Automation Engineering (CSAE)，2011:719-723．

［4］ BERGER C R，WANG Z H，HUANG J Z，et al．Application of compressive sensing to sparse channel estimation［J］． IEEE Communications Magazine，2010，48(11):164-172．

［5］ 王妮娜，桂冠，苏泳涛，等．基于压缩感知的MIMO-OFDM系统稀疏信道估计方法［J］．电子科技大学学报，2013，42(1):58-62．(WANG N N，GUI G，SU Y T，et al．Compressive sensing-based sparse channel estimation method for MIMO-OFDM systems［J］． Journal of University of Electronic Science and Technology of China，2013，42(1):58-62．)

［6］ 孟庆微，黄建国，韩晶，等． 水声单载波分块传输中基于压缩感知的稀疏信道估计方法［J］． 北京邮电大学学报，2012，35(5):14-17． (MENG Q W，HUANG J G，HAN J，et al． Compressed sensing based sparse channel estimation method for underwater single carrier block transmission［J］． Journal of Beijing University of Posts and Telecommunications，2012，35(5):14-17．)

［7］ HAAS E．Aeronautical channel modeling［J］． IEEE Transactions on Vehicular Technology，2002，51(2):254-264．

［8］ YU X L，SONG D D，YANG Z X．Aeronautical channel modeling in frequency-domain for block-data transmission systems［C］//IEEE International Conference on Computer Science and Automation Engineering(CSAE)，2011，4:719-723．

［9］ IEEE Std 802．16-2004．Air interface for fixed broadband wireless access systems［S］．New York:LAN/MAN Standards Committee，2004．

［10］ RUDELSON M，VERSHYNIN R． On sparse reconstruction from Fourier and Gaussian measurements［J］．Communications on Applied Mathematics，2008，61 (8):1025-1045．