剖析思路知立意,品悟精神识导向
——2015年淮安中考卷第28题的思考
☉江苏省金湖县吕良中心初级中学 乔太华
剖析思路知立意,品悟精神识导向
——2015年淮安中考卷第28题的思考
☉江苏省金湖县吕良中心初级中学 乔太华
随着2015年全国各地中考大幕徐徐落下,一份份凝聚了命题组教师心血的试卷大放异彩,中考压轴题作为一份试卷的核心,具有知识容量丰富、解题方法多样、能力要求较高、思想方法运用活等特点,其承载的教学价值令人回味无穷,导向深远.现以2015年淮安中考卷第28题为例,谈谈笔者的一些认识.
题目(江苏淮安中考第28题)如图1,在Rt△ABC中,∠ACB= 90°,AC=6,BC=8.动点M从点A出发,以每秒1个单位长度的速度沿AB向点B匀速运动;同时,动点N从点B出发,以每秒3个单位长度的速度沿BA向点A匀速运动.过线段MN的中点G作边AB的垂线,垂足为点G,交△ABC的另一边于点P,连接PM、PN.当点N运动到点A时,M、N两点同时停止运动,设运动时间为t秒.
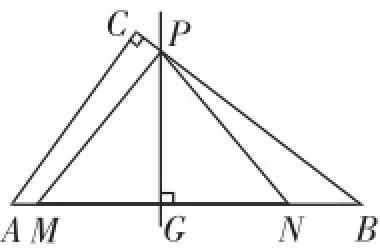
图1
(1)当t=_______秒时,动点M、N相遇.
(2)设△PMN的面积为S,求S与t之间的函数关系式.
(3)取线段PM的中点K,连接KA、KC.在整个运动过程中,△KAC的面积是否变化?若变化,直接写出它的最大值和最小值;若不变化,请说明理由.
一、探索思路
第一问属于“同时出发相向而行到第一次相遇问题”,通过列一元一次方程或直接利用算术方法即可求出t=2.5,属于送分题.但是此问可以引导考生对M、N两点的运动情形进行初步分析,同时因为简单可以缓解考生的焦虑情绪.
第二问是求动态情形下图形的面积问题,图中△PMN由边MN和高PG确定,所以解题思路是:首先,对M、N两点的运动情形进行分析,确定边MN的变化,对边MN进行分类;第二步,根据边MN的每一种情形,再对高PG进行分类,确定总的分类情形;第三步,针对每一种情形画出图形,观察△PMN的位置和形状,最后确定求△PMN的面积的方法.
分类的难点是高PG,为了准确对高PG进行分类,对M、N两点位置的精确性要求比较高,所以画图不能太随意.通过对条件分析和画图观察可确定高PG的运动规律,从起始位置开始画图,让点M、N运动,观察中点G是如何运动的.相遇前,因为“动点N的速度是动点M的速度的3倍”,所以NG缩短快,而MG缩短慢,所以点G一直向点A运动,又相遇点在AB边上的高的左边,因此相遇前高PG的位置有2种,即点P先在CB上,再到CA上.相遇后,GN增加快,GM增加慢,所以点G也一直向点A运动,因此到结束点P就一直在AC上,所以本问可分3种情形.

图2

图3

图4
接下来,先分析计算确定分界点的时间,即要求出高PG与△ABC的高CH重合的时间,M、N两点相遇的时间,动点N到终点的时间,以及点M的位置,分类计算即可.
对于每种情形,先用含t的代数式表示出MN的长,然后利用相似三角形的性质或三角形函数求出高PG即可.结果如下所示.
①当0<t≤1.4时(如图2),MN=10-4t,PG=(t+5).

第三问是求动态情形下图形面积的最值问题,这里提供三种思路.
思路1:(特殊猜想法)中考压轴题的问题设计,往往都是层层递进的命题方式.因为点K是线段PM的中点,所以可以考虑把第二问中的起点、两个分界点、终点计算出来,取其中的最大值和最小值.
上面的思路1并不能确定结果的正确性,但是时间不够或没有其他方法的同学不妨一试.思路2可以使结果的正确性大大提高.
思路2:(操作观察法)首先利用圆规截取的方法,确定几个点M、N的位置,然后观察点K的运动轨迹,可以发现,点K一直在边AB的某一条固定的垂线上做折返型运动,由于△KAC的边AC确定,所以只需探索点K到AB的距离的变化规律即可,结果如下所示.
当点P与点C重合,即t=1.4s上时(如图6),△KAC的面积最小,此时△KAC的面积为1.68.
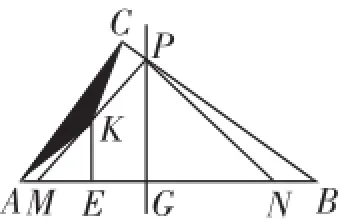
图5

图6
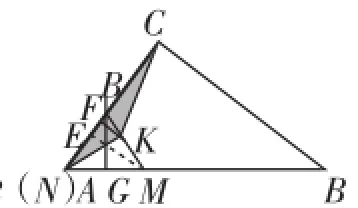
图7
思路3:(代数法)根据第三问的三种情形,分别求出K到AC的距离,列出△KAC的面积与t的函数关系式,根据函数关系式和t的取值范围来确定△KAC的面积的最大值和最小值.
数学学习本身就是一个过程,如何在考试中考查“看不见、摸不到”的活动过程呢?从上述思路探析中不难看出,本题各问层级分明,逐级递进,引导学生不断思考,变考试过程为学习、研究的过程.学生在解决这一系列问题的过程中,可以表现自己的观察、猜想、比较、构造及证明等数学活动方面的能力,有效考查学生的数学素养,在一定程度上体现了对过程性目标的考查.从而促使教师在平时的数学教学中重视过程的教学,使学生经历知识的发生、发展及运用过程,并启发学生及时进行归纳、总结和反思,积累解决问题的策略及经验,不断提升数学能力.
二、品悟精神
近几年来,淮安市中考压轴题都以图形运动中探求图形面积或判断图形形状为背景进行命题.今年的图形更加简单,运动过程也不复杂,但是考查的各项指标和需求并没有减少.
1.摈弃繁难堆砌,重视数学能力
本题涉及的知识点不多,没有将大量的数学知识进行堆砌,重点考查学生的数学能力.在分析图形运动时,对于底MN和高PG的分类,需要较强的动手操作能力和空间想象能力,捕捉图形信息及对信息处理和转化的能力.对于△KAC的面积的最大值和最小值的确定,需要几何直观能力、动手操作能力和合情推理能力.归纳概括得到猜想和规律,并加以验证,是创新的重要方法,对底MN和高PG的分类及对△KAC的面积的最大值和最小值的探求充分体现了这些方法.在具体三角形的面积计算中,需要从复杂图形中分解基本图形和作辅助线构造基本图形,需要较强的化归迁移能力和利用模型解决问题的能力.
2.突出数学思想,注重数学思考
哈佛校长M.劳厄尔曾说“教育,是指所有学会的东西都忘却了以后仍然留下来的那些东西.”本题并非解题方法和技巧的机械运用,而是巧妙考查分类讨论思想、模型思想、化归思想等,从培养学生的数学素养及综合能力的层面上关注学生的数学理性思维,展现了数学的学科价值和人文价值.
分类思想:求△PMN的面积时,需要对底MN和高PG的位置进行分类,求△KAC的面积时,需要对K的位置进行分类.
模型思想和化归思想:通过对相似三角形的基本图形的提取和作辅助线构造基本图形,体现了模型思想和化归思想的应用.
3.关注学习过程,体现数学观念
对于运动型问题,首先由于运动产生变化,会出现众多的情形,所以要进行分类,然后一类一类地解决问题;对于第三问,可以通过操作,然后观察、猜想、验证一系列的活动进行求解.“用适当的方法产生若干个研究对象,用抽象、概括的方法确定研究对象的本质特征后下定义,用特殊到一般合情推理的方法猜想规律,用演绎推理的方法证明结论”,这些都是思考问题的一般方法、套路,体现了数学观念.
三、启示教学
鉴于上述思考,在平时教学中,我们要加强以下三个方面的教学.
1.养成认真审题的习惯
从阅卷和考试后的调查发现,好多学生对高PG的位置变化弄不清楚,一部分学生认为高PG就在CB上,原因是根本没有明白“动点N的速度是动点M的速度的3倍”这个隐含条件,从他们画的图上面即可看出,另一部分学生认为高PG的位置应该分三种情形,点P先在CB上,再到CA上,最后又回到CB上,虽然他们对“动点N的速度是动点M的速度的3倍”这个隐含条件有关注,但是对点M的最终位置思考太随便,画出的图形误差太大,从而出现点P最后又回到CB上的情形,还有一部分学生根本没有注意动点的终点,从而出现了错误.
“授人以鱼不如授人以渔.”平时教学,我们不能代替学生读题、审题,要教给学生快速捕捉有用信息的方法,如在阅读过程中采用“划去无关语句”的方法提取关键语句,或画出关键语句,在图形上标出已知数据和未知数据,把相关的量用含变量的式子表示出来等.
2.提升动手操作的能力
对于本题,从阅卷和考试后的调查发现,许多学生没有能通过画图发现高PG的位置变化情形和点K的运动轨迹,原因是无法精确画出BN=3AM,其实,直接在原图上,用圆规以适当的长度从A、B两端分别截取一些相等的线段即可.
我们在平时的教学中,一定要加强学生动手操作的教学指导,不能因为麻烦而随意将动手操作活动舍弃.首先要加强尺规作图和画图的教学,在掌握一些基本的作图方法的基础上,要让学生深刻掌握画图工具(圆规、直尺、三角板、量角器等)的基本功能,如圆规的截取、画弧等功能,同时还要能根据问题情景选择匹配的画图工具,如遇到旋转问题,想到用圆规;其次,要培养学生就地取材、合理利用现有的材料进行操作的能力,如利用长方形稿纸、长方体状的橡皮、圆柱体状的铅笔进行即时操作.
“纸上得来总觉浅,绝知此事要躬行.”“动手操作”不仅是为了考试,“动手操作”是一种重要的学习方式,“动手操作”犹如数学课堂的“强心剂”,一方面帮助学生理解知识,增强学生的学习兴趣和自信心,另一方面对教师来说,在教学中很容易达到事半功倍的效果.数学教学中,教师要向学生提供充分的操作活动机会,让学生在动手操作中体验到数学的乐趣,并引导学生在动手操作中加深对知识的感悟,在动手操作中提高解决问题的能力,发展创造性思维.
3.夯实基础,重视通法、通则
对于本题,许多学生在第二问和第三问得零分,其实第二问学生认真算出一种情况应该还是可以的,第三问找几个特殊位置算一算也能“蒙”到不少分数,可是就是不会算,几种情形都画对的同学中有许多都在计算上功亏一篑.
绝大部分中考试题源于教材,是教材中题目的引申、变化或组合.中考题的形式和知识背景千变万化,但是其中蕴含的数学思想方法往往是相通的.因此,在日常教学和复习中强调通性通法,同时要处理好通法和技巧的关系,在学习中不应刻意追求特殊方法、技巧,因为这些东西只有在特定的条件下才能应用.考虑到教材的编排遵循“螺旋上升”的原则,知识点比较分散,所以在首轮复习中,我们必须“串读”教材,把相关内容进行分类、归纳、整理,形成完善的知识链.对成绩好的学生,应引导他们进行单元内知识点的整合,同时寻求各单元的交叉点、中间地带,把握它们的异同点.对于学习困难的学生,应指导完成教材中的题目,并要求他们注意解题方法的归纳和整理.
1.中华人民共和国教育部制定.义务教育数学课程标准(2011年版)[M].北京:北京师范大学出版社,2012.
2.乔太华,李东.立足师生发展,尽显一题之用——一道“探索研究”问题的教学实录及评析[J].中学数学(下),2014(9).
3.罗增儒.数学解题学引论[M].西安:陕西师范大学出版社,2008.
4.[美]波利亚.数学与猜想[M].北京:科技出版社,2011.
5.王红兵,卜以楼.从基本联想到优化思维——解析2015年南京市一道分类讨论中考题[J].中学数学(下),2015(9).Z

