基于多元表征理论的习题课教学实践——以“乘法公式”习题课为例

☉江苏省无锡市东林中学 杨峰☉江苏省无锡市金星中学 朱宸材

基于多元表征理论的习题课教学实践
——以“乘法公式”习题课为例

☉江苏省无锡市东林中学 杨峰☉江苏省无锡市金星中学 朱宸材

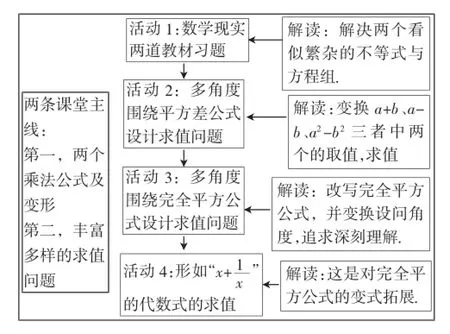
围绕乘法公式的教学研讨新授课居多，公开课、教研课中鲜见有相关习题课．然而乘法公式的习题丰富多样，仅从各级涉及乘法公式的考试来看，作为简化运算的价值只占了较少的份额，而有较多的试题都是乘法公式变形相关的求值题，但不少学生缺少这方面的变形适应性，常常容易丢分．为此，笔者最近基于“多元表征理论”开发了一节乘法公式的习题课，本文给出该课的教学设计和教学流程，供研讨．

一、乘法公式习题课教学设计

（一）教材习题，运用公式

活动1：解两道教材习题

教材习题1：解不等式（2x-5）2+（3x+1）2＞13（x2-10）.

讲评预设：直接出示教材上的习题，让学生独立思考，由获得思路的学生汇报求解方法，并追问不等式、方程的类型以前有没有见过，如果没有见过，为什么可以求解？它们的本质是什么类型的不等式或方程组呢？学生应该能答出来，经过化简、整理得到的是一元一次不等式、二元一次方程组．从而拓展学生对乘法公式的认识，乘法公式不仅可以简化运算，在一些繁杂的不等式、方程化简变形上也可起到重要的作用．接下来在黑板上书写乘法公式，为后续习题研究作准备．

（二）多角度利用平方差公式，设计求值问题

活动2：对平方差公式：（a+b）（a-b）=a2-b2变换赋值条件，设计求值练习

比如：先在黑板上取一些简单的数值，学生可以口算出来，接着，把上述赋值求值问题，改成数学练习题，如下所示.

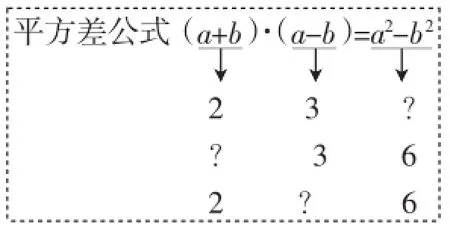
（1）已知a+b=2，a-b=3，求a2-b2的值；

（2）已知a2-b2=6，a-b=3，求a+b的值；

（3）已知a+b=2，a2-b2=6，求a-b的值．

还可以将上述改写为以方程组呈现的习题，如下所示.

预设意图：让学生看到这类求值题的本质，借助于平方差公式整体求解，特别是（4）～（6），不能看到方程组就想去解方程组，而应该先看清问题中的代数式的特点，再灵活选择解题途径．在这组问题讲评之后，安排两道训练题，检测一下学生理解的情况．

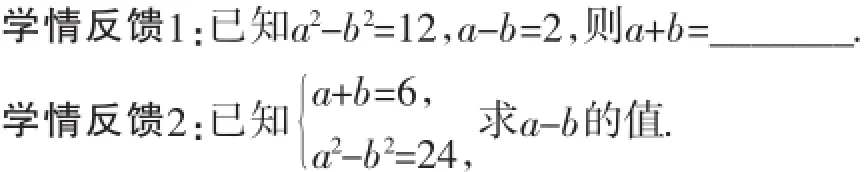
（三）多角度利用完全平方公式，设计求值问题

活动3：对完全平方公式：（a+b）2=a2+2ab+b2变换赋值条件，设计求值练习

依照前面平方差公式的赋值求值问题，也将完全平方公式改写，赋值，让学生口算，在黑板上形成如下板书.

接着安排学生把上述赋值问题重新设计成一些题目，预设如下.

（1）已知a2+b2=10，ab=3，求a+b的值；

（2）已知a+b=4，a2+b2=10，求ab的值；

（3）已知a+b=4，ab=3，求a2+b2的值．

在这组习题由学生编制出来之后，可以安排学生再练习一道类似的习题，体现学生自己的思考．接着再安排变式思考．

（4）已知（a+b-4）2+|ab-3|=0，求a2+b2的值．

（5）已知a-b=4，ab=3，求a2+b2的值．

变式意图：（4）是在（3）的基础之上增加一个解题层次；（5）由完全平方公式的一种形式（a+b）2=a2+2ab+b2过渡到另一种形式：（a-b）2=a2-2ab+b2.

预设意图：学生先独立思考，如果没有进展，则进行提示引导，让他们反复看“活动3”中的求解经验．如果学生发现少了条件，那么这个条件在这道问题中是否可以获得？通过一系列的启发引导学生发现思路，即本题中的

变式意图：通过系列变式改编，使学生对这类互为倒数式子和的变形达到较为深刻的理解，并善于从正、反两方向进行灵活变形求解．特别是对于（2），学生可能会漏解，要注意引导学生参与纠错与究错．

（五）课堂小结，检测反馈

问题：通过本课习题的学习，你对乘法公式有了哪些新的认识？

检测题：已知（m+n）2=25，（m-n）2=9．

（1）求mn的值；

（2）求m2+n2的值；

（3）求m2-n2的值；

（4）请再设计一道求值题．

附：教学流程图

二、教学立意的进一步阐释

1.预设习题起点，多元表征习题设问方式

从上面的活动设计来看，我们在进入题组训练之前都预设了一个相对简单易做的数学问题，如已知两数，求两数之积，将其与平方差公式结合起来，并与后续题组对应，而它们的本质却是一样的．这里可以提及所谓的“多元表征理论”，即人们关于数学概念（或数学问题）的心理表征往往包含多个不同的方面或成分，而且这些成分对于概念的正确理解都具有重要的作用，我们应高度重视这些成分之间的联系．基于此，“活动2”中，我们在呈现了（1）～（3）后，又从另外的角度给出（4）～（6），它们是“一一对应”的，目的是促进学生对这类问题结构的深刻认识和理解．

2.重视题组训练，追求“做一题，会一类，通一片”

根据解题教学经验，一题一讲，零散处理的方式远不及把同类问题集中在一起成为题组训练的效果来得好，如“活动3”中，尽管题组之下也只是几个小问，然而这几个小问从不同角度训练了完全平方公式的求值问题，要比在作业讲评时碰到一个讲一次，碰到第二种类型讲第二次效果要好．这样安排的目的是基于变式教学理论，让学生在变式中抓住问题的本质、洞察问题的结构，追求“做一题，会一类，通一片”．

1.王小林．优选精练重变式，示拙让学促生成——中考复习课中例习题教学设计的思考［J］．中学数学（下），2015（8）.

2.郑毓信.教师专业成长的主要目标与重要内容（下）［J］．小学教学（数学版），2013（12）.

3.刘东升．关联性：一个值得重视的研究领域［J］．中学数学（下），2013（12）.

4.季卫东．变式取向：从“标准模式”到“非标准模式”——以“轴对称最值问题”解题教学为例［J］．中学数学（下），2014（3）.Z