对一道五校联考题的研究

●王安寓(六合区实验高级中学江苏南京211500)

对一道五校联考题的研究

●王安寓(六合区实验高级中学江苏南京211500)

“直线与圆”是解析几何的重要组成部分，其地位同于圆锥曲线.各种考试都会命制质量上乘的考查直线与圆的位置关系的题目.求解该类题目，最关键的是灵活转化——将题目所给的条件灵活转化为相关的式子，要能透过表象看透本质，看透命题目的.

1 试题分析

例1已知△ABC的3个顶点为A(－1，0)，B(1，0)，C(3，2)，其外接圆为圆H.

1)求圆H的方程;

2)若直线l过点C，且被圆H截得的弦长为2，求直线l的方程;

3)对于线段HB上的任意一点P，若在以C为圆心的圆上都存在不同的2个点M，N，使得点M是线段PN的中点，求圆C的半径r的取值范围.

(2014年江苏省南通市五校联考第18题)

前2个小题的答案为:1)x2+(y－3)2=10; 2)x=3或4x－3y－6=0.本文主要研究第3)小题.

分析1由第1)小题知H(0，3).解析几何的一个特点是数形结合.首先作出符合题意的图形(如图1所示)，我们发现:此题中圆心虽定，但半径不定——圆C在动;点P带动点M，N运动，而且点M，N的位置对于点P还可能有第2种情况.4个动的元素间还没有一个定其余随之定的关系，而是既相互干扰又有变动.初读此题，觉得无从入手，找不到切入口.重新读题后，想到MN是圆的弦，而圆中既变(位置)又不变(长度)的弦是直径，是否可以从圆的直径入手?点P是线段HB上的动点，是否优先考虑HB的端点?联结HC，BC，易知HC＞BC，取CH的靠近点C的三等分点M0，以C为圆心、以为半径作圆，延长HC，与圆C交于点N0，则HM0=M0N0，符合题意(如图2所示).当点P是线段HB上任意一点时(不与点H重合)，联结PC并延长，与圆C交于点M1，N1，则

可将PM1N1绕点P旋转，则PM1变长，M1N1变短，到某一位置PMN时，必有PM=MN，即该圆C适合条件.随着圆C的半径增大，总可以用旋转的方法找到符合题意的割线PMN;而当圆C的半径太大时，直线HB与圆C不相离，不存在符合题意的割线;当圆C的半径太小时，联结HC，与圆C交于点M2，N2，则HM2＞M2N2，而M2N2是圆C中最长的弦，无论怎样旋转都不会有HM2=M2N2，不合题意.因此，求得圆C半径的范围是

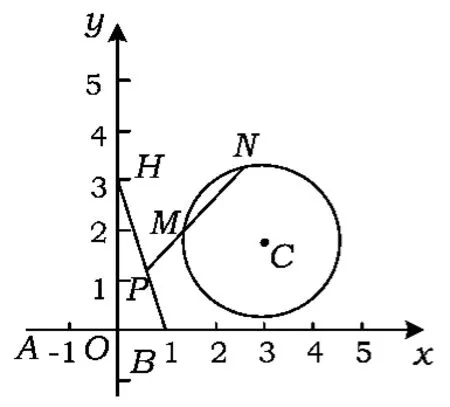
图1

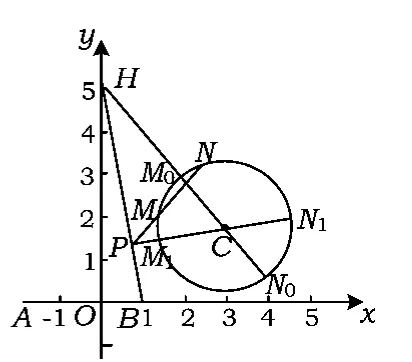
图2

分析2对任意点P∈HB，都有点P在圆C外，得CP－r＞0，但PM=MN如何转化?注意到MN是圆C的弦，因此联系圆C的直径，必有MN≤2r，PM是线段HB上任意一点与圆C上一点连线的长度，自然与圆心C有关.依据三角形中两边之差小于第三边得CP－r≤PM，从而形成不等式链0＜CP－r≤PM=MN≤2r，再考虑任意点P∈HB，自然转化为最值求解.

依题意得0＜CP－r≤PM=MN≤2r，即r＜CP≤3r恒成立，从而

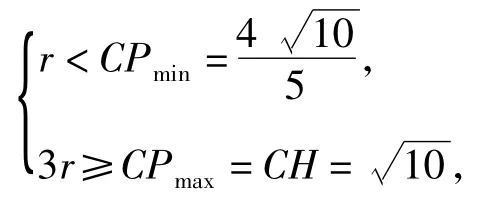
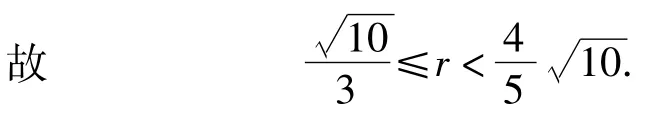
分析3从代数的角度思考，先求出BH的方程，设出点P，N的坐标，应用中点公式求得点M的坐标，进而考虑点M，N在圆C上，转化为2个圆有公共点的问题，再转化为函数的最值求解.

易求直线BH的方程为3x+y－3=0.设P(m，n)(其中0≤m≤1)，N(x，y).因为点M是线段PN的中点，所以

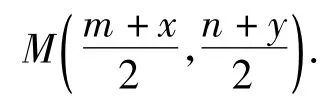
又因为点M，N都在半径为r的圆C上，所以

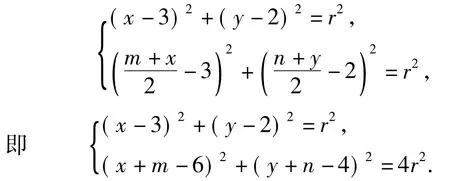
由该方程组有解，知2个圆(圆心为(3，2)、半径为r的圆和圆心为(6－m，4－n)、半径为2r的圆)有公共点，从而

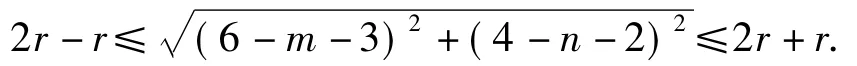
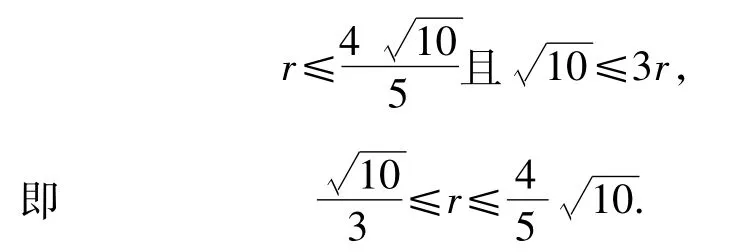
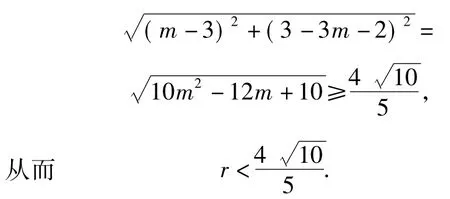
点评分析1是依托运动(旋转)找到解决问题的方法.而分析2是由点P在圆C外得PC－r＞0，由“三角形两边之差小于第三边”和“圆的弦中直径最长”，得到PC－r≤PM，MN≤2r，再由条件M为NP的中点，形成一个不等式链，通过恒成立达到解题的目的.对任意点P∈HB，都有r＜CP≤3r成立，运用函数思想，转化为最值求解.求解的过程简单，而思维的过程艰难.分析1呈现复杂而学生易于理解;分析2呈现简单而学生不易想到.如果把分析1的求解过程缩减，用相关的数学式子表征，那么就得到分析2.分析1是分析2的动态演示.分析3从代数的角度入手，将点点、点圆的位置关系通过式子表示出来，进而转化为函数的最值求解.分析3是分析2的代数化.

变式1已知点B(1，0)，H(0，3)，C(3，2)，P为线段HB上任意一点，过点P作以C为圆心的圆的割线PMN，与圆C交于点M，N.设M为PN的中点，则由所有满足上述条件的圆C组成的图形的面积为________.

分析由例1第3)小题的分析过程知，所有满足条件的圆组成的是一个圆环，其内径为，外径为，故其面积为

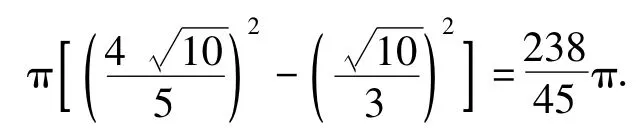
变式2已知点B(1，0)，H(0，3)，C(t，2)，P为线段HB上任意一点，过点P作以C为圆心、以为半径的圆的割线PMN，与圆C交于点M，N.设M为PN的中点，则实数t 的取值范围是______.

分析易求HB的垂直平分线方程为，与y=2交于点D(2，2).如图3，当圆心C位于点D的右侧时，HC＞BC，由例1第3)小题的分析过程知F(3，2)是点C的最右边的位置，易知点D到HB的距离为，从而当圆心C在线段DF上时，圆C符合题意;在直线y=2上在HB右侧的到HB距离为的点为，当圆心C在线段DE内部时，BC＞HC，且BC∈，从而当圆心C在线段DE内部时，圆C符合题意.考虑点C在直线HB的左侧，显然BC＞HC，在直线y=2上在HB左侧的到HB距离为的点为，在HB左侧的到B的距离为的点为，当圆心C在线段GT(不含点G)上时，圆C符合题意.

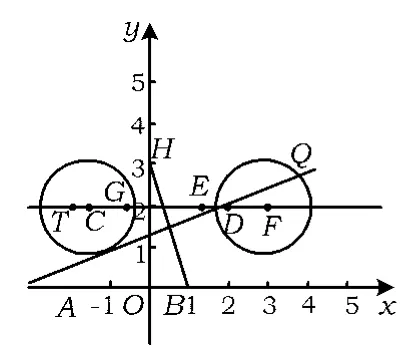
图3

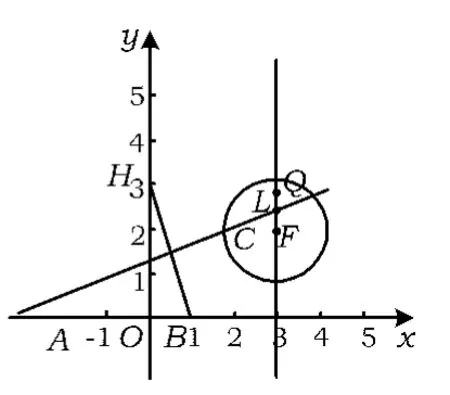
图4

变式3已知点B(1，0)，H(0，3)，C(2，s)，P为线段HB上任意一点，过点P作以C为圆心、以为半径的圆的割线PMN，与圆C交于点M，N.设M为PN的中点，则实数s 的取值范围是______.

分析易求HB的垂直平分线方程为，与x=3交于点.如图4，当圆心C位于点L的下方时，HC＞BC，由例1第3)小题的分析过程知F(3，2)是点C的最下方的位置，易知点L到HB的距离为，从而当圆心C在线段LF上时，圆C符合题意;当圆心C位于点L的下方时，HC＜BC，在直线x=3上位于L上方到点B的距离为的点为，当圆心C在线段QL上时，圆C符合题意.

变式4已知点B(1，0)，H(0，3)，C(t，s)，P为线段HB上任意一点，过点P作以C为圆心、以为半径的圆的割线PMN，与圆C交于点M，N.设M为PN的中点，则所有适合条件的圆心C的轨迹所构成的图形面积是______.

分析易求HB的垂直平分线RS的方程为，注意到如图5，分别以B， H为圆心、以为半径画圆，与RS交于点R，S.与BH平行且到BH的距离为的2条直线与靠近RS的2段弧交于点U，V，X，Y，形成2个封闭区域——线段UV，弧，线段VR构成一个封闭区域Ⅰ，线段XY，弧，线段YS构成另一个封闭区域Ⅱ，则圆C的圆心在2个封闭的区域中运动时符合题意.

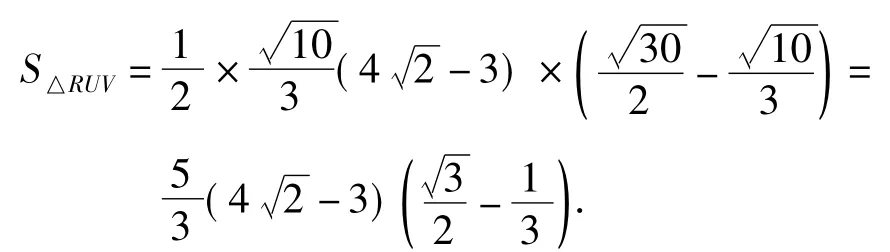
可以算出小弓形的面积为

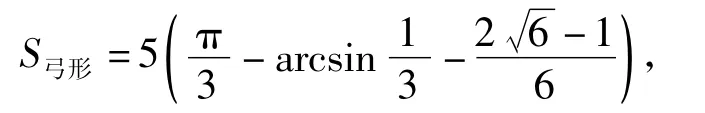
因此所求的轨迹面积为

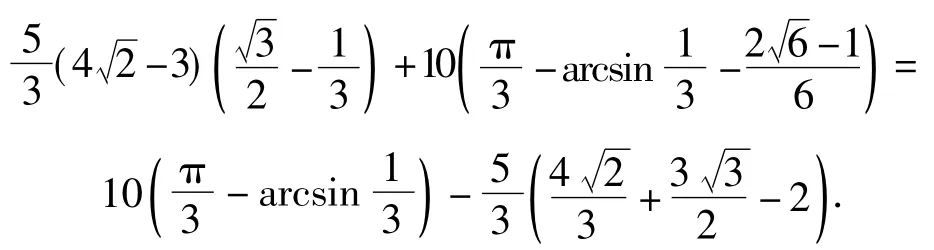
变式5已知点B(1，0)，H(0，3)，C(t，s)，P为线段HB上任意一点，过点P作以C为圆心、以为半径的圆的割线PMN，与圆C交于点M，N.设M为PN的中点，则所有适合条件的圆的轨迹所构成的图形面积是______.

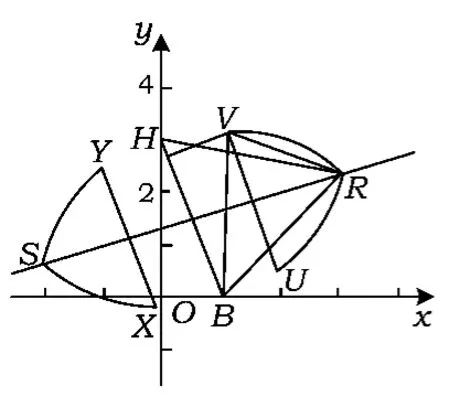
图5

图6

分析仿变式4得圆C的圆心在2个封闭的区域中运动时符合题意(如图5所示)，从而圆C的轨迹也为2个区域(如图6所示)，其中一个区域可划分为9个小区域:1个矩形、2个钝角扇形、2个扇环、1个三角形、1个小扇形、2个弓形，易得矩形的面积为，钝角扇形的面积为

变式6已知点B(1，0)，H(0，3)，C(3，2)，P为线段HB上任意一点，过点P作以C为圆心的圆的割线PMN，与圆C交于点M，N.设(其中λ＞0，λ为已知的数)，则圆C的半径的取值范围是______.

分析依题意得

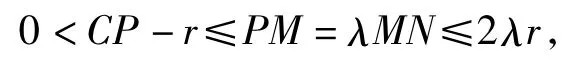
即r＜CP≤(2λ+1)r恒成立，从而

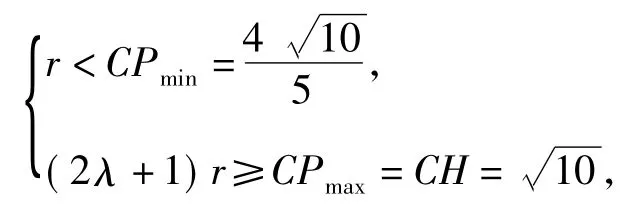
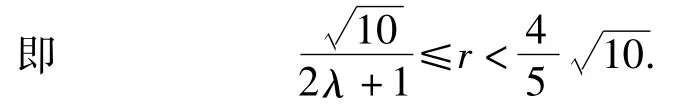
2 高考链接

例2如图7所示，为保护河上古桥OA，规划建一座新桥BC，同时设立一个圆形保护区.规划要求:新桥BC与河岸AB垂直;保护区的边界为圆心M在线段OA上并与BC相切的圆，且古桥2端O和A到该圆上任意一点的距离均不少于80 m.经测量，点A位于点O正北方向60 m处，点C位于点O正东方向170 m处(OC为河岸)，

1)求新桥BC的长;

2)当OM多长时，圆形保护区的面积最大?

(2014年江苏省数学高考试题第18题)

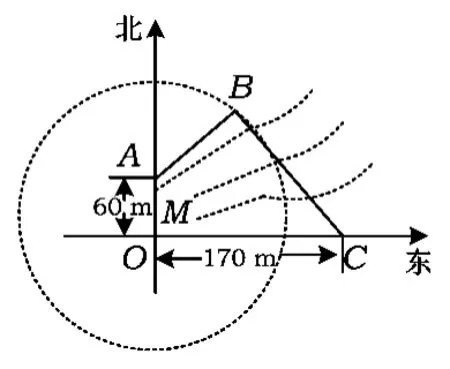
图7

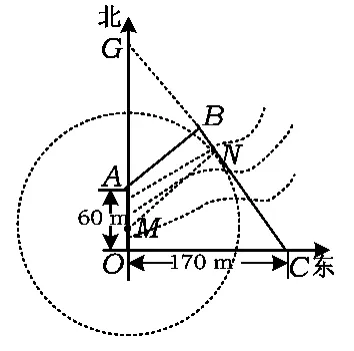
图8

分析1)以O为原点、正东方向为x轴正方向建立直角坐标系(如图8所示).由题意可知A(0，60)，B(170，0)，由可知直线BC的斜率，则直线BC的方程为

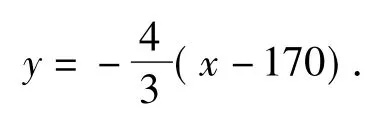
由AB⊥BC可知，AB所在的直线方程为

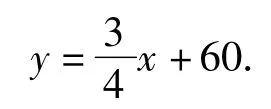
联立方程组

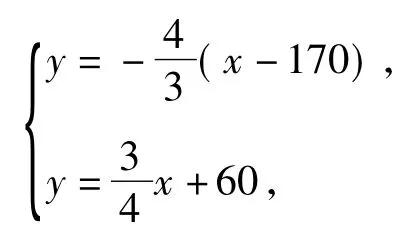
解得x=80，y=120，即点B(80，120)，故

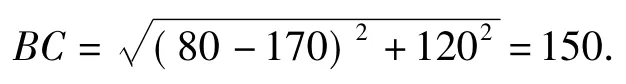
2)由题意设M(0，a)(其中0≤a≤60)，圆M的方程为

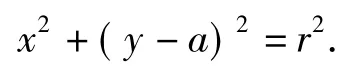
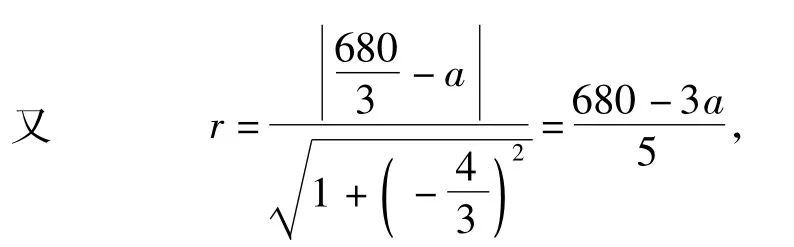
古桥2端O和A到该圆上任意一点的距离均不少于80 m，从而

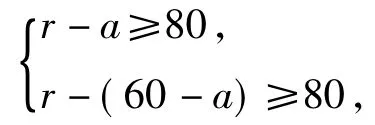
综上可知，当OM=10 m时，圆形保护区的面积最大，且最大值为16 900π.

例3设集合，其中x，y∈R}，B={(x，y)|2m≤x+y≤ 2m+1，其中x，y∈R}，若A∩B≠φ，则实数m的取值范围是______.

(2011年江苏省数学高考试题第14题)

分析当m≤0时，集合A是以(2，0)为圆心、以|m|为半径的圆，集合B是在2条平行线之间的点.因为，所以A∩B≠φ，此时无解.当m＞0时，集合A是以(2， 0)为圆心、以和|m|为半径的圆环，集合B是在2条平行线之间的点，则必有

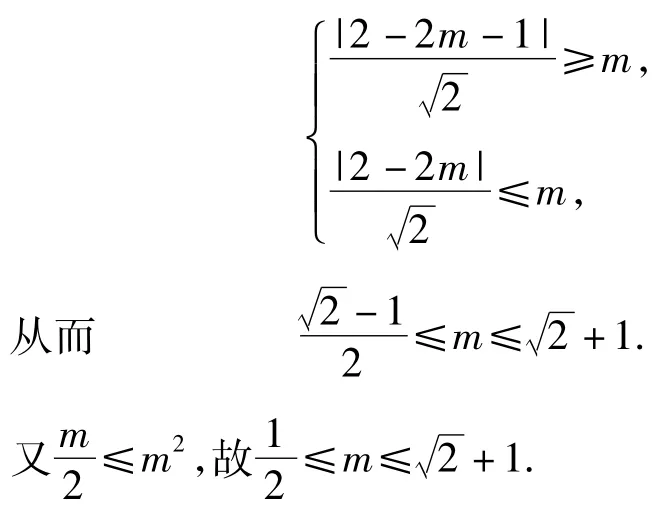
例4在平面直角坐标系xOy中，圆C的方程为x2+y2－8x+15=0，若直线y=kx－2上至少存在一点，使得以该点为圆心、1为半径的圆与圆C有公共点，则k 的最大值是______.

(2012年江苏省数学高考试题第12题)

分析圆C的方程可化为

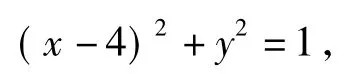
即圆C的圆心为(4，0)，半径为1.由题意，在直线y=kx－2上至少存在一点A(x0，kx0－2)，以该点为圆心、1为半径的圆与圆C有公共点，从而存在x0∈R，使得AC≤1+1成立，即

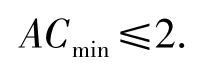
因为ACmin即为点C到直线y=kx－2的距离，所以，解得，故k的最大值是.

例5在平面直角坐标系xOy中，点A(0，3)，直线l:y=2x－4.设圆C的半径为1，圆心在l上.

1)若圆心C也在直线y=x－1上，过点A作圆C的切线，求切线的方程;

2)若圆C上存在点M，使MA=2MO，求圆心C的横坐标a的取值范围.

(2013年江苏省数学高考试题第17题)

分析1)由即C(3，2)，因此圆C的方程为

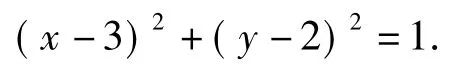
设过点A与圆C相切的直线方程为y=kx+3，由点到直线的距离公式得，解得k=0或.于是，所求切线的方程为y=3或.

2)设C(a，2a－4)，则圆C的方程为

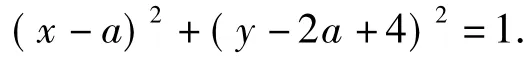
设M(x，y)，则由MA=2MO，得

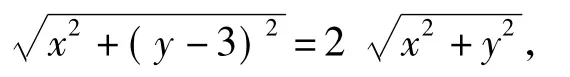
2边平方，整理得

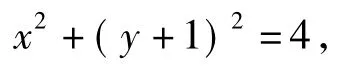
这是一个圆.该圆与圆C有公共点，从而

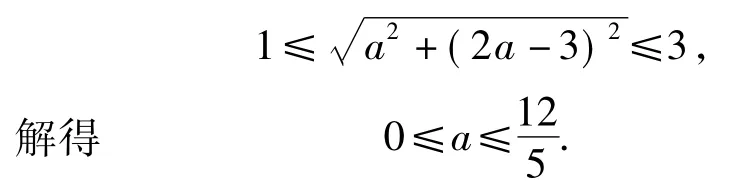
直线与圆的呈现千姿百态，其求解过程美不胜收，其答案寓繁于简.若再深层探究，则更美轮美奂，会让你进入另一个“仙景”——圆锥曲线.