对数学高考一题多空填空题命制的探讨
●曹凤山(余杭高级中学浙江杭州311100)
对数学高考一题多空填空题命制的探讨
●曹凤山(余杭高级中学浙江杭州311100)
填空题被称为数学高考命题的“试验田”,其命题形式、内容等方面都处在不断变革和完善之中,一题多空是命题技术创新的形式之一.2004年北京市数学高考试卷中开始出现一题两空,一些省市(如湖南、湖北、广东、天津等)相继引入这种题型.
1 一题多空是对填空题题型功能的进一步优化与完善
填空题通过提供一个不完整的叙述,让考生根据要求填写空缺的部分(定量或者定性),形成一个正确的命题,填写内容可以是条件,也可以是结论,命题形式比较灵活,主要考查基本概念、基本技能.
填空题与选择题同属客观题,题型的特点与功能都很突出.如试题形式简洁,考查针对性强、单题立意鲜明;评分客观、快捷,定量化的试题还可以考虑计算机辅助阅卷;单题知识点有效控制,一组试题又有比较理想的知识覆盖率等.
相比选择题,填空题没有备选项,既没有提示,又避免了干扰,能更真实地反映学生的客观水平,显示出这种题型在考查双基方面的优势.相对于解答题,由于不显示解题步骤,没有过程分,一笔失误与根本不会的结果没有任何区别,填空题也成为考生最头疼的题型之一,得分率相对较低,区分度也受到一定影响.另外,一题一空的填空形式,命题时考查的知识点数量与考查深度必须严格控制,如求解的过程宜短,不宜超过3步,否则难以保证信度,也势必降低区分度.一题多空形式在发挥一题一空题型优势的同时,设立“中间站”,体现局部结果,部分弥补了填空题的不足:一方面可以增加考查内容,扩大知识覆盖面,一个主题下分解成2个(或者更多)答题点,考查更多的双基,考生可以更加“知无不言”,避免没有步骤造成考生一笔写错,整体失分,更真实地反映客观水平;另一方面,对于难度较大的试题,一些学生“分步得分”,体现考生之间的差异,在送出一定分数的基础上,提高一些试题的考查深度,既丰富了命题形式,又可以提高试卷的区分度,从而更好地完成高考在人才选拔中的任务.
2 一题多空填空题的数量、试题位置及评分标准丰富了试卷模式
整卷整体在布局,单题重在立意.由于没有选择项提示,在解法上,填空题直接求解较多,一些间接方法的使用远不如选择题有效、准确,解题速度明显低于选择题.在一张试卷中填空题的数量要充分考虑考生的实际,合理安排,使用太多会给考生造成心理负担,使用过少则不能显示其在调整区分度、体现选拔等方面的作用.
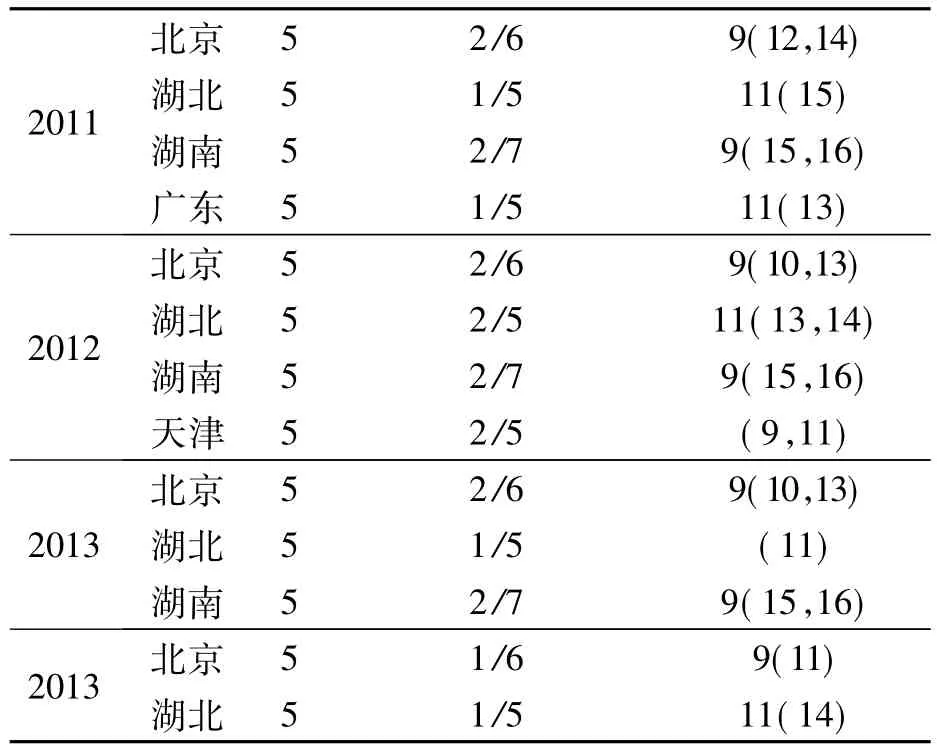
续表1
从表1可以看出:各省市使用一题多空(基本都是一题两空)试题的数量都不一样,同一省市不同年份的试卷中试题数量也有区别;从试题位置来看,同样不固定,根据选材、内容等特点,灵活摆放其位置,命题人一般根据素材的类型和难度预设、预估,按照难度次序从易到难排列,有些与一题一空混合排列,有些则集中出现,没有固定次序.试卷模式每年都可能有变化,打破“八股”模式,灵活构筑令人耳目一新的高考试卷.
从评分的角度看,一题多空丰富了评分模式.如一些省份一道一题两空(共5分)的选择题,根据试题难度、考查目的、功能定位等,可以前空2分后空3分,或者前空3分后空2分,或者只对一空得2分、2空都对得5分,更客观地体现了“按劳取酬、优工优酬、体现侧重”的原则.
3 一题多空填空题的设计示例
在一题一空填空题的基础上,一题多空试题设计形式更加多样.根据不同的分类标准分为不同的类型,当然,这些分类不是绝对的,没有绝对的零点、分界线.
3.1 从考查目的看
可以分为概念型、计算型、推理型以及阅读理解型等.概念型填空题,一般是通过实例检测学生对数学概念的理解是否正确,一题多空可以在一个主干知识下考查几个相关的知识点,使主干知识的考查更加突出,避免蜻蜓点水式的点到为止.同样,计算型填空题通过一些运算,检测对算理、公式、性质的理解和运算的准确性,一题多空可以有简单的计算,也可以有一定程度的推演与算理考查;推理型填空题主要通过推理能力的训练与考查,检测学生是否熟练掌握推理能力,是否熟练掌握相关的数学基本性质,一题多空一般前特殊后一般,步步推进;阅读理解型又称新定义问题,通过给出的材料“命题作文”,一题多空可以更真实地反映考生的阅读理解以及进一步学习的潜能.
例1已知双曲线的离心率为2,焦点与椭圆的焦点相同,那么双曲线的焦点坐标为______,渐近线方程为______.
(2010年北京市数学高考试题第13题)
分析本题属概念型问题.主要考查双曲线离心率、焦点、渐近线、椭圆的焦点等基本概念,基本没有计算量,体现“会即对”的特点.双曲线焦点即为椭圆焦点,不难算出焦点坐标为(±4,0),又双曲线的离心率为2,即,c=4,故a=2,,渐近线方程为
类题再现从某小学随机抽取100名学生,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如图1所示).由图1中的数据可知a= ______.若要从身高在[120,130),[130,140),[140,150]这3组内的学生中,用分层抽样的方法选取18人参加一项活动,则从身高在[140,150]内的学生中选取的人数应为______(答案:0.030,3).
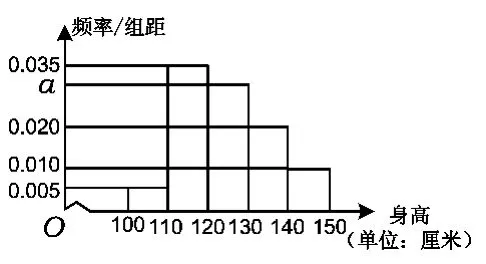
图1
(2010年北京市数学高考试题第11题)
例2设f(x)是定义在(0,+∞)上的函数,且f(x)>0.对任意a>0,b>0,若经过点(a,f(a)),(b,-f(b))的直线与x轴的交点为(c,0),则称c为a,b关于函数f(x)的平均数,记为Mf(a,b).例如,当f(x)=1(其中x>0)时,可得,即Mf(a,b)为a,b的算术平均数.
1)当f(x)=______(其中x>0)时,Mf(a,b)为a,b的几何平均数;
2)当f(x)=______(其中x>0)时,Mf(a,b)为a,b的调和平均数
(以上2空各只需写出1个符合要求的函数即可.)
(2014年湖北省数学高考试题第14题)
分析本题属于阅读理解型(新定义),这类问题常出现教材中没有学过的一些概念、运算、符号,要求考生读懂题意并结合已有的知识加以理解,根据新定义进行运算、推理.阅读理解型问题一般文字叙述较长,信息量较大,各种关系错综复杂,考查的知识也灵活多样,既考查学生的阅读能力,又考查学生的解题能力等.如果一题一空则显得题干大而无当,利用率太低,一题两空可以充分显示考生的理解深度.
本题中,定义了c为a,b关于函数f(x)的平均数,实际上本题还考查了直线的相关知识.同时,试题结论呈现开放性,考生可以根据自己的理解与熟练程度选择不同的函数形式.过点(a,f(a)),(b,-f(b))的直线的方程为

类题再现回文数是指从左到右读与从右到左读都一样的正整数.如22,121,3 443,94 249等.显然2位回文数有9个:11,22,33,…,99,3位回文数有90个:101,111,121,…,191,202,…,999,则
1)4位回文数有______个;
2)2n+1(n∈N+)位回文数有______个.
(答案:90,9×10n.)
(2012年湖北省数学高考试题第13题)
例3已知离散型随机变量X的分布列如图2所示.若EX=1,DX=1,则a= ______,b =______.

图2
(2009年广东省数学高考试题第12题)
分析本题属于计算型问题.主要考查利用离散型随机变量的分布列、方差、数学期望的相应公式与性质,通过建立方程组,求解方程组解决问题,显示了一个完整的问题形式.由题意知

(2011年北京市数学高考试题第11题)
例4如图3放置的边长为1的正方形PABC沿x轴滚动.设顶点P(x,y)的轨迹方程是y=f(x),则f(x)的最小正周期为______;y=f(x)在其2个相邻零点间的图像与x轴所围区域的面积为______.
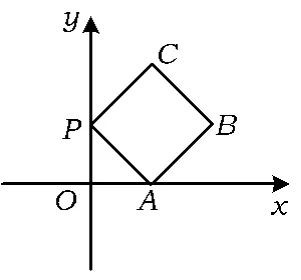
图3
(2010年北京市数学高考试题第14题)
说明“正方形PABC沿x轴滚动”包括沿x轴正方向和沿x轴负方向滚动.沿x轴正方向滚动指的是先以顶点A为中心顺时针旋转,当顶点B落在x轴上时,再以顶点B为中心顺时针旋转,如此继续.类似地,正方形PABC可以沿x轴负方向滚动.
分析本题属于探索型问题.探索型问题可以是条件探索型,也可以是结论探索型,或者存在型.与阅读理解问题类似,一题多空有利于题目设计的完整性、考查的深刻性.
不难想象,从某一个顶点(比如点A)落在x轴上时开始计算,到下一次点A落在x轴上,这个过程中4个顶点依次落在了x轴上,而每2个顶点间距离为正方形的边长1,因此该函数的周期为4.
下面考察点P的运动轨迹.不妨考察正方形向右滚动,点P从x轴上开始运动的时候,首先是围绕点A运动(轨迹是一个圆),该圆半径为1;然后以点B为中心,滚动到点C落地,期间是以BP为半径,旋转90°;然后以点C为圆心,再旋转90°,这时候的圆以CP为半径,因此最终构成图像如图4所示:

图4
因此不难算出这块区域的面积为π+1.
类题再现设N=2n(其中n∈N*,n≥2),将N个数x1,x2,…,xN依次放入编号为1,2,…,N的N个位置,得到排列P0=x1x2…xN.将该排列中分别位于奇数与偶数位置的数取出,并按原顺序依次放入对应的前个位置,得到排列P1=x1x3…xN-1x2x4…xN,将此操作称为C变换,将P1分成2段,每段个数,并对每段作C变换,得到P2;当 2≤i≤n-2时,将Pi分成2i段,每段个数,并对每段作C变换,得到Pi+1.例如,当N=8时,P2= x1x5x3x7x2x6x4x8,此时x7位于P2中的第4个位置.
1)当N=16时,x7位于P2中的第______个位置;
2)当N=2n(其中n≥8)时,x173位于P4中的第______个位置.
(答案:6,3×2n-4+11.)
(2012年湖南省数学高考试题第16题)
3.2 从层次结构看
可以分为并列型、递进型.并列型的多空问题之间知识内容、思维层次没有前后关系,各自独立求解,只是增加考查知识的覆盖面;递进型,前一空的解决是后一空解决的必需,第1空的解决为第2空作铺垫,难度拾阶而上,既有区分度又让一些学生得到部分分数.
例5如图5,双曲线(其中a>0, b>0)的2个顶点为A1,A2,虚轴2个端点为B1,B2,2个焦点为F1,F2.若以A1A2为直径的圆内切于菱形F1B1F2B2,切点分别为A,B,C,D,则
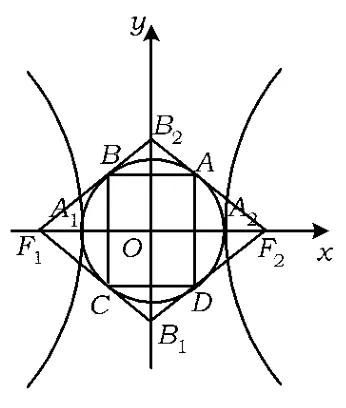
图5
1)双曲线的离心率e= ______;
2)菱形F1B1F2B2的面积S1与矩形ABCD的面积S2的比值=______.
(2012年湖北省数学高考试题第14题)
分析本题属于递进型问题.主要考查双曲线中离心率及实轴虚轴的相关定义,以及一般平面几何图形的面积计算.其中,第2空的解决要依靠第1空的结果.
1)由于以A1A2为直径的圆内切于菱形F1B1F2B2,因此点O到直线F2B2的距离为a,又由于虚轴2个端点为B1,B2,因此OB2的长为b.在△F2OB2中,由三角形的面积公式知
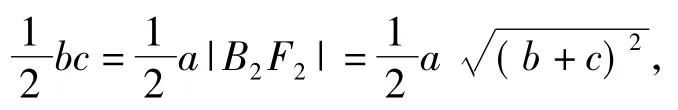
又c2=a2+b2,联立可得
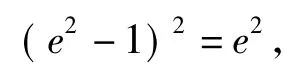
2)设∠F2OB2=θ,显然∠F2A2O=∠AOB2=θ,因此
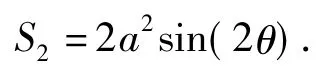
在△F2OB2中,求得

菱形F1B1F2B2的面积S1=2bc,再根据第1)小题中求得的e值可以得出
类题再现椭圆的焦点为F1,F2,点P在椭圆上,若|PF1|=4,则|PF2|=______;∠F1PF2的大小为______(答案:2,120°).
(2009年北京市数学高考试题第12题)
例6已知正方形ABCD的边长为1,点E是AB边上的动点,则的值为______的最大值为______.
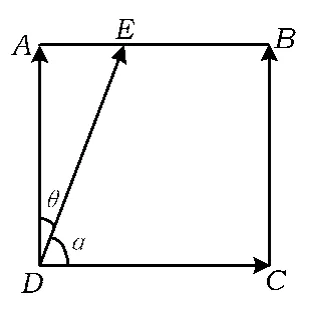
图6
(2012年北京市数学高考试题第13题)
分析本题属于并列型问题,2个问题同一题干,前后没有因果关系,可以独自求解,难度上一般是依次递增.根据平面向量的数量积公式

类题再现已知数列{an}满足:a4n-3=1,a4n-1=0,a2n=an(其中n∈N*),则a2009= ______,a2014=______(答案:1,0).
(2009年北京市数学高考试题第14题)
对于一题多空填空题的求解,与一题一空类似,主要是采用直接推演,即由因导果法,它是解填空题的基本方法.根据填空题的题设条件,通过定义、公理、定理、公式等经过计算、变形、分析、推理或判断,得出正确的结论.只是一题多空要注意前后填写内容之间的逻辑关系,采取分步得分、跳步得分、阶梯得分等策略,当然,在一定条件下,也要注意特殊化方法、数形结合方法等特殊解法的运用.
[1]教育部考试中心.高考数学测量理论与实践[M].北京:高等教育出版社,2005.
[2]曹凤山,赵冬梅.高考数学试题是如何考查继续学习潜能的[J].中学数学教学参考:上旬,2011(11):45-48.

