花开也有声——数列的单调性问题

●胡东芳(浦江中学浙江浦江322200)

花开也有声
——数列的单调性问题

●胡东芳(浦江中学浙江浦江322200)

数列是高中数学的重要内容，又是学习高等数学的基础，是高考的重点内容之一.数列与其他知识结合，包括数列与函数、方程、不等式、几何等的结合，是高考中的难点也是热点.尤其是数列的单调性问题，在高考中频频亮相.

数列是一类特殊的函数，其定义域只能取正整数集或其有限子集，因此在处理数列的单调性问题时，可以考查数列前后2项的关系，也可以通过构造函数来处理.

类型1直接判断单调性问题

例1已知函数f(x)=log2x－logx2(其中0＜x＜1)，数列{an}满足f(2an)=2n(其中n∈N*).

1)求数列{an}的通项公式;

2)判断数列{an}的单调性.

评注数列单调性问题的刻画方式:1)考查前后2项的大小关系，例1用的是作商比较;2)构造函数，利用函数的单调性.

例2已知数列{an}的通项公式是an=n2+ kn+2，且数列{an}为递增数列，求实数k的取值范围.

分析本题学生容易产生的错解是构造函数f(x)=x2+kx+2，由数列{an}为递增数列得函数f(x)在［1，+∞)上递增，得出，解得k≥－2.

事实上，由数列{an}为递增数列得an+1－an＞0，即

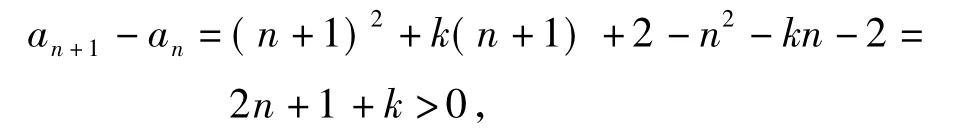
得k＞－3.

评注本题考查前后2项的大小关系，例1用的是作商比较，而例2用的是作差比较.例2若用函数单调性求解，则应注意需与比较，而不是与1比较.

例3已知数列{an}的各项均为正数，其前n项和记为Sn，且数列{an}满足

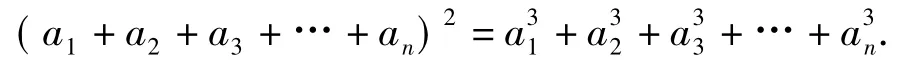
1)求数列{an}的通项公式;

分析1本题第2)小题考查数列的单调性问题.若构造函数，则要考查的是复合函数，当然也可以直接考查bn+1＞bn.

1)由a1+a2+a3+…+an=Sn和已知条件得

因为数列{an}的各项均为正数，所以

分析求正整数k，使得对任意n∈N*均有Sk≥Sn，其实质上是求{Sn}的最值问题.最值问题的求解可通过刻画数列{Sn}的单调性完成，而刻画{Sn}的单调性问题即考查{cn}各项的正负.

所以当n≥5时，cn＜0.

综上可得，对任意n∈N*均有S4≥Sn，故k=4.

例6已知首项为的等比数列{an}不是递减数列，其前n项和为Sn(其中n∈N*)，且S3+ a3，S5+a5，S4+a4成等差数列.

1)求数列{an}的通项公式;

(2013年天津市数学高考理科试题第19题)

分析{Tn}可以看成关于Sn单调递增的函数，故只要求Sn的最大项和最小项.

1)设等比数列{an}的公比为q，因为S3+a3，S5+a5，S4+a4成等差数列，所以

评注数列与函数有密切联系，求数列中的最大项与最小项，可以利用函数图像或者数列的单调性求解，同时注意数列的单调性与函数单调性的区别.

类型3数列中的恒成立问题

例7已知an=n，是否存在正数M，使不等式对一切n∈N*成立?若存在，求出M的取值范围;若不存在，请说明理由.

分析本题看起来很复杂，恒成立问题可以使用分离参数的方法转化为最值问题.

假设存在满足条件的M，即

评注本题转化为g(n)的单调性，且g(n)的式子是连乘积因式，用作商比较来判断.

评注本题是非常典型的应用函数的单调性得出数列的和，继而进行比较大小的综合应用问题，对考生的考查是全方位的.

2014年浙江省数学高考理科卷的最后一题考查的正是数列的综合应用，花开也有声，让我们共同期待新课程改革背景下2015年高考数列问题的走势.