一类非线性矩阵方程对称解的双迭代算法①

程可欣，彭振赟

（桂林电子科技大学 数学与计算科学学院，广西 桂林 541004）

非线性矩阵方程

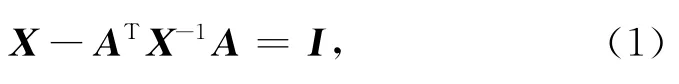
其中A，X∈Rn×n，在结构动力学、振动理论、自动控制理论等领域具有广泛的应用，得到了国内外专家、学者的广泛关注。文献［1］研究了矩阵方程（1）有正定解的充分必要条件，并提出求解的有效算法。文献［2］应用直接法求解矩阵方程（1），并给出方程有正定解的充分必要条件。文献［3］研究了矩阵方程X＝Q＋NX－1N＊正定解的迭代算法。文献［4］研究了求解方程X＋A＊X－1A＝I和X－A＊X－1A＝I的极值解的不动点迭代法和牛顿法迭代算法。文献［5］给出了求解矩阵方程X＋A＊X－αA＝Q的最大对称正定解的不动点迭代法，并讨论了算法的收敛性问题。文献［6］给出了矩阵方程X＝Q＋AH（I⊗X－C）－1A的等价形式及求解的牛顿迭代解法。

近年来，形如方程（1）的矩阵方程的求解方法研究虽然取得了很多的研究成果，但关于此类非线性矩阵方程对称解的求解方法的研究却不是很多。为此，运用牛顿迭代解法求解非线性矩阵方程（1）的对称解，然后对牛顿法每一步迭代所计算出的线性矩阵方程应用修正共轭梯度法（MCG）［7－10］，求得它的对称解或最小二乘对称解，从而建立求解方程（1）对称解的双迭代算法。

1 牛顿迭代解法

记Rn×n为n×n阶矩阵的集合，SRn×n为n×n阶实对称矩阵的集合，I为n×n阶单位矩阵，AT为矩阵A的转置，‖A‖为矩阵A的Frobenius范数。

引入矩阵函数：

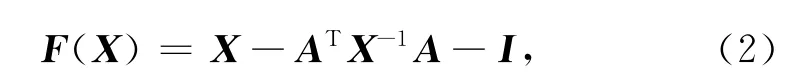
则求解矩阵方程（1）的解等价于求解方程F（X）＝0的解。矩阵函数F（X）在X处方向为E的Fréchet导数为

因此，牛顿法求解非线性矩阵方程（1）的迭代格式可描述为算法1。

算法1 牛顿法求矩阵方程（1）的迭代格式。

1）给出初始矩阵X0＝I，误差容许值ε＞0，令k∶＝0。

2）若‖F（Xk）‖≤ε，则停止；否则，求Ek∈SRn×n，使得

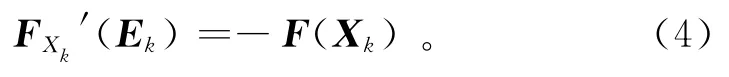
3）计算Xk＋1＝Xk＋Ek。

4）置k∶＝k＋1，转步骤2）。

类似于文献［11－12］中关于牛顿迭代法求非线性矩阵方程的收敛性结论的证明，易证如下结论成立：假设X＊是方程（1）的零点，且取初始矩阵X0＝I，则由算法1生成的矩阵序列｛Xk｝收敛于X＊。此外，牛顿法的关键是求解线性矩阵方程（4），但由于截断误差的存在，对牛顿法中的某个迭代步k，矩阵方程（4）可能没有解Ek∈SRn×n，此时可通过求它的最小二乘解∈SRn×n代替，这也是双迭代算法的一个特点。

2 MCG迭代解法

矩阵方程（4）等价于

其中：

问题1 若矩阵方程（5）有解E∈SRn×n，求E∈SRn×n使得矩阵方程（5）成立。

问题2 若矩阵方程（5）无解E∈SRn×n，求~E∈SRn×n，使得

2.1 问题1的MCG迭代算法

算法2 MCG法求矩阵方程（5）的迭代格式。

1）任意给定初始矩阵E1∈SRn×n，置k∶＝1，计算：

2）若Rk＝0，或者Rk≠0且Qk＝0，则停止计算，否则，计算

3）计算：

4）置k∶＝k＋1，转步骤2）。

由文献［7］的算法收敛性证明，可得算法2的收敛性结果（定理1）。

定理1 对任意初始矩阵E1∈SRn×n，若矩阵方程（5）有对称解，则算法2可在有限步计算后求得矩阵方程（5）的一个对称解；若取初始矩阵E1满足

其中H∈Rn×n，特别地，取E1＝0∈SRn×n，则算法2可在有限步计算后，得到矩阵方程（5）的唯一极小范数对称解；若矩阵方程（5）无对称解，则它的充要条件是迭代过程中存在正整数k，可由算法2得到Rk≠0，Qk＝0。

2.2 问题2的MCG迭代算法

在算法2中，当Rk≠0，Qk＝0时，算法中断，即问题1无该类对称解，则此时对问题迭代步2）有如下结论成立。

定理2 求满足问题2的对称最小二乘解等价于求矩阵方程（5）的非对称解＾E，即求

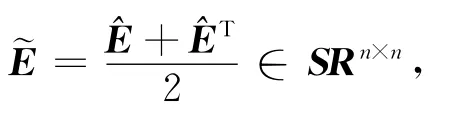
使得

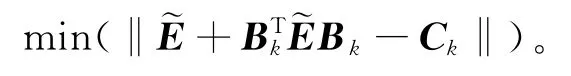
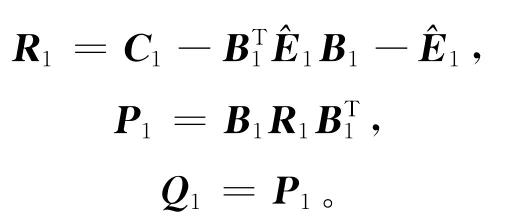
2）若Rk＝0，则计算

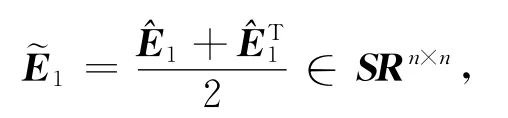
停止计算；否则，计算：

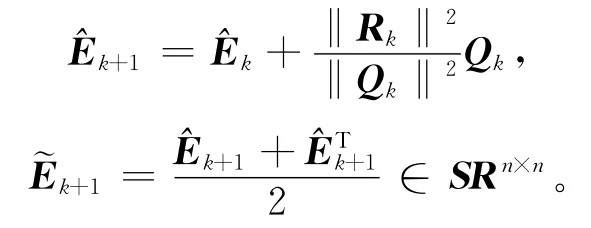
3）计算：

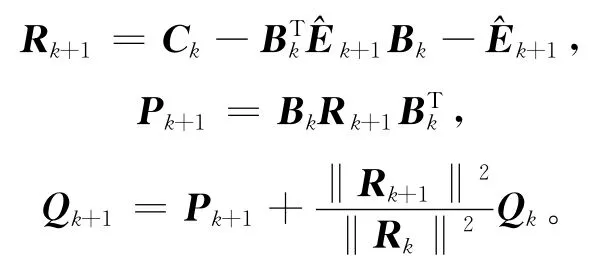
4）置k∶＝k＋1，转步骤2）。

由文献［10］可知，算法3有如下收敛性结论：

定理3 对任意初始矩阵∈Rn×n，算法3可在有限步计算后，求得矩阵方程（5）的一个一般解，从而可得的最小二乘对称解。若取初始矩阵

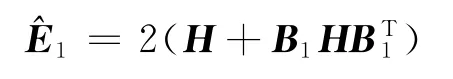
其中H∈Rn×n，特别地，取＝0∈SRn×n，则算法3可在有限步计算后，得到的唯一极小范数对称解，也即矩阵方程（5）的唯一极小范数最小二乘对称解。

2.3 求非线性方程（1）对称解的双迭代算法

算法4 双迭代法求矩阵函数（2）的零点迭代格式。

1）给定初始矩阵E1∈SRn×n，置k∶＝1。

2）若‖F（Xk）‖＝0，则停止计算，否则，转算法2，求Ek∈SRn×n，使得矩阵方程（5）成立；若算法2中断，则转算法3，求∈SRn×n，使得

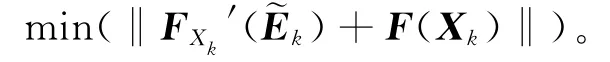
3）计算：

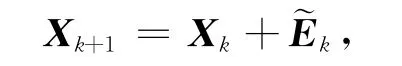
k∶＝k＋1，转步骤2）。

因方程（2）是矩阵方程（1）的矩阵函数，从而可知求解矩阵方程（1）对称解的双迭代算法。算法的收敛性由算法1、2、3的收敛性确定。

3 数值实例

给定矩阵A：

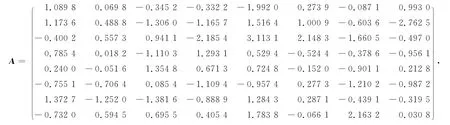
则由文献［2］中的定理知，矩阵方程（1）有正定 解，按算法4迭代118步，得矩阵方程（1）的解为：

由此可得，

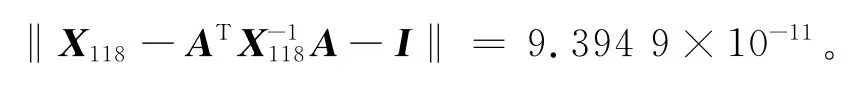
4 结束语

通过给出求解非线性矩阵方程X－ATX－1A＝I的牛顿迭代格式，求出该矩阵方程的对称解，再应用修正共轭梯度法求解由牛顿法每一步迭代所得到的线性矩阵方程对称解，从而建立了求解此类非线性矩阵方程对称解的双迭代算法。数值例子证实了双迭代算法的有效性。

［1］Engwerda J C.On the existence of a positive definite solution of the matrix equationX＋ATX－1A＝I［J］.Linear Algebra and its Applications，1993，194：91－108.

［2］Zhan Xingzhi，Xie Jianjun.On the matrix equationX＋ATX－1A＝I［J］.Linear Algebra and its Applications，1996，247：337－345.

［3］Ferrante A，Levy B C.Hermitian solutions of the equationX＝Q＋NX－1N＊［J］.Linear Algebra and its Applications，1996，247：359－373.

［4］Meini B.Efficient computation of the extreme solutions ofX＋A＊X－1A＝QandX－A＊X－1A＝Q［J］.Mathematics of Computation，2002，71：1189－1204.

［5］Peng Zhenyun，EI－sayed S M，Zhang Xianglin.Iterative methods for the extremal positive definite solution of the matrix equationX＋A＊X－αA＝Q［J］.Journal of Computational and Applied Mathematics，2007，200：520－527.

［6］Liu Panpan，Zhang Shugong.Newton’s method for solving a class of nonlinear matrix equations［J］.Journal of Computational and Applied Mathematics，2014，256：254－267.

［7］彭亚新.求解约束矩阵方程及其最佳逼近的迭代法的研究［D］.长沙：湖南大学，2004：63－69.

［8］彭卓华，胡炎锡，张磊.矩阵方程A1X1B1＋…＋AlXlBl＝C的中心对称解及其最佳逼近［J］.数学物理学报：A辑，2009，29（1）：193－207.

［9］李书连，张凯院，刘晓敏.一类矩阵方程异类约束解与Ls解的迭代算法［J］.高效应用数学学报，2012，27（3）：313－324.

［10］徐树方.矩阵计算的理论与方法［M］.北京：北京大学出版社，1995：142－155.

［11］Long Jianhui，Hu Xiyan，Zhang Lei.Improved Newton’s method with eact line searches to solve quadratic matrix equation［J］.Journal of Computational and Applied Mathematics，2008，222：645－654.

［12］龙建辉，胡锡炎，张磊.最速下降法求解二次矩阵方程［J］.湖南大学学报：自然科学版，2008，35（4）：85－88.