NURBS曲线矩阵表示及其在插补中的应用①

徐水龙，徐周波，古天龙

（1.桂林电子科技大学 机电工程学院，广西 桂林 541004；2.桂林电子科技大学 计算机科学与工程学院，广西 桂林 541004）

随着计算机辅助图形设计理论的发展，非均匀有理B样 条（non－uniform rational B－spline，简 称NURBS）技术以其独特的优点，从众多形状描述曲线曲面中脱颖而出，成为定义工业产品几何形状的唯一数学方法，并被广泛应用于CAD／CAM中［1］。但由于控制算法的不足及CPU处理能力的限制，NURBS技术在CAM中的应用不尽人意，其中NURBS曲线曲面的表示问题显得尤为突出。

在NURBS曲线曲面插补中，为完成一维参数空间到三维坐标空间的映射，需计算大量插补点的坐标；同时为了控制刀具的速度，需对曲线上各点的曲率进行计算。传统的Deboor算法［2］在求解NURBS曲线上点的坐标和导数的递推过程中存在大量的重复计算，从而增加了许多额外的时间开销。近年来，矩阵理论的发展和计算机对矩阵运算处理水平的提高，使得NURBS的矩阵表示算法越来越受到国内外学者的重视。Choi等［3］和王学福等［4］均提出了用于计算NURBS曲线的符号矩阵表示算法，但都未给出任意阶NURBS曲线显式矩阵表达式的递推过程。Grabowski等［5］给出了B样条基的系数矩阵元素间的递推公式，但并没有给出系数矩阵的矩阵递推公式。秦开怀［6］采用Toeplitz矩阵，导出了任意阶NURBS曲线的显式矩阵递推公式，但该公式中所含的矩阵相乘运算将增加乘法的计算量，且算法不易于用代码实现。潘日晶等［7］引入差商的概念，提出了NURBS曲线的显式矩阵表示算法，但该算法的推导过程较为繁琐，时间复杂性随NURBS曲线阶数的增加而大大增加，不利于保证直接插补的实时性。王国勋等［8］通过对B样条的导数公式进行逐阶积分，给出了系数矩阵的元素递推关系，但该递推关系分类复杂，同样不利于用代码实现。

鉴于此，基于文献［5］提出一种新型的系数矩阵递推公式。该算法具有计算量小、计算稳定、易于用代码实现等优点，可用于任意阶NURBS曲线和B样条曲线的矩阵表示及其升阶、降阶。在NURBS曲线直接插补可通过该算法进行预处理，求出曲线的系数矩阵并存储，便于后续轨迹规划和速度控制时直接调用该系数矩阵进行曲线求值求导，从而保证了插补的实时性。

1 NURBS曲线的矩阵表示形式

1.1 B样条曲线的表示式

k次B样条曲线的表示式为：

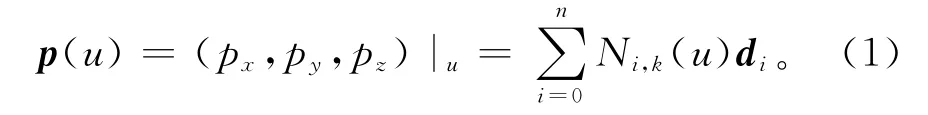
其中：u∈［0，1］；di＝（xi，yi，zi），i＝0，1，…，n为曲线的控制顶点；Ni，k（u）为由节点矢量U根据Deboor－Cox递推公式（式（2））决定的k次规范B样条基函数，简称B样条基。节点矢量U＝［u0，u1，…，un＋k＋1］，0≤ui≤1且ui≤ui＋1是经过规范化处理［7］的节点矢量。

根据B样条基的局部支承性，即当u∈［ui，ui＋1）时，有

于是可通过判断参数u所处区间，对曲线进行分段处理。故式（1）可写成如下分段形式：

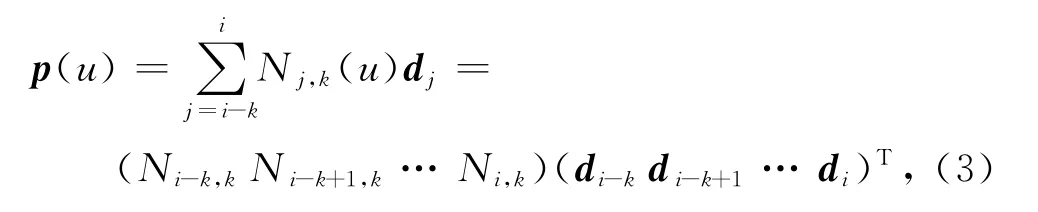
其中，由于任意l次B样条基u∈［ui，ui＋1）可展开成如下幂级数形式：

其中：（i）（与参数u无关，但与i有关）为l次B样条基Ni－h，l中uj项的系数；l＝1，2，…，k；h＝l，l－1，…，0；j＝0，1，…l。

记

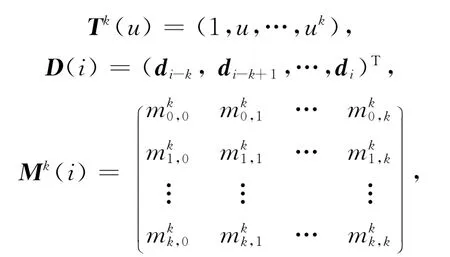
则式（3）可写成

其中，（k＋1）×（k＋1）阶矩阵Mk（i）称为k次B样条基的系数矩阵。

1.2 NURBS曲线的表示式

由于专门用于自由型曲线曲面设计的B样条方法无法满足构造初等曲线曲面的要求，于是学者们对B样条方法进行改进，提出了非均匀有理B样条（NURBS）方法。k次NURBS曲线C（u）的表达式

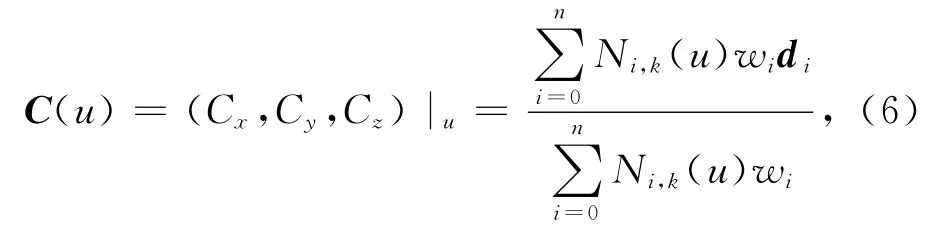
其中u∈［0，1］，wi（i＝0，1，…，n）称为权因子，其他各量的含义与式（1）相同。由式（6）可知，当wi＝1时，NURBS曲线便成为一条B样条曲线。基于式（5）的推导过程，式（6）可写成如下矩阵形式：

其 中：Q（i）＝（wi－kdi－k，wi－k＋1di－k＋1，…，widi）T；W（i）＝（wi－k，wi－k＋1，…，wi）T；u∈［ui，ui＋1）。

2 系数矩阵的递推算法

由式（7）可见，k次NURBS曲线的矩阵表示的关键是求其系数矩阵Mk（i）。文献［5］基于式（2）给出了系数矩阵元素的递推关系式，从关系式中可看出，每个高阶元素由4项低阶元素的加权项相加而得。但在递推过程中，这些加权项的权系数存在重复计算，且在计算系数矩阵中位于矩阵边缘的元素时，需要判断这4个加权项中是否含有为0的项。为弥补上述不足，通过对该递推关系式中的权系数进行变量代换，进一步对得到的关系式进行形式变换，找出某一低阶系数矩阵元素对哪些高阶系数矩阵元素中的哪些项有影响，提取受影响的项并组合叠加，最终推导出系数矩阵显式递推公式。

2.1 系数矩阵显式递推过程的推导

当u∈［ui，ui＋1）时，令 式（4）中＝ui－h＋l－为变量代换后的权系数。由此可得：＝1－；则根据式（2）有：

结合式（4）、（8）并展开可得

其中：l＝1，2，…，k；h＝l，l－1，…，0；j＝0，1，…，l。

将式（9）两边进行多项式展开，由等式两边含uj项的系数对应相等，可得递推关系：

其中

1）u∈［ui，ui＋1），＝1；

2）当j＝0时，

3）当j＝l时，

4）当h＝0时，

5）当h＝l时

为进一步得出系数矩阵的直接显式递推公式，对式（10）作如下形式变换：

式（11）～（14）中，p、q＝0，1，…，l－1；l＝1，2，…，k。

从上可看出，l－1次B样条基系数矩阵中的元素，仅对l次B样条基系数矩阵中的、产生影响，于是可提取式（11）～（14）中包含的项。最后将系数矩阵Ml－1（i）中的各个元素对系数矩阵Ml（i）中元素的影响进行组合叠加，可得u∈［ui，ui＋1）时Ml（i）的显式递推公式：

其中：

1）右边的矩阵中其余元素均为0；

2）＝1；

6）p、q＝0，1，…，l－1；l＝1，2，…，k。

从式（15）可看出，等式右边由l2个l＋1阶方阵相加，因而存在大量的加法运算，尤其是零加零的运算。为省去这些零加零运算，降低算法的时间复杂度，可作如下优化：先计算并存储对Ml（i）中各个元素的影响，再将对Ml（i）中各个元素的影响累加到先前存储的元素中，依此类推，便可递推出系数矩阵Ml（i）。

2.2 递推算法的代码实现

为实现上述算法，首先需要定义并初始化曲线的相关参数（曲线次数k、控制点个数n＋1、节点矢量U［n＋k＋2］）。将上述系数矩阵递推算法写成预处理函数，其C程序如下：

double M［k＋1］［k＋1］［k＋1］［n－2］＝0；

／／定义系数矩阵并初始化为0

void pretreat（）

｛

int p，q，L，i；

for（i＝0；i＜＝n－k；i＋＋）

｛／／对曲线分段处理

M［0］［0］［0］［i］＝1；

／／M［p］［q］［L］［i］即为文中的（i）

for（L＝1；L＜＝k；L＋＋）

｛for（q＝0；q＜＝L－1；q＋＋）

｛double beta，C，D；

beta＝U［i＋k＋q＋1］－U［i＋k＋q－L＋1］；

／／由于u0～uk均为0，故第i段曲线对应于

／／u∈［ui＋k，ui＋k＋1）

if（beta＝＝0）

｛C＝0； D＝0；｝

else

｛D＝－1／beta； C＝U［i＋k＋q＋1］／beta；｝

for（p＝0；p＜＝L－1；p＋＋）

｛double var1，var2；

／／定义2个中间变量，以减少重复计算

var1＝C＊M［p］［q］［L－1］［i］；

var2＝D＊M［p］［q］［L－1］［i］；

／／将式（15）中的各项用累加的方法表示，

／／以省去零加零运算

M［p］［q］［L］［i］＝M［p］［q］［L］［i］＋var1；

M［p］［q＋1］［L］［i］＝M［p］［q＋1］［L］［i］

＋M［p］［q］［L－1］［i］－var1；

M［p＋1］［q］［L］［i］＝M［p＋1］［q］［L］［i］

＋var2；

M［p＋1］［q＋1］［L］［i］＝M［p＋1］［q＋1］

［L］［i］－var2；

｝

｝

｝

｝

｝

由上可看出本算法的代码实现简单，过程清晰。而文献［6］的算法涉及矩阵的相关运算（如矩阵扩行、双对角矩阵的构造、矩阵相乘等），故代码实现将降低算法的执行效率。利用文献［8］的算法求系数矩阵中的元素，其递推公式分为5类，且递推公式需要调用同阶系数矩阵的元素，不利于编程实现和提高算法效率。综上所述，从代码实现角度分析，本算法具有明显优势。

3 算法效率的比较

设Tadd、Tsub、Tmul、Tdiv分别代表所需要的加、减、乘、除的运算次数，并假定它们满足如下关系：Tadd≈Tsub，Tmul≈Tdiv，Tmul≈1.12Tadd

［6］。将系数矩阵递推算法效率与相关文献的算法效率进行比较，其各系数矩阵递推算法时间复杂度见表1所示。

k次B样条基与文献［6］中的k＋1阶B样条基对应。从表1可看出，本算法的时间复杂度优于另外几种算法。

为验证本算法的高效性，将Deboor算法［2］、递推矩阵算法［6］与本算法均用C语言代码实现，然后在主频为2.99GHz的计算机运行比较。以计算5000次NURBS曲线上的点所需时间为基准，得出3种算法的平均时间开销分别为3.160 222、1.224 315、0.917 387ms。由此可见，本算法在效率上具有一定的优势，能为NURBS曲线的高速高精度插补提供有力保证。

表1 各系数矩阵递推算法时间复杂度Tab.1 Time complexity of different coefficient matrix recursion algorithms

4 NURBS矩阵表示在直接插补中的应用

近年来，随着NURBS曲线曲面被广泛应用于产品设计中，NURBS曲线的直接插补技术也越来越受到国内外学者的重视。2007年，王田苗等［9］将Deboor算法用于NURBS曲线的直接插补中，但由于Deboor算法在求值求导过程中存在大量重复递推计算，与NURBS矩阵表示算法相比，不能通过预处理减小插补周期内的计算量，难以保证插补的实时性。

4.1 NURBS曲线上点的计算

在NURBS曲线的直接插补中需要完成一维参数空间到三维坐标空间的映射，计算大量插补点的坐标，以得到下一个插补周期中刀具的进给增量。可先调用上面的算法进行预处理，求得k次B样条基的系数矩阵Mk（i），进而得到不同分段区间内NURBS曲线的矩阵表示式。对给定参数u，要计算其在三维坐标空间的映射点，只需判断u所处的分段区间并调用相应的系数矩阵，再将u的值代入式（7）即可求得NURBS曲线的坐标（Cx，Cy，Cz）。

4.2 NURBS曲线上各点处的导数及曲率计算

在NURBS曲线的直接插补中，为满足一定的加工精度和机床动力性能，常常需要根据曲线的曲率对刀具的速度、加速度等状态进行实时控制，这就需要计算曲线在某点处的导数。首先通过对式（7）进行变换［8］可得到：）

其中，Mk（u）、Q（u）、W（u）与参数u无关，简写为Mk、Q、W。再对式（16）两边求r阶导数：

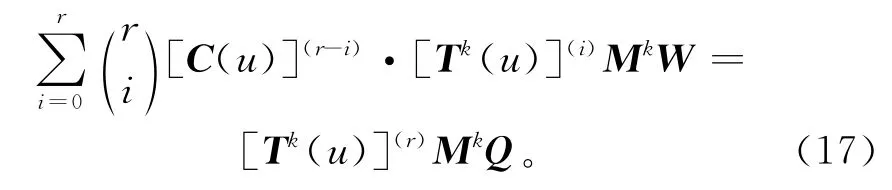
由式（17）可递推出曲线C（u）在某点处的r阶导数C（r）（u）。一般在NURBS曲线插补中只涉及曲线的一阶和二阶导数，其计算公式为：

在插补过程中，由于进给步长很小，可用圆弧近似各步长间的曲线，将该圆弧半径作为对应插补点的曲率半径。利用式（18）、（19）可计算曲率半径ρ，

此外，实时插补过程中还要不断通过计算进给步长确定下一时刻插补点的位置，通常采用的方法是一阶或二阶泰勒展开公式。式（20）同样需要反复采用曲线在插补点处的导数信息，可见，NURBS曲线求值求导算法的效率对保证其插补实时性具有非常重要的作用。

5 结束语

基于文献［5］的思想，将Deboor－Cox递推公式中的B样条基用幂函数表示，利用公式两边次数相同项的系数相等的关系，得出系数矩阵元素之间的递推关系。本研究对该关系式进行变量代换，避免了中间量的重复计算。再通过对该关系式进行形式变换、元素提取、组合叠加，最终得出系数矩阵的显式递推矩阵公式，进一步减小了计算量。与传统的Deboor算法相比，本算法采用矩阵表示NURBS曲线，便于对曲线进行预处理，避免了重复递推，更有利于保证插补的实时性。与其他矩阵递推算法相比，本算法的时间复杂度更优，且易于用代码实现。本算法不仅可用于任意阶NURBS曲线和B样条曲线的矩阵表示及其升阶、降阶，同时，还可为进一步研究NURBS曲面表示和直接插补奠定基础。

［1］施法中.计算机辅助几何设计与非均匀有理B样条［M］.北京：高等教育出版社，2001：211－310.

［2］Deboor C.A practical guide to splines［M］.New York：Springer－Verlag，1978：115－117.

［3］Choi B K，Yoo W S，Lee C S.Matrix representation for NURBS curves and surfaces［J］.Computer Aided Design，1990，22（4）：235－240.

［4］王学福，孙家广，秦开怀.NURBS的符号矩阵表示及其应用［J］.计算机学报，1993，16（1）：28－34.

［5］Grabowski H，Li X.Coefficient formula and matrix of nonuniform B－spline functions［J］.Computer Aided Design，1992，24（12）：637－642.

［6］秦开怀.NURBS曲线和曲面的递推矩阵及其应用［J］.计算机学报，1996，19（12）：941－947.

［7］潘日晶.NURBS曲线曲面的显式矩阵表示及其算法［J］.计算机学报，2001，24（4）：358－366.

［8］王国勋，舒启林，王军，等.NURBS直接插补技术中快速求值求导算法［J］.东北大学学报：自然科学版，2012，33（7）：1021－1024.

［9］王田苗，曹宇男，陈友东，等.基 于de Boor算 法 的NURBS曲线插补和自适应速度控制研究［J］.中国机械工程，2007，18（21）：2608－2613.