(2+1)维Kaup-Kupershmidt方程的精确行波解①
贾 荣,冯大河,程源泉,余晶晶
(桂林电子科技大学 数学与计算科学学院,广西 桂林 541004)
求解非线性偏微分方程(组)的精确解一直是数学物理领域的重要研究课题之一,非线性方程的波解描述了众多重要现象和动力学过程,因此被广泛应用于物理、工程技术和数学等领域,如非线性光学、量子论、流体力学、弹性理论和凝聚态物理等。到目前为止,众多有效的求解非线性偏微分方程(组)的方法已被提出,包括反散射方法[1]、Backlund变换法[2]、Darboux变换法[2]、Hirota双曲线性法[2]、齐次平衡法[3-5]、动力系统分支理论方法[6-8]、Tanh函数法[1]、Jacobi椭圆函数展开法[9]。其中,Tanh函数法是求解非线性偏微分方程精确解的一种有效方法。2003年,Fan Engui[10]提出了一种新的代数方法,即Fan子方程法,2007年,Feng Dahe等[11]改进了这种方法。与Tanh函数法相比,利用Fan子方程法求解方程易得更多一般的行波解。目前,不少学者利用该方法研究非线性偏微分方程的问题。Feng Dahe等[12]利用该方法求解ageneralized Hirota-Satsuma coupled KdV equation的精确行波解。元艳香等[13]获得Zhiber-Shabat方程更多丰富的精确解,Lu Hailing等[14]利用对称函数方法研究了(2+1)维Kaup-Kupershmidt(KK)方程的精确解,Hrawy等[15]利用指数函数法得到了(2+1)维KK方程新的精确解。为此,利用Fan子方程法研究(2+1)维Kaup-Kupershmidt方程,并给出该方程的精确解和相应的波形图。
1 利用Fan子方程法求解(2+1)维Kaup-Kupershmidt方程
利用Fan子方程法研究(2+1)维Kaup-Kupershmidt方程:
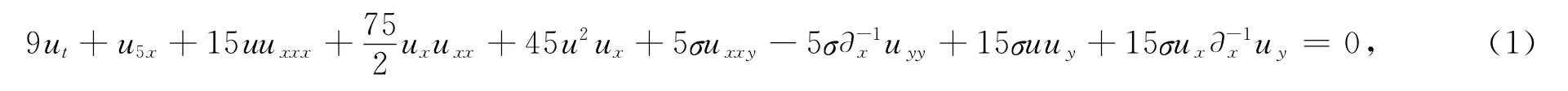


作行波变换u(x,y,t)=U(ξ),ξ=x+ky+et,其中,k、e为常数,方程组(3)转化为:

根据Fan子方程法,设方程组(4)的解为:

其中ai、bi为待定系数。新变量φ=φ(ξ)满足子方程:

其中ε=±1,cj(j=0,1,…,4)为待定常数。因此,对于变量ξ的微分则转化为新变量φ(ξ)的微分:
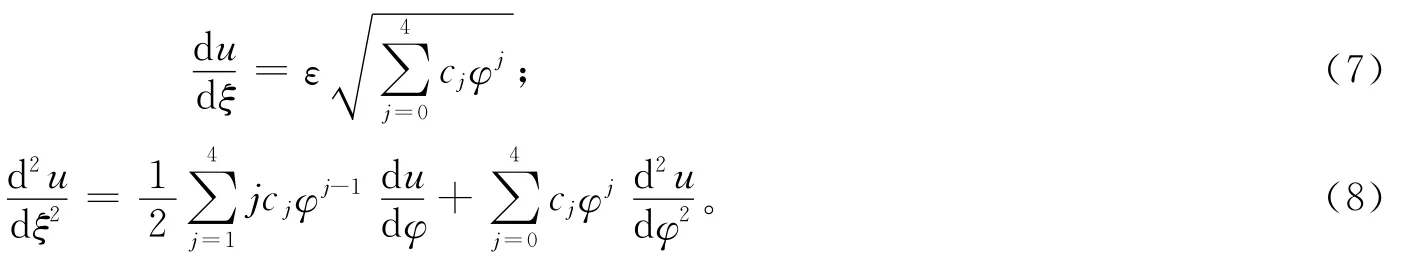
把式(5)~(8)代入方程组(4),然后平衡最高阶导数项和最高阶非线性项,可得n1=n2=2。方程组(4)的解可表示为:

令ε=1,φi和φi的系数为0,由此得到一系列关于ai、bi(i=0,1,2)的代数方程,应用符号计算软件Maple求解此方程,得到该方程组15种情况的解,从而得到方程组(3)的30组精确解。
2 (2+1)维Kaup-Kupershmidt方程的30组精确解
2.1 c0=0,c1=0,c2=0,c4=0的有理函数解
设a2=0,a1=-c3/4,a0=-kσ/3,b2=0,b1=-kc3/4,b0=k2/3-3e/5σ,其中σ2=1,c3≠0,k、e为任意常数,由c0=0,c1=0,c2=0,c4=0,可得方程(6)的1组有理函数解:

把方程(10)代入方程(9),方程组(3)的精确解为:
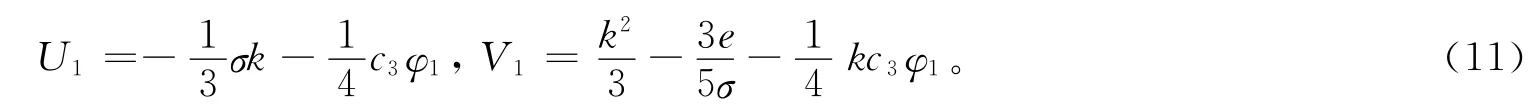
2.2 c2=0,c4=0,c3>0的Weierstrass椭圆函数解
设a2=0,a1=-c3/4,a0=-σk/3,b2=0,b1=-kc3/4,b0=(80σk2+3c1c3-144e)/240σ,其中σ2=1,c1≠0,c0、k、e为任意常数,由c2=0,c4=0,c3>0,可得方程(6)的1组Weierstrass椭圆函数解:

其中g2=-4c1/c3、g3=-4c0/c3为双周期Weierstrass椭圆函数的变量。把方程(12)代入方程(9),方程组(3)的精确解为:

2.3 c0=0,c1=0,c4=0的三角函数解和双曲函数解
设a2=0,a1=-c3/4,a0=-σk/3-c2/12,b2=0,b1=-kc3/4,b0=(80σk2-20σkc2-c22-144e)/240σ,其中σ2=1,c3≠0,k、e为任意常数,由c0=0,c1=0,c4=0,可得方程(6)的1组三角函数解、1组双曲函数解:
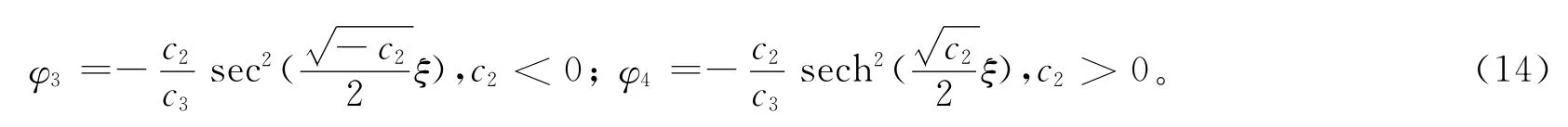
把方程(14)代入方程(9),方程组(3)的精确解为:
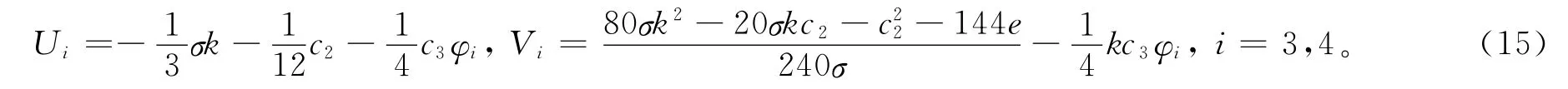
2.4 c0=0,c1=0,c2=0,c4=0的有理函数解
设a2=0,a1=-2c3,a0=-σk/3,b2=0,b1=-2kc3,b0=k2/3-3e/5σ,其中σ2=1,c3≠0,k、e为任意常数,由c0=0,c1=0,c2=0,c4=0,可得方程(6)的1组有理函数解:

把方程(16)代入方程(9),方程组(3)的精确解为:
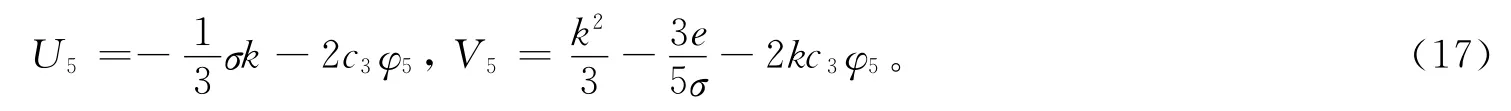
2.5 c2=0,c4=0,c3>0的Weierstrass椭圆函数解
设a2=0,a1=-2c3,a0=-σk/3,b2=0,b1=-2kc3,b0=(5σk2+33c1c3-9e)/15σ,其中σ2=1,c1≠0,c0、k、e为任意常数,由c2=0,c4=0,c3>0,可得方程(6)的1组Weierstrass椭圆函数解:

把方程(18)代入方程(9),方程组(3)的精确解为:

2.6 c0=0,c1=0,c4=0的三角函数解和双曲函数解
设a2=0,a1=-2c3,a0=-σk/3-2c2/3,b2=0,b1=-2kc3,b0=(5σk2-10σkc2-11-9e)/15σ,其中σ2=1,c3≠0,k、e为任意常数,由c0=0,c1=0,c4=0,可得方程(6)的1组三角函数解、1组双曲函数解:

把方程(20)代入方程(9),方程组(3)的精确解为:
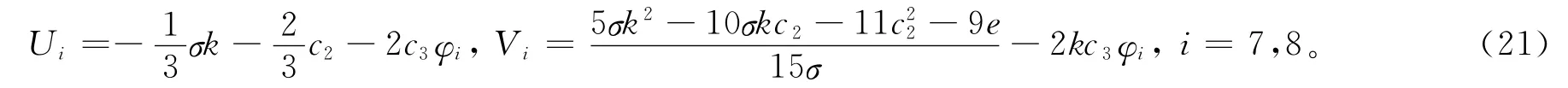
2.7 c0=0,c1=0,c2=0,c3=0,c4>0的有理函数解
设a2=-c4,a1=0,a0=-σk/3,b2=-kc4,b1=0,b0=k2/3-3e/5σ,其中σ2=1,k、e为任意常数,由c0=0,c1=0,c2=0,c3=0,c4>0,得到方程(6)的1组有理函数解:

把方程(22)代入方程(9),方程组(3)的精确解为:

2.8 c0=0,c1=0,c3=0的三角函数解和双曲函数解
设a2=-c4,a1=0,a0=-σk/3-c2/3,b2=-kc4,b1=0,b0=(5σk2-5σkc2--9e)/15σ,其中σ2=1,k、e为任意常数,由c0=0,c1=0,c3=0,可得方程(6)的1组三角函数解、1组双曲函数解:
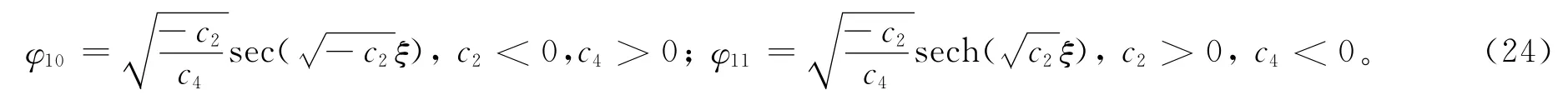
把方程(24)代入方程(9),方程组(3)的精确解为:
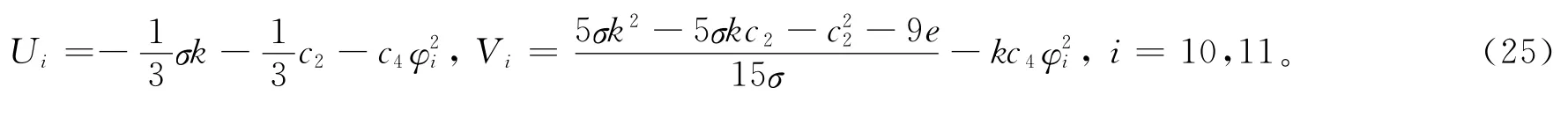
2.9 c1=0,c3=0的三角函数解、双曲函数解和3组双周期Jacobi椭圆函数解
设a2=-c4,a1=0,a0=σk/3-c2/3,b2=-kc4,b1=0,b0=(5σk2-c0c4-5σkc2--9e)/15σ,其中σ2=1,k、e为任意常数,由c1=0,c3=0,可得方程(6)的1组三角函数解、1组双曲函数解、3组双周期Jacobi椭圆函数解:

其中m(0<m<1)为Jacobi椭圆函数的模。把方程(26)~(30)代入方程(9),方程组(3)的精确解为:

2.10 c0=0,c1=0,c2=0的指数函数解和有理函数解
设a2=-c4,a1=-c3/2,a0=(3-16σkc4)/48c4,b2=-kc4,b1=-kc3/2,b0=(240+1280σk2,其中σ2=1,c3≠0,k、e为任意常数,由c0=0,c1=0,c2=0,可得方程(6)的1组指数函数解、1组有理函数解:
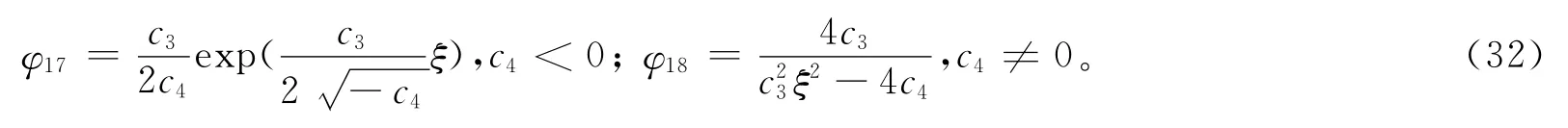
把方程(32)代入方程(9),方程组(3)的精确解为:

2.11 c0=0,c1=0的三角函数解和双曲函数解
设a2=-c4,a1=-c3/2,a0=,其中σ2=1,c3≠0,c4≠0,k、e为任意常数,由c0=0,c1=0,可得方程(6)的1组三角函数解、1组双曲函数解:
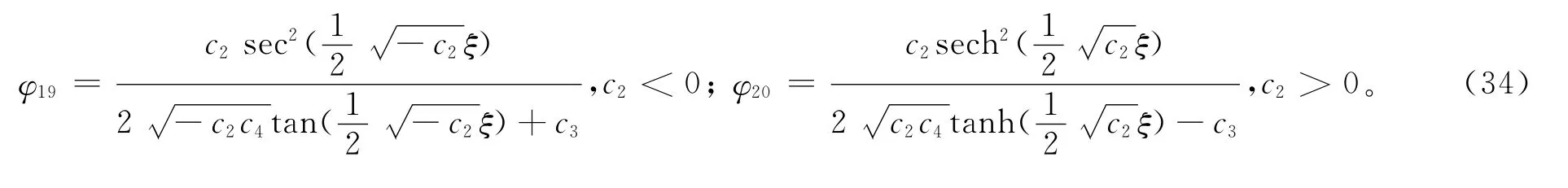
其中当c2=/4c4时。将方程(34)代入方程(9),方程组(3)的精确解为:

2.12 c0=0,c1=0,c2=c32/4c4的三角函数解和双曲函数解
设a2=-,其中σ2=1,c3≠0,k、e为任意常数,由c0=0,c1=0,c2=c32/4c4,可得方程(6)的1组三角函数解、1组双曲函数解:

把方程(36)代入方程(9),方程组(3)的精确解为:

2.13 c0=0,c1=0,c2=0,c3=0,c4>0的有理函数解
设a2=-8c4,a1=0,a0=-σk/3,b2=-8kc4,b1=0,b0=k2/3-3e/5σ,其中σ2=1,k、e为任意常数,由c0=0,c1=0,c2=0,c3=0,c4>0,可得方程(6)的1组有理函数解

把方程(38)代入方程(9),方程组(3)的精确解为:
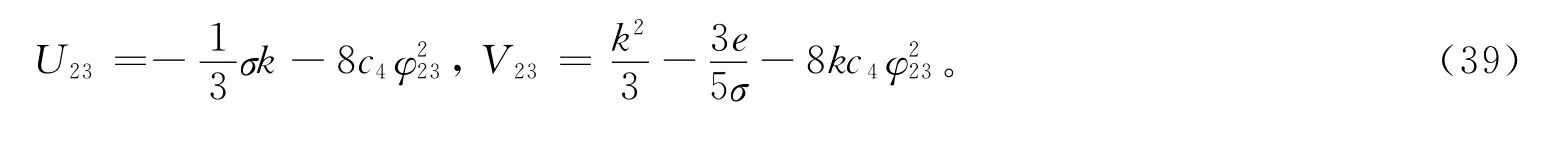
2.14 c0=0,c1=0,c3=0三角函数解和双曲函数解
设a2=-8c4,a1=0,a0=-σk/3-8c2/3,b2=-8kc4,b1=0,b0=(5σk2-40σkc2-176-9e)/15σ,其中σ2=1,k、e为任意常数,由c0=0,c1=0,c3=0,可得方程(6)的1组三角函数解、1组双曲函数解:

把方程(40)代入方程(9),方程组(3)的精确解为:
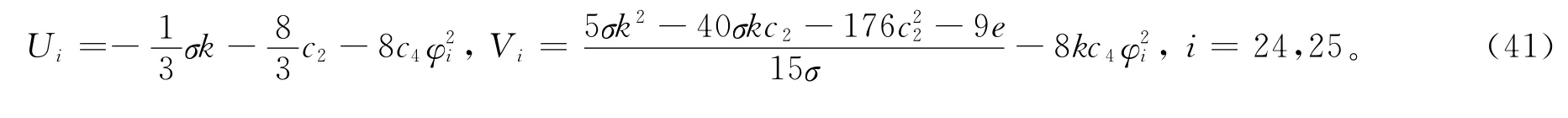
2.15 c1=0,c3=0的三角函数解、双曲函数解和3组双周期Jacobi椭圆函数解
设a2=-8c4,a1=0,a0=-σk/3-8c2/3,b2=-8kc4,b1=0,b0=9e)/15σ,其中σ2=1,k、e为任意常数,由c1=0,c3=0,可得方程(6)的1组三角函数解、1组双曲函数解、3组双周期Jacobi椭圆函数解:

把方程(42)代入方程(9),方程组(3)的精确解为:

3 (2+1)维KK方程相应的波形图
(2+1)维Kaup-Kupershmidt方程30组解的图形大致分为5类:
1)KK方程的第3、7、10、11、24、26组解有相似的图形,其中第3组解的波形如图1所示。

图1 当σ=1,c2=-0.04,k=e=1,t=0时U3、V3的波形Fig.1 The waveforms ofU3,V3 whenσ=1,c2=-0.04,k=e=1,t=0
2)KK方程的第4、8、12、13、25、27组解有相似的图形,其中第8组解的波形如图2所示。
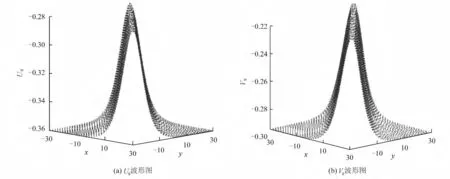
图2 当σ=1,c2=0.04,k=e=1,t=0时U8、V8的波形Fig.2 The waveforms ofU8,V8 whenσ=1,c2=0.04,k=e=1,t=0
3)KK方程的第14、15、16、28、29、30组解有相似的图形,其中第14组解的波形如图3所示。
4)KK方程的第18组解的波形如图4所示。

图3 当σ=1,c2=0.28,k=e=1,m=0.8,t=0时U14、V14的波形Fig.3 The waveforms ofU14,V14 whenσ=1,c2=0.28,k=e=1,m=0.8,t=0
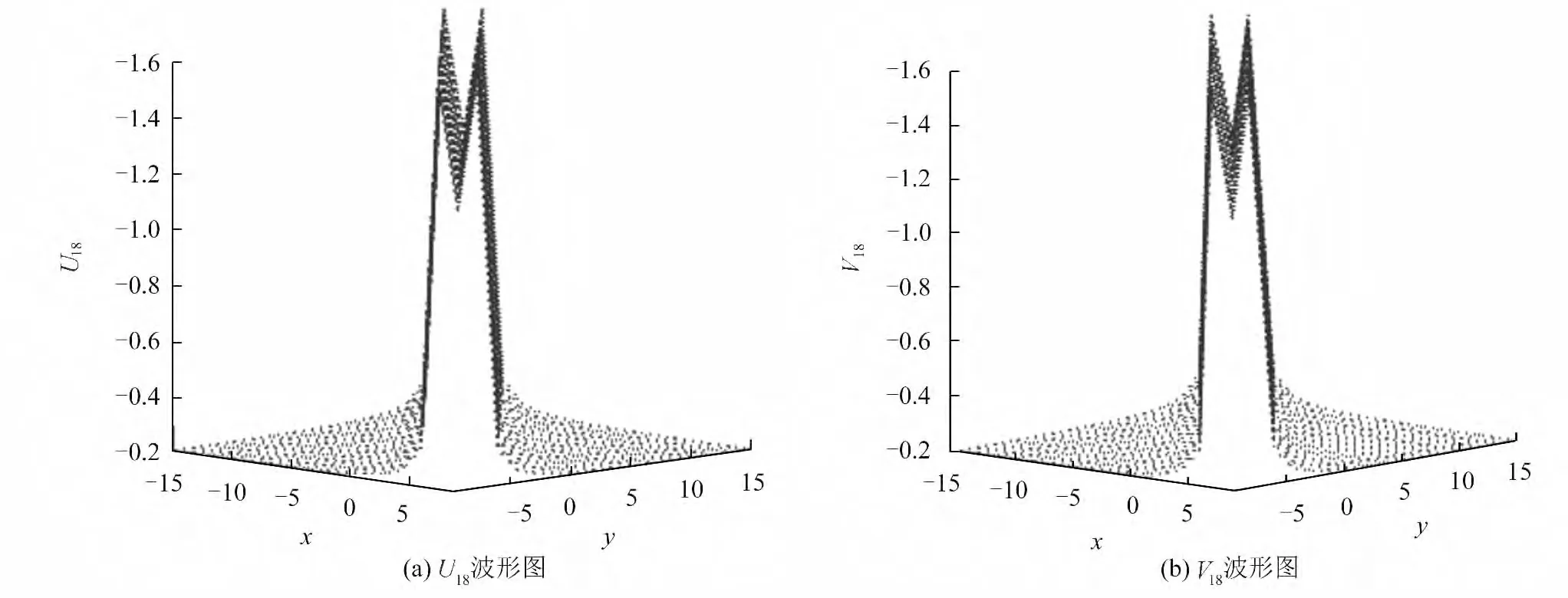
图4 当σ=1,c3=0.2,c4=0.02,k=e=1,t=0时U18、V18的波形Fig.4 The waveforms ofU18,V18 whenσ=1,c3=0.2,c4=0.02,k=e=1,t=0
5)KK方程的第20、22组解的波形如图5所示。
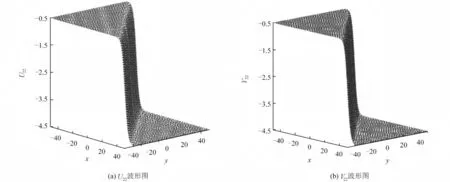
图5 当σ=1,c2=-0.01,c3=0.2,c4=1,k=e=1,t=0时U22、V22的波形Fig.5 The waveforms ofU22,V22 whenσ=1,c2=-0.01,c3=0.2,c4=1,k=e=1,t=0
4 结束语
利用Fan子方程法,借助符号计算软件Maple求解(2+1)维KK方程,获得了该方程的30组精确解。与其他求解(2+1)维KK方程方法相比,利用Fan子方程法得到的解更丰富、更具一般性。由此可见,Fan子方程法是求解非线性偏微分方程精确解的一种有效方法。后续研究可借助Fan子方程法或推广的Fan子方程法,解决非线性问题。
[1]郭玉翠.非线性偏微分方程引论[M].北京:清华大学出版社,2008:46-217.
[2]陈陆君,梁昌洪.孤立子理论及其应用[M].西安:西安电子科技大学出版社,1997:53-60.
[3]范恩贵,张鸿庆.非线性波动方程的孤波解[J].物理学报,1997,46(7):1254-1258.
[4]范恩贵,张鸿庆.非线性孤子方程的齐次平衡法[J].物理学报,1998,47(3):353-362.
[5]Wang Mingliang,Zhou Yubin,Li Zhibin.Application of homogeneous balance method to exact solutions of nonlinear equations in mathematical physics[J].Physics Letters A,1996,213:67-75.
[6]郭柏灵,刘正荣.CH-γ方程的两类新有界波[J].中国科学:A辑,2005,35(6):651-663.
[7]Liu Zhengrong,Ouyang Zhengyong.A note on solitary waves for modified forms of Camassa-Holm and degasperis-procesi equations[J].Physics Letters A,2007,366:377-381.
[8]刘正荣,杨喜艳.广义Camassa-Holm方程的显示孤子解[J].云南民族大学学报:自然科学版,2007,16(2):89-94.
[9]赵小山,徐伟.广义五阶KdV方程的新的周期波解与孤立波解[J].西南民族大学学报:自然科学版,2007,33(3):464-468.
[10]Fan Engui.Uniformly constructing a series of explicit exact solutions to nonlinear equations in mathematical physics[J].Chaos Solitons &Fractals,2003,16:819-839.
[11]Feng Dahe,Li Jibing,Lu Junliang,et al.The improved Fan sub equation method and its application to the Boussinseq wave equation[J].Applied Mathematics and Computation,2007,194:309-320.
[12]Feng Dahe,Li Kezan.Exact traveling wave solutions for a generalized Hirota-Satsuma coupled KdV equation by Fan subequation[J].Physics Letters A,2012,375:2201-2210.
[13]元艳香,冯大河,韩虎,等.Zhiber-Shabat方程的精确行波解[J].桂林电子科技大学学报,2012,32(2):162-166.
[14]Lu Hailing,Liu Xiqiang.Exact solutions to(2+1)-dimensional Kaup-Kupershmidt equation[J].Communications in Theoretical Physics,2009,52(5):795-800.
[15]Bhrawy A H,Biswas A,Javidi M,et al.New solutions to(1+1)-dimensional and(2+1)-dimensional Kaup-Kupershmidt equations[J].Results in Mathematics,2013,63(1/2):1422-6383.

