一种改进的二次误差测度简化算法①

张文新，温佩芝，黄 佳，朱立坤，邵其林

（桂林电子科技大学 计算机科学与工程学院，广西 桂林 541004）

在计算机图形学、三维动漫、反求工程等应用中，三维几何数字化模型通常用多边形网格表示［1］。由于三角网格模型数学表示简单，通用性和灵活性较好，得到了广泛的应用［2－3］。随着三维激光扫描技术的发展，所获得的三维数字化模型越来越精细、数据量越来越大，这些三维数字模型往往需要数百万的三角面片才能准确表达物体的细节特征。如果将这些模型通过互联网传输或在Web环境中展示，将是一个极具挑战性的难题，因而成为计算机应用及互联网领域的研究热点。在计算机处理速度和网络带宽有限的情况下，在Web中进行高分辨率的三维数字模型展示是不现实的，因此，对复杂度高的三维数字化模型进行简化是Web3D展示最关键的技术。网格模型简化的目的是将多边形网格模型用一个近似模型表示，同时要尽可能保留原始模型的特征，包括几何特征和视觉特征，但模型的数据量要远小于原始模型。近年来，国内外很多学者对网格模型简化做了大量研究，提出了一系列简化算法，如顶点删除算法［4］、网格重新划分算法［5］、边折叠算法［6］、区域合并算法［7］、小波变换算法［8］、包络网格算法［9］等。其中，边折叠作为最重要的简化算法之一，在几何数字化网格模型简化算法研究方面得到了广泛应用。

边折叠算法由Hoppe［6］在1993年首先提出，采用全局能量函数最优化方法简化模型，把距离能量、表示能量和弹簧能量引入全局优化方程中。实验证明，该方法简化生成的网格模型效果是所有简化算法中最好的［10］。但由于其优化过程是非线性的，计算复杂，很难满足实时绘制要求。为此，Garland等［11］提出一种基于二次误差测度（quadric error metric，简称QEM）的边折叠网格简化方法，该方法以新顶点到被折叠边的2个顶点关联平面的距离平方和作为误差度量，简化生成的网格模型质量较高，且计算简单、运行速度较快。刘晓利等［12］在QEM简化算法的基础上，引入顶点的尖特征度，并将其加入到误差测度中，保留了网格模型的特征信息，但由于只在二次误差测度中加入了一个惩罚项，且需要根据经验设定阈值和惩罚系数。李基拓等［13］提出一种利用质点－弹簧模型优化网格形状的边折叠算法，该方法需要作原始模型曲面和简化模型曲面双映射处理，操作比较繁琐。周元峰等［14］提出一种基于体积平方度量的三角形折叠网格简化方法，在极小化误差目标函数中引入几何形状因子和法向约束因子，取得了较好的简化效果。为此，在QEM简化算法的基础上，把顶点曲率和局部区域面积引入二次误差测度中，增大曲率变化较大区域的顶点误差代价，进而改变边折叠的顺序，使得简化网格模型的特征区域得以保留。

1 基于QEM算法的网格模型简化方法

1.1 边折叠操作的概念

对边（vi，vj）进行折叠操作是将顶点vi、vj移动到一个新顶点vn，且删除以（vi，vj）为边的三角形，其他邻接三角形需要进行相应的调整，如图1所示。

图1 边折叠操作Fig.1 The edge collapse operator

1.2 误差测度的计算

1997年Garland等［11］提出了三维网格模型的二次误差测度简化算法，以边折叠操作生成的新顶点到被折叠边的2个顶点关联平面的距离平方和作为误差测度度量，根据边折叠后的简化模型与原始模型之间的误差，即折叠代价Δv＝vTQv衡量和判断一条边能否被折叠简化。对于三维空间顶点v＝［vxvyvz1］T与其关联的三角形平面的集合P（v），误差代价Δv定义为：

其中p＝［abcd］T表示三维空间中的平面方程ax＋by＋cz＋d＝0，且a2＋b2＋c2＝1。式（1）可变换为：

其中Kp为一个4×4的对称矩阵，令顶点v的二次误差测度矩阵。对于边（vi，vj）→vn，折叠代价为Δvn＝vnT（Qi＋Qj）vn，用Qn＝Qi＋Qj表示新顶点vn的二次误差测度矩阵，可快速计算边折叠所造成的误差，同时更新相应的边折叠顺序。

新顶点的最佳位置可通过求式（2）的极小值确定，即∂Δv／∂x＝∂Δv／∂y＝∂Δv／∂z＝0，通过线性方程组求解顶点vn：

若方程组（4）有唯一解，则vn可由式（5）得到，

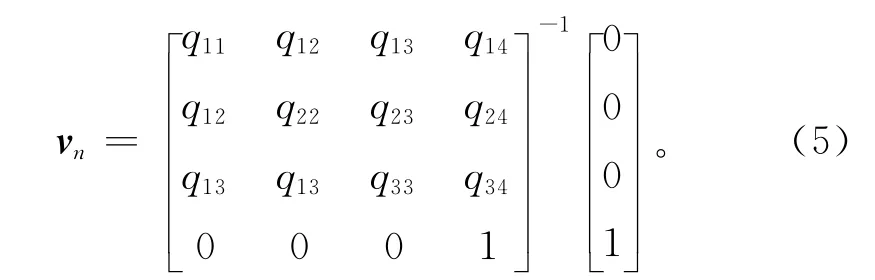
如果矩阵不可逆，QEM试图沿着边（vi，vj）找到一个最优的顶点。若找不到合适的顶点，则算法会在vi、vj和（vi，vj）／2中寻找一个合适的点。实验证明，QEM算法对三维网格模型的简化效果明显，且运行速度快，但该方法简化生成的网格是均匀的，特别是在低分辨率的情况下，简化生成的网格模型损失了原始模型的细节特征，引起细节部分的失真。为了能在简化网格模型中更好地保持原始模型的细节特征区域，提出一种改进的基于边折叠网格简化方法，根据网格模型在折痕、拐点等特征区域网格曲率较大、三角面片较小的特点，将顶点曲率和局部区域面积引入二次误差测度计算中，给出类似QEM算法的误差标准，并用该误差标准指导网格模型进行边折叠操作。

2 改进的QEM算法

边折叠包括2个重要的因素：1）确定边折叠的顺序；2）确定边折叠后新顶点的位置。这2个因素决定了边折叠简化后的网格模型质量。为了更好地指导边折叠的顺序，将顶点的曲率引入二次误差测度中，通过增大顶点曲率变化较大区域的误差测度值，改变边折叠的顺序，使得原始网格模型的细节特征在简化网格模型中得以保留。另外，为了使简化后的网格模型三角面片分布更加合理均匀，在重点特征区域用较多三角面片表示，在平坦区域用较少三角面片表示，引入了另一个误差约束量——局部区域面积。

2.1 顶点曲率的计算

由于三维几何数字化网格模型通常由一系列的三角面片组成，三角面片是二阶不可微的曲面，理论上不存在曲率的概念，但可看作光滑表面的分段近似，这里所说的曲率是指一个近似曲率［15］。研究表明，人的视觉对几何数字化网格模型的折痕、拐点等关键特征比较敏感，因此，在进行网格模型简化时应尽量保留这些部位。一般情况下，在三维几何数字化网格模型平坦区域，曲率较小；在三维几何数字化网格模型折痕、拐点等特征区域，曲率较大。若一个顶点的曲率越大，说明该顶点越能代表网格模型的细节特征。对于这些顶点推迟其边折叠的顺序，使得原始网格模型的主要特征信息得以保留。

对于任意一个三角网格t0，取其3个顶点分别为vi－1，vi，vi＋1，那么t0的单位法向量可用下式计算：

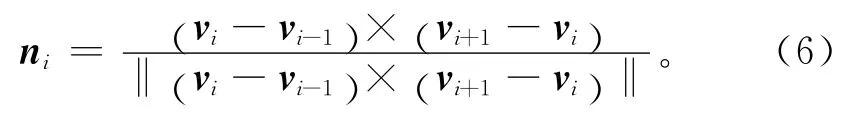
为了得到顶点vi的曲率，需计算顶点vi的法向量。顶点法向量可通过计算与该点关联的所有三角网格的法向量进行面积加权平均得到［16－17］，

其中：k为与顶点vi相关三角面片的个数；Si为第i个三角网格的面积。得到顶点的法向量后，可计算该顶点的曲率为

其中α（nvi，ni）为顶点法向量nvi与三角网格单位法向量ni的夹角。

得到三角网格模型中每个顶点的曲率，并把曲率加入误差测度中。若一个顶点的曲率越大，表示该顶点的位置越能表现模型的细节特征，将曲率大的边放入堆底，曲率小的边放入堆顶，根据折叠代价的大小进行边折叠操作。

2.2 局部区域面积加权

QEM算法简化后的网格模型三角面片分布比较均匀，不能很好地突显原始网格模型的重要特征。希望简化的网格模型在特征区域三角面片相对较多，在平坦区域三角面片相对较少，这样才能更好地表现原始模型的整体面貌。因此，为了在简化模型后有效保持原始模型的特征，并使三角面片分布更加合理，把局部区域面积引入折叠代价计算中，以改变边折叠的顺序，从而达到更好的简化效果。

如图2所示，顶点v的邻接三角形为t0，t1，t2，t3，t4，t5，所有邻接三角形的面积之和称为顶点v的局部区域面积SLR。网格模型中任一顶点的局部区域面积可表示为

其中：k为顶点v邻接三角形的个数；Si为第i个邻接三角形的面积。

图2 局部区域面积示意图Fig.2 The schematic diagram of local region area

在计算边折叠代价时，把顶点曲率和局部区域面积添加到式（2）中，将式（2）得到的代价乘以顶点的曲率，然后除以该顶点的邻接局部区域面积，把得到的新代价作为边折叠最后代价：

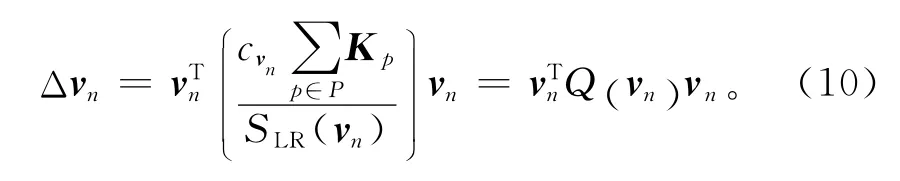
对于新顶点位置的确定，QEM算法中通过求式（2）的极小值确定，其求解过程不但复杂而且几何意义不明确。对此，采用半边折叠操作，根据一条边的2个顶点的折叠代价大小确定保留哪一个顶点。由于半边收缩操作未引入新的顶点，无需增加额外的存储开销，从而可提高简化速度。

2.3 算法描述

首先采用堆排序的方式对边序列按照折叠误差的大小进行排序，并存储在待折叠边的误差队列中，然后每次从堆中取出误差最小的边进行简化操作。算法步骤为：

1）读入原始网格模型，计算每个网格模型顶点的二次误差矩阵Q；

2）计算三角网格模型中每个顶点的曲率cvn，结合顶点相邻三角网格的局部区域面积SLR（vn），计算网格中顶点的二次误差测度矩阵Q（vn）＝

3）计算每条边的折叠代价Δvn，依据折叠代价的大小将所有的边排序后放入堆中，折叠代价最小的置于堆顶，折叠代价最大的置于堆底；

4）从堆中取出折叠代价最小的边进行折叠操作，同时删除该边及与该边关联的三角网格，并更新所有相关几何元素的状态；

5）重复上述过程直到达到简化要求，否则转步骤4）。

3 实验结果分析

为了证明本算法的性能，在Microsoft Visual C＋＋、2.94GHz Intel（R）2、2GB内存PC机上实现该算法，采用OPENGL图形库渲染模型，然后将本算法与QEM算法的简化效果进行对比，实例为小鹿模型和人脸模型。图3（a）为小鹿的原始网格模型，包含10 648个三角面片；图3（b）为人脸原始模型，包含13 472个三角面片。图4为利用QEM算法和本算法对小鹿模型进行简化得到的模型，简化模型剩余三角面片分别为2000个、800个、300个。

从图4（a）～（c）可看出，利用QEM算法得到的简化模型网格分布均匀，在平坦区域也占用较多的网格，既造成了网络浪费，也未能很好突出模型的特征。经大规模简化后，QEM算法简化的模型鹿角和嘴部开始出现模糊现象，图4（c）简化到只剩300个三角面片时，造成了视觉上的退化。与QEM算法相比，本算法能在一定程度上保持模型重要特征，并使得简化后的模型网格分布比较合理，用较多的三角面片表示曲率变化较大区域，而在平坦区域用较少三角面片表示，如图4（d）中在鹿角、鹿嘴、鹿鼻等特征区域保留了较多的三角面片。这样，本算法在低分辨率的情况下，仍能保留简化后模型的几何特征，图4（f）比图4（c）更能突显鹿角和鹿嘴的细节特征。

图3 小鹿和人脸原始模型Fig.3 The original models of deer and face

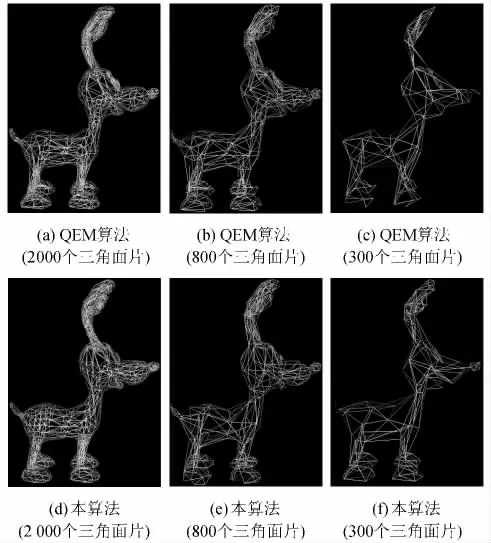
图4 小鹿的简化模型Fig.4 The simplified models of deer

图5为利用QEM算法和本算法对人脸模型进行简化得到的简化模型，剩余三角面片分别为3000个、1000个、500个。从这3组对比图可看出，利用本算法得到的人脸简化模型在眼睛、鼻子和嘴巴等特征区域网格分布较为稠密，有效地保持了较多的细节特征，在视觉效果上更接近原始模型。

图5 人脸模型的简化阴影图比较Fig.5 The simplified models of face

4 结束语

针对大数据量的三维网格几何模型在Web3D展示中的难点，提出了一种改进的二次误差测度简化算法，将顶点曲率和局部区域面积引入网格简化误差代价计算中。实验表明，本算法在保留原算法运行速度快、效率高的同时，很好地保留了原始网格模型的细节特征，改善了三维几何数字化模型简化后在网络展示中的细节模糊的状况。由于数字化模型除了几何信息外，还具有纹理、颜色等属性，下一步将研究带属性的三角网格模型简化的问题，进一步提升三维数字化模型Web3D的展示效果。

［1］潘志庚，庞明勇.几何网格简化研究与进展［J］.江苏大学学报，2005，26（1）：67－71.

［2］Dong Wenlong，Li Jiankun，JayKuo C C.Fast mesh simplification for progressive transmission［C］／／Multimedia and Expo，2000IEEE International Conference on.New York：IEEE Computer Society Press，2000：1731－1734.

［3］卢威，曾定浩，潘金贵.支持外观属性保持的三维网格模型简化［J］.软件学报，2009，20（3）：713－723.

［4］William J S，Jonathan A Z，William E L.Decimation of triangle meshes［J］.Computer Graphics，1992，26（2）：65－70

［5］Turk G.Retiling polygonal surfaces［J］.Computer Graphics，1992，26（2）：55－64.

［6］Hoppe H.Progressive meshes［C］／／ACM Computer Graphics Procedings，Annual Conference Series，1996：99－108.

［7］Kalvin A D，Taylor R H.Superfaces：polygonal mesh simplication with bounded error［J］.IEEE Computer Graphics and Application，1996，16（3）：64－77.

［8］Lounsbery M，deRose T.Multiresolution analysis for surface of arbitrary topological type［R］.Washington：U－niversity of Washington，1994：47－64.

［9］张明敏，周昆，潘志庚.基于超包络网络的三角形网格简化算法［J］.软件学报，1999，10（6）：405－408.

［10］Cignoni P，Puppo E，Scopogno R.Representation and visualization of terrain surfaces at variable resolution［J］.The Visual Computer，1997，13：199－217.

［11］Garland M，Heckbert P S.Surface simplification using quadric error metrics［J］.Computer Graphics，1997，31（3）：209－216.

［12］刘晓利，刘则毅，高鹏东，等.基于尖特征度的边折叠简化算法［J］.软件学报，2005，16（5）：669－675.

［13］李基拓，陆国栋.基于边折叠和质点弹簧模型的网格简化优化算法［J］.计算机辅助设计与图形学学报，2006，18（3）：426－432.

［14］周元峰，张彩明，贺平.体积平方度量下的特征保持网格简化方法［J］.计算机学报，2009，32（2）：203－212.

［15］张果，刘旭敏，关永.一种基于近似曲率的边折叠简化算法［J］.计算机应用，2009，29（3）：729－731.

［16］Biermann H，Levin A，Zorin D.Piecewise smooth subdivision surfaces with normal control［C］／／Proceedings of SIGGRAPH 2000.Boston：Addison Wesley Professional，2000：113－120.

［17］Page D L，Koschan A，Sun Y，et al.Robust crease detection and curvature estimation of piecewise smooth surfaces from triangle mesh approximations using normal voting［C］／／Proceedings of the International Conference on Computer Vision and Pattern Recognition.San Francisco：Morgan Kaufmann，2001：162－167.