基于改进型混洗蛙跳算法的网格DAG任务调度①

戴 扶，黄文明，邓珍荣

（桂林电子科技大学 计算机科学与工程学院，广西 桂林 541004）

网格［1］将互联网上的各种资源集中在一个统一的框架内，为上层应用提供高效的资源服务。网格环境中的调度问题研究由来已久，调度问题可看作一个组合问题，将N个任务分配到M个资源上。这种优化组合问题非常适合用群体启发式算法来解决。目前，研究较多的是遗传算法（GA）、粒子群算法（PSO）、蚁群算法（ACA）、人工鱼群算法（AFSA）等［2－5］。混洗蛙跳算法（shuffled frog leaping algorithm，简称SFLA）是2003年由Eusuff等［6］提出的一种启发式算法，用于优化组合问题。此算法具有易理解、参数少、速度快、寻优能力强、实现简单等优点，已被广泛应用于水利管网、电力网络［7］中。具有依赖关系的任务可被抽象为一个有向无环图（directed acyclic graph，简称DAG）模型，DAG任务自身的结构和实际应用程序内的结构特征非常相似，因此，研究DAG任务调度问题更具有现实意义，但也使得任务调度问题更加复杂。

针对DAG任务的编码方式可分为2类：

1）间接编码方式。将资源先随机分配给任务，再利用其他手段剔除不符合DAG任务约束条件的解。如文献［8］中，任务的执行序不变，随机分配一个资源，然后通过计算节点的最长前驱路径和最短后继路径判断任务之间的关联度，剔除不符合约束条件的问题解。

2）直接利用DAG任务的约束条件进行编码。陈晶等［9］将DAG任务的高度值作为执行的优先级别，再根据级别随机分配优先权值，这些权值组合起来就是任务解的编码。

但这些方式都存在解码方式比较复杂或未考虑网格的动态性的缺陷。如果网络资源在编码阶段离开了网络环境，那么就会造成最后的分配方案失效。鉴于此，提出一种改进型混洗蛙跳算法解决网格DAG任务调度问题：将编码阶段和资源分配阶段分开，先依照DAG的依赖条件进行编码，再在任务派发阶段分配资源计算适应值；重新定义解空间度量规则，精简算法空间，减少算法的计算量；改进SFLA算法的搜索策略，使得解集能够迅速向最优解聚拢。

1 编码及适应函数

1.1 编码

问题解的组合方式能够反映出一个解的解决问题的效率。这种思想来源于管理领域内的岗位轮换制度，通过比较人员在不同岗位上的工作状况，进行统计分析，帮助优化整个组织的人力资源配置。同样地，DAG任务可看作一个组织机构，各个节点就是“轮岗人员”。一个完整的“人员职位安排”就是DAG任务调度问题的一个解，如图1所示。

图1 DAG任务编码示例Fig.1 Example of DAG task coding

受文献［10］分代（GS）算法的启发，将DAG任务按照高度值分配优先级，同一层的节点可视为元任务，执行序可任意排列；不同层的节点，优先级高的先执行。其实质就是将解的执行序列按约束条件分段，段内编号是确定的，但段内编号顺序是随意的。

1.2 适应度函数

适应值反映了解的优秀程度，在本研究中体现为总任务的执行时间。执行时间与资源分配方案息息相关，良好的分配方案可有效地提高解的质量，提升算法的搜索性能和收敛速度。采用动态最早完成优先（DEFF）算法［11］的思想对问题解进行资源分配，以保证每个节点的开始时间最早、执行时间最短。

设系统有m个资源，P＝｛P1，P2，…，Pm｝，DAG任务分为n个节点，T＝｛T1，T2，…，Tn｝，fat（Pi）为某个资源的可利用时间，Eij为资源Pi、Pj间的通信开销执行时间，p（Ti）为Ti的前驱节点集合，则Ti在Pj上的最早启动时间为：

fet，Ti（Pj）为任务Ti在Pj上的执行时间，则任务Ti在Pj上的完成时间为

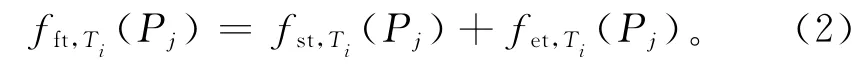
因此，任务Ti的最早结束时间F（Ti）和最早开始时间S（Ti）满足：

最终适应度函数为

1.3 解空间的度量

由于编码方式改变，需重新定义解空间的度量方式。受DAG任务约束条件的约束，高度值相同的节点只能在同一层中移动，可视这些节点在某个范围内是封闭的。因此，将DAG的层次视为解空间的维度，某个层次中的不同排序视为分布在这条基轴上的离散点，如图2所示。如此定义可有效地反映DAG的特点，并简化计算量。

图2 基轴示意图Fig.2 Example of basic shaft

定义1 基轴度量规则。在某个基轴上2个不同编码的α和β，α的编码通过K次交换可转换成β，则称α到β的距离为K，用K＝β－α表示。交换规则如下：

1）假设i为α中的第i个编码，若该元素与β中的第i个编码相同，则比较第i＋1个元素，直到比较α中所有元素；若不同，则跳到2）。

2）查找该编码在β中所处的位置j，然后将α中该编码所处位置和j位置的元素交换，再回到1）。

对于解空间中的任意解V，设其DAG模型分为U层，则解为U个基构成的向量。

定义2 解之间的欧式距离。对于解空间内任意2个解向量V1、V2，设解分为U层，ci为V2中第i个基到V1中第i个基的距离，则V2到V1的距离为：

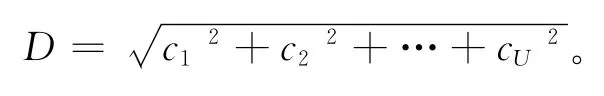
2 网格任务调度模型

用户将应用程序提交到任务池内，网格资源向网格资源管理器进行登记注册。调度器从任务池内顺序取出调度任务，同时从算法库中选择调度算法，利用资源管理器的资源列表和工具库内的一些必要工具，进行调度决策。调度决策完毕后，按照决策结果将任务发送到相应的网格资源，模型如图3所示。

图3 网格任务调度模型Fig.3 Grid task scheduling model

考虑资源间的通信开销，每个资源都有一份通信表，记录与相邻资源间的通信时间。调度方式采用非抢占式调度方式。

3 改进型混洗蛙跳算法（ISFLA）

3.1 SFLA

SFLA是为解决全局最优解而提出的一种变异模因进化算法［12］，它并不强调个体，而是强调个体所持有的思想变化［6］。通过向优秀个体学习，从而改进自己的思想，进而推动整个种群的进化。算法过程如下：

1）随机产生N只青蛙作为初始种群，然后计算每只青蛙的适应值，并按照适应值的优劣排序。2）根据式（5）将N只青蛙划分成M个模因族群。

其中：Yk为第k个模因族群；D（j）k为第k个族群中的第j只青蛙；j∈［1，N］，k∈［1，M］。

3）局部搜索。记录种群最优解Dg、族群内部的最优解Db和最差解Dw，根据式（6）进行进化。Dw先向Db进化，若进化失败，则向Dg进化，若仍失败，则Dw随机变化一下替换原来的Dw。

其中：rand（）为随机函数，取值（0，1）；dmax为允许移动的最大步长；Dx为Db或Dg。

4）全局搜索。将所有族群打散并重新按照适应度升序排序，若达到算法结束条件，则转到5），否则回到2）。

5）输出最优级。

3.2 改进策略

SFLA作为一种群体启发式算法虽然有参数少、全局寻优能力强的特点，但也存在容易陷入局部最优和收敛速度慢的缺点。在局部搜索策略中，Dw向Db和Dg学习为种群提供进化动力，并通过自我突变增加种群多样性，进化点单一、动力不足导致种群长期徘徊在旧的状态中。为此，将Db也作为进化点，向Dg学习，增加种群的进化动力，同时加入邻域搜索作为扩展搜索解空间的手段，增加种群多样性。

3.2.1 邻域搜索

设置一个邻域半径l，当解空间中一个解向目标解逼近时，若两解间的距离小于l，则开始探索周边空间的优秀解。

在算法的初期阶段，l的取值应大一些，使种群在初期能够尽可能地在整个解空间中移动，收集更多潜在的优秀解；在算法的后期，l值应该减小，使算法有较强的局部挖掘能力。因此，l的取值为

其中：i＝1，2，…，np；np为种群迭代次数。实验结果表明，Dmax＝9，Dmin＝1较为合适。

3.2.2Db向Dg进化策略

计算种群最优解的适应值A（Dg）、族群最优解的适应值A（Db）、族群最差解的适应值A（Dw）以及Dg与Db之间的距离D。若A（Db）＜A（Dg），直接用Db替换Dg；若A（Db）＜A（Dg），D＞l，按式（8）进化。

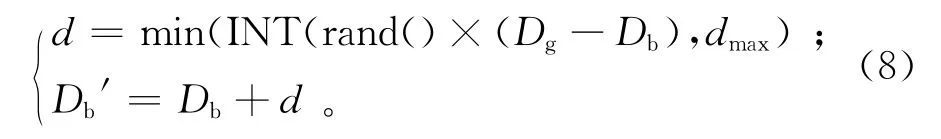
当A（Db′）＜A（Dg）时，用Db′替换Dg；A（Db′）＜A（Db）时，Db′替换Db；否则视为进化失败，进行邻域搜索。若A（Db）＝A（Dg）‖D＜l‖Db向Dg进化失败，也进行邻域搜索。由于邻域搜索可能对Db所持有的信息造成较大的破坏，设定一个突变因子τ，τ∈（0，1）。随机抽取U×τ个基，U为DAG任务的层数，根据式（9）进化。

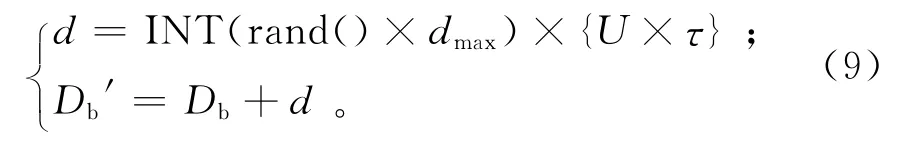
这样既能保持解的部分优良信息，又能对Db周围的空间进行探索。

当A（Db′）＜A（Dg）时，Db′替换Dg；A（Db′）≤A（Db）时，Db′替换Db；否则视为搜索失败。

3.2.3Dw向Db进化策略

若A（Dw）＞A（Db），则根据式（10）进化。

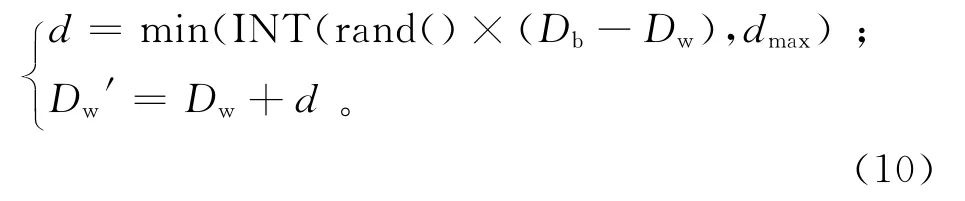
当A（Dw′）＜A（Db）时，Dw′替换Db；A（Dw′）＜A（Dw）时，Dw′替换Dw；否则视为进化失败，进行邻域搜索。

若A（Dw）＝A（Db）‖Dw向Db进化失败，进行邻域搜索，根据式（9）进行突变，Db换成Dw。

当A（Dw′）＜A（Db）时，Dw′替换Db，否则Dw′替换Dw，增加种群多样性。

4 系数确定和仿真及实验分析

为验证ISFLA的有效性，根据图3所示的网格任务调度模型，在Windows环境下用Java开发了一个网格环境任务调度仿真平台。在此平台上，分别对GA、PSO、SFLA和ISFLA的搜索性能及收敛速度进行实验。实验数据通过Matlab进行比较分析。

GA采用标准遗传算法，以轮盘赌法作为选择策略，单点交叉，一点变异，突变因子为0.05，交叉系数为0.6；PSO采用标准粒子群算法，惯性系数为0.8，c1、c2为学习因子，均取值2，进化步长在［1，8］；SFLA最大进化步长为3。

4.1 确定ISFLA的最大进化步长和突变因子

最大进化步长dmax如果设置较大，青蛙有可能越过最优值，而设置过小，移动速度会变慢，导致搜索效率太低。而设置突变因子τ的目的是为了在邻域搜索时，只让部分解的基进行突变，使得解的部分优秀信息有可能保存下来，同时也使得进化路径更加复杂，增加了计算负担，因此有必要对其进行讨论。

实验中，可用网格资源数量为4，任务量为50个节点的DAG任务，初始种群为200，族群数为10，族群循环次数10次，种群循环300次，测试步长时，τ＝0.25；测突变因子时，dmax＝3，结束条件为种群循环200次。每种步长各运行10次，然后求均值。结果如图4和表1、2所示。

从表1可看出，dmax＝9、7、3时，算法的时间开销都集中在45s左右，但当dmax＝2时，算法的时间开销提高到了67.10s，显然进化步长缩短导致解的进化速度放慢。表2为突变因子对跨度和算法时间开销的影响。从表2可看出，τ值的变化对算法的时间开销和调度跨度影响很小。从图4（a）可看出，dmax为7、9，算法的搜索性能明显差于dmax为2、3，这是由于进化步长过大导致解在进化时错失了许多潜在的优秀解。从图4（b）可看出，τ＝0.25时，算法的收敛速度比其他值要好些；τ＝0.80时，解的大部分基都参与了突变计算，使解本身的一些优良基因丢失，图4（b）中表现为收敛速度最差；τ＝0.10时，解中只有很少的基参与了突变计算，虽然保留了自身的优秀基因，但对自身的改良较少。因此，dmax＝3，τ＝0.25时，ISFLA的效果较好。

图4 ISFLA算法参数与调度跨度的关系Fig.4 The relation between SFLA parameters and span

表1 最大进化步长与调度跨度的关系Tab.1 The relation between max step size and span

表2 突变因子与调度跨度和ISFLA时间开销的关系Tab.2 The mutation factor，span and ISFLA time cost

4.2 验证算法的搜索性能和收敛速度试验

选取网格资源数量为4，任务量为30、50个节点的DAG任务。初始种群为200，族群数为10，族群循环次数10次，种群循环200次，结束条件为种群循环200次。GA、PSO、SFLA和ISFLA各 运 行10组，求每一代的均值。实验结果如图5所示。从图5（a）可看出，任务数为30时，在200次迭代过程中，各算法都能收敛到最优解附近，GA和ISFLA搜索性能稍好。当任务规模增加到50，ISFLA和GA的搜索性能明显好于SFLA和PSO，如图5（b）所示。这是由于ISFLA在进化策略中增加了邻域搜索策略，扩大了算法的探索空间，保证了种群的多样性，从而有效避免了局部收敛。从图5（c）可看出，PSO、GA分别经150、40次迭代才收敛到最优解附近，而SFLA、ISFLA分别在24、15次迭代就收敛到了最优解附近，收敛速度较快。可计算出ISFLA的收敛速度较GA、PSO、SFLA分 别 提 高了75%、94%和27%。从图5（d）可看出，ISFLA的收敛速度明显高于GA。因此，在有时间条件约束的情况下，ISFLA能更快找到全局最优解。

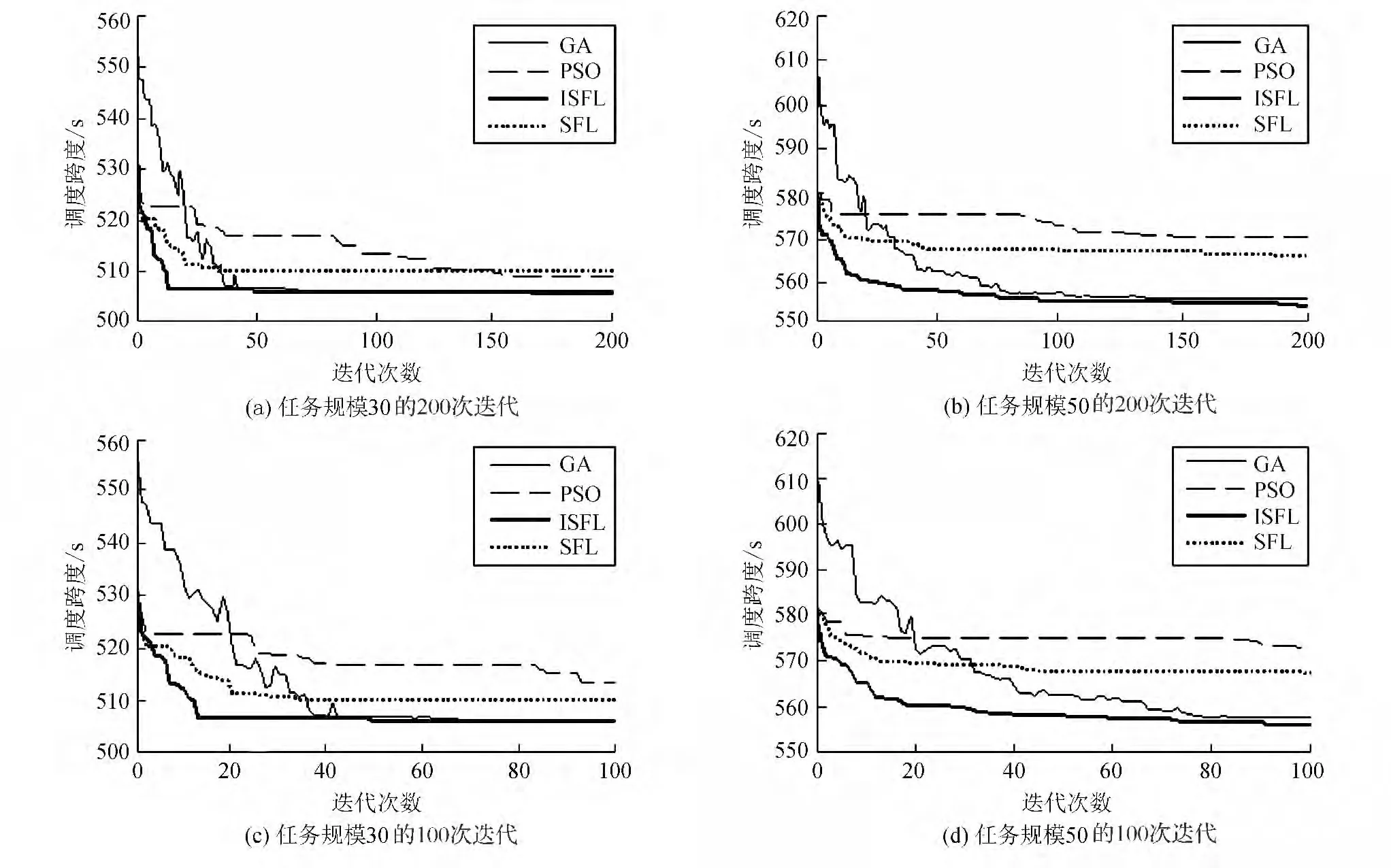
图5 2种任务规模下GA、PSO、SFLA和ISFLA的调度跨度Fig.5 The span of GA，PSO，SFLA and ISFLA under two scales

4.3 验证算法时间开销实验

实验设计：选用网格资源数量为4，任务量为10、20、30、40、50个节点的DAG任务。初始种群为200，族群数为10，族群循环次数10次，种群循环500次，结束条件为种群循环500次。4种算法各运行10组，分别对算法的时间开销求均值并进行比较。实验结果如表3所示。

表3 不同规模下算法时间跨度Tab.3 The solutions obtained by different algorithms under the different task scales s

图6为不同规模下4种算法的时间开销。从图6可看出，SFLA和ISFLA的时间开销比GA和PSO要小。而从表3中反映的数据来看，GA和ISFLA的结果更好。因此，在网格资源有限的情况下，ISFLA能够在较少的时间内给出最好的全局最优解。

图6 不同规模下4种算法的时间开销Fig.6 The time cost of four algorithms under the different task scales

5 结束语

通过综合分析网格动态环境中的DAG任务调度的特点，建立了一个网格任务调度模型。结合DAG任务和启发式群体智能算法的特点，设计了任务的编码方式和度量方式。基于邻域搜索策略和增加族群进化点，改进了SFLA的局部搜索策略，进而提出一种改进型混洗蛙跳算法。实验表明，该算法能够有效地提高搜索性能和收敛速度。下一步计划在多目标网格环境下的DAG任务调度算法中，把网格资源负载性能指标融入到优化策略。

［1］Foster I，Kesselman C，Tuecke S.The anatomy of the grid：enabling scalable virtual organizations［J］.International Journal of High Performance Computing Applications，2001，15（3）：200－222.

［2］兰舟.分布式系统中的调度算法研究［D］.成都：电子科技大学，2009：17－54.

［3］胡成玉.面向动态环境的粒子群算法研究［D］.武汉：华中科技大学，2010：19－67.

［4］冯春时.群智能优化算法及其应用［D］.合肥：中国科学技术大学，2009：23－55.

［5］刘波.蚁群算法改进及应用研究［D］.秦皇岛：燕山大学，2010：12－45.

［6］Eusuff M M，Lansey K E.Optimization of water distribution network design using the shuffled frog leaping algorithm［J］.Journal of Water Resources Planning and Management，2003，129（3）：210－225.

［7］Niknam T，Azad Farsani E.A hybrid self－adaptive particle swarm optimization and modified shuffled frog leaping algorithm for distribution feeder reconfiguration［J］.Engineering Applications of Artificial Intelligence，2010，23（8）：1340－1349.

［8］朱海，王宇平.融合安全的网格依赖任务调度双目标优化模型及算法［J］.软件学报，2011，22（11）：2729－2748.

［9］陈晶，潘全科.同构计算环境中DAG任务图的调度算法［J］.计算机工程与设计，2009，（3）：668－670.

［10］Carter B R，Watson D W，Freund R F，et al.Generational scheduling for dynamic task management in heterogeneous computing systems［J］.Information Sciences，1998，106（3）：219－236.

［11］马丹.任务间相互依赖的并行作业调度算法研究［D］.武汉：华中科技大学，2007：65－69.

［12］Eusuff M，Lansey K，Pasha F.Shuffled frog－leaping algorithm：a memetic meta－heuristic for discrete optimization［J］.Engineering Optimization，2006，38（2）：129－154.