改进的自适应免疫遗传算法在图像增强中的应用
刘 翔,董 昱
(兰州交通大学 自动化与电气工程学院,甘肃 兰州730070)
0 引 言
图像在采集、传输、接收等过程中由于受环境条件限制会使图像质量下降、视觉效果变差。为改善图像视觉效果或强调图像“有用信息”,需要对图像进行预处理,该过程就是图像增强[1]。图像增强效果的好坏直接决定了后续图像分析工作的工作量,因此,如何有效提高图像增强效果是图像处理中一个重要研究课题。
根据处理过程所在域不同,图像增强方法可分频域法、空域法两大类。频域法以修改图像的傅里叶变换为基础,属间接增强方法,通常这种方法的计算量较大且变换参数的选取人工干预较多。空域法以对图像像素直接处理为基础,属直接增强方法,其中非线性灰度变换因其图像对比度强、图像动态范围宽等优点成为图像增强的常用方法[2,3],而该方法的关键在于如何确定变换曲线的最佳参数。传统非线性变换法中的参数确定多采用人工试凑的方式,显然这种方式增强效果较差且不具自适应性。
本文提出了一种自适应免疫遗传算法用于确定非线性变换的最佳参数,实验表明:该算法可根据图像灰度性质自适应调节变换参数且得到的增强图像动态范围宽、对比度强、细节丰富。
1 改进的遗传算法
遗传算法是一种自适应启发式群体型概率性迭代式的全局收敛搜索算法,其基本思想源于生物进化论和群体遗传学,体现了优胜劣汰、适者生存的进化原则[4]。
通过对基本遗传算法的深入研究发现该算法主要存在三个缺陷:一是遗传算子的迭代搜索是随机的、盲目的,这往往会造成种群个体在进化的过程中出现退化现象;二是算法中各遗传算子和免疫算子的概率在整个进化过程中恒定不变,从而影响了算法的自适应性和收敛速度;三是交叉、变异操作时所针对的基因位置和位数是固定的,这使得种群个体多样性不易维持。为了解决上述问题,本文对三大缺陷逐一作了改进,提出了一种新型的自适应免疫遗传算法。
针对缺陷一,本文借鉴免疫算法的选择性和目的性,将免疫算子引入,与遗传算子相结合构成主要的遗传操作。针对缺陷二,该算法根据种群个体的适应度动态调整遗传算子的概率:在群体收敛至局部极值附近时,增大变异概率,从而增加种群多样性,跳出局部最优解;而当群体在解空间分散时,则增大交叉概率,加快收敛速度,这样既保证了向全局最优解逼近,又保证了一定的收敛速度[5]。针对缺陷三,该算法中变异操作采用多位变异策略,且根据个体适应度动态调整变异位数:适应度高的个体变异位数少,甚至无变异位;适应度低的个体变异位数多,也就加大了其变异的搜索范围,使得种群的多样性也得到了提高。
2 算法设计与实现
2.1 自适应免疫遗传算法的设计
根据本文对基本遗传算法提出的改进思路,得到的自适应免疫遗传算法的算法流程图如图1 所示。其中,“提取疫苗”、“判断交叉变异算子是否调整”以及“对种群个体采取免疫操作”的相关操作流程见图2。
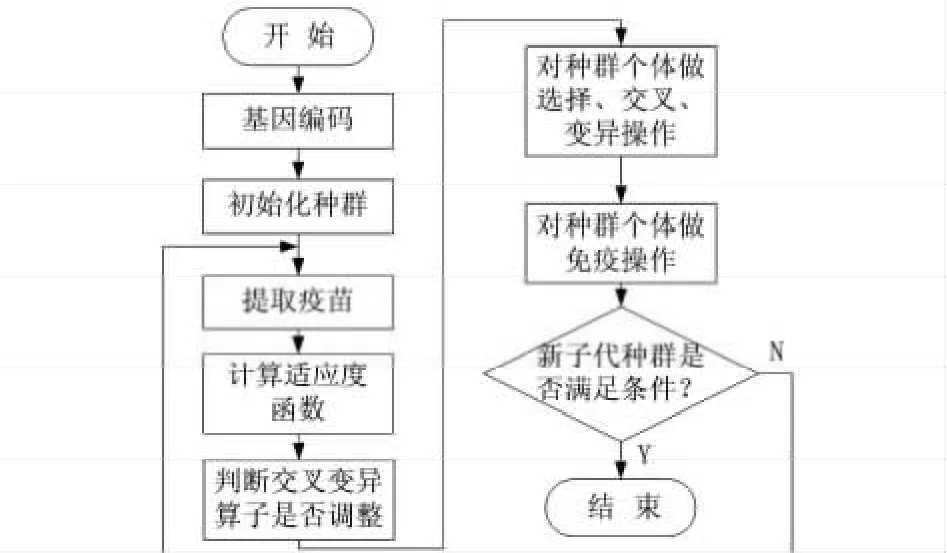
图1 自适应免疫遗传算法流程图Fig 1 Flowchart of adaptive immune genetic algorithm
本文的非线性变换函数选取了文献[6]提出的非完全Beta 函数,该函数可实现图像增强中的几种典型变换曲线的自动拟合。归一化的非完全Beta 函数F(u)定义为
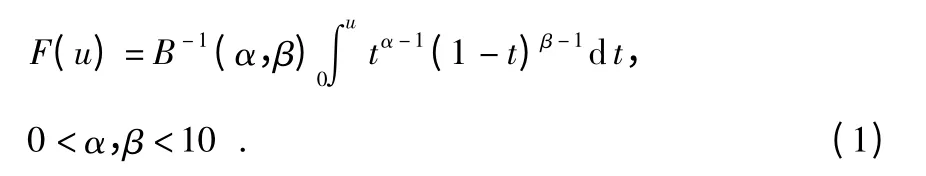
其中,B(α,β)为Beta 函数,表示如下
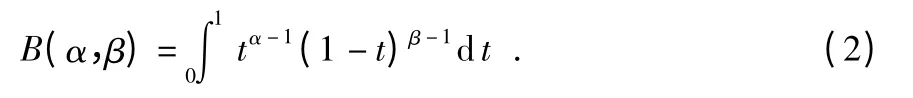
α,β 将采用本文提出的自适应免疫遗传算法确定。
2.1.1 编码设计
将参数取值范围[U1,U2]按照计算精度δ 分段,各分段处的实数根据线性映射关系均被转换为二进制数
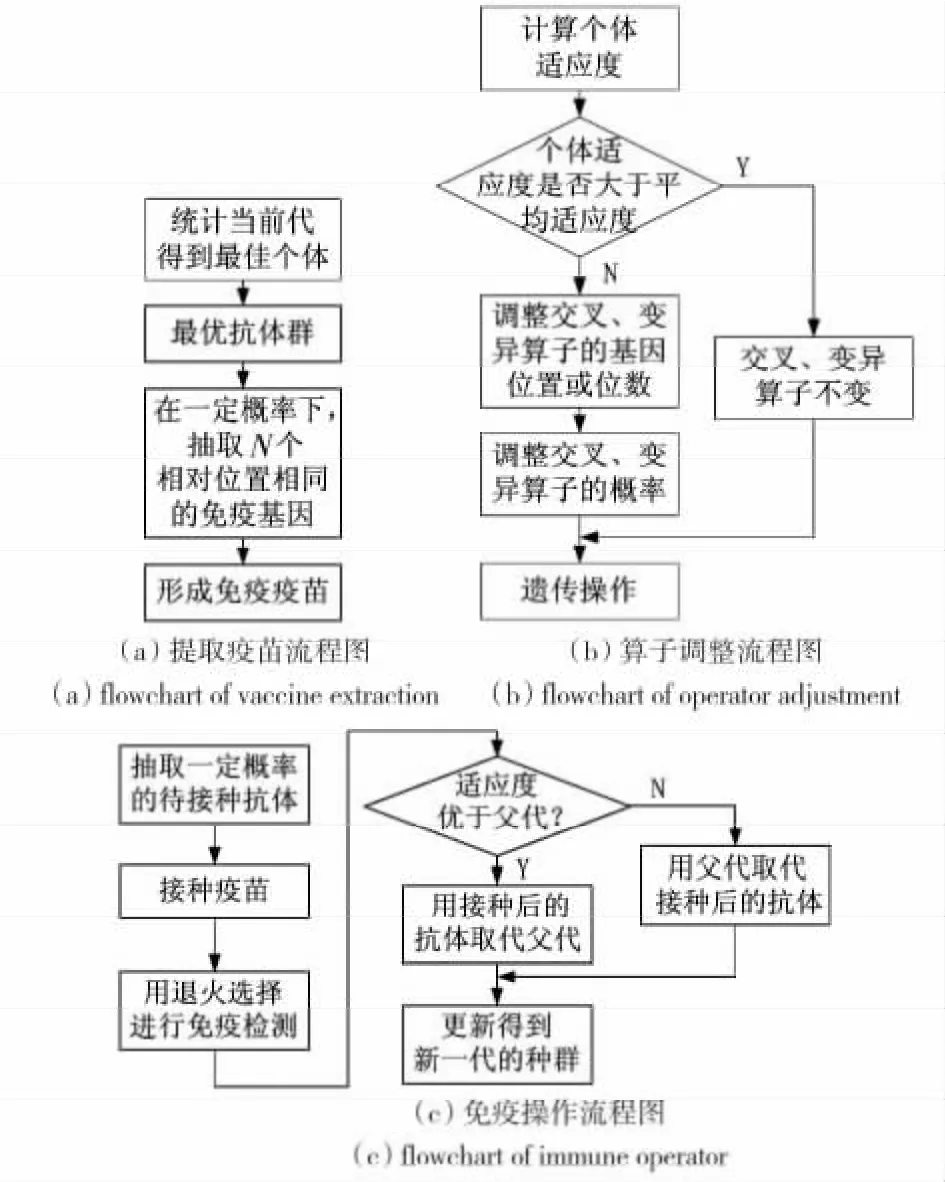
图2 相关操作流程图Fig 2 Flowchart of related operation

2.1.2 适应度函数设计
适应度函数设计包括三部分:
1)适应度函数的选取:本文算法的适应度函数选取了文献[7]提出的图像质量评价函数
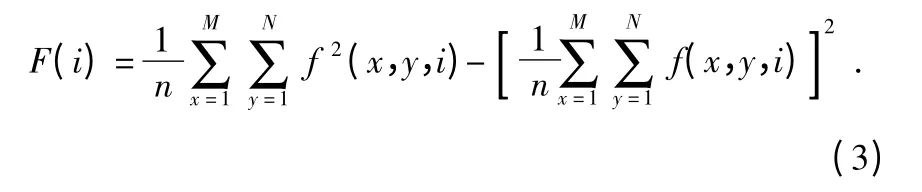
其中,M,N 为图像的宽和高,n=M×N,i 表示进化个体。
2)染色体解码:为了计算进化个体的适应度,需将二进制编码的染色体bkbk-1bk-2…b2b1解(记作Ri)解码并转换为参数取值范围内的实数值,解码公式如下
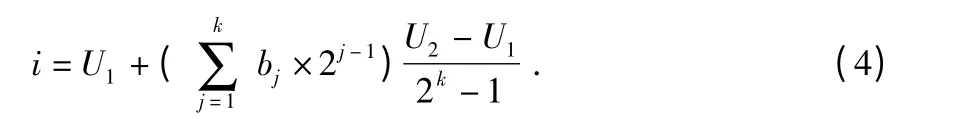
3)计算个体适应度:将由式(4)解码得到的进化个体i代入式(3)计算其适应度。
2.1.3 免疫遗传算子设计
1)选择算子
本文中选择算子采用轮盘赌选法,每个染色体Ri的累计概率Pi为
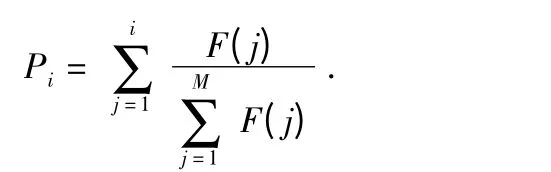
生成一个[0,1]间的随机数r,按照式(5)选择染色体Ri作为父代种群
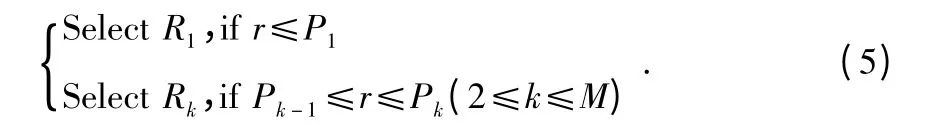
2)交叉算子
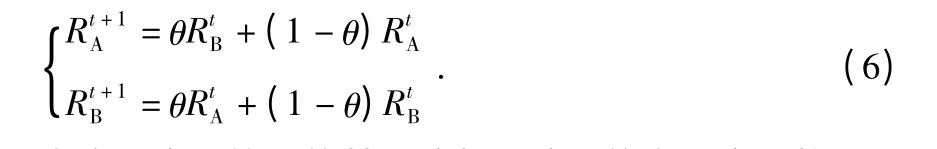
为实现交叉算子的基因位数和位置的自适应调整以及交叉概率的自适应调整,对概率参数θ 的选取满足式(7)

交叉概率Pc的选取满足式(8)
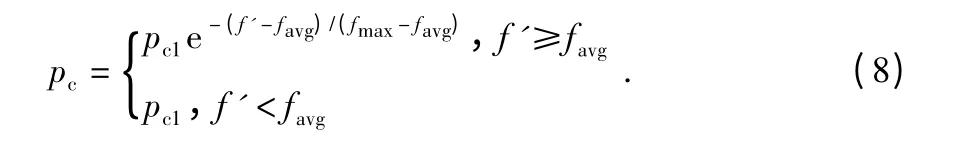
其中,fmax为群体中最大的适应度值,favg为每代群体的平均适应度值,f'为待交叉两个体中较大适应度值,pc1为最大交叉概率[8]。
3)变异算子
本文中变异算子采用多位变异法,种群个体的变异位数M 由式(9)决定

交叉概率pm的选取满足式(10)
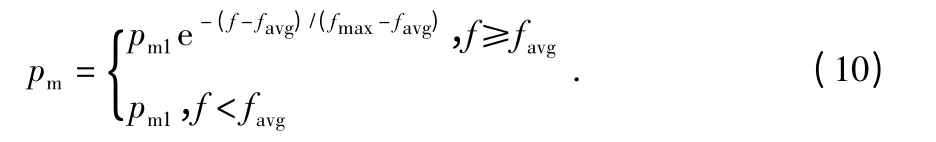
其中,f 为群待变异个体的适应度值,fmin为群体中最小的适应度值,pm1为最大变异概率。
4)免疫算子[9]
免疫算子由提取疫苗、接种疫苗、免疫检测和免疫选择等4 步操作完成。
提取疫苗:将当前种群中的最优个体与之前经进化保留下来的最优个体进行对比分析,选取具有公共特点和有效信息的某些基因位作为疫苗。
接种疫苗:按照一定比例a(0≤a≤1)随机抽取群体中N=M×a 个个体,用上述操作中提取的特定基因位去替换这些个体中的相应基因位,M 为初始种群的个体数量。
免疫检测:比较接种了疫苗的个体与其相应的父代个体的适应度,若父代适应度高,则保留父代个体;反之,则选取子代个体进入下一轮进化。
免疫选择:本文算法中的免疫选择采用了退火选择

其中,退火温度为T,Tk=ln(T0/k+1)),T0=100,k 为进化代数,f(xi)为接种了疫苗的个体xi的适应度,Tk是趋于0 的温度控制序列。
2.1.4 算法结束条件
算法结束条件采用连续几代群体的最优适应度函数值没有发生太大变化,或者算法迭代次数已达最大进化代数。
2.2 图像增强算法的实现
1)归一化:f(x,y)表示坐标为(x,y)的原始图像灰度值,在处理前先进行归一化处理
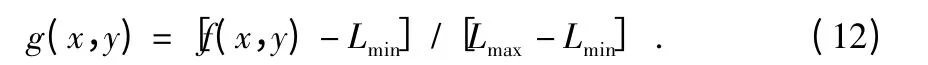
其中,Lmax,Lmin分别为该图像灰度的最大值和最小值。
2)非线性变换:非线性变换函数F(u)取式(1),得

其中,g'(x,y)中含有待定参数α,β,0≤g'(x,y)≤1。
3)种群初始化:设置初始种群规模M=20 和最大进化代数T=200,初始种群的生成采用均匀分布的随机数实现。
4)编码:参数α,β 的取值范围为[1,10],要求的精度是小数点后2 位,则根据2k+1<(10-0)×102<2k-1 可得α,β 采用二进制编码的位数均为10,让每条染色体包含两个基因段[α,β],则该染色体含20 个基因位。
5)自适应免疫遗传操作:设置最大交叉概率pc1=0.7和最大变异概率pm1=0.01,对种群依次实施选择、交叉、变异和免疫操作,并不断重复该步骤。
6)结束条件判断:如果T 达到最大进化代数或是最优适应度函数值F(i)没有发生太大变化,则把当前最优适应度值的个体[α,β]作为最优解输出。
7)计算灰度变换后的灰度值:将最优参数[α,β]代入g'(x,y)中,得到图像经非线性灰度变换后的灰度值。
8)去归一化:f'(x,y)为最终图像增强后的灰度值,则根据g'(x,y)的值可得到f'(x,y)
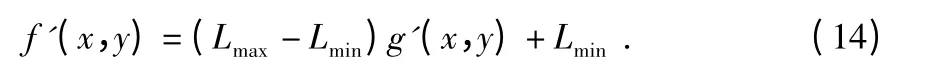
9)图像增强结果:将步骤(1)~(8)用Matlab 编程实现,将原始图像增强后的效果图输出。
3 仿真研究
3.1 本文算法的性能分析
本文采用平均进化代数、平均运行时间及无全局最解率作为评价指标,性能比较如表1。
由表1 可以看出:免疫遗传算法与本文算法在算法收敛速度和全局收敛方面的性能明显优于基本遗传算法,而本文算法较免疫遗传算法略胜一筹。
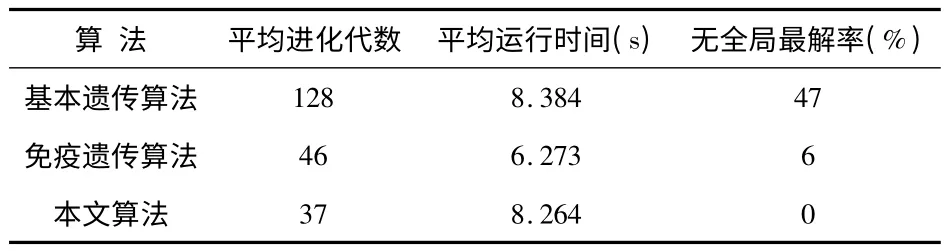
表1 各进化算法的性能比较Tab 1 Performance comparison of different evolutionary algorithms
3.2 图像增强效果的分析
为检验基于自适应免疫遗传算法的图像增强效果,在Matlab R2009b 仿真环境下实施图像处理,并从主观视觉效果对比与客观质量评价两方面来考核各算法。
3.2.1 主观视觉效果对比
对标准图像库中的“water lily”和“peppers”图像依次采用反锐化掩模法、直方图均衡化法和本文算法进行增强处理,得到的增强效果分别如图3 和图4 所示。
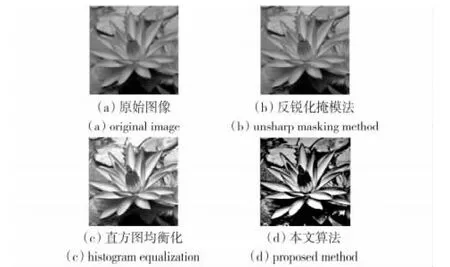
图3 water lily 增强前后的效果图Fig 3 Enhancement effect comparison of water lily

图4 Peppers 增强前后的效果图Fig 4 Enhancement effect comparison of peppers
图3 中原始图像视觉效果偏暗且边缘模糊,经反锐化掩模法处理的图像依旧偏暗,对比度不强。直方图均衡化法处理的图像灰度分布均匀,但是暗处细节表现不明显。本文算法处理得到的图像亮度适中,对比度强,细节丰富,例如:莲叶纹理和被遮挡的莲叶都有呈现。图4 中原始图像视觉效果偏亮,采用本文算法处理后,图像灰度动态范围变宽,暗处细节表现明显,有效提高了图像对比度,获得了更优的图像增强效果。
采用本文提出的自适应免疫遗传算法对非完全Beta函数中的参数 求取最优解,得到的最佳变换参数见表2。
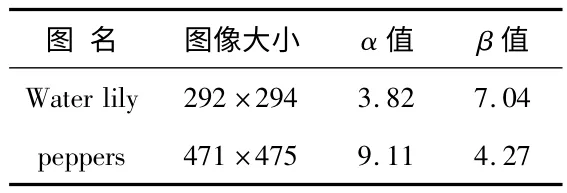
表2 本文算法取得的最佳变换参数Tab 2 The best transform parameters obtained by the proposed algorithm
根据表2 可得图Water lily 与图Peppers 的最佳灰度变换曲线,如图5 所示。
由图5 可以看出:当α=3.82,β=7.04 时,小部分较低灰度值在函数y=x 以下,大部分较高灰度值在函数y=x以上,说明原始图像偏暗,需对原始图像的较暗区域进行拉伸,使图像的灰度范围分布更加均匀;当α=9.11,β=4.27时,大部分较低灰度值在函数y=x 以下,小部分较高灰度值在函数y=x 以上,表明原始图像偏亮,需对原始图像的较亮区域进行拉伸,以便提高视觉效果。
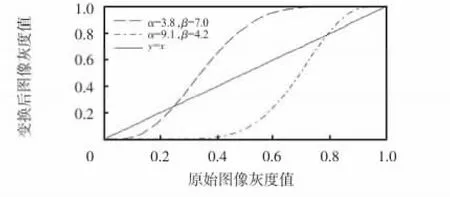
图5 图Water lily 与图Peppers 的灰度变换曲线Fig 5 Gray level transformation curves of water lily and peppers
3.2.2 客观质量评价
为了定量描述图像增强效果,本文采用均值、标准差、信息熵这三个评价指标来分别反映图像的明暗度、对比度以及信息量[10],实验数据分别见表3 和表4。
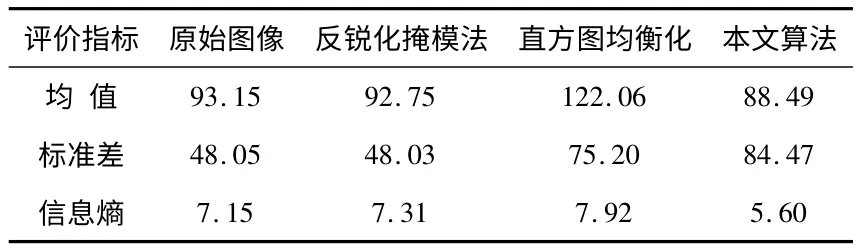
表3 图Water lily 评价标准Tab 3 Evaluation standard of water lily

表4 图Peppers 评价标准Tab 4 Evaluation standard of peppers
从表3 数据可以看出:原始图像均值、标准差均较小,说明该图视觉效果偏暗且对比度不强。反锐化掩模法处理后的图像均值、标准差变化不大,说明增强效果一般;直方图均衡化法处理后的图像均值和标准差明显增大,说明图像视觉效果被提亮,对比度也增强了;本文算法处理后的图像标准差最大说明对比度最强,但是也由于这个原因致使均值降低。从表4 数据可以看出:原始图像均值偏高,标准差较小,说明该图视觉效果偏亮且对比度不强,均值与标准差的分析与表3 类似,这里不再赘述。
4 结束语
1)借鉴生物免疫系统自适应识别功能,将免疫算子引入与遗传算子相结合,克服了种群优化过程中出现的退化现象。
2)在种群进化过程中根据个体适应度动态调整交叉、变异算子的基因位数及各操作算子的概率,使种群个体多样性增强,克服了算法陷入局部最优解的现象,并且提高了算法的收敛速度。
将该算法应用到图像增强中,可实现图像增强效果的自适应调整,并能拓宽灰度动态范围,凸显暗处细节,提高图像对比度,使图像增强效果更加明显。
[1] 冈萨雷斯.数字图像处理[M].2 版.阮秋琦,译.北京:电子工业出版社,2003:59-61.
[2] 张 懿,刘 旭,李海峰.自适应图像直方图均衡算法[J].浙江大学学报:工学版,2007,41(4):630-633.
[3] Zheng Yufeng,Edward A Essock.A local-coloring method for night-vision colorization utilizing image analysis and fusion[J].Information Fusion,2008,9(2):186-199.
[4] 田 莹,苑玮琦.遗传算法在图像处理中的应用[J].中国图像图形学报,2007,12(3):390-391.
[5] 郑 军,诸 静.基于自适应遗传算法的图像匹配[J].浙江大学学报,2003,37(6):689-692.
[6] Tubbs J D.A note on parametric image enhancement[J].Pattern Recognition,1997,30(6):617-621.
[7] 黄 楠.遗传算法在图像增强中的应用研究[J].计算机仿真,2012,29(8):261-264.
[8] 李顺康,李茂明,张文生.一种基于改进遗传算法的图像分割方法[J].计算机应用研究,2009,26(11):4364-4367.
[9] 段玉波,任建伟,霍凤财,等.一种新的免疫遗传算法及其应用[J].控制与决策,2005,20(10):1185-1188.
[10]胡韦伟,汪荣贵,方 帅,等.基于双边滤波的Retinex 图像增强算法[J].工程图学学报,2010,31(2):104-109.

