一种用于PID 控制参数优化的混合果蝇算法*
宋 娟
(宁夏大学 物理电气信息学院,宁夏 银川750021)
0 引 言
PID 控制是最早发展起来的控制策略之一[1],但随着现代工业系统非线性复杂程度的提高和被控对象不确定性因素的增加,传统的PID 优化方法往往难以达到满意的控制效果[2]。针对不稳定被控对象的PID 控制系统,迄今为止,许多智能优化技术已经应用于此,例如:遗传算法(GA)[3]、粒子群优化(PSO)算法等[4,5]。相对于GA,PSO算法具有更快的收敛速度[6],但存在易陷入局部极值、运行后期收敛速度变慢等缺陷。
果蝇优化算法(fly fruit optimization algorithm,FOA)是新近提出的一种基于果蝇觅食行为寻求全局优化的智能优化算法[7,8]。相对于标准PSO 算法,FOA 较为适合复杂问题的优化求解,但是其应用于非稳定对象的PID 控制参数整定目前研究较为少见。通过分析可知,FOA 中果蝇移动的距离与方向较为随机,导致果蝇味道浓度判定值的表达形式过于单一化和不确切,算法运行后期搜索的盲目性较大、寻优结果精度低,从而影响了该算法搜索的质量和效率。
为了弥补FOA 存在的一些缺陷,本文采用分段优化的思想,在FOA 优化后期引入具有良好收敛特性的PSO 算法,用来优化果蝇个体飞行距离和味道浓度判定值,提出一种混合FOA(hybrid FOA,HFOA),实现一类不稳定受控对象的PID 控制参数自整定。仿真结果证明:该算法稳定性、计算效率和寻优精度优于标准的FOA 和PSO 算法,应用于PID 控制器参数优化效果良好。
1 PID 控制参数的设计
PID 控制器一般形式为

其中,e(t)为系统误差;u(t)为控制器输出信号;Kp,Ki和Kd分别为对系统误差信号及其积分与微分量的加权,控制器通过这样的加权就可以计算出控制信号,驱动受控对象。如果控制器设计合理,那么控制信号将能朝误差减小的方向变化,达到控制要求[9]。
采用HFOA 整定PID 控制器参数,必须建立综合评价各项性能指标的适应度函数,采用ITAE(积分准则)作为系统性能评价函数

选取被控对象为以下不稳定系统[10]

在Simulink 环境建立的仿真模型如图1 所示。图中的微分环节由一个一阶环节近似,输出端口即为式(1)所示的ITAE 指标,通过将时间与误差绝对值的乘积进行积分后得到。

图1 PID 控制器的SimuLink 模型Fig 1 SimuLink model of PID controller
对于PID 控制器的整定,从优化的角度来说,就是在Kp,Ki和Kd这3 个参数中寻找最优值,使系统的性能达到最优,输出良好的阶跃响应曲线。由于面向的是一类不稳定被控对象,本文采用时域动态性能指标(包括调节时间ts、上升时间tr、峰值时间tp和最大超调量σ%)侧重评价系统的动态性能。
2 FOA 基本原理
FOA 起源于对简单社会系统的模拟,最初是模拟果蝇觅食的过程,通过群体中个体之间的合作与竞争来对其搜索过程进行指导,从而实现对复杂优化问题的求解。
FOA 优化流程如图2 所示。FOA 具有原理简洁和计算高效等优点,较为适合对PID 控制参数进行优化。但算法本身果蝇个体飞行距离取值较为随机,直接影响到味道浓度判定值的表达形式,从而削弱了全局性能和收敛精度。为了提高FOA 优化性能,本文考虑引入收敛稳定度较好的PSO 算法来改善FOA 的优化性能。
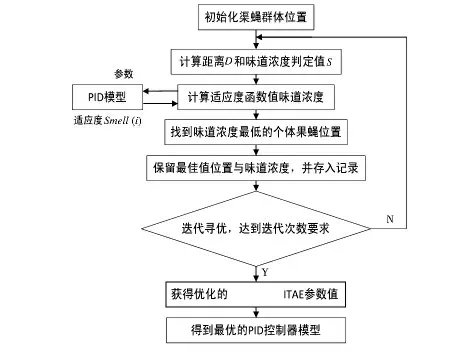
图2 FOA 算法优化流程Fig 2 Flowchart of FOA algorithm
3 HFOA 算法优化PID 控制器设计
3.1 POS 算法基本原理
PSO 算法由Eberhert R C 和Kennedy J 于1995 年共同提出,源于对鸟群觅食行为的研究[11~13]。PSO 算法是根据全体粒子和自身的搜索经验向着最优解的方向“飞行”,在进化过程中粒子群多样性会下降,因此,当算法收敛到一定精度时,无法继续优化容易陷入局部最优,造成所能达到的精度较差[13]。
PSO 算法实现由式(4)、式(5)确定

其中,粒子数目i=1,2,…,n;D 维搜索空间d=1,2,…,D;X 表示粒子的位置;V 表示粒子的速度;w 为惯性因子;c1,c2为加速常数;r1,r2为[0,1]区间的随机数;Pid为粒子当前搜索到的最优位置;Pgd为整个粒子群当前搜索到的最优位置。
3.2 HFOA 的优化过程
在优化过程初期虽然具有较快的收敛品质,但是后期却往往收敛较慢,或者无法达到要求的精度。为了提高FOA 优化PID 控制器的性能,HFOA 采用了分段优化的思想,将FOA 与PSO 算法相结合,在合适的时候互相切换,实现二者优缺点互补,在提高收敛速度的同时,能适当提高收敛精度,并且还能在一定程度上克服局部极值的问题。
HFOA 整定PID 的基本思想是:在优化过程初期,利用FOA 得到果蝇群体最优浓度值Smell、味道浓度判定值S 和携带最优食物浓度果蝇的位置X 和Y;在优化过程后期,采用PSO 算法对FOA 中果蝇个体飞行距离和味道浓度判定值进行进一步优化,从而利用HFOA 在未知参数Kp,Ki和Kd所有可能取值组合的可行解集合中找出最优解,使定义的适应度函数ITAE 最小。
利用HFOA 对PID 控制器的参数进行优化步骤如下:
1)随机初始果蝇个体位置X 和Y,果蝇个体用嗅觉搜寻食物的随机方向与距离X(i)和Y(i)。
初始化PSO 算法参数:惯性因子w,加速常数c1,c2,粒子速度Vmax,Vmin。
2)计算与原点之间距离D(i),再求出味道浓度判定值S(i)(取距离倒数),形成如下形式的编码串:S(i)=(Kp,Ki,Kd)。
3)由S(i)代入味道浓度判定函数以求出该果蝇个体位置的味道浓度Smell(i)=Function(S(i))。
4)根据初味道浓度寻找初始极值,利用视觉寻找伙伴聚集味道浓度最低的个体果蝇位置,并保留最佳值初始位置与初始味道浓度
[bestSmell,bestIndex]=min(Smell(i))
X=X(bestIndex,:)
Y=Y(bestIndex,:)
5)令个体最优位置Pbest=S,群体最优位置Pgbest=S(bestIndex,:),粒子位置Xpos1=S(i),Xpos2=X(i),Xpos3=Y(i);个体最优极值fPbest=Smell,群体最优极值fPgbest=Smell(bestIndex,:)。
6)更新粒子的位置和速度,按照式(4)和式(5)确定。
7)运行控制系统模型,求出种群中各个体的适应度函数值Smell(i)=Function(S(i))。
8)判断当前适应值if Smell(i)<fPbest,个体更新操作;if Smell(i)<fPgbest,群体更新操作;更新果蝇最佳位置X 和Y。
9)进人迭代寻优,重复执行步骤(6)~(8),并判断是否满足终止条件;否则,退出算法,得到最优解。
4 仿真实验与结果分析
4.1 仿真条件设置
设置FOA 的初始条件如下:最大代数50,种群规模100。PSO 算法初始条件设置[14]:惯性因子w=0.6,加速常数c1=c2=2,初始化粒子速度范围[-1,1],Kp,Ki和Kd三个待优化参数的搜索范围均为[0,300],粒子群规模为100,最大迭代次数为50。控制系统仿真时间0∶10。
4.2 FOA,PSO,HFOA 优化性能比较
为了验证HFOA 优化PID 参数的收敛精度和稳定性,每种算法连续在MatLab 7.8a 环境下运行5 次,图3(a),(b),(c)为FOA,PSO,HFOA 连续5 次寻优过程。
如图3(a),(b),(c)所示,FOA 5 次搜索到的最优解分别为3.9414,3.9382,5.7635,3.9448,4.18,每次收敛值都不同,说明FOA 在PID 参数优化过程中保持探索与开发平衡的能力较差;HFOA 运行5 次,最终都收敛于最优解1.042 4,而PSO 算法运行5 次,只有3 次搜索到最优解1.042 4,2 次收敛于局部最优解1.085 2。仿真结果表明:HFOA 相对于标准PSO 和FOA 在优化PID 控制器上稳定性更好,而FOA 收敛全局最优的稳定度最差;FOA 的收敛精度较PSO 和HFOA 低,表明FOA 运行后期搜索的盲目性较大,较PSO 算法更容易陷入“早熟”。

图3 PID 控制器的ITAE 优化曲线Fig 3 Optimization curve of PID controller in ITAE
为了比较FOA,HFOA 和PSO 算法优化PID 参数的计算效率、搜索质量和整定后系统的输出响应,程序分别运行得到一次优化结果,设置群体数量100 迭代50 次。计算结果见表1,动态特性见表2,果蝇群体寻优轨迹见图4,系统仿真输出见图5。
由表1 得出,FOA 仿真计算时间为123.939 s,PSO 算法运算时间为209.095 4 s,而HFOA 为119.448 5 s。HFOA 和标准FOA 求解速率上相差不多,较PSO 算法运算量要小很多。这表明HFOA 在PID 参数优化计算上效率明显优于标准PSO 算法。
图4 中横轴和纵轴没有具体单位,只是果蝇优化飞行路径坐标变化曲线,这个坐标和寻优解(味道浓度判定值)之间是有关系的,得到的飞行路径实际上是寻找最优解S(kp,Ki,Kd)的变化曲线;对比图4(a),(b),HFOA 相对于FOA 果蝇群体的寻优轨迹更加集中,解空间更大,果蝇群体密集度更高。表明HFOA 对解空间探索与开发平衡的能力较FOA 更强,搜索质量更高。

表1 三种算法优化PID 的控制参数Tab 1 Optimization PID control parameter of three algorithms

表2 三种算法作用下系统动态特性比较Tab 2 Comparison of system dynamic characters of three algorithms
FOA,PSO 和HFOA 整定PID 控制器系统的输出响应曲线见图5,纵坐标的含义为PID 控制系统在单位阶跃输入信号作用下,系统的动态响应输出信号。从图中可以看出:系统在三种算法作用下,均经过PID 控制器调整后,再经过反馈最终都达到稳定状态。由表2 得出,采用HFOA 优化PID 控制器,系统的超调量σ%和调节时间ts较FOA 和PSO 算法明显减少,控制效果更好。

图4 果蝇群体的寻优轨迹Fig 4 Optimization hunting track of fly fruit swarm

图5 三种算法优化参数的单位阶跃响应曲线Fig 5 Unit step response curve of optimization parameter of three algorithms
5 结束语
针对常规PID 控制方法的不足,通过分析FOA 的优化原理,本文提出了一种HFOA 来整定PID 控制参数,获得了较好的控制效果和收敛特性。HFOA 不仅集成了FOA 计算高效和PSO 算法收敛稳定的优点,同时可有效地避免FOA和PSO 算法陷入“早熟”。MatLab 仿真结果表明:该算法能较快地搜索到最优解,且整定后的PID 控制器调节时间快、超调量小,具有更好的稳定性,系统动态性能得到较大改善,对于一类不稳定控制系统具有良好的控制性能。
[1] Bennett S.Development of the PID controllers[J].IEEE Control Systems Maganize,1993,13(6):58-65.
[2] 刘金棍.先进PID 控制MatLab 仿真[M].北京:电子工业出版社,2006:161-163.
[3] 方彦军,易凤飞,胡文凯.基于遗传算法的广义预测PID 控制及其在锅炉主汽温系统中的应用[J].武汉大学学报:工学版,2013,46(3):386-392.
[4] 孟 杰,陈庆樟,张 凯.基于粒子群算法的汽车悬架PID 控制仿真[J].计算机仿真,2013,30(4):155-158,168.
[5] 杜文正,谢 政,童国林.基于粒子群优化算法的桥式起重机PID 控制参数优化[J].计算机测量与控制,2013,21(2):371-373,401.
[6] Eberhart R C,Shi Y H.Comparison between genetic algorithms and particle swarm optimizatnion[C]∥Proceedings of the 7th International Conference on Evolutionary Programming,VII EP’98,San Diego,California,1998:611-616.
[7] 潘文超.果蝇最佳化演算法[M].台北:沧海书局,2011.
[8] Pan Wen Tsao.A new fruit fly optimization algorithm:Taking the financial distress model as an example[J].Knowledge-Based Systems,2012,26:69-74.
[9] 薛定宇.控制系统仿真与计算机辅助设计[M].2 版.北京:机械工业出版社,2010:234-235.
[10]薛定宇,陈阳泉.控制数学问题的Matlab 求解[M].北京:清华大学出版社,2007:379-381.
[11]Kennedy J,Eberhart R C.Particle swarm optimization[C]∥IEEE International Conference on Neural Networks,Piscataway,NJ:IEEE Service Center,1995:1942-1948.
[12]Kennedy J,Eberhart R C.A new optimizer using particles swarm theory[C]∥Proceedings of the Sixth International Symposium on Micro Machine and Human Science,Piscataway,NJ:IEEE Service Center,1995:39-43.
[13]邓 丽,蒋 睛,费敏锐.基于免疫粒子群算法的PID 参数整定与自适应[J].自动化仪表,2013,34(2):65-67,71.
[14]史 峰,王 辉.MatLab 智能算法30 个案例分析[M].北京:北京航空航天大学出版社,2011:133-156.

