小波分析在激光测距传感器中的应用

薛缠明，李丽宏

(太原理工大学 信息工程学院，山西 太原030024)

0 引 言

目前，国家对车辆超限的治理已有了严格的要求。此前在车辆宽高超限检测中都是靠人工测量完成，不仅影响车辆的行驶进度，而且测量效率较低。为了精确快速地检测车辆的宽高和提高道路的畅通性，开发了单传感器激光车辆宽高检测系统。在使用的过程，发现测量信号中掺杂有高频车辆边缘光噪声，导致测量精度明显下降［1］。甚至会影响到车辆是“正常”还是“超宽超高”的判断和车辆的正常通行。小波分析具有多分辨率分析的特点，并在时域和频域都具有表征信号局部特性的能力［2］。

针对上述出现的问题，本文提出以小波分析法为基础利用边缘光噪声的特性准确定位出光噪声的精确范围，进一步有效地去除它对车辆准确性测量的影响。

1 激光车辆宽高检测系统

激光车辆宽高检测系统如图1 所示，激光传感器发射激光遇到被测物体后发生反射，传感器接收到反射光，经过计算得出被测物体位置的极坐标［3］。该激光车辆宽高检测系统是把激光传感器安装在龙门架中间，经过实验合理设置传感器扫描角度和分度。当有车辆进入检测区域时，激光传感器以50 Hz 的频率扫描，每个周期可以得出一组车辆的宽度和高度值，当汽车完全通过时，通过比较所有数值得出车辆的最宽值和最高值计入数据库。

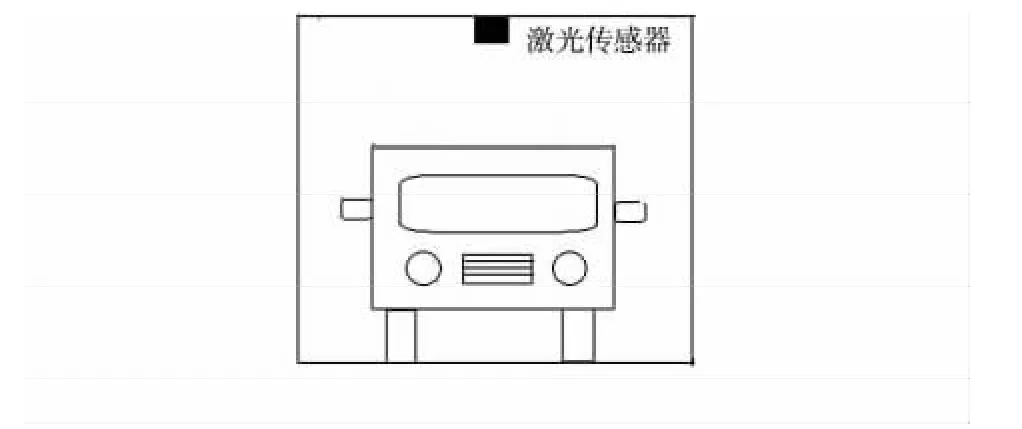
图1 激光车辆宽高检测系统图Fig 1 Laser width-height detection system of vehicle

2 小波分析法

目前在系统信号检测中小波分析方法凭借它在时域和频域同时具有良好的空间局部化性质，已经成为信号检测的重要工具。在实际的信号中，噪声通常表现为高频信号，而有用信号通常表现为低频或者平稳信号［4］。基于上述噪声信号的特性，可以利用小波变换通过伸缩平移运算对信号逐步进行多尺度细化，在高频处利用时间细分和可以聚焦在任意高频细节的优点，对原始信号进行小波分析和噪声信号的定位。在利用小波分析对原始信号去除噪声过程中，最理想的结果是有效地保留有用信息，且去除掺杂的干扰噪声，所以，在小波分析中小波函数和阈值的选择变成了关键环节。为此，提出一种以小波分解为基础去除噪声的方法，其可分为三个步骤:

1)对测量信号作小波分解

选择一个小波的基函数ψ(t)和小波分解中小波系的阶数D，其中，ψ(t)为平方可积，即ψ(t)∈L2(R)，对原始信号进行D 阶分解后，可以利用鼻尖细节部分准确定位出高频信号的范围。

2)光噪声定位

对原始信号进行D 阶分解后，根据噪声信号的幅值和频率特性，对信号细节部分进行阈值判断，准确地判别出光噪声在信号中的具体范围。

3)数据检测

对信号进行小波分解和高频光噪声准确定位后，对信号进行重构出完整的有用信息。通过Matlab 仿真，便可直观地看到重构后信号。

2.1 小波函数选择与分解

在激光宽高检测系统中，车辆实际信号通常表现为低频信号或是一些比较平稳的信号，而边缘光噪声则通常表现为特定的高频信号。Daubechies 小波是由世界著名的小波分析学者Inrid Daubechies［5］构造的小波函数，应用它对原始信号进行分解时随着阶次增大，消失矩阶数越大，频带划分效果越好，并且提供了比其它函数更有效的分析和综合能力［6］。

设原始信号为f(t)，它的序列为{f(t)，n=1，2，…，N}。若以{f(n)，n=1，2，…，N}表示信号f(t)在尺度j=0 时的近似值，A0(n)=f(n)，则f(t)的小波变换由以下两个公式确定

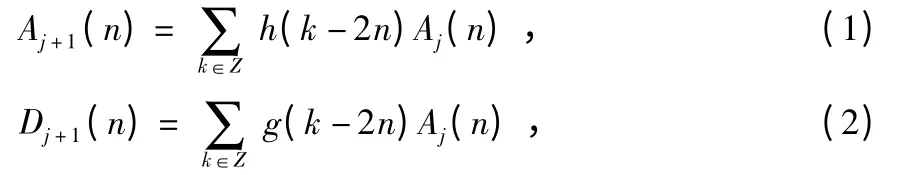
式中 h(n)和g(n)为由小波函数ψ(t)确定的一对互补的共轭滤波器，其中，h(n)为低通滤波器，g(n)为高通滤波器。因而，Aj，Dj分别称为信号在尺度j 上的逼近部分(低频)和细节部分(高频)。离散信号A0经过尺度1，…，j 的分解，最终分解为D1，D2，…，Dj，Cj它们分别包含了信号从高频到低频的不同频带信号，即信号的小波的分解就是相当于信号不断经过两个低通和高通滤波器对其近似部分进行滤波的结果。

对于三级分解，原始信号f(t)可分为

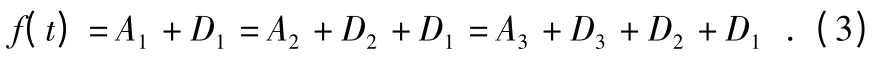
结合激光宽高检测系统实际使用得出的噪声频率特性，选择利用Daubechies 小波进行三级分解。

2.2 光噪声的定位

光噪声是指对于车辆实际值的随机偏离。利用小波分析法窗口面积固定，但形状可以改变，在低频部分具有较高的频率分辨率和较低的时间分辨率，在高频部分具有较高的时间分辨率和较低的频率分辨率的特点。对原始信号进行小波分解后，在大尺度下，可以将信号的低频信息(全局)表现出来，在小尺度下，可以将信号的高频(局部)特征反映出来。

基于上述原理，通过跟踪小波变换在细尺度下的模极大曲线方法检测原始信号中高频信号的位置;再根据实际实验中光噪声的幅值与车辆实际平稳信号幅值偏差阈值Δδ≤300 和车辆边缘的位置来准确判断光噪声的范围。

2.3 数据检测

以山西某国道超限检测站车辆数据为例，取出车辆通过激光车辆宽高检测系统时采集的一个周期的数据，通过小波分解和光噪声定位后，对处理后的信号进行重构，采用Matlb 中利用工具箱函数利用wavedec()函数进行小波分解仿真实验［7］。wavedec()的调用格式为

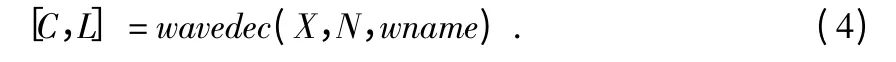
其中，［C，L］为小波分解输出值，X 为一维信号，N 为分解的层数，wname 为使用的小波函数。原始信号如图2所示。

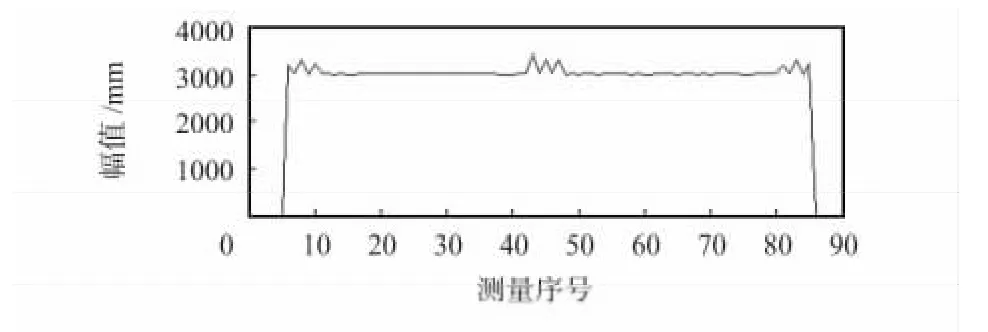
图2 原始信号Fig 2 Original signal

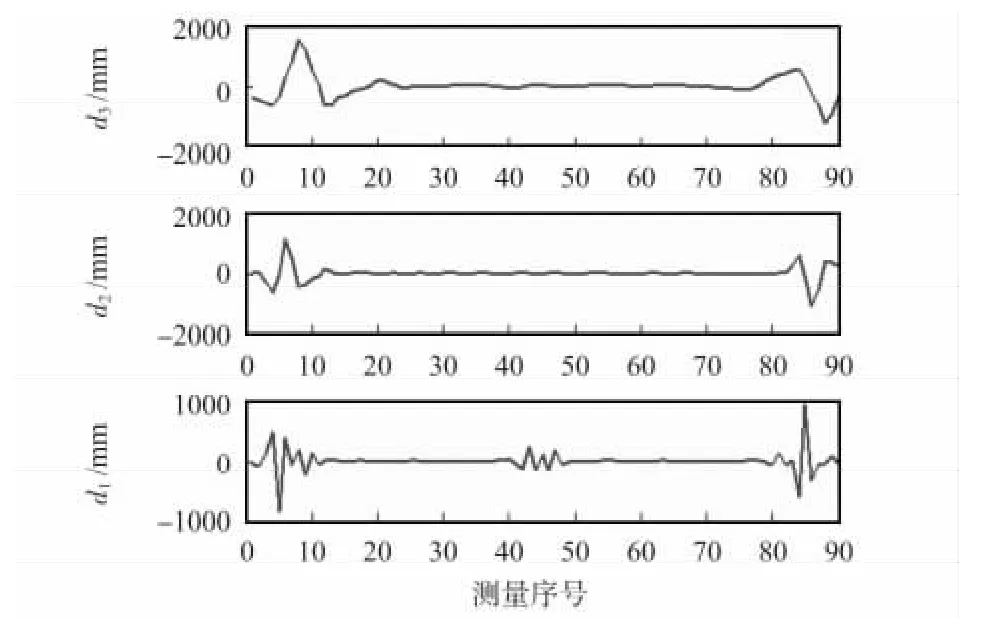
图3 用db3 小波进行5 层分解后的第1 ～3 层细节系数Fig 3 Detail coefficients of 1 ～3 layers after decomposition 5 layers with db3 wavelet

对原始信号小波三级分解后的第1 ～3 层细节系数，如图3 所示。经过三级分解，发现在第1 层细节系数d1中明显定位出高频信号的位置，再利用实验得到的幅值偏差阈值Δδ≤300 进行判断，如果定位出的位置幅值在偏差阈值范围内，且在车辆信号的边缘，便可认为是光噪声;否则，认为是车辆的实际高频信号，最后去除判断出的范围，对信号进行重构，得到重构后的信号如图4。

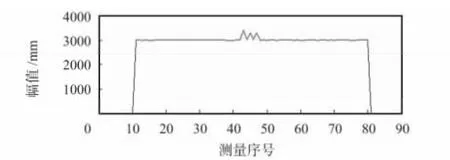
图4 重构后的信号Fig 4 Reconstructed signal

3 结 论

本文将小波分析理论应用到智能测量宽高检测系统中，经过仿真和实际使用，对原始信号进行小波分解、阈值判断和重构。结果表明:小波分析法可以有效地消除高频光噪声的影响，有利于提高系统的精度。

［1］ 李永强，盛业华，刘会云，等.激光扫描点图像背景交互式滤除［J］.测绘科学，2008(1):130－250.

［2］ 权爱娟.小波分析在一维奇异信号检测应用中的应用研究［D］.德州:德州学院，2012.

［3］ 陈元朝，李丽宏.自适应滤波算法在车辆宽高检测系统中的应用［J］.中国测试，2014(2):40－43.

［4］ 张小飞，徐大专，齐泽锋.基于小波变换奇异信号检测的研究［J］.系统工程与电子技术，2003(7):814－855.

［5］ Ingrid Daubechies.Ten lectures on wavelets［C］∥CBMS－NSF Regional Conference Series in Applied Mathematics，Philadelphia:SIAM ED，2007:56－62.

［6］ 刘正平，冯召勇，杨卫平.基于小波去噪的微弱信号提取［J］.制造业自动化，2010(8):98－101.

［7］ 董长虹.Matlab 小波分析工具箱原理及应用［M］.北京:国防工业出版社，2009.