一缝洞型油藏溶洞临界垮塌深度预测模型及其应用

王 超, 张强勇, 刘中春, 袁圣渤, 张绪涛,3, 王有法

(1.山东大学岩土与结构工程研究中心,山东济南 250061; 2.中国石化石油勘探开发研究院,北京 100083;3.聊城大学建筑工程学院,山东聊城 252059)

一缝洞型油藏溶洞临界垮塌深度预测模型及其应用

王 超1, 张强勇1, 刘中春2, 袁圣渤1, 张绪涛1,3, 王有法1

(1.山东大学岩土与结构工程研究中心,山东济南 250061; 2.中国石化石油勘探开发研究院,北京 100083;3.聊城大学建筑工程学院,山东聊城 252059)

为钻前对缝洞型油藏是否垮塌进行预测,以塔河缝洞型油藏为背景,提出确定溶洞临界垮塌埋深的二分深度折减法,分析溶洞垮塌对多因素的敏感性,通过多元回归分析建立溶洞临界垮塌深度随顶板厚度、洞跨和侧压力系数变化的预测公式。对大量工况的数值进行计算分析,获得不同形态、不同尺寸溶洞的垮塌破坏过程、垮塌破坏模式、垮塌影响范围以及垮塌深度的变化规律,利用建立的溶洞垮塌深度预测公式对塔河油田实际分布的溶洞进行预测分析。结果表明:矩形和城门洞形溶洞为竖向剪切破坏,而圆形溶洞产生压实破坏;溶洞垮塌影响范围随顶板厚度和洞跨的增加而增大,最终趋于稳定,最大垮塌影响范围约为2.6倍洞跨;洞跨是影响溶洞垮塌的最敏感因素,其次为顶板厚度,侧压力系数对溶洞垮塌的影响最不敏感;溶洞的顶板厚度越大,溶洞越不容易出现垮塌;圆形溶洞最稳定,城门洞形溶洞次之,矩形溶洞稳定性最差。预测结果与油田生产实际相吻合。

缝洞型油藏; 临界垮塌深度; 二分深度折减法; 溶洞垮塌模式; 垮塌深度预测模型

在奥陶系碳酸盐岩储层中,裂缝-溶洞型储层是其中一类重要的储层,主要发育于石灰岩储层中。次生的溶蚀孔洞以大型洞穴为特征,是主要的储集空间,裂缝既是储集空间也是联通孔洞的通道[1-2]。根据钻井和录井资料,地下未充填溶洞能达到几米甚至更大,充填溶洞能达到几十米。但是在油藏开发过程中,根据部分油井生产动态推测,若井下发生部分溶洞坍塌或大裂缝出油通道闭合,会严重影响油井产量[3-4]，因此开展对于现今埋藏于地下的碳酸盐岩洞穴是否垮塌的预测评价具有重要理论意义和工程应用价值。针对缝洞型油藏,前人做了大量的研究[5-10]。虽然针对缝洞型油藏在开发技术、垮塌现象描述、漏失机制等方面已取得一些成果,但关于缝洞型油藏垮塌深度的定量认识还比较模糊。笔者从数值模拟角度出发,借助岩石破裂过程分析软件(RFPA),建立确定缝洞型油藏溶洞垮塌深度的二分深度折减法,获得不同洞型溶洞的垮塌破坏形态、垮塌影响范围及其垮塌深度,并通过多元回归分析建立多因素影响下溶洞临界垮塌深度的预测模型,为塔河缝洞型油藏石油开采提供理论依据。

1 溶洞临界垮塌深度分析方法

1.1 数值分析模型与计算条件

溶洞发育在奥陶系,溶洞上部奥陶系的碳酸盐岩顶板厚度在几米到几十米不等;洞周围岩石属于非常致密的泥晶灰岩,基质孔隙度和渗透率非常低。影响溶洞垮塌的主要因素有溶洞洞跨L、顶板厚度h、侧压力系数K。对缝洞型油藏中溶洞进行概化处理,不考虑溶洞充填状况,溶洞形态简化成矩形、城门洞形和圆形分析。根据地下溶洞的受力及变形特点,对所采用的计算模型进行简化处理,考虑到地下溶洞尺寸保持不变,且沿洞轴向方向受力不变,采用平面应变模型对溶洞垮塌进行数值计算分析。

图1为溶洞的数值分析模型及边界条件。图1中溶洞顶板上覆岩层重力引起的附加应力用地层平均容重γ与溶洞实际埋深H相乘的竖向应力(P=γH)代替。模型左右边界施加水平应力,根据文献资料[11]知:水平应力梯度取值为Th=15.5 kPa/m,竖向应力梯度取值为Tv=25 kPa/m,侧压系数K=0.62。数值计算溶洞尺寸和实际溶洞尺寸一致,考虑边界约束效应,溶洞左右两侧和洞底以下取5倍的洞径。底面为固定边界。

图1 溶洞数值分析模型及边界条件Fig.1 Numerical model and boundary conditions of karst cave

根据文献[11]～[15],碳酸盐岩的物理力学参数取值:容重为7 kN/m3,泊松比为0.25,弹性模量为36.3 GPa,抗压强度为74.2 MPa,抗拉强度为3.8 MPa,内摩擦角为36.05°,黏聚力为2 MPa。

1.2 溶洞垮塌判据

采用基于有限元的RFPA软件计算分析溶洞的垮塌破坏,该软件通过将细观力学与数值方法有机结合,考虑岩石性质的非均匀性特点,模拟岩石变形和破裂的非线性行为,是一种用连续介质力学方法解决非连续介质力学问题的新型数值分析工具。通过考虑材料破坏后单元的参数弱化(包括刚度退化),模拟材料破坏的非连续和不可逆行为。借助此软件可计算并动态演示岩体从受载到破裂的完整过程[16-17]。图2为矩形溶洞垮塌破坏过程。

图2 矩形溶洞垮塌破坏过程Fig.2 Collapse-failure process of rectangle cave

由图2可以看出,RFPA计算软件可以很好地模拟溶洞顶板逐渐破坏直至垮塌的全过程。洞室周围首先出现应力集中现象,然后顶板出现破坏,随着破裂范围的增大,顶板最终出现垮塌从而导致整个溶洞破坏。本文中以洞室顶板发生完全垮塌破坏时的状态作为溶洞垮塌的判断依据。

1.3 确定溶洞临界垮塌埋深的二分深度折减法

使洞室达到临界垮塌破坏状态时的洞室埋深称为临界垮塌深度,当埋深小于此深度时,洞室不发生垮塌;当埋深大于此深度时,洞室发生垮塌破坏。借鉴强度折减法[18]计算边坡安全系数的思路,提出计算溶洞临界垮塌埋深的深度折减法,即通过不断调整溶洞埋深,达到临界破坏状态,此时对应的深度即为洞室临界垮塌深度。鉴于逐步求解临界垮塌深度计算工作量巨大,有时难以实现,因此采用二分法对问题进行优化处理,具体计算流程见图3。

计算过程中首先初始确定埋深的上、下限H1和H2,取两者的平均值H作为溶洞埋深进行数值分析。当溶洞不满足垮塌判据时,以H作为上限,H2仍作为下限重新进行数值分析直到溶洞满足垮塌判据,此时求得的溶洞垮塌深度并非临界垮塌深度,还须检验埋深的上、下限差值是否满足误差要求,若不满足要求则需继续对上、下限进行二分处理,直到满足误差要求,此时求得的上、下限的平均值就是溶洞的临界垮塌深度。

以上求解过程即为确定溶洞临界埋深的二分深度折减法,采用此方法不仅能控制误差，准确得到溶洞的临界垮塌深度,而且通过优化的二分法可以简化计算,减小计算工作量。

图3 临界垮塌深度求解流程Fig.3 Solving process of critical collapse depth

2 溶洞临界垮塌深度计算结果分析

2.1 不同洞型溶洞的变形破坏特征

计算考虑溶洞顶板厚度为5 m,洞跨为10 m,洞高为10 m,侧压力系数为0.62,按照图1建立数值分析模型,通过RFPA计算得到矩形溶洞、城门洞形溶洞和圆形溶洞的渐进垮塌破坏过程,结果如图4所示。

图4 不同洞型溶洞的渐进垮塌破坏过程Fig.4 Gradual collapse-failure process of different form caves

由图4可以看出,矩形溶洞洞室顶角的上部应力集中最为明显,逐渐产生局部损伤,并在顶板产生向下的挠曲。这些局部破坏均使顶板处的强度减小,承载能力下降,当洞室深度达到临界埋深时,顶板发生垮塌破坏;城门洞形溶洞从溶洞两侧的上部和拱顶的底脚开始出现局部破损并慢慢向上贯通,最终产生沿拱顶底脚向上的贯通破裂带,从而导致顶板发生垮塌。城门洞形溶洞和矩形溶洞围岩变形破坏特征均表现为顶板沿洞两侧的垂直洞壁直接塌陷,是一种竖向剪切破坏。

圆形溶洞在载荷作用下的变形破坏特征与矩形溶洞和城门洞形溶洞有较大差别,圆形溶洞的破坏模式表现为:顶板逐渐产生向下的挠曲,溶洞在顶板的变形过程中逐渐被压扁、压实,并在洞周产生较大范围的破损带。由于圆形溶洞没有垂直洞壁,导致其很难发生顶板沿溶洞两侧的竖向剪切破坏。

2.2 溶洞垮塌影响范围

图5为顶板厚度35 m、洞跨10 m的不同洞型溶洞的垮塌影响范围。由该图可以看出:①洞周应力集中区逐渐向外扩展,图中白色区域为剪应力集中区;②洞室的垮塌不仅会造成顶板的破裂与塌陷,也会对洞室围岩稳定造成影响,溶洞垮塌时的应力扩展范围即是溶洞垮塌影响范围。由图5可知，不同洞型溶洞垮塌影响范围为23～26 m,为2.3～2.6倍洞跨。根据上述方法可以计算出不同顶板厚度和洞跨时溶洞的垮塌影响范围,并绘制出不同洞型溶洞垮塌影响范围与顶板厚度的关系曲线和垮塌影响范围与洞跨的关系曲线(图6)。

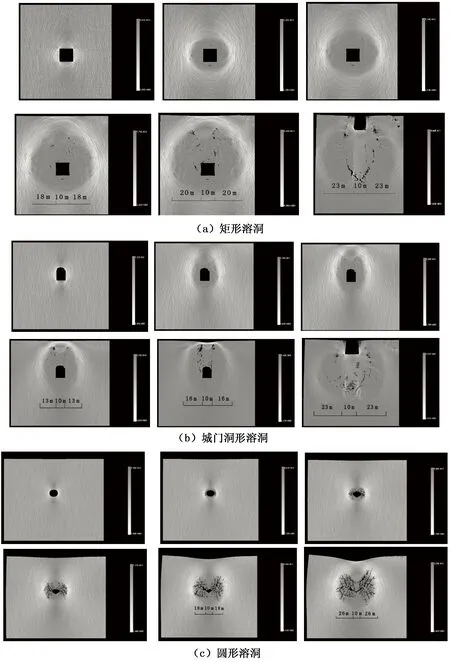
图5 不同洞型溶洞垮塌影响范围Fig.5 Collapse influence area of different form caves

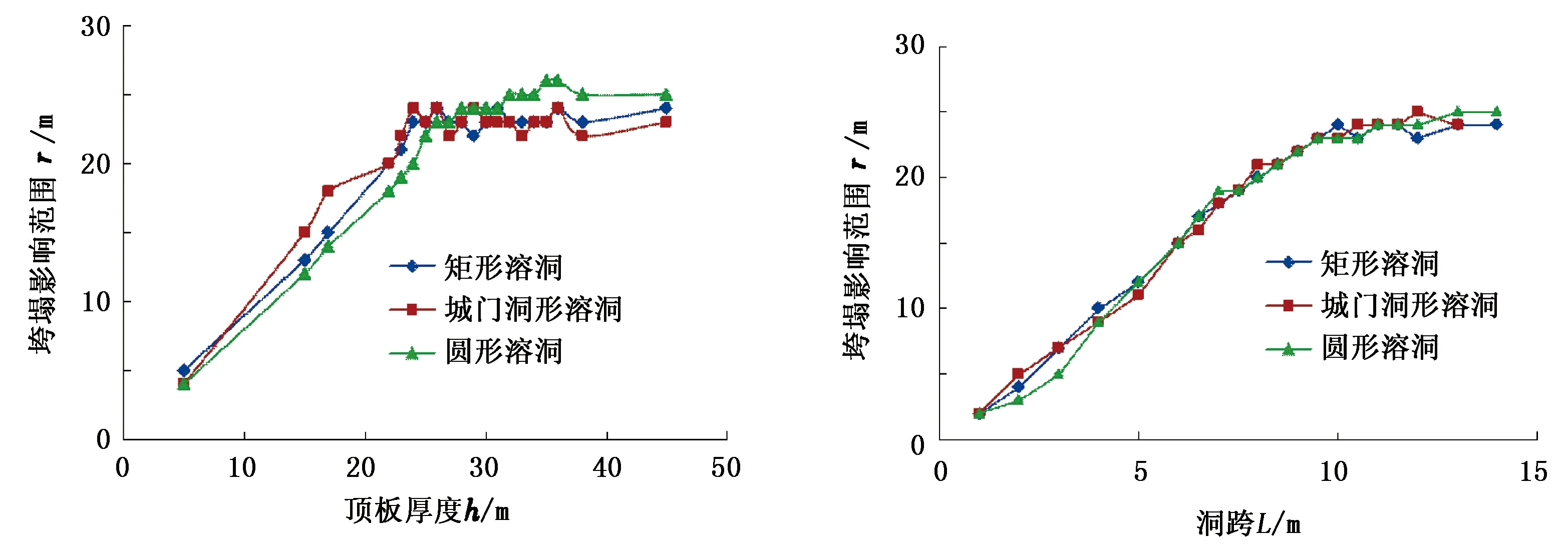
图6 垮塌影响范围随顶板厚度或洞跨的变化关系Fig.6 Relationship of collapse influence area with roof thickness and spans

由图6中可以看出:不同洞型溶洞垮塌影响范围随着顶板厚度的增加而增大,当顶板厚度大于2.5倍洞跨时,垮塌影响范围值趋于稳定;不同洞型溶洞垮塌影响范围随着洞跨的增加而增大,不同洞跨下溶洞垮塌影响范围为2.3～2.6倍洞跨;溶洞垮塌影响范围随顶板厚度和洞跨的增加而增大,最终趋于稳定,最大垮塌影响范围约为2.6倍洞跨。

2.3 单因素影响的溶洞垮塌深度计算结果

按照二分法确定溶洞临界垮塌埋深的计算方法,可得到不同顶板厚度、洞跨和侧压力系数下矩形溶洞、城门洞形溶洞和圆形溶洞的临界垮塌深度随顶板厚度、洞跨和侧压力系数的变化，结果如图7所示。

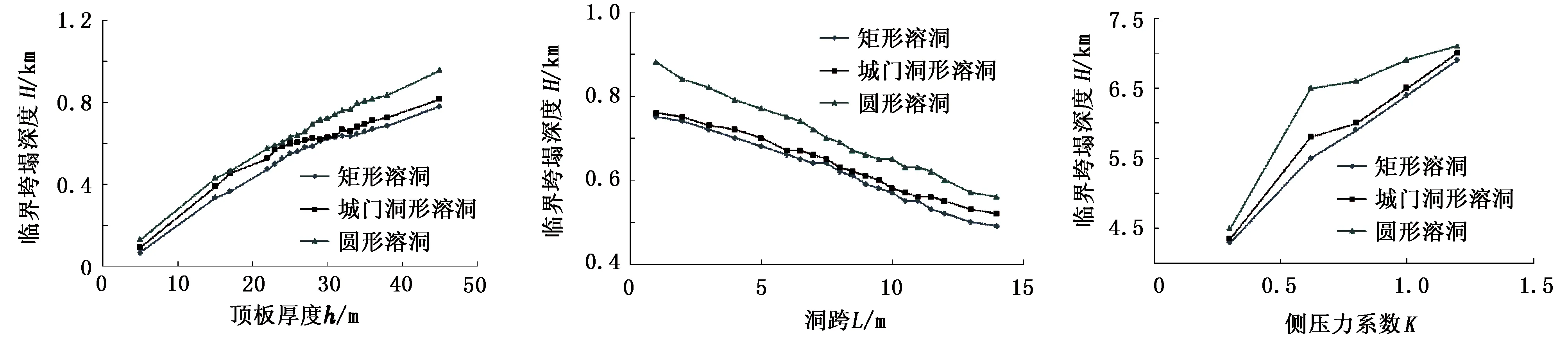
图7 临界垮塌深度与不同影响因素的关系Fig.7 Relationship between critical collapse depth and various factors

由图7可以看出:溶洞临界垮塌深度随顶板厚度和侧压力系数的增加而增大,即顶板厚度和侧压力系数越小,溶洞临界垮塌深度越小,溶洞越容易发生垮塌;溶洞临界垮塌深度随洞跨的增加而减小,即洞跨越大,溶洞临界垮塌深度越小,溶洞越容易发生垮塌;在洞跨、顶板厚度、侧压力系数相同时,矩形溶洞临界垮塌深度最小,城门洞形溶洞次之,圆形溶洞临界垮塌深度最大。在3种洞型中圆形溶洞最稳定,城门洞形溶洞次之,矩形溶洞稳定性最差。

溶洞临界垮塌深度与顶板厚度或洞跨或侧压力系数之间存在良好的线性关系(图7),以矩形溶洞为例,通过线性回归分析可得到溶洞垮塌深度随顶板厚度、洞跨和侧压力系数的变化关系表达式,

H=169.51h+853.58,R=0.948 8;

H=-325.22L+8 991.2,R=0.972 9;

H=3 478.1K+3 128.1,R=0.982 4.

由此可知，采用线性函数可以很好地描述溶洞临界垮塌深度随顶板厚度或洞跨或侧压力系数的变化关系。

2.4 溶洞垮塌的多因素敏感性

通过敏感性分析可以确定影响溶洞垮塌的主要因素及次要因素。根据本文中得到的单因素影响下溶洞临界垮塌深度与顶板厚度、洞跨、侧压力系数的关系式,可以分析溶洞垮塌对单因素的敏感性。但实际工程中溶洞垮塌是多因素影响作用产生的,须对这些参数进行无量纲化处理。

k=1,2,…,n.

(1)

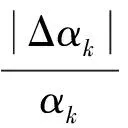
(2)

通过对Sk(αk)的比较,可以对影响溶洞垮塌的各因素的敏感性进行对比评价。以矩形溶洞为例分析溶洞垮塌对多因素的敏感性,由式(2)可以得到顶板厚度h、洞跨L和侧压力系数K的敏感度函数Sh(h)、SL(L)和Sk(K),敏感度曲线如图8所示。

图8 矩形溶洞垮塌对不同影响因素的敏感度曲线Fig.8 Sensitivity of rectangle cave collapse to different affecting factors

由图8可知,随着顶板厚度、洞跨、侧压力系数的不断增大,影响溶洞垮塌的敏感度因子不断增大;洞跨是影响溶洞垮塌的最敏感因素,其次为顶板厚度,侧压力系数对溶洞垮塌的影响最不敏感。

3 溶洞垮塌深度预测公式

由于溶洞受多种影响因素的共同作用,因此有必要同时考虑顶板厚度、洞跨和侧压力系数等多因素联合作用对溶洞垮塌深度的影响。临界垮塌深度H与顶板厚度h、洞跨L、侧压力系数K等单因素之间存在良好的线性函数关系,因此在建立多因素影响的临界垮塌深度预测模型时,可假设临界垮塌深度H与顶板厚度h、洞跨L和侧压力系数K之间也存在如下线性关系:

H=Ah+BL+CK+D.

(3)

式中,A、B、C和D为待定系数。

根据数值计算结果,通过多元线性回归优化求解,得矩形溶洞临界垮塌深度Hjx随顶板厚度h、洞跨L和侧压力系数K变化的预测公式为

Hjx=160h-369L+3 430.4K+2 923.8,R=0.917 2.

(4)

当侧压力系数取固定值0.62时,根据公式(4)可绘制出在不同洞跨L和顶板厚度h下的溶洞临界垮塌深度H的变化关系曲线,结果如图9、10所示。

由图9、10可以看出:洞跨不变时,溶洞垮塌深度随顶板厚度的增加而增大,顶板厚度越大,溶洞越不容易出现垮塌;顶板厚度不变时,溶洞垮塌深度随洞跨的增大而减小,洞跨越大,溶洞越容易产生垮塌。

采用类似的方法,得圆形溶洞和城门洞形溶洞的临界垮塌深度Hyx和Hcmd随顶板厚度h、洞跨L变化的预测公式为

Hyx=196.5h-270.3L+3 949.8,R=0.933 6;

Hcmd=154.66h-241.48L+4 263.8,R=0.942 5.

图10 不同顶板厚度下溶洞临界垮塌深度随洞跨的变化Fig.10 Variation of critical collapse depth with cave spans in different roof thicknesses

4 工程实例验证

为验证计算方法和溶洞垮塌深度预测公式的可靠性,选取文献[19]中塔河油田石灰岩洞穴发育的6口矩形溶洞进行验算。6口井的验算结果与原工程实测结果的对比见表1。

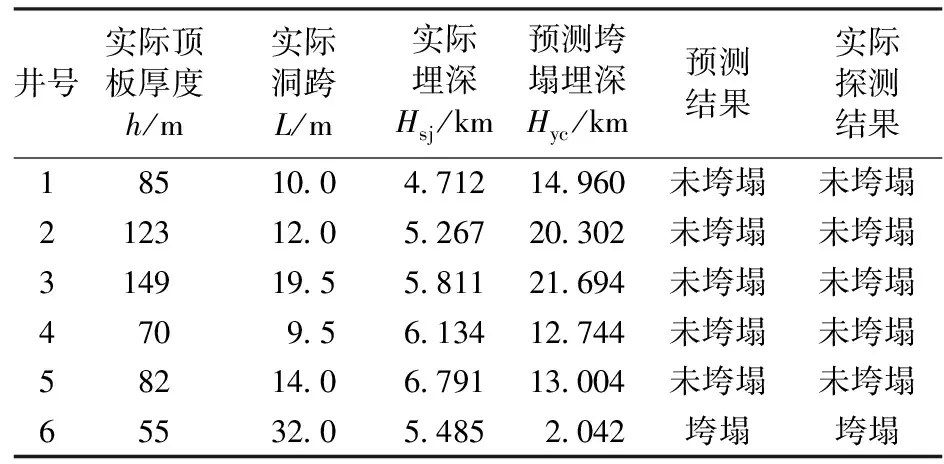
表1 验算结果与原型探测结果的对比

由表1可知:采用矩形溶洞临界垮塌深度预测公式得到的1至5号井的预测垮塌深度皆大于实际埋深,预测表明这5口井没有发生垮塌,与实际探测结果一致;而6号井的预测垮塌深度小于实际埋深,预测表明这口井发生垮塌,与实际探测结果一致。可见,采用本文中计算方法建立的缝洞型油藏溶洞的垮塌深度预测模型合理可靠。

5 结 论

(1)矩形和城门洞形溶洞为竖向剪切破坏,而圆形溶洞产生压实破坏;溶洞垮塌影响范围随顶板厚度和洞跨的增加而增大,最终趋于稳定,最大垮塌影响范围约为2.6倍洞跨;洞跨是影响溶洞垮塌的最敏感因素,其次为顶板厚度,侧压力系数对溶洞垮塌的影响最不敏感。

(2)溶洞的顶板厚度越大,溶洞越不容易出现垮塌。根据临界垮塌深度预测模型,针对不同埋深、不同洞跨溶洞,在石油钻探开发过程中,合理的顶板厚度应不小于临界垮塌顶板厚度。

(3)圆形溶洞最稳定,城门洞形溶洞次之,矩形溶洞稳定性最差。在石油开采过程中应尽量选择稳定性较高的圆形溶洞中进行开采,对城门洞形及矩形溶洞应制定专门的钻井方案。

[1] 康玉柱. 中国古生代碳酸盐岩古岩溶储集特征与油气分布[J]. 天然气工业,2008,28(6):1-12. KANG Yuzhu. Characteristics and distribution laws of paleokarst hydrocarbon reservoirs in palaeozoic carbonate formations in China[J]. Natural Gas Industry,2008,28(6):1-12.

[2] OKASHA T M,FUNK J J,AL-SHIWAISH A J. Evaluation of recovery efficiency and residual oil saturation of two distinct Arabian carbonate reservoirs [R].SCA 2003-37,1998.

[3] DONG Z,AIFEN L,JUN Y,et al. A single-phase fluid flow pattern in a kind of fractured-vuggy media[J]. Petroleum Science and Technology,2011,29(10):1030-1040.

[4] 李阳. 塔河油田碳酸盐岩缝洞型油藏开发理论及方法[J]. 石油学报,2013,34(1):115-121. LI Yang. The theory and method for development of carbonate fracture-cavity reservoirs in Tahe Oilfield [J]. Acta Petrolei Sinica, 2013,34(1):115-121.

[5] 杨坚,吴涛. 塔河油田碳酸盐岩缝洞型油气藏开发技术研究[J]. 石油天然气学报,2008,30(3):326-328. YANG Jian, WU Tao. Technique of reservoir development in carbonate fracture-vug reservoirs in Tahe Oilfield [J]. Journal of Oil and Gas Technology,2008,30(3):326-328.

[6] 张希明. 新疆塔河油田下奥陶统碳酸盐岩缝洞型油气藏特征[J]. 石油勘探与开发,2001,28(5):17-22. ZHANG Ximing. The characteristics of lower Ordovician fissure-vug carbonate oil and gas pools in Tahe oil field, Xinjiang. [J]. Petroleum Exploration and Development,2001,28(5):17-22.

[7] 李阳. 塔河油田奥陶系碳酸盐岩溶洞型储集体识别及定量表征[J]. 中国石油大学学报:自然科学版,2012,36(1):1-7. LI Yang. Ordovician carbonate fracture-cavity reservoirs identification and quantitative characterization in Tahe Oilfield [J]. Journal of China University of Petroleum(Edition of Natural Science),2012,36(1):1-7.

[8] 孟伟. 碳酸盐岩岩溶缝洞型油气藏勘探开发关键技术:以塔河油田为例[J]. 海相油气地质,2006,11(4):48-53. MENG Wei. The key technologies for exploration and development of fractured caverned karst reservoirs: a case of Tahe Oilfield, Tarim Basin. [J]. Marine Origin Petroleum Geology,2006,11(4):48-53.

[9] 邓洪军. 塔河油田碳酸盐岩储层放空漏失现象的研究与应用[J]. 中外能源,2007,12(5):47-52. DENG Hongjun. Study and application of blowing off the dropout phenomenon in carbonate rock reservoir of Tahe Oilfield [J]. Sino-Global Energy,2007,12(5):47-52.

[10] 牛玉静. 缝洞型碳酸盐岩油藏溶洞储集体岩溶塌陷结构特征研究[D].北京:中国地质大学能源学院,2012. NIU Yujing. Study on the structural and characteristics of karst collapse in fractured & cave carbonate reservoir [D]. Beijing:School of Energy Resources, China University of Geosciences, 2012.

[11] 张旭东,薛承瑾,张烨. 塔河油田托甫台地区岩石力学参数和地应力试验研究及其应用[J]. 石油天然气学报,2011,33(6):132-134,138. ZHANG Xudong, XUE Chengjin, ZHANG Ye. Research and application of rock mechanical parameters and in-situ stress in Tuofutai area of Tahe Oilfield[J]. Journal of Oil and Gas Technology, 2011,33(6):132-134,138.

[12] 罗强. 碳酸盐岩应力-应变关系与微结构分析[J]. 岩石力学与工程学报,2008,28(增1):2656-2660. LUO Qiang. Microstructure and stress-strain relationship of carbonate rock[J]. Chinese Journal of Rock Mechanics and Engineering, 2008,28(sup1):2656-2660.

[13] 周新桂,陈永峤,孙宝珊,等. 塔里木盆地北部地层岩石力学特征及地质学意义[J]. 石油勘探与开发,2002,29(5):8-12. ZHOU Xingui, CHEN Yongqiao, SUN Baoshan, et al. Rock mechanics characteristics in northern Tarim Basin and its geologic significance [J]. Petroleum Exploration and Development,2002,29(5):8-12.

[14] 王鹏昊,汤良杰,邱海峻,等. 塔里木盆地西北地区岩石力学格架及其地质意义[J]. 吉林大学学报:地球科学版,2012,42(增3):101-110. WANG Penghao, TANG Liangjie, QIU Haijun, et al. Rock mechanics framework and its geological implication in northwest Tarim Basin， China [J]. Journal of Jilin University(Earth Science Edition),2012,42(sup3):101-110.

[15] JAROT S, ARIFFIN S. Characterization, pressure, and temperature influence on the compressional and shearwave velocity in carbonate rock[J]. International Journal of Engineering and Technology, 2009,9(10): 80-93.

[16] 张敏思,朱万成,侯召松,等. 空区顶板安全厚度和临界跨度确定的数值模拟[J]. 采矿与安全工程学报,2012,29(4):543-548. ZHANG Minsi, ZHU Wancheng, HOU Zhaosong, et al. Numerical simulation for determining the safe roof thickness and critical goaf span[J]. Journal of Mining & Safety Engineering,2012,29(4):543-548.

[17] 贾蓬,唐春安,王述红. 巷道层状岩层顶板破坏机理[J]. 煤炭学报,2006,31(1):11-15. JIA Peng, TANG Chunan, WANG Shuhong. Destroy mechanism of tunnel with stratified roof [J]. Journal of China Coal Society,2006,31(1):11-15.

[18] 林杭,曹平,李江腾,等. 采空区临界安全顶板预测的厚度折减法[J]. 煤炭学报,2009,34(1):53-57. LIN Hang, CAO Ping, LI Jiangteng, et al. The thickness reduction method in forecasting the critical safety roof thickness of gob area [J].Journal of China Coal Society,2009,34(1):53-57.

[19] 郑兴平,沈安江,寿建峰,等. 埋藏岩溶洞穴垮塌深度定量图版及其在碳酸盐岩缝洞型储层地质评价预测中的意义[J]. 海相油气地质,2009,14(4):55-59. ZHENG Xingping, SHEN Anjiang, SHOU Jianfeng, et al. A Quantitative plate of collapsed karst cave depth and its application in geological prediction and evaluation of carbonate reservoir [J]. Marine Origin Petroleum Geology,2009,14(4):55-59.

(编辑 李志芬)

A prediction model for collapse of karst caves in fractured-vuggy oil reservoirs and its application

WANG Chao1, ZHANG Qiangyong1, LIU Zhongchun2, YUAN Shengbo1, ZHANG Xutao1,3, WANG Youfa1

(1.GeotechnicalandStructuralEngineeringResearchCenterofShandongUniversity,Jinan250061,China;2.SINOPECResearchInstituteofPetroleumExplorationandProduction,Beijing100083,China;3.SchoolofArchitectureandEngineering,LiaochengUniversity,Liaocheng252059,China)

The karstic caves in fractured-vuggy oil reservoirs may collapse during drilling. A model was proposed to predict the critical burial depth of the caves, which may cause cave collapse during well-drilling operations. The model was based on a method of depth dichotomy reduction and the data from the fractured-vuggy reservoirs in Tahe Oilfield Northwest China were used. Various factors that may affect the collapse of the cave were analyzed. A correlation for predicting the critical collapse depth was given through a multivariate regression analysis method, considering the influence of the coping thickness and span of the caves, and the lateral pressure coefficient. A case study for different caves in Tahe Oilfield was conducted. The analysis results show that the collapse of rectangle and horseshoe-shaped caves can be attributed to vertical shear failure, while the collapse of circular caves can be due to compaction failure. The influence area of the collapse increases with caves coping thickness and span, the largest influence area can be extended to 2.6 times of the cave span, which is the most sensitive factor to cave collapse. The lateral pressure coefficient is a less sensitive factor in comparison with the caves coping thickness and span. The circular caves are more stable than the horseshoe-shaped caves, and the rectangle caves are most vulnerable for collapse. The predicted results agree well with oilfield data.3

fracture-vuggy oil reservoir; critical collapse depth; method of depth dichotomy reduction; cave collapse mode; collapse depth prediction model

2014-05-06

国家自然科学基金项目(41172268，51279093)；国家科技重大专项(2011ZX05014)

王超(1989-)，男，博士研究生，主要从事岩土工程方面的研究。E-mail：ws8727200@163.com。

1673-5005(2015)01-0103-08

10.3969/j.issn.1673-5005.2015.01.015

TE 344

A

王超,张强勇,刘中春,等. 缝洞型油藏溶洞临界垮塌深度预测模型及其应用[J].中国石油大学学报:自然科学版,2015,39(1):103-110.WANG Chao, ZHANG Qiangyong, LIU Zhongchun, et al. A prediction model for collapse of karst caves in fractured-vuggy oil reservoirs and its application[J].Journal of China University of Petroleum(Edition of Natural Science),2015,39(1):103-110.