一基于高阶稀疏Radon变换的预测多次波自适应相减方法

薛亚茹, 杨 静, 钱步仁

(中国石油大学地球物理与信息工程学院,北京 102249)

一基于高阶稀疏Radon变换的预测多次波自适应相减方法

薛亚茹, 杨 静, 钱步仁

(中国石油大学地球物理与信息工程学院,北京 102249)

利用高分辨率稀疏Radon变换和正交变换两种原子构成过完备的信号重构空间,使得地震信号在此高阶高分辨率稀疏Radon变换域中能够被稀疏表示;结合基于过完备字典的信号稀疏表示,提出高分辨率稀疏Radon变换和正交多项式变换结合的高阶稀疏Radon变换(HOSRT)。所提方法通过将地震数据和预测多次波变换到高阶稀疏Radon空间,用完备的高阶稀疏Radon变换原子稀疏表示,并在该域进行自适应相减,能够有效分离一次波和多次波;而且由于构造的完备空间克服了正交性的问题,压制过程中降低了对一次波的损伤。对合成地震记录和实际资料的处理结果表明该方法能够提高多次波的压制效果,同时还可以较好地保留一次波振幅AVO(振幅随偏移别距的变化)特性。关键词:Radon变换; 正交多项式变换; 过完备字典; 自适应相减; AVO(振幅随偏移距的变化)

压制多次波的方法有预测相减法和滤波法两大类[1]。基于波动理论的预测相减法(SRME)有波场外推法、反馈迭代法和逆散射级数法[2]。Verschuur等利用基于一次波能量最小化的方法实现多次波自适应相减[3],会损伤一次波的AVO(振幅随偏移距的变化)信息。一些学者提出了自适应相减方法的约束条件,例如基于模式的自适应相减技术[4],利用多次波和一次波在变换域差异的自适应相减技术[5],非平稳回归自适应相减技术[6],在二阶统计量的基础上完成多次波压制;如L1范数的自适应相减算法,假设相减后数据的L1范数模最小[7,8];考虑了实际地震数据一次波和多次波的非正交性的基于独立分量技术的自适应相减方法[9];李钟晓等[10]和Li等[11]提出的基于卷积混合盲分离方法,亦不需要一次波和多次波正交假设。滤波法中Radon变换是目前压制多次波常用且有效的方法之一[12]。Thorson提出一种基于最小熵的高分辨率Radon变换[13];Sacchi提出基于Bayes理论的随机反演方法[14]。为提高Radon变换分辨率,许多学者提出了各种改进形式的高分辨率Radon变换[15]。Wang等[16]提出速度子空间的思想,通过贪婪算法实现稀疏Radon变换,提高了计算速度。Wang等[12]将地震数据分解为常规Radon变换和一阶Radon变换,改善了一次波AVO特性。在Radon 域切除多次波也会影响一次波的振幅。为了解决这一问题,Wang等[17]利用Radon参数作为滤波器的模板,在时间域实现自适应相减;石颖等[18]将预测多次波在Radon域的投影作为Radon域非线性滤波器设计参数做自适应相减。上述两种方法采用在Radon域实现多次波的非线性滤波,最终仍是在时间域做多次波自适应相减,无法避免两波重叠处对一次波有所损伤的问题。有的学者提出在Radon域直接自适应相减[19],Li等[20-21]提出在Radon域用匹配滤波器进行一次波和多次波分离,但这种方法仍会面临Radon变换不保幅的问题。针对Radon变换非正交问题及时间域自适应相减损伤一次波的问题,笔者提出一种基于高阶稀疏Radon变换(HOSRT)的预测多次波自适应相减方法来压制多次波,将常规Radon变换延拓至高阶,结合过完备字典下信号的稀疏表示在该域进行自适应相减。

1 高阶Radon变换

1.1 Radon变换的基本原理

Radon变换根据积分路径的不同可以分为线性、抛物和双曲Radon变换,在此处以抛物Radon变换为例给出变换方法,该方法可以推广至其他类型的Radon变换。

抛物Radon变换模型方程[22]为

(1)

该模型表示地震数据可以被表示成一系列抛物路径的恒等振幅同相轴的线性组合。m(τ,q)为每一函数的加权系数。当同相轴振幅发生变化时,会引起q参数的扩散,导致分辨率降低。稀疏Radon变换的基本原理是将信号的Radon参数与反演矩阵结合,提高Radon域能量较大参数的反演权重,通过多次迭代,Radon变换将聚焦在某些参数区域,较好地分离了各参数。然而由于稀疏Radon变换是由常振幅的同相轴构成,稀疏的Radon参数反变换到t-x域后会造成同相轴AVO信息的丢失,因此在利用稀疏Radon变换处理数据时需要权衡Radon分辨率与t-x域数据保幅。

1.2 高阶Radon变换

高阶Radon变换考虑了振幅随炮检距变化的特性,可以较好地保留地震数据的AVO现象,在地震数据重建中得到较好的应用[23]。本文中从基于过完备词典的信号稀疏表示角度重新阐述高阶Radon变换的基本原理。

常见的信号分解变换是在完备的正交基函数上进行的,如Fourier变换、小波变换,它们对给定信号的表示形式唯一且对信号特性有一定的要求。将这些表现形式拓展,找到能够将信号完全或者近似表示的一组原子,即可组成一个过完备字典(字典原子数目大于每个原子的维数),并在这个字典上能够使用一种稀疏的表示来逼近原始信号。利用过完备词典对信号进行稀疏表示[24]可以有效提高信号在变换域的分辨率,但须解决两个关键问题:一是如何构造过完备词典,二是如何寻找稀疏解。

常规Radon变换主要考虑了地震同相轴路径的变化,而没有考虑振幅变化。采用常数振幅同相轴作为地震数据分解的基函数,这样的基函数与实际同相轴振幅随炮检距变化的特点不一致,所以导致Radon域参数的扩散,即分辨率的降低。地震振幅随炮检距变化可以用多项式表示[25],正交多项式变换[26]将地震AVO特性用较少的几个多项式系数表征，因此引入描述振幅变化的变换空间,与积分路径空间共同构成过完备空间,在过完备字典中加入表示振幅随炮检距变化的正交多项式,将Radon变换与正交多项式变换结合构成高阶Radon变换。

设{pj(x),j=0,1,…，N}是由N+1个偏移距坐标x确定的单位正交多项式集,pj(x)是j阶代数多项式,满足pi(x)pj(x)=δij。地震数据d(t,x)在某时刻的振幅变化可以用正交多项式拟合[28],即

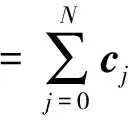
(2)

式中,cj(t)为t时刻振幅随偏移距变化的j阶正交多项式的分解系数,称之为正交多项式系数谱。公式(2)将地震数据分解为一系列多项式的线性组合,符合地震数据AVO变化的特点。

Radon变换描述了积分路径的变化,正交多项式包括了振幅的变化,这两个字典互不相干,构成新的过完备字典,可以将地震数据分解为一系列沿积分路径振幅变化的同相轴叠加。将式(1)和(2)结合可以得到高阶Radon变换的离散表示

(3)

由于{pj(x),j=0,1,…,N}是正交多项式多项式集,式(3)两侧同时乘以pj(x)可以得到高阶Radon变换的共轭解

(4)

该变换将地震数据分解为各阶Radon剖面,其中m0(τ,q)表示沿积分路径的叠加结果,与常规Radon变换一致;m1(τ,q)表示沿积分路径同相轴振幅的斜率变化特征;m2(τ,q)表示同相轴振幅的曲率变换特征;更高阶的Radon变换描述了同相轴振幅的变换细节,甚至包含了噪声。通常采用二阶Radon变换,m0(τ,q)、m1(τ,q)、m2(τ,q)也是AVO反演的重要参数。

1.3 高阶稀疏Radon变换

上述高阶Radon变换用矩阵形式可以表示为

(5)

式中,L0、L1、L2分别表示叠加、梯度和曲率算子。与常规Radon变换相比,将变换算子由零阶L0扩展到了高阶算子L0、L1、L2,因此命名为高阶Radon变换。高阶Radon变换的稀疏模型为

(6)

式(6)是一个NP问题,通常考虑近似解法,常用方法有匹配追踪算法(match pursuit,MP)[27]和基追踪算法(basis pursuit, BP)[27]。MP 算法采用了贪心的思想,每次选择一组最优的原子使得其与前一步的残差内积达到最大。Wang利用该方法实现快速的稀疏Radon变换[16]。该方法关键是如何选择最优的原子组。Wang将Radon变换的共轭解作为原子选择的初始值,从中选取幅度较大的参数作为下一步反演的参数空间(即原子)。但是当考虑到AVO特性时,振幅不一定能够反映同相轴的能量。例如同相轴各道振幅叠加为零,在Radon剖面上就无法识别出来,因此选用同相轴能量作为同相轴识别的标志比振幅阈值要稳定。

由于高阶Radon 变换是Radon变换与正交多项式变换结合,根据Pasval定理[28]可以得到Radon域能量分布

(7)

该能量表示了不同τ时间沿不同曲率方向同相轴的能量分布。利用该阈值作为变换子空间的选择依据,通过迭代方法选出反演的最优原子。高阶稀疏Radon变换的实现方法可以分为以下步骤。

(1)用原始数据d作为初始化残差数据 dresi,初始化Radon参数m为零;

(2)重复以下步骤直至满足停止条件:

②用公式(7)计算Radon能量分布,据局部极大值选取Radon子空间 Si,

③利用共轭梯度法最小化代价函数

(8)

式中,mi是在上述子空间Si下的最小二乘解。由于子空间远远小于原有的空间参数,因此计算速度会大大提高。

④更新参数m=m+mi, 残差数据dresi=dresi-Lmi。

最后所有的子空间Si构成了高阶稀疏Radon变换。

2 高阶稀疏Radon变换的多次波自适应相减

利用Radon变换压制多次波通常要求一次波和多次波有足够大的剩余时差差别,在很多情况下该假设无法满足,多次波的压制性能和保护一次波振幅的性能下降。基于波动方程的多次波预测相减可以处理较复杂的地质情况,在很多情况下预测多次波和一次波是相交的,不满足正交性,通过自适应相减后,损伤了一次波能量。将两者方法结合,把地震数据和预测多次波均变换到高阶Radon空间,在t-x空间相交的一次波和多次波在Radon空间得到了适当的分离,经自适应相减后可以减小对一次波的损伤。

假设地震数据和预测多次波的高阶Radon变换为D和M,滤波器为f,在Radon空间一次波和多次波得到较好分离,因此期望相减后剩余能量最小,也就是多次波得到最大程度的压制,即

(9)

其中*表示褶积算子,易得滤波算子

f=(MTM+λI)-1MTD.

(10)

式中,MTM为预测多次波模型的自相关;MTD为预测多次波模型数据与输入地震数据的互相关;λI为阻尼约束因子,增加多次波模型的自相关逆矩阵求解的稳定性。

经过上述自适应相减后,原始地震数据中只保留了一次波能量,经过高阶Radon反变换,一次波能量得到较好的保持。

3 实例分析

高阶稀疏Radon变换预测多次波压制主要利用了基于过完备字典稀疏信号的高阶稀疏Radon变换的保幅和高分辨率的特性。图1(a)是某一合成地震数据记录,道间距为25 m,采样点为150,采样间隔为2 ms,包含三种类型AVO:第一个同相轴振幅随炮检距增长,其振幅均值、梯度和曲率分别为0.6,0.05,-0.1;第二个同相轴振幅首先衰减,经过零点后又开始增长,其振幅均值、梯度和曲率分别为0.1,-0.7, 0.1;第三个同相轴振幅随炮检距衰减,其振幅均值、梯度和曲率分别为0.6,-0.2,0.1。图2(a)是其稀疏Radon变换结果,可以看到第二个同相轴由于振幅均值较小,在Radon参数识别时产生误差,导致分辨率降低;其反变换数据及其误差如图1(b)和(c)所示,可以发现利用稀疏Radon变换重构的第二个同相轴远偏移距偏离了真实路径,产生较大的误差;同时重构数据在近偏移距也存在较大误差。高阶稀疏Radon剖面道数为50,变换的结果m0(τ,q)、m1(τ,q)、m2(τ,q)如图2(b)、(c)和(d)所示,其分辨率高于常规Radon变换的分辨率,并且各阶Radon剖面真实反映了各个同相轴振幅变化的三个参数,保留了同相轴的AVO特性;其反变换结果和误差剖面如图1(d)和(e)所示,可以看到该方法较好地重构了原数据。

图1 Radon变换与高阶Radon变换重构数据对比Fig.1 Reconstruction comparison between Radon transform (RT) and HOSRT

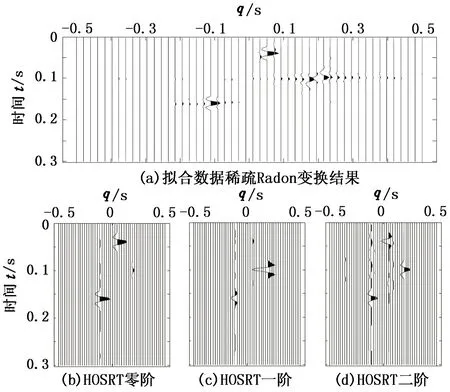
图2 Radon变换与高阶Radon变换对比Fig.2 Resolution comparison of RT and HOSRT

第二个模型用以说明高阶Radon变换多次波压制效果。图3(a)所示为某同相轴相交的地震记录模型,采样间隔为2 ms,其水平同相轴表示动校正一次波模型,弯曲同相轴表示多次波。假设多次波已知,都采用基于一次波能量最小化的单道相减方法,时间域自适应相减结果如图3(b)所示,可以看到相交部分的一次波由于与多次波不满足正交关系也被压制。GRT(greedy Radon transform)自适应压制的结果如图3(c)所示,可以看到多次波有些残留;误差剖面如图3(e)所示,在近偏移距一次波振幅误差较大,这一点对AVO反演和叠加成像不利。HOSRT压制多次波的结果及误差剖面如图3(d)和(f)所示,一次波振幅随炮检距衰减的特性明显显示出来,在误差剖面上基本没有残留。此例中GRT和HOSRT自适应相减数据的窗口长度一致,均为50,而匹配滤波器阶数为10阶。

图4是利用理想多次波作为预测多次波,自适应相减前后Radon剖面的对比。图4(a)是GRT自适应相减结果的变换域剖面,利用HOSRT进行自适应相减的结果如图4(b)所示,可以看到前者在近偏移距处多次波仍有残留;由于一次波和多次被基本分离,基于HOSRT的多次波自适应相减基本没有影响一次波参数,图4(c)、(d)亦证明了这一点。 原始数据的变换域零阶如图4(c)所示,而图4(d)中为HOSRT自适应相减结果的变换域零阶,可看出在压制干净多次波的同时,HOSRT变换对一次波的AVO保护得很好。

图3 多次波压制效果对比Fig.3 Comparison of demultiple results

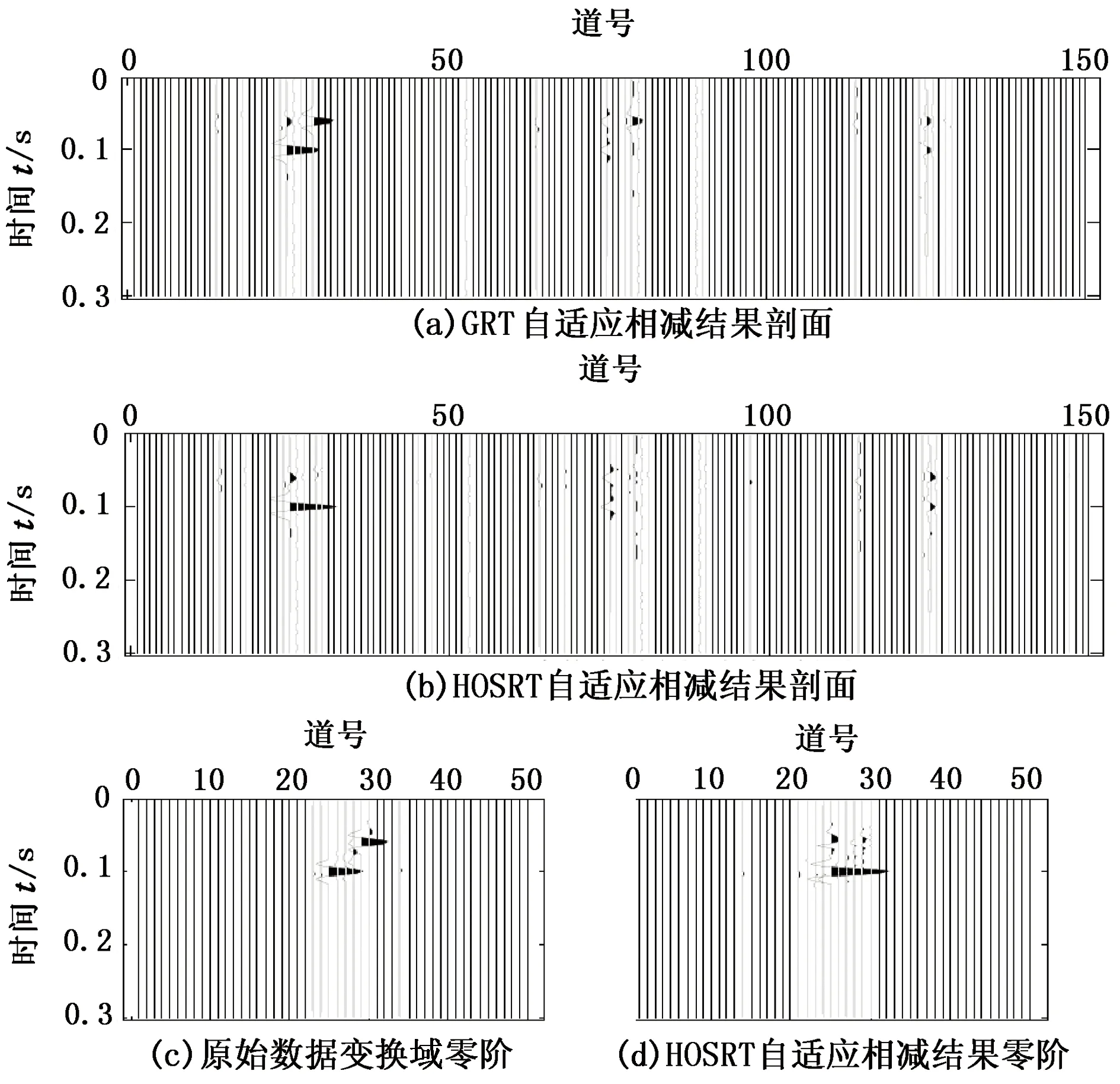
图4 自适应相减Radon剖面对比Fig.4 Comparison of Radon parameters

为进一步衡量HOSRT保留一次波振幅特性的能力,定义以下三个衡量参数:零炮检距道能量相对误差ee(relative error of energy);一次波振幅均值相对误差ea(relative error of amplitude average); 一次波振幅梯度相对误差eg(relative error of amplitude gradient)。定义Ptrue表示真实一次波零炮检距数据,P表示去多次波后零炮检距结果,Atrue和A分别表示一次波真实振幅均值和去多次波后的振幅均值;Gtrue和G分别表示一次波真实振幅梯度和去多次波后的振幅梯度,则上述三个参数定义分别为

(11)

(12)

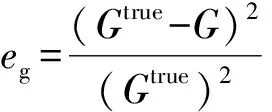
(13)

假定Δτ0表示一次波与多次波在零偏移距旅行时差,Δτmax表示最远偏移距旅行时差,图5反映了一次波在一定Δτ0的情况下,随着多次波远偏移距的变化各参数的变化曲线。可以看出,HOSRT较好地保留了一次波的能量及振幅变化特性,该优势有利于AVO参数的反演。

图6所示为某实际地震数据和预测多次波在时间域和高阶Radon域自适应相减的对比。图6(a)为一个实际单炮180道的地震数据剖面,每道采样1 500点;图6(b)为基于波动方程预测(SRME)方法得到的多次波;图6(c)为在时间域中利用自适应相减法去除多次波的结果,红圈所在的局部放大为图6(e);图6(d)为利用本文中介绍的基于高阶Radon变换的自适应相减法去除多次波结果,红圈所在的局部放大为图6(f)。如图中所示,高阶Radon变换预测多次波自适应相减方法能够更有效地压制多次波,同时保持有效波的幅度变化信息。该例中所用自适应滤波器皆为10阶,开窗长度为10。

图5 GRT和HOSRT自适应相减相对误差比较Fig.5 Relative error comparison between GRT and HOSRT

图6 两种方法压制实际数据中多次波结果对比Fig.6 Comparison of marine data demultiple results

4 结束语

通过结合正交多项式变换和高分辨率Radon变换,构成高阶稀疏Radon变换。此方法中两种变换原子构成的过完备字典可以对地震信号进行稀疏表示,从而提高变换域的分辨率;同时将自适应相减过程从时间域平移到高阶稀疏Radon域中,克服了时间域压制多次波损伤一次波振幅的问题,在完备且稀疏的HOSRT中进行预测多次波的自适应相减,既可以改善对多次波的压制效果,提高降噪水平,又可以保护一次波振幅变化不受损伤,保存更多的一次波AVO信息。

[1] WEGLEIN A B. Multiple attenuation: an overview of recent advances and the road ahead [J]. The Leading Edge, 1999,18(1):40-44.

[2] VERSCHUUR D J. Seismic multiple removal techniques: past, present and future [M]. Houten: EAGE Publications, 2006:16-17.

[3] VERSCHUUR D J, BERKHOUT A J, WAPENARR P A. Adaptive surface related multiple elimination [J]. Geophysics, 1992,57(9):1166-1177.

[4] GUITTON A. Multiple attenuation in complex geology with a pattern-based approach [J]. Geophysics, 2005,70(4):V97-107.

[5] HERMANN F J, WANG D, VERSCHUUR D J. Adaptive curvelet-domain primary-multiple separation [J]. Geophysics,2008,73(3):A17-21.

[6] FOMEL S. Adaptive multiple attenuation using regularized non-stationary regression [J]. Geophysics,2009,74(1):V25-33.

[7] 李学聪,刘伊克,常旭,等.均衡多道1范数匹配多次波衰减的方法与应用研究[J].地球物理学报,2010,53(4):963-973. LI Xuecong, LIU Yike, CHANG Xu, et al. The adaptive subtraction of multiple using the equipoise multichannel L1-morm matching [J]. Chinese Journal of Geopysics, 2010,53(4):963-973.

[8] GUITTON A, VERSCHUUR D J. Adaptive subtraction of multiple using the L1-norm [J]. Geophysical Prospecting, 2004,52(1):27-38.

[9] LU W K, LIU L. Adaptive multiple subtraction based on constrained independent component analysis [J]. Geophysics, 2009,74(1):V1-7.

[10] 李钟晓, 陆文凯, 王季, 等. 基于多道卷积信号盲分离的多次波自适应相减方法 [J]. 地球物理学报, 2012,55(4):1325-1334. LI Zhongxiao, LU Wenkai, WANG Ji, et al. Adaptive multiple subtraction based on multi-traces convolutional signal blind separation [J]. Chinese Journal of Geopysics, 2012,55(4):1325-1334.

[11] LI Zhongxiao, LU Wenkai. Adaptive multiple subtraction based on 3D blind separation of convolved mixtures [J]. Geophysics, 2013,78(6):V251-V266.

[12] WANG B, SACCHI M, YIN X. AVO-preserving sparse parabolic Radon transform: proceedings of the 73rd EAGE Conference and Exhibition, A033, Houten,The Netherlands, May-23, 2011 [C]. Cambridge: Cambridge University Press, c2011.

[13] THORSON R, CLAERBOUT J. Velocity-stack and slant-stack stochastic inversion [J]. Geophysics, 1985,50:2727-2741.[14] SACCHI M, ULRYCH T. High-resolution velocity gathers and offset space reconstruction [J]. Geophysics, 1995,60(4):1169-1177.

[15] TRAD T, ULRYCH T, SACCHI M. Latest views of the sparse Radon transform [J]. Geophysics,2003,68(1):386-399.

[16] WANG J F, NG M, PERZ M. Seismic data interpolation by greedy local Radon Transform [J]. Geophysics, 2010,75(6):225-234.

[17] WANG Y. Multiple attenuation: coping with the spatial truncation effect in the Radon transform domain [J]. Geophysical Prospecting, 2003,51:75-87.

[18] 石颖,王维红.基于波动方程预测和双曲Radon 变换联合压制表面多次波[J].地球物理学报,2012,55(9):3115-3125. SHI Ying, WANG Weihong. Surface-related multiple suppression approach by combining wave equation prediction and hyperbolic Radon transform [J]. Chinese Journal of Geophysics, 2012,55(9):3115-3125.

[19] 马继涛,姚逢昌,陈小宏,等.倾角分解多次波自适应相减方法研究[J].石油物探,2012,51(4):356-361. MA Jitao, YAO Fengchang, CHEN Xiaohong, et al. Multiple self-adaptive subtraction based on dip decomposition[J]. Geophysical Prospecting for Petroleum, 2012,51(4):356-361.

[20] LI Z X, LU W K. Hybrid demultiple method in the Radon domain: proceedings of The 75rd EAGE Conference and Exhibition, Tu14 07,London,June-10,2013[C]. Cambridge: Cambridge University Press, c2013.

[21] LI Zhongxiao, LU Wenkai. Demultiple strategy combining Radon filtering and Radon domain adaptive multiple subtraction [J]. Journal of Applied Geophysics, 2014,103:1-11.

[22] HAMPSON D. Inverse velocity stacking for multiple elimination[J]. Journal of Canada Social Exploration Geophysics, 1986,22:44-55.[23] XUE Yaru,MA Jitao and CHEN Xiaohong. AVO-Preserving Data Reconstruction based on High-Order Sparse Radon Transform: Proceedings of The 75th EAGE Conference and Exhibition, Th P04 11, London, June-10, 2013[C]. Cambridge: Cambridge University Press, c2013.

[24] MALLA G, ZHANG Z F. Matching pursuit with time-frequency dictionaries[J]. IEEE Transaction on Signal Processing,1993,41(12):3397-3415.

[25] URSIN B, DAHL T. Least-square estimation of reflectivity polynomials: 60th SEG Meeting, Expanded Abstracs[C]. San Francisco, California: Society of Exploration Geophysicists, c1990:1069-1071.

[26] JOHANSEN T A, BRULAN L, LUTRO J. Tracking the AVO by using orthogonal polynomials [J]. Geophysical Prospecting, 1995,43:245-261.

[27] CHEN S, DONOHO D, SAUNDERS M. Atomic decomposition by basis pursuit [J]. SIAM Review,2001,43(1):129-159.

[28] MACIEJ BORODZIK, HENRYK ZOLADEK. The pascal theorem and some its generalizations [J].Journal of the Juliusz Schauder Center,2002,19:77-90.

(编辑 修荣荣)

Multiples prediction and adaptive subtraction with high-order sparse Radon transform

XUE Yaru, YANG Jing, QIAN Buren

(CollegeofGeophysicsandInformationEngineeringinChinaUniversityofPetroleum,Beijing102249,China)

An adaptive subtraction in high-order sparse Radon domain for multiple-elimination is proposed. Subtraction in time domain can damage primary while it is overlapped with multiples. Radon transform is not an orthogonal transformation; its inversion will loss data trivial. For primary-preservation, the high-resolution sparse Radon transform is incorporated with orthogonal polynomial transformation and sparse representation by an overcomplete dictionary, thus a high-order sparse Radon transform is achieved. The high-order sparse Radon transform not only keeps primary amplitude but improves the resolution of multiple elimination. The adaptive subtraction in high-order sparse Radon domain will decrease the damage to the primaries. The experiments with synthetic data and field data show good performances in multiple elimination and AVO(amplitude versus offset)-preservation.

Radon transform;orthogonal polynomial transform; overcomplete dictionary; adaptive subtraction; AVO(amplitude versus offset)

2014-03-21

国家自然科学基金项目(41204095)

薛亚茹(1972-)， 女，副教授，博士，从事信号处理方面的研究。E-mail：xueyaru@cup.edu.cn。

1673-5005(2015)01-0043-07

10.3969/j.issn.1673-5005.2015.01.006

TE 132

A

薛亚茹,杨静,钱步仁. 基于高阶稀疏Radon变换的预测多次波自适应相减方法[J].中国石油大学学报:自然科学版,2015,39(1):43-49.

XUE Yaru, YANG Jing, QIAN Buren. Multiples prediction and adaptive subtraction with high-order sparse Radon transform [J].Journal of China University of Petroleum(Edition of Natural Science),2015,39(1):43-49.