美国高校商业学科数学教学的现状及发展趋势

钟建媛，鲁 斌

（美国加利福尼亚州州立大学 萨克拉门托分校 数学统计系，美国）

美国高校商业学科数学教学的现状及发展趋势

钟建媛，鲁 斌

（美国加利福尼亚州州立大学 萨克拉门托分校 数学统计系，美国）

数学课是美国高校商学院学生的必修课．对美国大学中为商业学科而开设的数学课程进行介绍，对几种有代表性的商业数学及其课程内容做出分析和比较，并且列举具有代表性的实际应用例题来突出商业数学课程的特点，并对当前科学技术在商业数学教学中的运用做出讨论．

商业数学；大学数学；微积分；课程内容

1 引 言

在美国大学中，商学院一般是一个较大的学院．商学院通常设有会计、经济、金融、市场、管理等不同的专业，拥有很多的专业学生．虽然商学院的学生属于不同的系，读不同的专业，但是每个专业都有对普通教育课程（General Education或GE）学分的要求．所要求的数学课就是这样的GE课程之一，是商学院学生的一门必修课．商学院的学生在通过这门课之前只属于学院“非正式”学生（pre-majors)，只有修完并考试通过这门课之后，才能正式成为商学院的学生而进入专业学习．可以说，为商学院开设的数学课对许多读商科的学生是一个“门槛”，就像微积分（高等数学）是工科学生进入专业前必须通过的课程．因此，如何提高商业数学课的教学质量，让更多的学生顺利通过此课程，尽早进入专业学习，常常是学校数学系和商学院共同关心的一个问题．

在美国大学中，商学院学生所修的数学课名通常称为商业数学，商业微积分，应用微积分等．有的学校开设有限数学，还有些综合微积分和有限数学内容合并成为一门课．这些课程都有一个显著的特点，就是通过从商业学科中的实例来强调数学在商业学科中的应用，例如最优值问题，边缘分析等．

这些课程的学习时间一般都是一学期（3～4学分），而且学生在正式修这些课程之前必须满足修课的前提要求（prerequisites）：比如学生在此之前是否修过有关代数的课程（如大学代数课程），要通过“诊断”考试等，其目的是评估选课的学生是否具有足够的预备知识，以最大程度上确保学生能够通过这门课程．

尽管为商学学科而设置的数学课程名称比较多，但在内容上大致可以分为几类．在下文中将较详细地介绍其内容并列举几个实例．

2 课程内容

通常不同大学开设有不同商业数学课程，但是传统上这些课程可分成：商业微积分和应用数学及其在管理和商业科学中的应用．在以下的讨论中，可以了解这些课程的内容及包含在课程中商业、经济学科中所出现的应用例子．从这些例题中可以看出该课程具有数学在商业科学应用的独特之处，进而突出该课程是为商学院的学生专门设置而与其它数学课程不同．

2.1 商业微积分课程[3～4]

该课程内容包括传统一元微积分内容 （但不涉及三角函数）：函数与图像、极限、导数、导数及应用、极值问题、积分及应用．针对商学院的学生，课程中含有许多微积分在商业科学中的应用．例如导数中的边缘分析和弹性需求应用，指数增长及衰减模型，等等．下面的例子就是一个积分在商业中的应用，即用定积分来计算消费者的顺差额和供应商的顺差额．

例1 已知某家生产变速自行车工厂的需求函数是：

这里p代表自行车的单价，x是所需求的数量（单位为千辆）．另外这种自行车的供应函数是：

这里p代表自行车的单价，x是厂家供给市场的数量（单位为千辆）．如果市场的价格是市场的均衡价格，求消费者顺差额和制造厂家的顺差额．

例题2是导数在边缘分析中的应用．

例2 某个生产计算器公司的管理部门确定每天生产成本函数是：

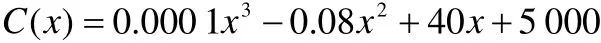
这里x代表生产的计算器数量．（1）求边缘成本函数．（2）求生产200个计算器的边缘成本，并说明其实际意义．

2.2 应用数学课程[5]

除商业微积分外，另一类商业数学课程是应用数学及其在管理和商业科学中的应用，有些大学也称此数学课为有限数学．此课程内容一般包括：函数及图像，指数与对数及应用，金融数学，线性规划及应用，一元微积分及应用．由于篇幅，仅给出两个比较典型的应用例子：一个是金融数学中的应用题目，另一个是线性规划中的应用．

例3 一对夫妇计划为他们已购买的房子再融资．他们现还欠银行150 000元．银行提供两种选择：

1. 利率7.5%（每月复利），30年的期限．

2. 利率7.25%（每月复利），15年的期限．

应该选哪一个，为什么？

例4 一家水果店为欢度节日而准备出售一些水果篮．他们打算卖两种果篮：大篮和小篮．店里一共有200个柑橘，400只苹果．小篮要有6个苹果2个柑橘，其利润是3元．大篮有4只苹果4个柑橘，利润是4元．假设所有的果篮都会售完，那么这家水果店为了得到最大的利润应准备多少大篮，多少小篮？

2.3 以商业课题为主的商业数学[1，6～7]

除了上面提到的两种商业数学课程外，还有些学校开设不同于传统的商业数学．比如在2000年，美国亚利桑那大学数学系和管理学院教授们合作编写了一部比较新颖并富有创新的商业数学教材，又称商业决策中的数学．这本教材不仅仅在内容上有很大的改革，更重要的是其中提出了一个全新的为经济、管理、商业学科学生讲授数学的思路．此教材已由美国数学学会出版，并获得一系列大奖．这个教材包含有两个部分，第一部分以两个商业课题为主导，即以房屋贷款和股票期权定价为主导，通过学习数学工具（概率和模拟），最终对开始提出的课题做出商业决策．第二部分是微积分与优化，这个部分也有两个商业中的课题：石油平台租赁投标和电脑硬盘市场化分析．与第一部分类似，通过数学工具（微积分）的学习，来解决此部分的课题．两部分的特点是通过商业课题为主导，来引出不同的数学内容及工具，用来解决课程中的课题．这里列举一个课题，可以从中领会整个教材的思路．

商业课题 银行信贷课题

某家银行在一年前给一个公司四百万的商业贷款．这个贷款利息是10%，按规定还有4年结束．三周前，这个公司没有按规定支付每月所应偿还的利息．这家银行还发现由于公司现在的整体经营状况，此公司至少下面3个月都没有能力偿还利息．那么摆在这个银行面前的问题是应该止赎还是与此公司再定一个付贷方案．如果选择止赎，银行只能收回两百一十万．如选择重新定付贷方案，就有可能将四百万的贷款及利息全部收回．但如果这个重新付贷方案最终也不成功，银行只能收回两百五十万．决定要不要同这家公司重定付贷方案，这家银行需要知道重新付贷的期望值是多少．

银行现有过去8 000个申请重新付贷成功和失败的记录，在记录中包括老板经营公司的年数，教育背景，及当时经济状况的数据．从现已知信息：这家公司老板经营此公司已7年，他具有商业管理的学士学历，现总体经济状况是萧条，这家银行应该做出什么样的决定，即是止赎还是重定付贷方案，为什么？

3 新问题及挑战

进入21世纪以来，随着科学技术的发展，特别是计算机应用的普及，运用科学技术（泛指计算器，计算机，软件等）在数学教学，商业数学教学中是不可避免的．如何更合理更有效地运用科学技术来提高教学质量是教育工作者面对的一个问题．特别是2008年金融危机带来的教育经费大幅度削减，导致许多像助教这样的教学辅助工作被裁减，过去小班级授课改成大班级授课，远程教育也变成可以节省开支的一个措施．这无疑又加快了科学技术在教学中的应用．另外新时代的大学生们生活在数字时代，对科学技术在学习中的益处比较认同，而且比较容易接受其在教学中的运用．从下面两个实例，可以领略一点使用科学技术在教学的进展．

3.1 大班授课中的Clicker运用[2]

Clicker泛指为课堂互动的学生应对和反应系统．这个系统可以用在即时反馈、投票、测验、考勤等一系列互动教学法中．在课堂中的使用可以促进课堂中的讨论，活跃课堂学习气氛，能够及时地检查学生对授课内容的理解．特别是对于在大班教学中，由于学生人数多，难以进行像在小班课堂里的互动和讨论，Clicker有着明显的可取之处．要有效的使用Clicker在课堂中，还需要与其相配套的课堂问题．使用Clicker方式教学上的题目在数学和物理教学领域通常称为概念测试（ConcepTests），又称Clicker问题．通常是涉及概念的多项选择问题．下面列举几个有代表性的例子．

例5 如给定常数a≠0，下面那个有理函数仅有一个垂直渐近线：

(a)只有(i)；(b)只有(ii)；(c)只有(ii)和(iii)；(d)所有的函数；(e)都没有

例6 下面的表格是一个指数函数的数值：

(b)不正确（False）

例7 某人拿到一份30个月的工作，此工作有两种报酬方式：（1）第一个月公司支付5 000元，以后每月加薪500元．（2）第一个月公司支付1元，第二个月公司支付2元，第三个月公司支付4 元，即每月支付金额是上个月的两倍．

应该选那个方式？为什么？

3.2 网络习题系统

随着计算机网络的普及，网络在数学教学中的应用也越来越广泛，像电子版教材、教学录像、作业、小测验等都可以在网络上实现．特别是网络习题系统逐渐完善，在网络上布置作业，提交作业，并批改作业也都逐渐成了教学中必不可少的辅助工具．许多出版公司竞相推出自己公司出版的教材和特有的网络习题系统．当然绝大多数网络上的习题是多项选择题和填空题．因此，在教学中使用网络习题系统的同时，充分利用传统式的题目来评估学生学习效果仍是个有效的教学方式．

自从2010年苹果公司推出iPad以来，在大学、中学，乃至小学里越来越多的课程已开始使用像iPad一样的平板电脑在课堂教学当中．随着更多的用于平板电脑的教学软件的开发，平板电脑在教学中扮演的角色只会变得越来越大．如何合理并有效地使用iPad等平板电脑在数学教学中是一个全新的课题和挑战．

这里对美国高校商业学科数学教学的现状及发展趋势做一简介，分析和讨论．其它数学课程也面临着类似在商业数学教学中出现的新问题和挑战．

[1] Albers, Donald J. A Genuine Interdisciplinary Partnership: MAA Unveils Mathematics for Business Decisions [J]. Focus, 2002, 22(8): 14-16.

[2] Bode. A Clicker Approach to Teaching Calculus [J]. Notices of the AMS, 2009, 56(2): 253-256.

[3] Barnett, Ziegler, Byleen. Calculus for Business, Economics, Life Sciences, and Social Sciences [R]. 12th Edition, USA, Pearson, 2010.

[4] Tan S T. Applied Calculus: For the Managerial Life and Social Sciences [R]. 9th Edition, USA, Brooks/Cole, 2012.

[5] Tan S T. Applied Mathematics for the Managerial, Life, and Social Sciences [R]. 6th Edition, USA, Brooks/Cole, 2010.

[6] Thompson. Mathematics for Business Decisions Part 1: Probability and Simulation w ith Interdisciplinary Multimedia Projects [R]. Mathematical Association of America, 2005.

[7] Thompson. Mathematics for Business Decisions Part 2: Calculus and Optimization w ith Interdisciplinary Multimedia Projects [R]. Mathematical Association of America, 2005.

On Teaching College Business M athematics in the US, Current and Its Trend

ZHONG Jian-yuan, LU Bin
(Department of Mathematics and Statistics, California State University Sacramento, USA)

Mathematics (often called Business Math) is a required course for business majors at universities in the United States. In this article, we describe different mathematics courses offered for business majors, and compare their contents and emphases of such courses. In addition, we provide several examples of mathematical application problems in business and econom ics. At last, we discuss the areas where technology has been used in teaching business math to enhance teaching and learning effectiveness.

business mathematics; college mathematics; calculus; course content

G40-059.3

：A

：1004–9894（2015）01–0051–03

[责任编校：周学智]

2014–09–01

钟建媛（1972—），女，湖北武汉人，美国加利福尼亚州州立大学萨克拉门托分校数学统计系教授，博士，主要从事低维拓扑、纽结理论和数学教育研究．