基于CI算法的多传感器时滞航迹的分布式融合估计

王光辉，孙书利

(1.天津华能杨柳青热电有限责任公司，天津 300380；2.黑龙江大学 电子工程学院,哈尔滨 150080)

基于CI算法的多传感器时滞航迹的分布式融合估计

王光辉1，孙书利2,*

(1.天津华能杨柳青热电有限责任公司，天津 300380；2.黑龙江大学 电子工程学院,哈尔滨 150080)

网络的传感器节点向处理中心传输局部估计时，不可避免地存在随机延迟，从而导致航迹无序现象频发。在分布式框架下，研究多传感器时滞航迹的融合估计问题。采用最新可利用的局部估计原则，若未收到最新局部估计，则用之前收到的最新的估计进行预报。进而，运用避免计算互协方差阵的CI算法进行分布式融合。避免了计算互协方差阵，且能改善局部估计的精度。仿真例子说明算法的有效性。

无序航迹;CI算法;Kalman滤波方法;多传感器信息融合

0 引 言

随着网络控制系统的快速发展与应用，网络化估计已成为目标跟踪和信号处理等领域的研究热点[1]。数据在网络传输交换中不可避免地受到过程噪声、量测噪声的干扰，同时还受到网络传输协议、网络的传输速率，以及各种传感器不同的预处理时间、通信延迟和传输距离等诸多因素的影响，使得有序采样的信息到达融合中心时呈现无序现象。即后发的信息可能先到，先发的信息可能后到，称为无序信息(“ Out-Of-Sequence ” Information，OOSI)[2-3]。由于无序现象的存在，导致数据不能及时更新，这就为网络环境下的估计、信号处理和控制带来很大挑战，因此研究适用于无序信息系统的估计策略已成为学者们普遍关注的焦点问题[4]。

目前，对于无序信息系统的融合估计研究成果较多的方法是直接更新法，该方法是由Bar-Shalom等在集中式框架下处理无序量测(“Out-of-sequence” Measurements，OOSM)[5]问题时提出的。集中式估计框架即局部传感器向融合中心或汇聚节点传送的是传感器原始量测信息，称为无序量测融合[5-8]。对于单个无序量测的一步延迟的更新估计问题，Bar-Shalom考虑了次优的B1[6]和C1[7]算法中存在而被忽略的相关性问题，提出了在线性最小均方误差(LMMSE)意义下的一步最优无序量测更新A1算法[8]。针对单传感器混合无序量测问题，余安喜等[9]基于LMMSE准则提出了一种可统一处理单、多和混合步延迟的OOSM次优滤波算法。针对多传感器无序量测估计问题，近几年，朱允民团队先后分别提出了多个局部无序量测的最优集中式更新[10]和分布式Kalman滤波融合算法[11]，但由于算法比较复杂，不便于实际应用。葛泉波等在分布式框架下，提出了在分布式框架下解决无序信息的融合估计问题，并取得了一定的研究成果[12-14]。金学波等[15]通过伪测量的分布式融合算法与单步延迟的无序数据最优滤波A1算法组合，给出基于等价量测(伪测量)方法处理航迹无序问题。为了避免互协方差阵的计算，文献[16-17]提出了协方差交叉(CI)融合估计算法。有关应用该算法处理鲁棒融合估计[18]，异步多率融合估计[19]和分量CI融合算法[20]也被报道。

主要考虑在分布式框架下，有序量测信息首先在子节点上进行局部滤波处理，然后当局部滤波估计结果传送到中心处理器过程中存在随机延迟，导致局部滤波估计有序传输无序到达处理中心，则处理中心利用这些无序的局部估计进行相应的融合。笔者利用避免计算互协方差阵的CI融合算法进行融合，得到了比局部估计精度更高的估计结果。

1 问题描述

考虑带L个传感器的线性离散随机系统：

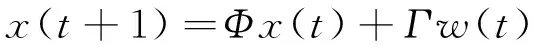
(1)

(2)

其中x(t)∈Rn是系统在t时刻的状态，y(i)(t)∈Rm(i)是状态的观测信号，过程噪声w(t)∈Rr和量测噪声v(i)(t)∈Rm(i)是零均值的白噪声，Φ是n×n维的状态转移矩阵，Η(i)是m×n维的观测矩阵，Γ是n×r维矩阵，上标i表示第i个传感器，L是传感器的个数。

假设1 过程噪声w(t)与量测噪声v(i)(t)相互独立，满足：

(3)

假设2di(t)表示第i个局部传感器向融合中心传输局部估计时的有界随机时滞。

问题是在假设1和假设2下，基于无序局部估计求分布式协方差交叉融合估计。

2 局部最优稳态Kalman预报器

定理1 在假设1和假设2下，具有随机无序航迹的多传感器系统有如下局部最优稳态Kalman预报器：

(4)

(5)

(6)

(7)

(8)

(9)

(10)

(11)

证明 迭代状态方程式(1)di(t)步得：

(12)

则di(t)步预报误差方程：

则di(t)步预报误差方差阵式(11)得证。

将观测方程代入y(i)(t-di(t))得：

(13)

根据假设条件可由标准Kalman滤波器得到：

(14)

同时，可得到式(5)、式(6)、式(8)、式(9)、式(10)。将式(5)和式(6)代入式(14)可得滤波递推形式式(7)。证毕。

3 协方差交叉算法

协方差交叉方法是在信息(协方差)空间内，对均值和协方差估计的一个凸组合的一种融合算法。协方差交叉算法为：

(15)

(16)

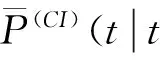
(17)

也可根据黄金分割法来选择ω以达到估计的精度要求。

(18)

4 仿真分析

3传感器跟踪系统：

(19)

(20)

由图1可见，算法具有良好的跟踪效果，在仿真实验过程中做50次Monte-Carlo。由图2可见，CI融合的均方误差位于所有曲线的最下方，说明CI融合估计的精度高于每一局部估计。

(a) 位置预报跟踪图

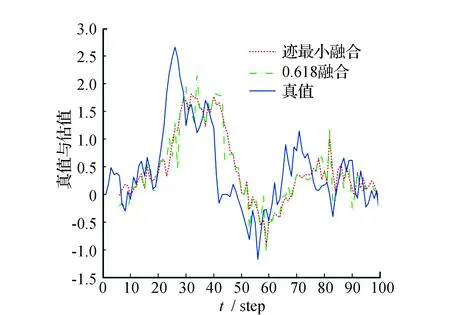
(b) 速度预报跟踪图

(a) 位置的MSE比较图

(b) 速度的MSE比较图图2 CI融合估值器与局部估值器的均方误差(MSE)比较图Fig.2 Comparison of MSEs for local and CI fusion estimators

5 结 论

本文针对在网络数据传输带有随机延迟的情形下，研究无序航迹系统的融合估计问题。由于本文采用的是分布式协方差交叉算法，其不需要计算局部估计误差互协方差阵，与目前常用的3种加权算法相比较，节约了计算时间和计算量，而且也能保证比较精确的滤波结果，同时也避免了集中式框架下处理无序信息融合估计的复杂计算，本文融合方法更具有实用价值。

[1]葛泉波, 冯肖亮, 徐廷梁. 不确定无序量测系统的最优网络化状态估计[J].电子学报, 2011, 39(3A): 7-13.

[2]Ge Q B, Feng X L, Wen C L. Distributed Fusion with Out-Of-Sequence Estimates for Sensor Networks[C]//Cognitive System with Interactive Sensors 2009,Espace Hamelin-Paris, France,2009:16-18.

[3]葛泉波，文成林.多传感器网络系统基于无序估计的分布式信息融合[J].电子与信息学报,2010,7(32):1 614-1 620.

[4]Sun S L, Wen D X. Distributed weighted fusion estimators with random delays and packet dropping [J]. Circuits Systems,Signal Processing, 2007, 26(4): 591-605.

[5]Bar-Shalom, Y. On the Track-to-Track Correlation Problem [J]. IEEE Transactions on Automatic Control, 1981, 26(1): 571-572.

[6]Ge Q B, Wen C L.Decentralized Fusion with Relative Measurements for Delayed Sensor Networks [C]// IEEE International Conference on Macaronis and Automation, Harbin, China, 2007: 366-371.

[7]Bar-Shalom Y, Li X R. Multitarget-Multisensor Tracking: Principles and Techniques [M]. Stors, CT: YBS Publishing, 1995.

[8]Bar-Shalom Y.Update with out-of-sequence measurements in tracking: exact solution [J].IEEE Transactions on Aerospace and Electronic Systems, 2002, 38(3): 769-777.

[9]Yu A X, Liang D N, Hu W D.A Unified Out-of-sequence Measurements Filter[C].IEEE International Radar Conference,Washington ,USA, May 2005: 453-458.

[10]Shen X J, Zhu Y M, Song E B, et al. Optimal centralized update with multiple local out-of-sequence measurements [J].IEEE Transactions on Signal Processing, 2009, 57(4): 1 551-1 562.

[11]Shen X J, Zhu Y M, Song E B, et al. Globally Optimal Distributed Kalman Fusion with Local Out-of-Sequence-Measurements Updates [J].IEEE Transactions on Automatic Control, August 2009, 54(8): 1 928-1 934.

[12]Feng X L, Ge Q B, Wen C L. Optimal Update with One Step Out-Of-Sequence Measurements for Wireless Multi-sensor Network[C]// International Conference on Wavelet Analysis and Pattern Recognition.HongKong, 2008: 826-831.

[13]葛泉波, 王 洵, 管冰蕾. 异步多传感器网络的无序量测融合[C]//2009中国控制与决策会议.2009:4 311-4 316.

[14]葛泉波, 马国进, 汤显峰, 等.噪声相关的一步滞后无序量测递推融合算法[J].传感技术学报.2009, 22(1): 55-66.

[15]金学波, 杜晶晶, 鲍 佳.基于伪测量的分布式最优单步延迟航迹融合估计[J]. 控制理论与应用, 2011, 28(10): 1 451-1 454.

[16]Julier S J, Uhlmann J K. A non-divergent estimation algorithm in the presence of unknown correlation[C] // American Control- Conf, Albuquerque, NM, 1997.

[17]Julier S J, Uhlmann J K. A new extension of the Kalman filter to nonlinear systems[C]// International Symposium on Aerospace/Defense Sensing, Simulation and Controls, 1997: 182-193.

[18]张 鹏，齐文娟，邓自立，等.协方差交叉融合鲁棒Kalman滤波器[J].控制与决策，2012, 27(6): 904-908.

[19]Ma Jing, Lin Honglei, Sun Shuli. Distributed fusion filter for asynchronous multi-rate multi-sensor non-uniform sampling systems[C]// Fusion 2012, Singapore, 1 645-1 652.

[20]林 强，孙书利，基于分量CI融合算法的分布式快速融合滤波器[C]//中国信息融合会议，2014.

CI algorithm based distributed fusion estimation for multi-sensor delayed tracks

WANG Guang-Hui1, SUN Shu-Li2，*

(1.Huaneng Thermoelectric Co.,Ltd at Yangliuqing of Tianjin,Tianjin 300380,China; 2.School of Electronics Engineering, Heilongjiang University, Harbin 150080, China)

When the sensors in networks transmit local estimates to the processing center, there exist random delays inevitably and lead to the phenomenon of out-of-sequence tracks. Based on a distributed framework, the fusion estimation problem for multi-sensor delayed tracks is studied. Using the newest available local estimate principle, if there is no local estimate received in the present moment, the newest local filter received previously will be used for prediction. Further, the CI algorithm which avoids the calculation of cross-covariance matrices is applied for distributed fusion. It not only avoids computing cross-covariance matrices but also improves local estimation accuracy. The simulation example shows the validity of the proposed algorithm.

out-of-Sequence tracks; CI algorithm; Kalman filtering method; multi-sensor information fusion

10.13524/j.2095-008x.2015.03.049

2015-07-13

国家自然科学基金资助项目(61174139)

王光辉(1986-),男，黑龙江齐齐哈尔人，助理工程师，研究方向：时滞系统信息融合估计，E-mail:wgh860625@163.com；*通讯作者：孙书利(1971-),男，黑龙江伊春人，教授，研究方向：状态估计、信号处理、信息融合、传感器网络等，E-mail:sunsl@hlju.edu.cn。

TP274.2

A

2095-008X(2015)03-0068-05