HPM视角下的初中函数概念教学设计

☉江苏省南京市第三十九中学 夏鸣

HPM视角下的初中函数概念教学设计

☉江苏省南京市第三十九中学 夏鸣

一、背景

1972年第二届国际数学教育会议中成立了一个数学史与数学教学关系国际研究小组（简称HPM），它标志着数学史与数学教学关系已作为一个学术研究领域而出现.在数学教学中运用数学史有三种方式：一是提供直接的历史信息；二是借鉴历史进行教学；三是开放对数学及其社会文化背景的深刻觉悟.［1］HPM视角下的数学教学通常采用的是第二种方式，即发生教学法，也就是把数学史作为教学线索，不明确地谈论数学史，用数学史来启示教学.［2］本文在HPM的视角下，以函数概念的教学为例，试图探索符合学生认知发展水平且顺应函数历史发展规律的教学设计，为今后教师在教学中融入数学史提供参考.

二、“函数概念”发展简史

函数一词，最初是在德国数学家莱布尼茨（1646～1716年）1673年的一篇手稿里使用的，但它仅表示关于曲线上点的横坐标与纵坐标，以及一些线段（如弦、切线、法线等）的长.［3］在17世纪，大部分函数都是被当做曲线来研究的，这是函数思想的最初萌芽.

1718年瑞士数学家约翰·伯努利（1667～1748年）把函数定义为“由任一变量和常数的任何形式构成的量”.［4］他强调函数要用公式来表示.

18世纪中期著名数学家欧拉（1707～1783年）在著作《无穷小分析引论》中指出“常量是指永远保持同一值的确定的量”，“变量是指不取定值的量或者说通用的量，它本身蕴含了一切通用的值”，“一个变量的函数是由该变量和一些数或常量以任何一种方式构成的解析表达式”.［5］欧拉用“解析表达式”表述变量之间互相依赖的变化关系，这使人们对函数概念的认识前进了一大步.

1797年法国数学家拉格朗日（1736～1813年）进一步给出了函数的一个定义：“所谓一个或几个量的函数是指任意一个适于计算的表达式，这些量以任意方式出现于表达式中，表达式中可以有（也可以没有）其他一些被称为具有给定和不变值的量，而函数的量值可以取所有可能的量值.因此在函数中，我们仅考虑那些假定是变化的量而不去关心可能包含在其中的常数”.［6］直到18世纪后半期，人们仍然认为函数必须要有解析表达式.

1821年法国数学家柯西（1789～1857年）给出函数的定义：“当给定了变量中的一个值，就可以决定所有其他变量的值的时候，人们通常想象这些量是用其中的一个来表示的，这时这个量就取名为自变量，而由这个自变量表示的其他量就叫做这个自变量的函数”.［4］在柯西的定义中，首先出现了自变量一词，同时指出对函数来说不一定要有解析表达式.

1837年德国数学家狄利克雷（1805-1859年）指出：“如果对于给定区间上的每一个x的值有唯一的y值同它对应，那么y就是x的一个函数，至于在整个区间上y是否按照一种或多种规律依赖于x，或者y依赖于x是否可用数学运算来表示，那都无关紧要”.［7］这个定义与现行初中教科书中的函数定义很接近.它指出函数的本质就是“单值对应”，并且说明函数关系不一定需要用解析式表示.这是人们对函数概念认识上的一次飞跃.

20世纪初诞生的集合论被人们接受之后，函数概念再次发展.1939年布尔巴基学派用集合论的语言重新叙述了函数的定义：“设E和F是两个集合，它们可以不同，也可以相同.E中的一个变量x和F中的变量y之间的一个关系称为一个函数，如果对每一个x∈E，都存在唯一的y∈F，它满足跟x的给定关系，那么我们称这样的‘关系’为函数”.［4］这个定义与现行高中教科书中的函数定义很接近.它是从集合论的角度阐述，用数学自身的逻辑及其特有的抽象，使函数概念更加严密.

纵观函数概念的发展历程，人们先后经历了“几何说”、“代数说”、“对应说”、“集合说”四个阶段，才逐步完善了函数概念，其中从“代数说”到“对应说”是关键，也是最困难的.在初中阶段的函数概念教学中，我们可以适当地借鉴函数概念发展史，改善教学，帮助学生更好地理解函数.

三、“函数概念”教学设计

1.引言

生活中万物皆变，有位置的变化，也有量的变化.如何把握这些量之间的变化规律呢？我们就需要学习新的知识：函数.你们知道历史上数学家对函数概念的研究都经历了哪些阶段？今天我们就沿着数学家的足迹去探究函数的概念.

预设意图：通过引言教学，回顾前面所学知识，提出本节课需要学习的内容，并有机融入函数概念的数学史，激发学生的学习兴趣.

2.函数概念的第一次抽象认识——“代数说”

问题1：列车以200km/h的速度匀速从甲地驶往乙地.当行驶的时间为t h时，行驶的路程为s km.

（1）变量s与变量t之间有怎样的关系？

预设：s＝200t，s随t的增大而增大.

（2）s是怎样随着t的变化而变化的？能用数值加以说明吗？

预设：如表1.

表1

（3）当t取定一个值时，s的值会怎样？你是怎么知道的？

预设意图：以学生熟悉的行程问题为背景，引导学生感受问题中两个变量之间的依赖关系，启发学生发现该问题中的两个变量，当给定一个变量的值时，另一个变量就能用解析式确定唯一的值与其对应，初步体会函数的意义.

问题2：仿照问题1中分析变量关系的过程，分析（1）、（2）中变量之间各有怎样的关系？

（1）某种矿泉水，每瓶价格为1.2元，当销售量为x瓶时，销售金额为y元；

（2）把水滴激起的波纹看成一个不断向外扩展的圆，当它的半径为R时，它的面积为S.

问题3：上述问题中变量之间的关系有何共同特点？

预设意图：解决问题1后，引导学生独立对问题2中（1）、（2）变量之间的对应关系进行分析，同时发现这些实例中的两个变量都能用解析式表示其对应关系，再启发学生对函数概念进行第一次抽象认识.

3.函数概念的第二次抽象认识——“对应说”

瑞士数学家约翰·伯努利认为函数必须要用数学关系式来表示.但是大数学家柯西却提出了质疑：

问题4：下列问题中的变量之间的关系是否具有上述特点？有什么异同？

（1）某厂某种产品的月产量统计如表2.

表2

图1

预设意图：此教学环节为学生提供了两个不能用解析式表示变量之间对应关系的实例，并引导学生体会当给定一个变量的值时，除了借助解析式，通过表格或图像也可以唯一确定另一个变量的值，凸出函数本质属性，剥离“用解析式表示变量关系”这一非本质属性，并对函数概念进行第二次抽象认识.

问题5：德国数学家狄利克雷也认为函数关系不一定需要用数学关系式表示.他还举出了一个例子：y＝人们称之为狄利克雷函数.在实际生活中，存在着大量的函数例子，请你举出一些例子.

预设意图：学生通过自己身边的例子，再次感受函数概念的意义，在不同之中寻找相同，经历从特殊到一般、从具体到抽象、从分散到概括的过程，为最终概括函数概念作进一步准备.

问题6：再次归纳上述所有例子中变量之间的关系具有什么共同特点？

预设意图：在上述活动的基础上，引导学生分步概括、逐步抽象出函数的本质属性，形成函数概念.

4.函数概念的辨析

问题7：下列问题中，两个变量之间是函数关系吗？

（1）用一根2m的铁丝围成一个长方形，当它的宽为x m时，其长为y m；

（2）如图2，搭1条小鱼需要8根火柴棒，每多搭1条小鱼就要增加6根火柴棒.如果搭n条小鱼时，则需要火柴棒S根；

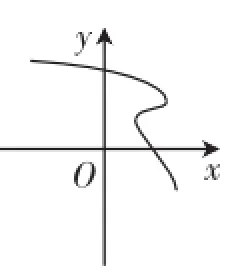
图3

图2

（3）两个变量x、y满足关系式y2=x；

（4）变量y与变量x的关系如图3.

预设意图：通过一些简单的实例，巩固函数概念的学习，规范数学语言的书写与表达.解决问题（3）、（4）时，追问y是x的函数吗？x是y的函数吗？通过正反两方面的例子，深化对函数概念的理解.

问题8：如图4，已知B中的实数与A中的实数之间有着某种对应关系.如果用y表示B中的实数，用x表示A中的实数，那么y是x的函数吗？为什么？

预设意图：一方面帮助学生更深层次地理解函数概念中单值对应的含义，另一方面有意渗透函数概念的“集合说”，为后续函数概念的学习作铺垫.

5.小结

本节课我们模拟了数学史上函数概念发展的过程，分步概括、逐步抽象出函数的概念.

（1）举例说明什么是函数？

（2）你认为函数概念中最关键的语句是什么？并说说对它的理解.

预设意图：回顾函数概念，并引导学生举例说明函数概念的意义.

四、两点感悟

1.以史为鉴，重构课堂

每位学生的认知发展可能各有不同，但总体上都遵循人类认知的一般规律.教学中，我们可以借鉴数学史，启示教学，优化教学.但有时学生对历史上的问题可能会感到陌生与困难，就需要我们重构历史顺序，从学生现有的知识与经验出发，由简单到复杂对问题进行编排.比如，在历史上人们最先认为函数就是一条曲线.但学生在学习函数之前没有接触过图像，他们熟悉的是用字母表示数、公式、方程等.于是教学中，笔者调整了顺序，先引导学生认识函数的“代数说”，再逐步介绍图像确定函数关系的方法.这样的调整不仅遵循学生的认知发展水平，也符合学生学习数学的心理规律.

2.以史为鉴，提升教学

作为数学教师，应该具有一定的数学史知识，了解一些核心知识的起源与发展.在了解历史的过程中，我们会清楚知道数学家们曾遇到哪些困难，犯过怎样的错误.这些都有利于我们了解学生的学习状况，有利于我们在教学中抓住重点、突破难点.比如，函数概念从“代数说”到“对应说”经历了百年之久，数学家们通过一次又一次的修正才得以完善.由此可知，本节课的重点与难点都应该是对函数概念中单值对应含义的理解.教学中，笔者先提供大量正面的实例，通过解析式、表格、图像帮助学生发现变量之间“一对一”、“多对一”的对应关系，再结合一些反例深化学生对函数概念的理解，逐步从“代数说”过渡到“对应说”，并有意渗透“集合说”，最终完善对函数概念的认识.

1.Fauvel J，Van Maanen J.History in Mathematics Education［M］.Dordrecht：Kluwer Academic Publishers，2000.

2.张俊忠.初中数学发生教学法的策略与应用——以北师大版“字母表示数”为例［J］.中学数学（下），2015（3）.

3.林永伟，叶立军，编著.数学史与数学教育［M］.杭州：浙江大学出版社，2004.

4.莫里斯·克莱因.古今数学思想（第3、4册）［M］.上海：上海科学技术出版社，1979.

5.莱昂哈德·欧拉.无穷小分析引论（上下）［M］.太原：山西教育出版社，1997.

6.Dieter Ruthing.函数概念的一些定义——从Jon. Bernoulli到N.Bourbaki［J］.数学译林，1986（1）.

7.A.吉特尔曼.数学史［M］.北京：科学普及出版社，1987.H