基于新版教材下，一道月考试题的命制过程及感悟

基于新版教材下，一道月考试题的命制过程及感悟

☉南京师范大学附属中学新城初中何君青

2011年中华人民共和国教育部制定《义务教育数学课程标准》，针对此次课程标准的实施，苏科版教材内容进行了相应的更改和调整.圆和相似作为“图形与几何”两大重要部分，编排的顺序进行了调整，旧版教材中“圆”为九年级上学期第五章内容，在此之前的初二下学期学生学习了图形的相似等相关知识，而新版教材“圆”调整为九年级上学期第二章内容，图形的相似则调整到九年级下学期学习.面对编排顺序的大幅度调整，给九年级上学期考试的命题工作产生了很大的困难，在此之前，很多有关圆的考题在求线段长的时候经常用到相似的求解方法，这样的调整使得许多经典考题不能再考，在此种背景下，笔者命制了一份学校的九年级上学期月考试卷，其中一道考题打破常规，题目得到了众多老师的称赞，故撰文与同行分享.

一、原题呈现

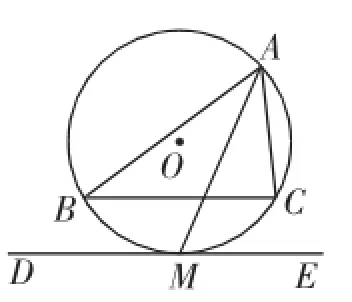
图1

图2

题目如图1，△ABC是⊙O的内接三角形，∠BAC=60°，AB=10，AC=6，AM平分∠BAC，且与⊙O相交于点M，过点M作直线DE，使DE∥BC.

（1）判断直线DE与⊙O的位置关系，并说明理由；

（2）求AM的长.

解析：（1）直线DE与⊙O相切，利用切线的判定定理可以证明.

（2）如图2，连接MB、MC，过点M分别作MH⊥AB，MF⊥AC，垂足分别为点H、F，则∠MHA=∠MHB=∠MFA=90°.

在⊙O中，因为AM平分∠BAC，所以MB=MC.

因为AM平分∠BAC，MH⊥AB，MF⊥AC，所以MH= MF.

所以Rt△AMH≌Rt△AMF，所以AH=AF.

在Rt△HMB和Rt△FMC中，MH=MF，MB=MC，所以Rt△HMB≌Rt△FMC，所以BH=CF.

因为AB=10，AC=6，且AB-BH=AC+CF，所以10-BH= 6+CF，即BH=CF=2，所以AH=AF=8.

因为AM平分∠BAC，∠BAC=60°，所以∠HAM=30°.

评注：本题考查了圆及其有关概念、直线与圆的位置关系、全等三角形的判定和性质、角平分线的性质，同时本题注重思想方法的考查，包含了数形结合、转化的思想，统筹兼顾、相互配合，合理覆盖相关知识、技能和思想方法.此题的考法是常见的中考题考法，中考中第一问常判断直线与圆的位置关系，第二问常求圆中某条线段的长度，以此题为载体，能较好地区分学生学习数学的能力，更好地让学生逐渐适应中考.

二、命题过程

1.初步设想

月考是学校组织的阶段性检测，命题必须以当地中考及《新课标》的要求作为标准，其功能是评价学生一个阶段中对知识的掌握情况，同时这类考试还对教师的后继教学起到指导性作用，所以这类考试无论教师还是学生都要高度重视.

笔者在命题前首先查阅了《新课标》，上面明确规定：理解圆、弧、弦、圆心角、圆周角的概念，了解直线和圆的位置关系，掌握切线的概念，注重学生对所学知识的理解，体会数学知识间的关联.

接着笔者翻阅近几年南京中考试题，发现在近3年中考试题中均出现有关圆的解答题，试题不仅考查了圆的有关性质、直线与圆的位置关系，也考查了学生分析问题、解决问题的能力及综合运用知识的能力，试题的呈现方式经常涉及三角形、平行四边形等几何图形，在求线段的长度时，考题主要运用垂径定理、勾股定理及相似的相关性质.

基于《新课标》的要求，考虑到南京近几年中考试题考查的方式，同时鉴于我校分层教学的情况，笔者决定命制一道难度系数为0.45，考查知识覆盖面广的试题，题目预设为两问，第一问考查直线与圆的位置关系，第二问结合三角形，求圆中某条线段的长度.

2.初稿形成

试题的改编、创作离不开“题源”，而课本却是最好的“题源”地.本着“根在书内，题在书外”这一理念，笔者翻阅新版教材，试图找到突破点，可在“圆”一章中无论是例题还是练习题都未寻找到合适的题目，于是笔者决定把寻找范围扩大，在新版八年级“全等三角形”一章发现有如下这样一道习题：

如图3，在△ABC中，∠BAC＝60°，AM平分∠BAC，MB＝MC，AB＝10，AC＝6，求AM的长.

初看此题，条件很多，感觉应当不难，可是仔细思考后发现并不能快速判断出用何种方法解决此题，于是笔者斟酌再三，决定以此题为背景，加以改编，让题目“穿个马甲”，焕然一新.

笔者曾多次命制期中、期末统考试卷，清楚地认识到在几何题目改编的过程中，常会给几何图形赋予“新的生命”，把几何图形放在平面直角坐标系或圆中，这样会使题目的结论更加丰富，题目更具难度，而且赋予“新生命“后，图形原先所具有的结论仍然存在，笔者命制的试题雏形很快产生了.

在命题初稿时，值得肯定的是本题取材合理：立足基础知识、基本技能，源于课本，高于课本；角度新颖：着眼于几何证明和圆中的相关结论；题型丰富：既有说理又有求值.

3.修订定稿

学生对于圆的相关题目一直有较强的畏惧感，经常看到圆的题目就无从下手，本着尊重学生的原则，笔者将题目的题干、图形尽可能地反复修改，使其尽可能的简洁，以减轻学生的恐惧感.

《新课标》明确提出应当注重发展学生的几何直观、运算能力、推理能力，以往中考试题往往都是比较单一的试题，考查学生对知识的掌握情况，而近3年南京中考试题更多地考查学生的发散思维能力，让不同层次的学生都有展示的空间，凸显出学生应用数学的能力.笔者在修订的过程中，曾试图在第一问铺设台阶，让题目变简单，但为了利用此题拉开学生差距，体现更高的区分度，笔者最终没有铺设台阶降低难度.从试题的发展过程看，第一问考查本学期圆中的相关结论，第二问却结合曾经学习的三角形方面的相关结论进行考查.

4.总结反思

此题的命题角度独特，用全等三角形的背景构建出新题，从八年级的知识考查到九年级的知识，贯穿初中3年，很具典型性，但笔者认为此题还能加以发展，若将该题再发展到平面直角坐标系领域，运用数形结合的思想解决更多的初中数学问题就更完美了，介于时间有限，未曾拓展，确实可惜.

若作为中考前的复习题，此题还可以进一步推广：以BC所在直线作为x轴，BC的垂直平分线作为y轴建立平面直角坐标系，将原图形放在平面直角坐标系内，再将线段的长度换为点的坐标.

图3

三、命题感悟

1.试题评价标准

衡量数学试题质量的高低，要看在符合考试性质的前提下，其试题立意的高低、基本价值立场、价值态度，以及所表现出来的基本价值倾向和对教学的引导与促进作用，即试题的价值取向.一道高质量的试题，反映了命题者对课程改革精神的深度领悟、对数学本质的准确把握和对教学的高期待.对于教师的命题首先应以《新课标》为理念，再查阅多年中考试题，最后找到合适的“题源”，加以模仿，争取创新，这样才能命制出经典好题.区分度和难度是命制试题时特别要控制好的标准，一份试卷必然要有较好的区分度，鉴别优劣，同时难度要控制在一定的范围内，建议月考试卷根据学校学生的情况，难度控制在0.7左右.

2.命题指引教学

在当今教学实践中，仍然存在一定的问题：其一，过程性认识偏浅——事实性现象和事实性知识之间缺少思想方法，缺少逻辑推理的联系、体验，探究活动存在着时间、空间引导与安排上的问题，虽然课堂在探索，但仅局限于浅层次的探索，并未获得该有的深层次的结论，认识较浅；其二，课堂基于“题”的教学——缺少结构性迁移，教师在课堂教学中对题目的开放性不够，常常就题论题，导致题目浅尝辄止，只关注答案的生成，并未关注学生对一类题的解决方法的指导，或者互动、自主设计、学习探究指导不足，故而解题教学过度，学生缺乏基本的经验，并未形成常规的思路，对于题目达不到举一反三，灵活解答.这些教学中的负面价值取向严重遏制了学生数学的发展，所以通过考试试题的命制应当让教师清醒地认识到这点，故在教学时教师应让学生通过自己的思考，理解知识之间的相互联系，建立知识网络，重视对数学知识的理解和数学方法的感悟.H