间隙结构对轮缘密封封严性能及透平级气动性能影响的数值研究

高庆,李军

(西安交通大学叶轮机械研究所,710049,西安)



间隙结构对轮缘密封封严性能及透平级气动性能影响的数值研究

高庆,李军

(西安交通大学叶轮机械研究所,710049,西安)

采用数值求解三维RANS方程和SST湍流模型的方法,研究了间隙结构对轮缘密封封严性能以及封严射流对透平级气动性能的影响。首先,分别对Aachen的一级半透平以及实验测得的轴向轮缘密封结构进行了数值计算,验证了所用数值方法在透平级气动性能以及密封封严性能方面计算的有效性。在此基础上,分析对比了5种封严射流流量下出口面积相同的直缝间隙、倾斜间隙,以及在倾斜间隙基础上改型得到的渐缩、渐扩间隙等4种密封结构的封严性能和封严射流对透平级气动性能的影响。结果表明,轮缘密封间隙结构会影响到间隙射流,进而导致不同间隙结构下透平级总压损失不同。与直缝间隙相比,倾斜间隙可以有效减小封严射流造成的总压损失,同时具有较高的封严性能;渐缩、渐扩间隙的封严性能与倾斜间隙相近,其中渐扩间隙可以更为有效地减小封严射流造成的气动损失。

透平级;涡轮;轮缘密封;气动性能;数值研究

涡轮转、静部件之间有一轮盘腔室,工作时由于主流与盘腔间存在压差,所以高温主流燃气会侵入轮盘腔室而导致涡轮盘过热。为保证涡轮盘安全、可靠地工作,必须对其进行冷却。在盘腔中一般通入由压气机级引入的冷气对涡轮盘及动叶根部进行冷却,同时这部分冷气还将作为轮缘密封封严气流,用来提高盘腔内压力,进而阻止外环高温主流燃气入侵。性能优良的轮缘密封从压气机引入的冷气量较少,却能保证整机效率提高,因此对轮缘密封封严性能和主流透平级气动性能影响的研究具有重要的工程应用价值。

Bohn在1.5级透平实验台上研究了轴向和径向密封对主流入侵上游盘腔的影响[1]。Teramachi等采用实验和数值的方法研究了包含静叶和静叶上游盘腔的4种密封齿结构的轮缘密封封严性能[2]。Narzary在单级透平实验台上对单齿和双重轮缘密封进行了实验研究[3]。Hills等数值研究了主流燃气通过涡轮轮缘密封入侵轮盘腔室的非定常流动特性[4]。Mirzamoghadam对高压透平的轮缘密封燃气入侵特性进行了定常数值研究[5]。Zhou等对轴向轮缘密封的燃气入侵特性进行了数值研究,并采用孔板模型对结果进行了分析[6]。

虽然轮缘密封的设计目的是减少封严冷气量,但是封严冷气汇入主流流道后会影响主流流动形态,进而改变通道内涡系结构,造成气动损失。优良的轮缘密封结构不仅具有好的封严性能,还应使得封严气流导致的气动损失尽可能的小。本文采用求解三维RANS方程和SST湍流模型的方法,从轮缘密封的封严性能及其对透平级气动性能的影响出发,对不同间隙结构的轮缘密封进行了分析,以期为高性能轮缘密封设计提供参考。

1 计算模型与计算方法

1.1 计算模型

以涡轮轴向轮缘密封为对象,开展了直缝间隙、倾斜间隙结构,以及在倾斜间隙结构基础上改型得到的渐缩和渐扩间隙结构的密封封严性能,和通过密封间隙的封严射流对主流透平级气动性能影响的研究。倾斜间隙结构的轴向倾角为45°,改型时出口间隙不变,密封中心线倾角不变。图1给出了密封结构及计算域,密封结构的出口间隙Sc均为8 mm。

(a)直缝间隙

(b)倾斜间隙

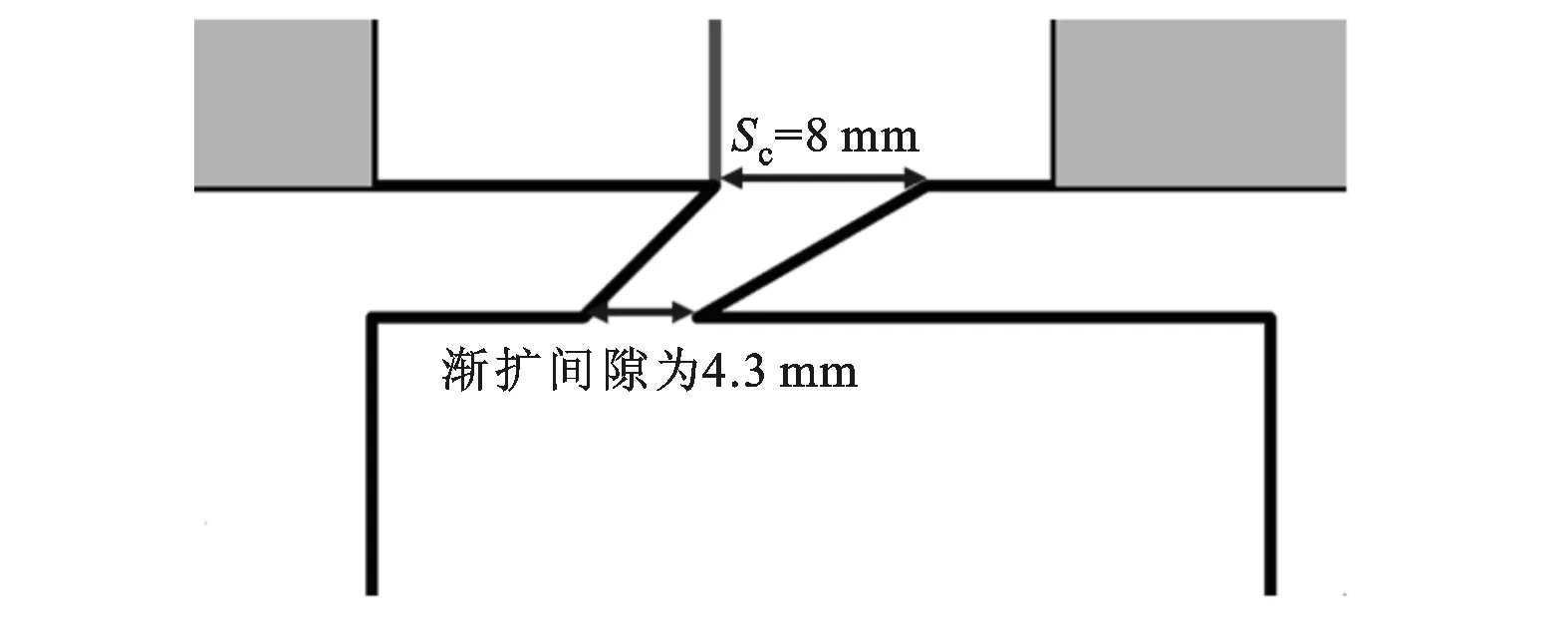
(c)渐扩间隙

(d)渐缩间隙图1 密封结构及计算域

轮缘密封结构的几何参数包括:轮缘密封端面半径b=345 mm,轮缘密封轴向间隙Sc,x=8 mm,轮缘密封径向间隙Sc,r=4.4 mm,盘腔动静间距S=30 mm,轮缘密封轴向间隙比Gc,x=Sc,x/b=0.023,盘腔间隙比G=S/b=0.087。计算时轮缘密封轴向间隙相同,密封出口处间隙位置相同。主流通道中透平级选用文献[7]中的高负荷小展弦比透平叶型,静叶数为30,动叶数为45。

1.2 计算方法及验证

1.2.1 封严效率的计算方法及验证 实验中通常采用CO2浓度法进行轮缘密封的封严效率研究,即在主流中加入示踪气体,通过测量盘腔内固定测点位置的示踪气体浓度来表征主流入侵盘腔的程度及轮缘密封的封严效率。密封浓度封严效率计算如下

εc=(cs-ca)/(c0-ca)

(1)

式中:cs为参考点示踪气体浓度;ca为主流进口示踪气体浓度;c0为冷气流进口示踪气体浓度。

本文通过采用添加附加变量和求解湍流输运方程的方法来模拟示踪气体在主流通道及盘腔内的输运扩散过程。通过求解附加变量湍流输运方程可以获得示踪变量的浓度分布,从而模拟实验中CO2示踪气体分布。湍流流动下的标量输运方程的通用形式如下

(2)

式中:φ为示踪气体的比体积浓度;Sφ为体积源项;Dφ为动能扩散系数(下文简称扩散系数);μt为湍流黏度;Sct为湍流施密特数。

在流动过程中,示踪气体浓度场的形成伴有流动对流传递,同时湍流扩散也会影响浓度场的分布,因此示踪气体扩散系数的确定是准确模拟示踪气体浓度分布的关键。通过与文献[8]实验结果对比发现,本文封严计算方法是可靠的。根据实验工况,计算时扩散系数应在300 K时选取,标准大气压下CO2在空气中的扩散系数为1.6e-5m2/s。

计算中封严射流进口的示踪变量浓度值为1 kg/m3,主流进口浓度值为0 kg/m3。主流入侵和封严冷气流的掺混会导致计算域中示踪变量浓度值介于0和1之间。根据式(1),盘腔处于完全封严状态时浓度封严效率为1,盘腔处于完全入侵状态时浓度封严效率为0。

图2 封严效率计算值与实验值对比

图3给出了主流通道处周向压力系数分布。压力系数定义如下

(3)

图3 主流通道处周向压力系数分布

从图2和图3中可以看出,计算值与实验值吻合良好,从而验证了本文方法在计算轮缘密封封严特性上的可靠性。

1.2.2 透平级气动性能数值方法及验证 为了验证本文透平级气动性能数值方法的可靠性,采用求解RANS方程和SST湍流模型的方法计算了Aachen的1级半透平[9]性能,并与实验数据进行了对比。图4～图6分别给出了1级静叶出口总压、动叶出口总压以及1级静叶出口气流角沿相对叶高的分布。从图4～图6中可以看出,计算值与实验值吻合良好,从而验证了本文方法在预测透平级气动性能上的有效性。

图4 静叶出口气流角沿相对叶高的分布

图5 静叶出口总压沿相对叶高的分布

图6 动叶出口总压沿相对叶高的分布

1.3 网格划分与计算边界条件

图7给出了采用NUMECA-AUTOGRID生成的直缝间隙结构密封的计算网格。主流透平级流道拓扑结构采用H-O-H结构化网格,叶片表面采用O型拓扑贴体网格,叶片进、出口的延伸及盘腔结构为H型结构化网格。生成网格时主流通道与盘腔内在密封间隙处的网格节点要完全匹配,以保证求解的精度。在主流通道中,静叶沿周向布置了55个节点,沿着轴向布置了73个节点;动叶沿周向布置了48个节点,沿着轴向布置了82个节点;主流通道沿叶高方向布置了49个节点;密封间隙布置了30个节点。4种间隙结构的轮缘密封计算网格节点总数为130万～166万,满足网格无关性要求[10],网格最小正交角度为32°。

图7 直缝间隙结构密封的计算网格

计算中工质采用空气,主流进口给定总压Pin=141 860 Pa、总温320 K,主流出口给定平均静压Pout=101 325 Pa,封严射流进口给定质量流量。

定义封严流量比

RM=(m/mm)×100%

(4)

式中:mm为主流质量流量。

本文进行了5种封严射流工况的计算,封严流量比RM分别为0.25%、0.5%、1%、1.5%、2%,m=1.47～11.73 g/s。计算中封严射流进口总温为300 K,旋转域转速为3 600 r/min,固壁面为无滑移绝热壁面,动、静计算域交接面设置在动、静叶中截面且连接方式为级混合面。对流项空间差分采用高精度混合格式,湍流模型为SST模型。当连续方程、动量方程、能量方程、湍流方程的均方根残差达到10-5,各计算域进、出口流量不平衡率小于0.1%时,计算收敛。

2 结果分析

2.1 直缝间隙与倾斜间隙结构的密封性能对比

图8给出了直缝间隙与倾斜间隙结构的轮缘密封封严效率随封严流量比的变化。从图8可以看出:随着封严流量比的增加,2种间隙结构的封严效率均有所提高;当封严流量比小于15%时,倾斜间隙结构的冷却效率均大于直缝间隙结构;当封严流量比大于15%时,2种结构的封严效率区别不大,此时均达到了完全封严状态,封严效率接近100%。

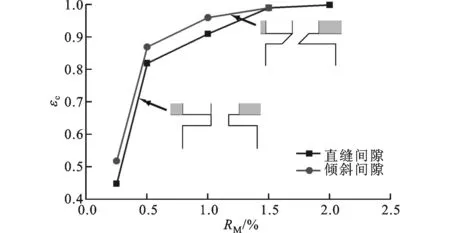
图8 直缝间隙与倾斜间隙结构的轮缘密封封严效率对比

图9 直缝间隙及倾斜间隙结构子午面封严效率分布

图9给出了封严流量比为0.25%时2种间隙结构的子午面封严效率分布。当封严流量比为0.25%时,2种间隙结构均有入侵现象发生。由于转盘旋转带动了封严气流向上运动,所以旋盘一侧的封严效率大于静盘一侧。沿着轴向从静盘面到动盘面,封严效率分布出现了梯度变化,从2种间隙结构可以看出:在动盘面,采用倾斜间隙结构的封严效率相对于直缝间隙结构大大提高,尤其在动盘面靠近密封处表现最为明显。因此,采用倾斜间隙结构可以对承受高温、高压的旋盘提供更为有效的保护。

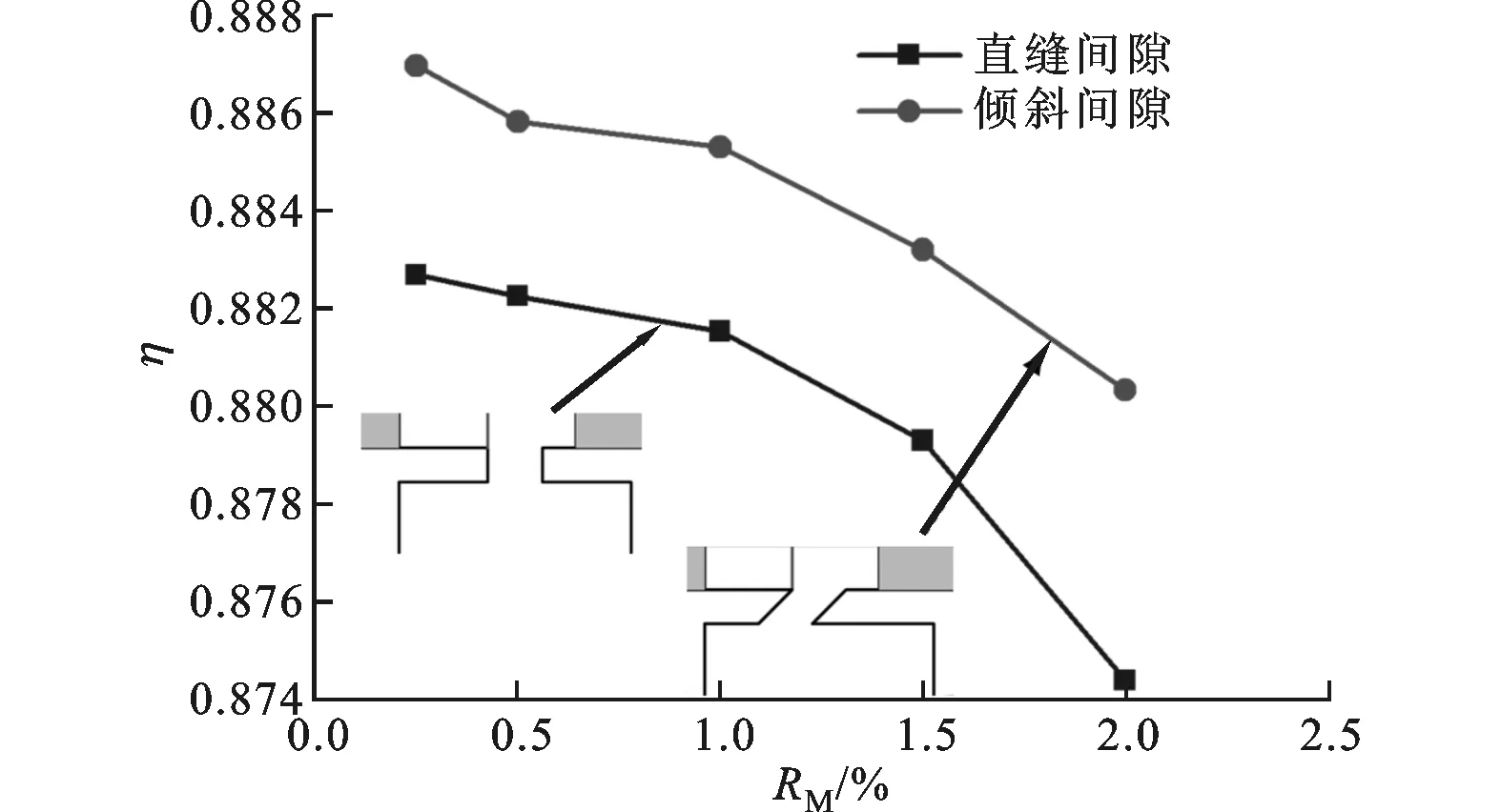
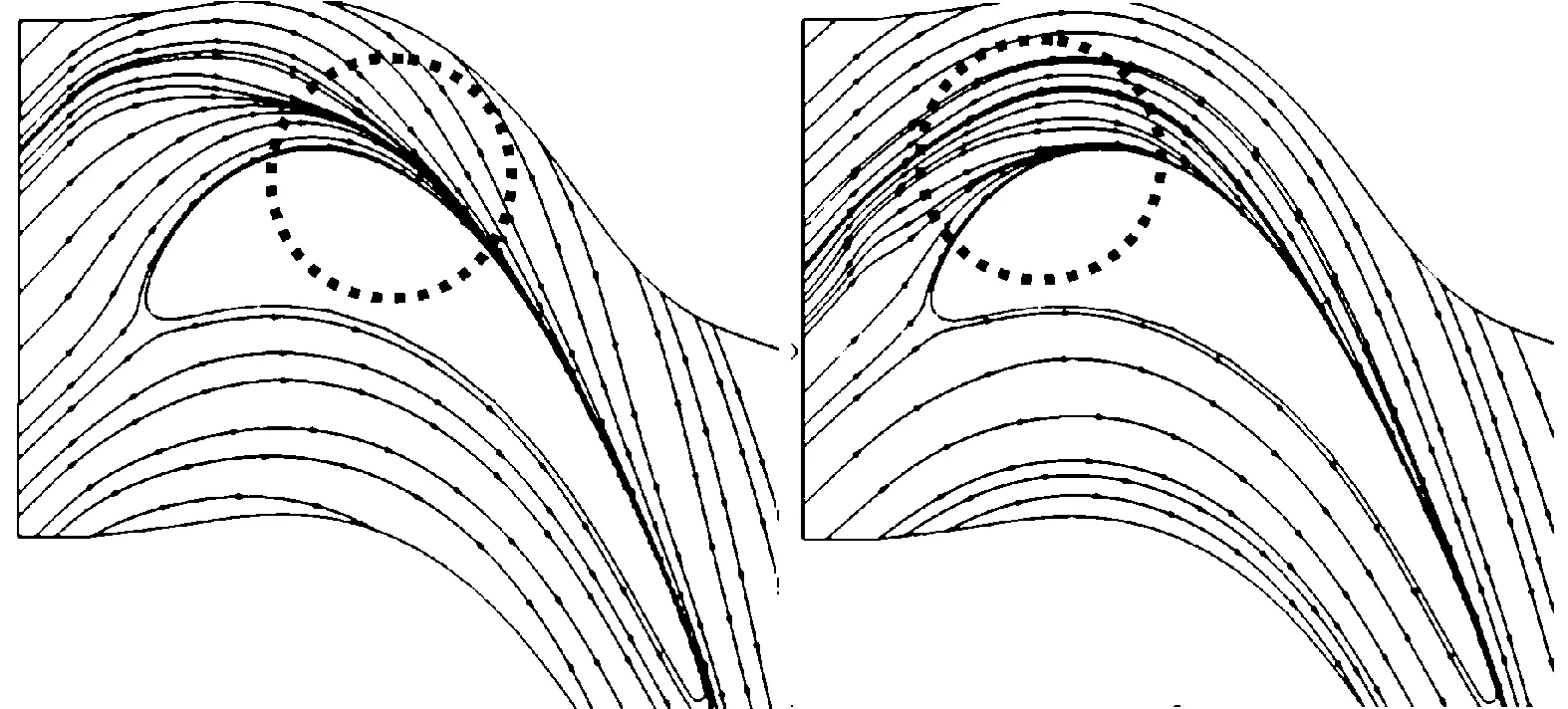
图10给出了直缝间隙及倾斜间隙结构间隙静盘面和动盘面封严效率的径向分布,图中封严效率为周向平均值。从图10可以看出:在静盘面r/b<0.74的低位半径区域,2种密封结构的封严效率区别不大;在r/b>0.74的高位半径区域,倾斜间隙结构的封严效率大于直缝间隙结构;在0.8

(a)静盘面

(b)动盘面 图10 直缝间隙及倾斜间隙结构静盘面和动盘面封严效率的径向分布

本文根据文献[11]中定义,对不同封严流量比下的透平级等熵效率进行了计算。考虑到封严射流潜在的做功能力,定义等熵效率

η=Tqω/(mmCpT0,in(1-(P0,out/P0,in)γ-1/γ)+

mCpT0(1-(P0,out/P0)γ-1/γ))

(5)

式中:Tq为扭矩;ω为转速;T0,in为主流进口总温;T0为封严射流进口总温;P0,out为出口总压;P0,in为主流进口总压;P0为封严射流进口总压。

图11给出了直缝间隙及倾斜间隙结构的透平级等熵效率随封严流量比的变化。从图11可以看出:随着封严流量比的增加,等熵效率降低;当封严流量比从0.25%增加到2%时,直缝间隙结构的等熵效率从0.883降低到0.874,倾斜间隙结构的等熵效率从0.887降低到0.88。对比直缝间隙及倾斜间隙结构发现,5种封严流量工况下倾斜间隙结构的效率均大于直缝间隙结构,表明倾斜间隙结构更有利于提高气动性能,封严射流量愈大,这种优势愈明显。

图11 直缝间隙及倾斜间隙结构的等熵效率对比

图12 直缝间隙及倾斜间隙结构的动叶出口截面总压对比

图12给出了封严流量比为1%时直缝间隙与倾斜间隙结构的动叶出口截面总压对比。受叶栅上、下端壁附近通道涡以及尾迹脱落涡的影响,在动叶出口处形成高损失区。对比2种间隙结构发现,密封结构会对下部通道涡处的高损失区产生影响,而采用倾斜间隙结构的总压损失最小。这是由于:采用直缝间隙结构时,封严射流主要沿径向流出,气流径向速度较大,气流穿透壁面边界层进入了主流通道且对主流产生扰动;采用倾斜间隙结构时,封严射流由于受到倾斜壁面的引导而沿着偏向轴向的方向流出,这样射流会附着在壁面上,使得径向动量减小,对主流穿透的能力减小,进而总压损失减小。

2.2 间隙结构对透平级主流的影响

图13给出了直缝间隙及倾斜间隙结构下动叶在5%叶高处的叶片表面静压分布。从图13可以看出:从吸力面前缘到10%轴向弦长出现了扩压区域,这是封严射流以流动负攻角进入叶片通道,使得前缘附近吸力面压力有所提升所致;2种间隙结构下,压力面静压分布基本一致,吸力面压力分布有所区别,这个现象可以由图14解释,即在周向压力梯度的影响下,随着流动的发展,封严射流进入通道后被推挤到了叶片吸力面。相比于倾斜间隙结构,直缝间隙结构的封严射流会较早地被推挤到叶片吸力面上,导致压力升高,因此在吸力面2种间隙结构下的压力分布有所不同。

图13 直缝间隙及倾斜间隙结构下动叶在5%叶高处的叶片表面静压分布

(a)倾斜间隙 (b)直缝间隙图14 直缝间隙及倾斜间隙结构在0.5%叶高处的流线

出口气流角是反映透平级气动性能的一个重要参数。定义气流角

β=arctan(Wt/WZ)(180/π)

(6)

图15给出了封严流量比为2%时直缝间隙与倾斜间隙结构在动叶出口处的气流角分布。从图15可以看出:在动叶出口区域,不同的间隙结构对中部及下部叶高范围内的气流角会产生影响;在75%以上的相对叶高区域,2种间隙结构的动叶进口气流角分布基本一致;在75%以下的相对叶高区域,采用倾斜间隙结构明显减小了上、下端壁附近二次流引起的气流角欠、过偏转的程度。该结果再次证明了倾斜间隙结构可以减小气动损失。

图15 封严流量比为2%时直缝间隙与倾斜间隙结构在动叶出口处的气流角分布

图16、17分别给出了封严流量比分别为1%和2%时直缝间隙与倾斜间隙结构下主流透平级动叶吸力面极限流线。从图16、17可以看出:极限流线的分离位置基本反映出叶片出口处通道涡的位置;对于直缝间隙结构,封严流量比为1%时动叶出口下部通道涡约位于54%叶高处,封严流量比为2%时动叶出口下部通道涡约位于60%叶高处;对于倾斜间隙结构,封严流量比为1%时动叶出口下部通道涡约位于54%叶高处,封严流量比为2%时动叶出口下部通道涡约位于63%叶高处。封严射流流量发生变化会改变下部通道涡的位置,相比于直缝间隙结构,倾斜间隙结构下部通道涡的位置并没有明显变化。

(a)RM=1% (b)RM=2%图16 直缝间隙结构动叶吸力面极限流线

(a)RM=1% (b)RM=2%图17 倾斜间隙结构动叶吸力面极限流线

2.3 渐缩、渐扩间隙结构的密封性能分析

图18给出了渐缩、渐扩及倾斜间隙结构的封严效率对比。从图18看可以看出:改型后间隙在封严性能并没有明显的变化;当封严流量比达到1.5%时,3种结构均达到了完全封严状态。

图18 渐缩、渐扩及倾斜间隙结构的封严效率对比

图19给出了渐缩、渐扩及倾斜间隙结构的等熵效率对比。从图19可以看出:随着封严射流量比的增加,通道涡强度增强,损失增大,等熵效率降低;相对于倾斜结构,渐扩间隙结构在5种封严射流工况下均有更高的等熵效率,而渐缩间隙结构的等熵效率低于倾斜间隙结构。

图19 渐缩、渐扩及倾斜间隙结构的等熵效率对比

图20给出了封严流量比为1%时渐缩、渐扩及倾斜间隙结构的动叶出口总压分布。相比于倾斜间隙结构,渐扩间隙结构可以进一步减小动叶出口总压损失,而渐缩间隙结构反而增加了动叶出口的总压损失。这是因为,当封严射流经过渐扩通道时,射流速度逐渐降低,射流在汇入主流时的径向速度较小,穿透能力较弱,附着壁面的能力更好,对主流的扰动较小,因而损失较小;反之,当采用渐缩间隙结构时,出口射流径向速度较大,穿透能力较强,气动损失较大。

图20 渐缩、渐扩及倾斜间隙结构的动叶出口总压分布

3 结 论

本文采用三维RANS方程和SST湍流模型研究了4种间隙结构的轮缘密封封严性能和密封间隙射流对透平级气动性能的影响。

相比于直缝间隙结构,采用倾斜间隙结构时的封严效率有所提高,尤其在动盘面且靠近密封处表现得最为明显,同时动叶出口处气流偏转程度减小,通道涡的强度减小,动叶出口总压损失减小。直缝、倾斜间隙结构下的通道涡的位置变化不明显。从封严性能和对主流气动性能影响两方面来看,倾斜间隙结构的密封性能优于直缝间隙结构。

通过对渐扩及减缩间隙结构的研究表明,其在封严性能方面与倾斜间隙结构相近,但在对主流气动性能影响方面,渐扩间隙结构可以更有效地减小动叶出口总压损失。

[1] BOHN D E, DECKER A, MA H W, et al. Influence of sealing air mass flow on the velocity distribution in and inside the rim seal of the upstream cavity of a 1.5-stage turbine, ASME GT2003-38459 [R]. New York, USA: ASME, 2003.

[2] TERAMACHI K, MANABE T, YANAGIDANI N, et al. Effect of geometry and fin overlap on sealing performance of rim seals, AIAA 2002-3938 [R]. Reston, USA: AIAA, 2002.

[3] NARZARY D, FENG F J, ROY R P, et al. Ingestion into a rotor-stator disk cavity with single-and double-rim seals, AIAA 2005-3982 [R]. Reston, USA: AIAA, 2005.

[4] HILLS N J, CHEW J W, TURNER A B. Computational and mathematical model of turbine rim seal ingestion [J]. ASME Journal of Turbomachinery,2002, 124(2): 306-315.

[5] MIRZAMOGHADAM A V, HEITLAND G, MORRIS M C, et al. 3D CFD ingestion evaluation of a high pressure turbine rim seal disk cavity, ASME GT2008-50531 [R]. New York, USA: ASME, 2008

[6] ZHOU D W, ROY R P, WANG C Z, et al. Main gas ingestion in a turbine stage for three rim cavity configurations [J]. ASME Journal of Turbomachinery, 2011, 133(3): 031023.

[7] 孙皓, 宋立明, 李军, 等. 非轴对称端壁透平级气动性能的数值研究 [J]. 西安交通大学学报, 2013, 47(7): 30-35. SUN Hao, SONG Liming, LI Jun, et al. Numerical investigation on aerodynamic performance of turbine stage with nonaxisymmetric end wall profiling [J]. Journal of Xi’an Jiaotong University, 2013, 47(5): 12-17.

[8] SANGAN M C, ZHOU KUNYUAN, OWEN M J, et al. Experimental measurements of ingestion through turbine rim seals, ASME GT2011-45310 [R]. New York, USA: ASME, 2011.

[9] WALRAEVENS R E, GALLUS H E, JUNG A R, et al. Experimental and computational study of the unsteady flow in a 1.5 stage axial turbine with emphasis on the secondary flow in the second stator, ASME 98-GT-254 [R]. New York, USA: ASME, 1998.

[10]高庆, 陶加银, 宋立明, 等. 涡轮轮缘密封封严效率的数值研究 [J]. 西安交通大学学报, 2013, 47(5): 12-17. GAO Qing, TAO Jiayin, SONG Liming, et al. Numerical investigation on the sealing efficiency of the turbine rim seal [J]. Journal of Xi’an Jiaotong University, 2013, 47(5): 12-17.

[11]REID K, DENTON J, PULLAN G C E, et al. The interaction of turbine inter-platform leakage flow with the mainstream flow, ASME GT2005-681551 [R]. New York, USA: ASME, 2005.

(编辑 苗凌)

Numerical Investigations for Effects of Turbine Rim Seal Configurations on Sealing Effectiveness and Aerodynamic Performance of Turbine Stage

GAO Qing,LI Jun

(Institute of Turbomachinery, Xi’an Jiaotong University, Xi’an 710049, China)

The effects of the turbine rim seal configurations on sealing effectiveness and aerodynamic performance of turbine stage are numerically investigated with 3D Reynolds-Averaged Navier-Stokes (RANS) equations and SST turbulent model. The Aachen 1.5 turbine stage and axial rim seal configuration from Bath rig are selected as the research objective. The numerical results coincide well with experimental data. The accuracy of this approach for calculating turbine stage aerodynamic performance and sealing effectiveness are verified. The aerodynamic performance of the turbine stage and sealing effectiveness are comparatively analyzed for five purge mass flow ratios at four kinds of rim seals with different slot geometries. The numerical results show that the slot geometry plays an important role in aerodynamic performance of turbine stage. Compared with straight slot rim seal, inclined slot rim seal reduces total pressure loss in blade passage and also owns the better sealing performance. Two types of new seal, divergent and convergent rim seal, perform as inclined rim seal, and the divergent rim seal configuration facilitates reducing pressure loss.

turbine; rim seal; turbine stage; aerodynamic performance; investigation

2014-06-30。 作者简介:高庆(1988—),男,博士生;李军(通信作者),男,教授,博士生导师。 基金项目:国家自然科学基金资助项目(51376144);中央高校基本科研业务费专项资金资助项目。

时间: 2015-01-05

网络出版地址: http:∥www.cnki.net/kcms/detail/61.1069.T.20150105.0854.005.html

10.7652/xjtuxb201503005

TK474.7

A

0253-987X(2015)03-0025-07