垂直上升内螺纹管中高压汽-水两相流截面含汽率的测量

朱晓静,毕勤成

(1.大连理工大学能源与动力学院,116024,辽宁大连;2.西安交通大学动力工程多相流国家重点实验室,710049,西安)



垂直上升内螺纹管中高压汽-水两相流截面
含汽率的测量

朱晓静1,毕勤成2

(1.大连理工大学能源与动力学院,116024,辽宁大连;2.西安交通大学动力工程多相流国家重点实验室,710049,西安)

利用四头内螺纹管构建了水平绝热管和垂直绝热管组合元件,在压力为11.3、14.2、21.5 MPa,质量流速为250～1 200 kg/(m2·s),热负荷为50～300 kW/m2的范围内,采用压差替代法对内螺纹管内垂直上升流动的高温、高压汽-水两相流进行了截面含汽率的测量,并分析了系统参数对截面含汽率的影响。与经典公式的计算结果对比发现,Zivi模型和我国电站锅炉水动力计算标准与试验数据相差较小,其中Zivi模型与文中试验数据误差小于15%。基于试验数据,分压力拟合了体积含汽率经验公式,与试验值相比绝大部分点的相对误差小于15%,在高干度区相对误差小于10%。研究结果表明,基于压差替代法,采用所提模型可以对垂直内螺纹管内高温、高压汽-水两相流体参数进行有效测量。

内螺纹管;压差替代法;垂直上升;汽-水两相流;截面含汽率

截面含汽率是两相流流动特性中非常重要的参数,它是区分两相流与单相流体不同的重要标识,在研究流动特性和传热特性中必不可少[1]。截面含汽率受流型的影响较大,在不区分流型的情况下,采用现有的截面含汽率计算模型很难取得较高的计算精度。对于高温、高压条件下的管内汽-水两相流体来说,由于高温、高压等条件的限制,一些常用的直接或者间接截面含汽率测量方法,例如快关阀门法[2]、电学法[3]等无法适用,而射线法、吸收法[4]尽管精度相对较高,但受制于测量成本及人身安全等因素而无法在工业生产中广泛推广。

压差替代法是一种基于压差信号的两相流参数测量方法,是指利用相同流动条件下水平段的摩擦压降代替或者计算垂直上升或下降管的摩擦压降,求得垂直管段的重位压降,再利用重位压降与截面含汽率之间的依变关系来求得截面含汽率。对此,已有学者进行了一定的研究工作[5-6]。Barnea实验研究了水平及垂直条件下空气-水两相流的流型,发现在相同的折算汽速和折算液速下,水平流动与垂直向上流动的流型有着非常大的差别,而流型对摩擦阻力及截面含汽率的影响是不容忽视的,因此如果单纯地采用水平管的摩擦压降来代替垂直管的摩擦压降,会给两相流参数的测量带来较大的误差[7]。由此可见,压差替代法进行两相流参数测量的关键是寻求水平管摩擦压降Δpfh与垂直管摩擦压降Δpfv之间的关系。

蔡继勇等人深入研究了空气-油水乳状液在水平管、垂直上升管和垂直下降管内流动时摩擦压降之间的关系,并在此基础上探讨了压差替代法的可行性[8]。其研究结果表明,对于泡状流和环状流可以采用水平管摩擦压降直接替代垂直上升管内的摩擦压降,而对于间歇流动则利用下列形式的公式进行修正

Δpfv=cΔpfh

(1)

式中:下标v和h分别代表垂直上升管和水平管;系数c与工质的物性、管径及系统压力等参数有关。在质量流量很大的极端情况下,流动将趋于均相状态[1],此时c也趋近于1。

前人的研究[9]表明:由于旋流的作用,内螺纹管中汽液两相流体转变为环状流时的折算汽速要远远低于光管内汽液两相流体,即相同条件下,内螺纹管内的两相流体在干度很低的时候就已进入了环状流区域,因此可以认为内螺纹管中流动方向所造成的流型差异对压差替代法的测量精度影响较小。基于这一点,本文利用四头内螺纹管构建了水平绝热管和垂直绝热管组合元件,采用压差替代法对内螺纹管内垂直上升流动的高温、高压汽-水两相流进行了截面含汽率的测量,分析了系统参数对截面含汽率的影响,并将测量结果与现有经典公式的计算结果进行了对比。

1 试验段结构和试验参数

本试验在西安交通大学动力工程多相流国家重点实验室的高温、高压汽-水两相流试验系统上完成,试验回路在文献[10]中已有详细介绍,本文不再重复。图1给出了试验段结构示意图,试验段分为3个部分,即长度为3 500 mm的垂直加热段,长度为2 000 mm的垂直绝热段及水平绝热段。每一段的入口均有长度为600 mm的稳定段,以保证入口流体流型的充分发展。

下标ad表示绝热;he表示加热图1 用于测量截面含汽率的试验段结构示意图

本文的试验参数为:压力p=11.3,14.2,21.5 MPa;热负荷q=50～300 kW·m-2;质量流速G=250～1 200 kg·m-2·s-1。

2 理论模型

圆管内汽液两相流动压降可表示为

Δp=Δpf+Δpa+Δpg

(2)

式中:Δpf为摩擦压降;Δpa为加速压降;Δpg为重位压降。若忽略垂直管及水平管流动方向对摩擦压降的影响,则认为

Δpfv=Δpfh

(3)

因为垂直绝热管和水平绝热管内流动为稳定的绝热流动,故可忽略管内工质的加速压降,即

Δpav=Δpah=0

(4)

对于图1所示的试验段结构,通过压差变送器测得的垂直绝热段和水平绝热段的压降分别为

Δpv=Δpfv+Δpav-|Δpmv-Δpgv|

(5)

Δph=Δpfh+Δpah

(6)

式中:Δpmv为垂直上升管上、下两端取压孔位置差异所造成的压差变送器零点偏置。由于导压管内为常温下的液态水,其重位压降与试验段内工质的重位压降的不同导致了压差变送器的零点偏置,其值为

Δpmv=ρ0gh

(7)

式中:ρ0为环境条件下工质密度;h为垂直上升管的高度。

式(5)中的Δpgv为垂直上升管中工质的重位压降,其值为

Δpgv=ρmgh

(8)

式中:ρm为垂直上升管中工质的截面平均密度,其值为

ρm=φρG+(1-φ)ρL

(9)

其中ρL和ρG分别为液体和汽体的密度,φ为管内工质的截面含汽率。通过式(9)可得

(10)

用式(5)减去式(6),并结合式(3)和式(4),可得

Δpv-Δph=Δpgv-Δpmv

(11)

而垂直绝热管段实际的压降为

Δp=Δpv+Δpmv=Δpv+ρ0gΔh

(12)

将式(8)、式(11)和式(12)联立,可得

Δp=Δpv+ρmgh

(13)

即

ρm=(Δp-Δph)/gh

(14)

将式(14)与式(10)联立,则得到平均截面含汽率计算公式

(15)

式(15)中等号右侧的各变量均可通过试验实测或者水物性程序计算得到,故通过式(15)可获得试验条件下绝热管内汽液两相流平均截面含汽率,即可获得本文所建物理模型中垂直加热段的出口截面含汽率。

3 试验结果及分析

3.1 系统参数的影响

通过将试验数据按照式(15)进行整理,得到了试验条件下垂直加热段出口截面含汽率与垂直加热段出口干度x及体积含汽率β之间的关系。

(a)截面含汽率随干度的变化

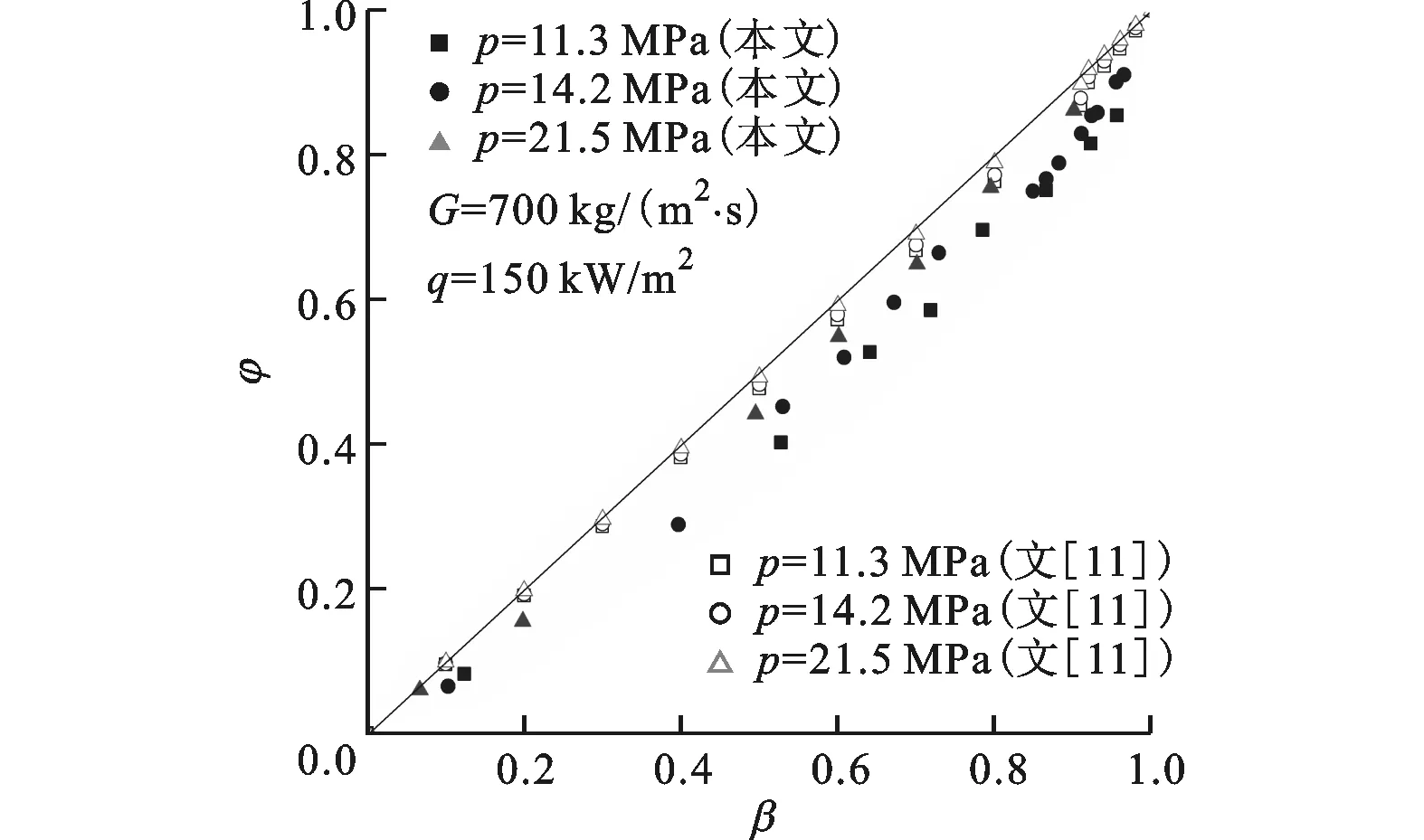
(b)截面含汽率随体积含汽率的变化图2 压力对截面含汽率的影响

图2给出了内螺纹管中系统压力对垂直加热段出口截面含汽率随工质干度及体积含汽率变化的影响,此外图2b还给出本文结果与Armand公式[11]计算结果的比较。Armand公式的获得条件是:压力p≤9 MPa,质量流量W≤0.556 kg/s。从图中可以看出,不同压力下,截面含汽率随工质干度变化的曲线趋势基本相同,即随着干度的增大,截面含汽率逐渐增大,当干度为1时,即管内工质完全汽化时,截面含汽率亦为1。如图2a所示,随着压力的增加,相同干度下汽液两相流截面含汽率减小,并且截面含汽率随干度变化的曲线逐渐趋于平坦。从图2b中可以看出,在试验工况范围内,截面含汽率始终小于体积含汽率,随着压力的增大,截面含汽率和体积含汽率的数值逐渐接近,当系统压力等于临界压力时,φ=β。这是由于当系统压力逐渐增大并接近临界压力时,汽液两相流汽-水密度差减小,抑制了两相分离的能力。通过与Armand公式的比较可以看出,本文试验结果与Armand公式计算结果趋势一致,但数值偏小,其可能的原因在于Armand公式的获得条件,尤其是压力要低于本文的试验工况,并且Armand公式仅考虑了压力对截面含汽率的影响,而本文试验工况则涵盖了压力、质量流速、壁面热负荷及工质热物性等多种因素的影响。图3给出了质量流速对截面含汽率随蒸汽干度变化的影响。在系统压力和管壁热负荷相同的情况下,随质量流速的增加,同一干度时截面含汽率增加。这是因为质量流速增大,则汽相流体与液相流体之间的滑速比减小,截面含汽率因而增大。图4给出了内螺纹管壁面热负荷对截面含汽率随出口干度变化的影响。可以看出,随着内壁热负荷的增加,相同干度下截面含汽率减小。管壁热负荷越大,则工质越容易在管壁面附近形成气泡,因此在相同干度下,汽相速度增大,汽、液间滑速比增大,因此截面含汽率减小。

图3 质量流速对截面含汽率随干度变化的影响

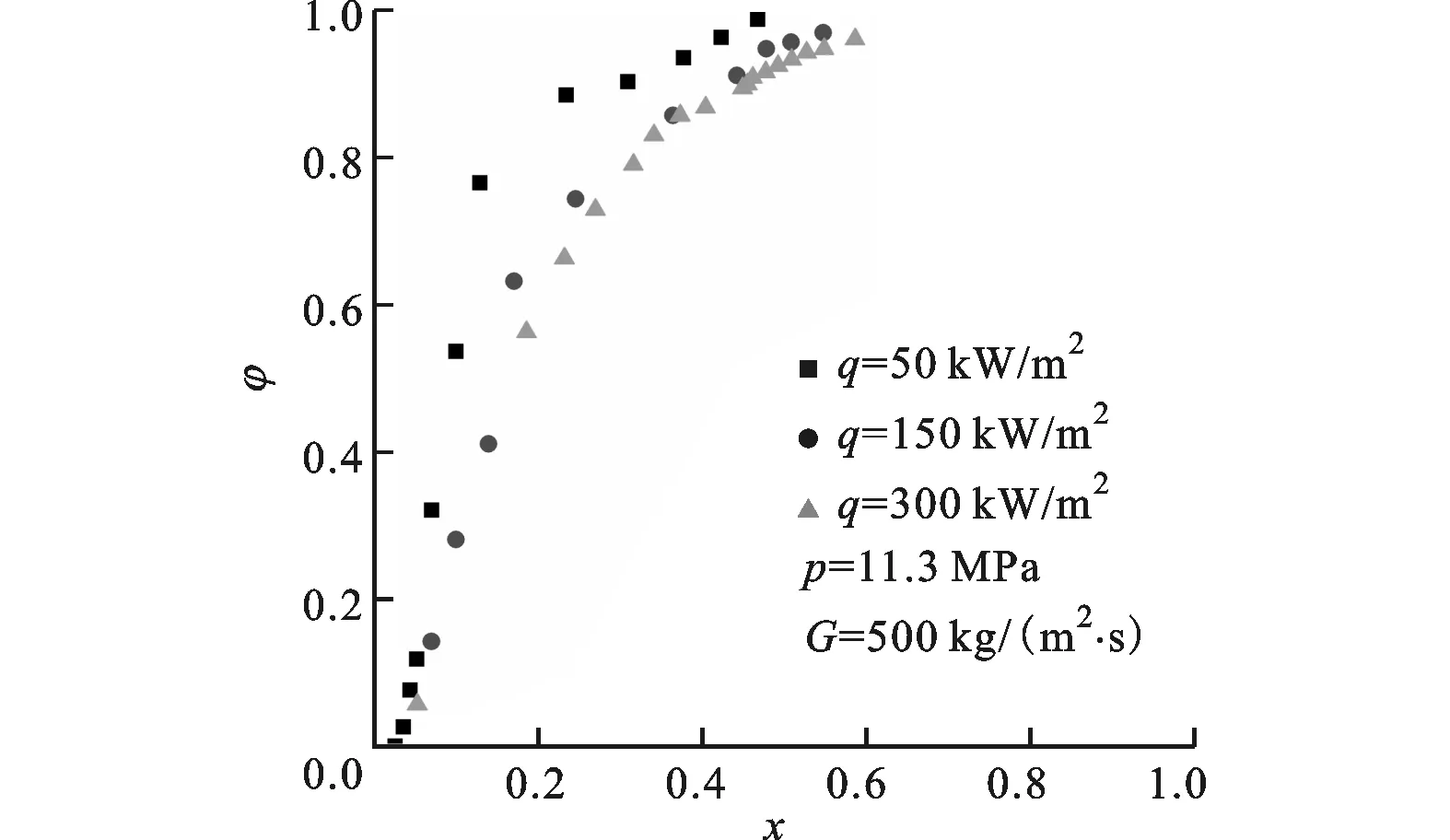
图4 管壁热负荷对截面含汽率随干度变化的影响

3.2 与经典公式的比较

图5a给出了本文模型(式(15))与Armand模型[11]、我国电站锅炉水动力计算方法[12]以及Zivi模型[13]的比较,其中φ为采用式(15)计算所得的截面含汽率,φcal为采用经典公式计算所得的截面含汽率。我国电站锅炉水动力计算方法所给出的公式适用范围是:0.98 MPa≤p≤21 MPa;0.2 m/s≤u0≤4 m/s,u0为全液相流速。Zivi模型是一个基于流动过程中最小熵理论、采用数学方法推导的计算模型,其应用对象为环状流。从图5a中可以看出,在试验工况范围内,本文模型所得出的截面含汽率结果与上述不同模型的计算结果偏差不同。我国电站锅炉计算方法以及Zivi模型所得出的结果与本文模型偏差较小,其中Zivi模型与本文模型相比,90%数据点的相对误差在15%之内。Armand模型与本文模型误差相对较大,部分数据点的相对误差超过30%。图5b给出了某一试验工况下本文模型与上述经典模型所得出的截面含汽率随干度的变化。可以看出,Armand模型由于只考虑了压力对截面含汽率的影响,而忽略了其他参数,故与本文模型的偏差最大,尤其是在高干度区域,误差超过20%。Zivi模型与我国电站锅炉计算方法计算所得出的结果之间相差较小,Zivi模型与本文模型误差小于15%。需要指出的是,在Zivi模型的使用中必须首先确定两相摩擦系数,而内螺纹管内两相摩擦系数受制于内螺纹的结构,不同结构的内螺纹管中两相摩擦系数并不相同,无法采用统一的公式获得较高精度的计算结果,但本文模型则无此限制。

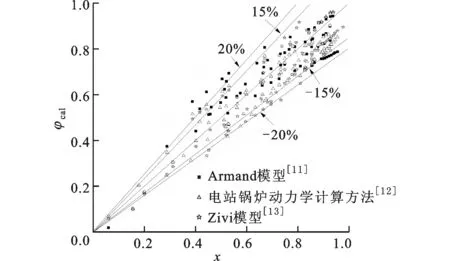
(a)相对误差的比较

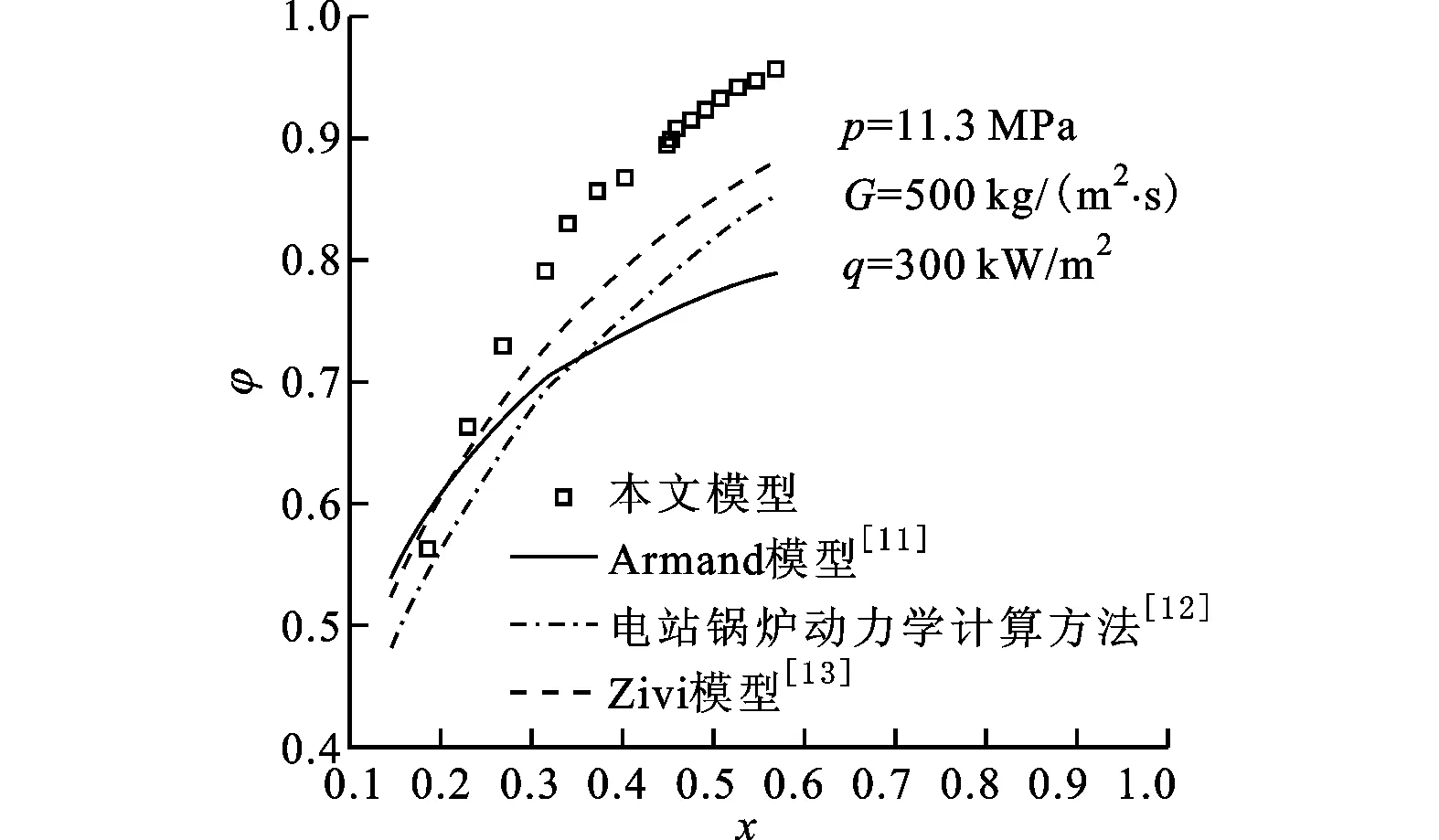
(b)给定工况下截面含汽率随干度变化的比较图5 本文公式与经典公式的比较

3.3 经验公式的拟合

根据Armand的理论,并结合本文所得到的试验结果,可以看出截面含汽率与体积含汽率之间存在较为明确的函数关系,即β=CAφ。对于本文使用的内螺纹管来说,由于管内壁螺纹的旋流作用,密度较大的液体被甩至管壁,而密度较小的汽体则集中在管子中心,故在很大的干度范围内,管内工质的流型为环状流型,这一点与普通的垂直光管有很大的不同。通过对图3和图4的分析可知,质量流速和管壁热负荷对截面含汽率的影响不可忽略,因此在确定系数CA的过程中,必须综合考虑系统压力、工质流量、管壁热负荷及工质物性等诸多因素的影响。CA的一般函数表达式为

(16)

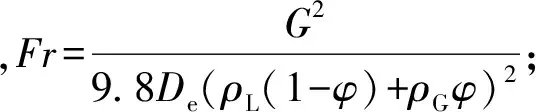
针对本文所研究的内螺纹管中的垂直向上流动来说,We远远大于1.0,即表面张力的作用可以不计,文献[14]的试验结果同样证明了这一点。因此,在式(16)中可以忽略韦伯数对CA的影响,即

(17)

将式(17)无量纲化,得到适用于本文研究对象的CA最终形式为

(18)

(19)

式中:qmax为试验过程中管内壁热负荷的最大值,本文取qmax=300 kW·m-2。在对本文试验数据的整理过程中,采用多元线性回归法,针对每个试验压力,在干度为0～1的范围内,拟合适用于本文试验条件下四头内螺纹管中截面含汽率φ与体积含汽率β之间的关系式。对于高压汽-水两相流来说,高干度区域与低干度区域存在流型差异,因此为了尽量保证所拟合经验关联式的精度,参考Armand模型,以体积含汽率等于0.9为界限,分区域拟合经验关联式如下。

当p=11.3 MPa时

β≤0.9

(20a)

β>0.9

(20b)

当p=14.2 MPa时

β≤0.9

(21a)

β>0.9

(21b)

当p=21.5 MPa时

β≤0.9

(22a)

β>0.9

(22b)

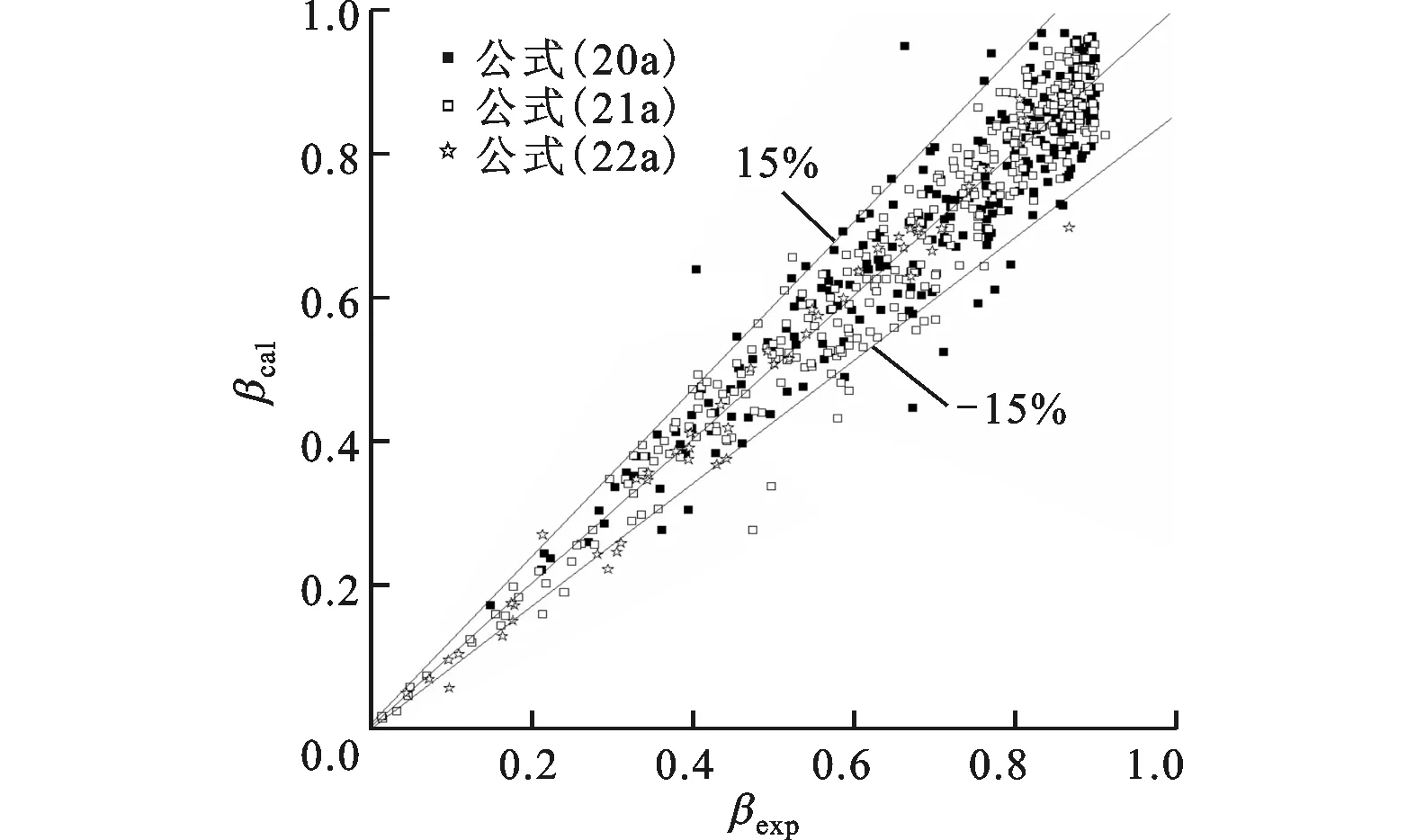
(a)式(20a)～(22a)

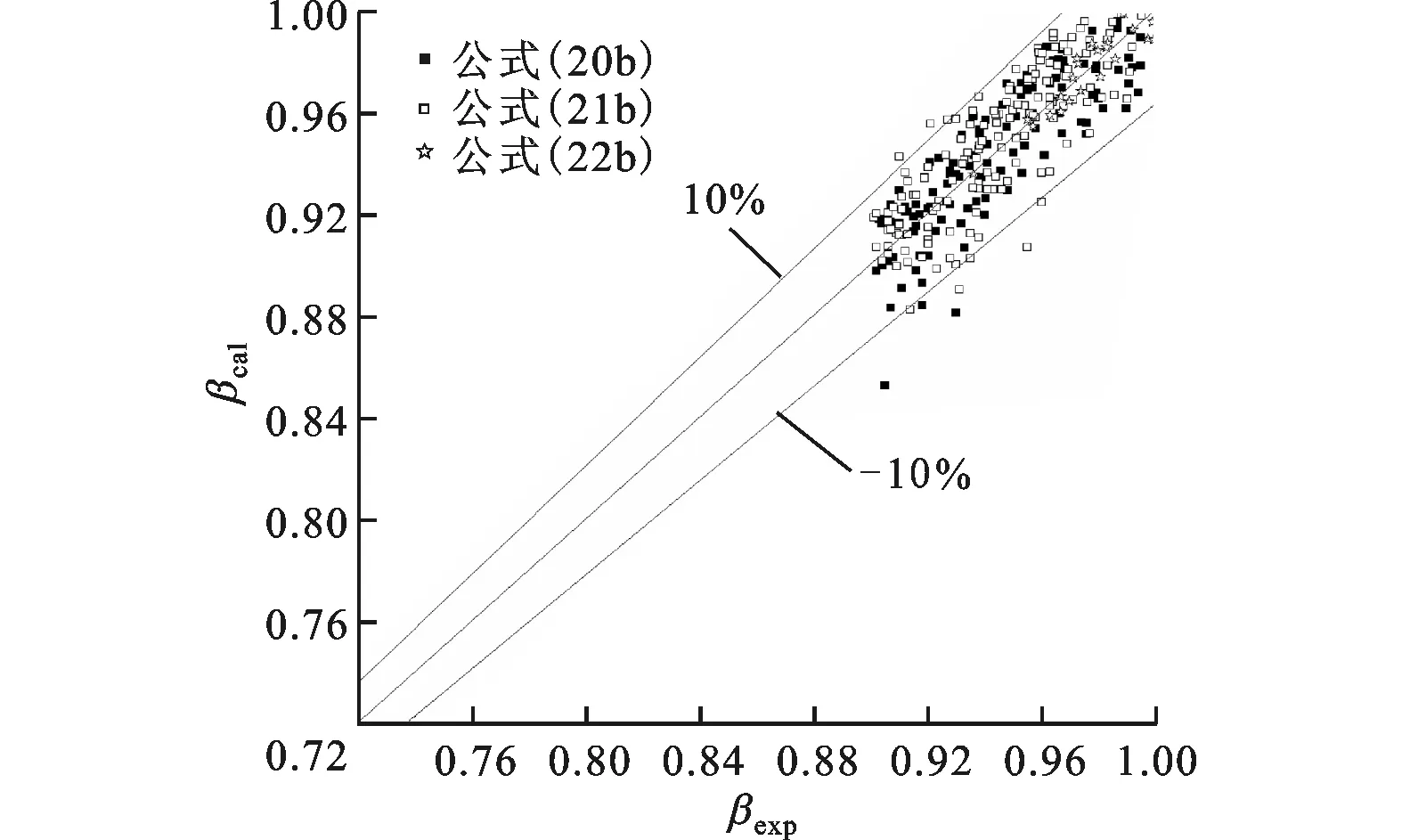
(b)式(20b)～(22b)图6 体积含汽率试验值与计算值的比较

图6给出了采用式(20)～(22)计算所得的体积含汽率预测值与试验所得值的比较结果。从图中可以看出,通过本文所拟合的经验公式得出的体积含汽率计算值与试验值吻合较好,绝大部分点的相对误差小于15%,尤其是在高体积含汽率区域,试验值与计算值之间的相对误差小于10%。

需要指出的是,式(20)～(22)仅适用于本文所涵盖的参数范围,即p=11.3,14.2,21.5 MPa,q=50～300 kW·m-2,G=250～1 200 kg·m-2·s-1。由于压力的改变会导致水和水蒸气热物理性质的较大变化,因此式(20)～(22)外推至其他压力时的精度无法保证,需在后续研究中进一步完善和拓展试验参数范围。

4 结 论

(1)内螺纹的旋流作用导致管内两相流体在较低干度时形成环状流,故可减小相同结构水平管与垂直管内由于流型而造成的两相摩擦压降差异,由此可利用垂直绝热管与水平绝热管的组合元件,采用压差替代法对内螺纹管中垂直上升流动的高温、高压汽-水两相流截面含汽率进行测量。

(2)系统压力、质量流速及热负荷等参数对截面含汽率的影响不可忽略。系统压力增大导致汽液两相流汽-水密度差减小,抑制了两相分离的能力,汽液两相流截面含汽率减小;质量流速增加,汽液滑速比减小,截面含汽率增加;内壁热负荷增加,相同干度下截面含汽率减小。

(3)与现有经典公式的比较结果表明,我国水动力计算方法和Zivi模型与本文模型吻合较好,其中Zivi模型与本文模型的相对误差小于15%,而Armand模型由于仅考虑压力的影响,故与本文模型相差较大。

(4)基于试验数据,在不同压力下拟合了体积含汽率的计算公式,与试验值吻合较好,绝大部分点的相对误差小于15%,在高干度区,相对误差小于10%。

[1] 鲁钟琪. 两相流与沸腾传热 [M]. 北京: 清华大学出版社, 2002.

[2] KOYAMA S, LEE J, YONEMOTO R. An investigation on void fraction of vapor-liquid two-phase flow for smooth and microfin tubes with R134a at adiabatic condition [J]. International Journal of Multiphase Flow, 2004, 30(3): 291-310.

[3] KIM J, AHN Y C, KIM M H. Measurement of void fraction and bubble speed of slug flow with three-ring conductance probes [J]. Flow Measurement and Instrumentation, 2009, 20(3): 103-109.

[4] HRISTOV H V, STEPHAN B, UWE H, et al. A study on the two-phase flow in a stirred tank reactor agitated by a gas-inducing turbine [J]. Chemical Engineering Research and Design, 2008, 86(1): 75-81.

[5] 叶强. 管内汽液两相流流量与相份额的差压式测量方法研究 [D]. 西安: 西安交通大学, 2001.

[6] 朱玉琴. 超临界锅炉汽液两相流分配特性和水动力特性研究 [D]. 西安: 西安交通大学, 2009.

[7] BARNEA D A. Unified model for predicting flow-pattern transitions for the whole range of pipe inclinations [J]. International Journal of Multiphase Flow, 1987, 13(1): 1-12.

[8] 蔡继勇. 圆管内空气-油气乳化液三相流流动特性的研究 [D]. 西安: 西安交通大学, 1997.

[9] ACKERMANN J W. Pseudo-boiling heat transfer to supercritical pressure water in smooth and ribbed tubes [J]. Journal of Heat Transfer, 1970, 3: 490-498.

[10]朱晓静, 毕勤成, 杨冬, 等. 垂直并联管低质量流速自补偿特性的研究 [J]. 核动力工程, 2011, 32(1): 70-74. ZHU Xiaojing, BI Qincheng, YANG Dong, et al. Investigation on self-compensating characteristics of vertical parallel tubes with low mass velocity [J]. Nuclear Power Engineering, 2011, 32(1): 70-74.

[11]ARMAND A A. The resistance during the movement of a two-phase system in horizontal pipes [J]. Izu Vses Teplotekh Inst, 1946(1): 16-23.

[12]上海发电设备所. JB/Z 201—1983 电站锅炉水动力计算方法 [S]. 上海: 上海发电设备所, 1983.

[13]ZIVI S M. Estimation of steady-state steam void fraction by means of the principle of minimum entropy production [J]. Trans ASME: Ser C, 1964, 86: 247-252.

[14]史玉玲. 汽液两相流截面含汽率及流量测量的研究 [D]. 西安: 西安交通大学, 1999.

(编辑 荆树蓉)

Measurement of Void Fraction of High Pressure Steam Water Two-Phase Flow in Vertical Upward Ribbed Tube

ZHU Xiaojing1,BI Qincheng2

(1. School of Energy and Power Engineering, Dalian University of Technology, Dalian, Liaoning 116024, China; 2. State Key Laboratory of Multiphase Flow in Power Engineering, Xi’an Jiaotong University, Xi’an 710049, China)

The void fraction of high-pressure and high-temperature two-phase flow was measured using differential pressure substitute method under the conditions that the pressures are 11.3, 14.2 and 21.5 MPa, the mass velocity ranges from 250 to 1 200 kg/(m2·s), and the heat flux is from 50 to 300 kW/m2. The comparison between experimental data and results of several classical models was conducted. The experimental data agreed with the Zivi model and the model of China’s national standards for hydrodynamic calculation of power station boiler. The relative error between Zivi model and the experimental data is less than 15% and even less than 10% in high quality region. It can be concluded that the method of differential pressure substitute is suitable for the parameter measurement of high-pressure two-phase flow with high temperature in the vertical ribbed tube.

ribbed tube; differential pressure substitute; vertical upward; steam water two-phase flow; void fraction

2014-07-22。 作者简介:朱晓静(1979—),男,讲师,硕士生导师;毕勤成(通信作者),男,教授,博士生导师。 基金项目:国家重点基础研究发展规划资助项目(2009CB219805);中央高校基本科研业务费专项资金资助项目(2342013 DUT13RC(3)069)。

时间: 2014-12-18

网络出版地址: http:∥www.cnki.net/kcms/detail/61.1069.T.20141218.1008.003.html

10.7652/xjtuxb201503009

TK124

A

0253-987X(2015)03-0050-06