21-6-9高强不锈钢管数控弯曲回弹对材料参数的敏感性

方军,鲁世强,王克鲁,唐金星,姚正军

(1.南京航空航天大学材料科学与技术学院,211106,南京;2.南昌航空大学航空制造工程学院,330063,南昌)



21-6-9高强不锈钢管数控弯曲回弹对材料参数的敏感性

方军1,鲁世强2,王克鲁2,唐金星2,姚正军1

(1.南京航空航天大学材料科学与技术学院,211106,南京;2.南昌航空大学航空制造工程学院,330063,南昌)

为了研究材料参数波动对21-6-9高强不锈钢管数控弯曲回弹的影响,结合多因素敏感性分析方法和弯曲-回弹全过程有限元模型,建立了高强不锈钢管弯曲回弹敏感性分析系统模型,并采用该模型研究了高强不锈钢管数控弯曲回弹对材料参数的敏感性。结果表明:回弹半径对材料参数的敏感性大于回弹角对材料参数的敏感性;强度系数是影响高强不锈钢管弯曲回弹最敏感的因素,其次分别为弹性模量、屈服强度、硬化指数和泊松比。通过研究还获得了各材料参数对回弹角和回弹半径的敏感性因子以及当各材料参数的输入值与实际值存在15%的误差时而引起回弹角和回弹半径的相对误差值。研究结果在优化试验方案以及提高弯管回弹预测能力等方面具有重要的作用。

21-6-9高强不锈钢管;材料参数;回弹;敏感性分析;有限元模型

21-6-9(0Cr21Ni6Mn9N)高强不锈钢弯管件由于具有强度高、耐腐蚀和抗氧化等优良特性,并且能够满足对产品轻量化、强韧化和低消耗等方面的需求,在飞机的喷管和液压管路系统等得到了广泛的应用[1]。在压弯、拉弯等众多管材弯曲成形方法中,在多模具约束下数控弯曲可望实现高强不锈钢管精确、高效弯曲成形[2]。然而,由于21-6-9高强不锈钢管具有高的屈弹比,所以弯曲后材料的弹性恢复会导致显著的卸载回弹现象,严重影响着高强不锈钢管数控弯管件的形状和尺寸精度,制约了高强不锈钢弯管件成形质量的提高。另外,由于21-6-9高强不锈钢管材生产工艺的复杂性,以及不同批次生产条件的差异,极易导致材料参数波动,而材料参数影响着复杂加载条件下管材弯曲成形的应力、应变场,进而影响着弯管件卸载后的回弹。因此,研究材料参数波动对21-6-9高强不锈钢管数控弯曲回弹的影响以及回弹对材料参数的敏感性,对于预测和控制回弹、实现数控弯曲精确成形具有重要的理论意义和实用价值。

截至目前,国内外学者针对管材弯曲回弹开展了大量的研究。Al-Qureshi等采用梁弯曲理论,并基于理想弹塑性、平面应变和不考虑包辛格效应等一系列假设,推导出了铝合金薄壁管纯弯下的回弹解析模型[3]。Li等分别采用单因素试验法和基于正交试验的有限元法研究了工艺参数对6061-T4铝合金薄壁管数控弯曲回弹行为的影响规律[4]。E等模拟研究了1Cr18Ni9Ti低强不锈钢管弯曲的时间滞后回弹现象,并且发现随着相对弯曲半径的增加,时间滞后回弹更加显著[5]。Wu等采用试验方法研究了温度、弯曲速度和晶粒尺寸对镁合金管数控绕弯回弹的影响[6]。Li等采用理论解析、显式/隐式三维有限元模拟和物理试验研究了Ti-3Al-2.5V高强钛管数控绕弯的回弹行为[7]。Zhan等针对规格为Φ85 mm×t2.5 mm(管径×壁厚)的CT20钛合金管,采用数值模拟方法研究了CT20钛合金管数控弯曲的回弹机理[8],并提出了一种同时考虑弯曲角和弯曲半径的回弹补偿方法。Zhu等采用多参数敏感性分析法和有限元数值模拟法,研究了H96黄铜薄壁矩形管绕弯回弹和截面畸变对工艺参数的敏感性[9]。关于材料参数对管材弯曲回弹的影响方面,谷瑞杰基于Dynaform有限元平台,研究了材料参数对1Cr18Ni9Ti低强不锈钢管数控弯曲回弹的影响规律[10];李恒等以去应力退火TA18钛管为对象,采用有限元法研究了材料性能波动下钛管绕弯回弹行为,并获得了材料参数波动下高强钛管回弹对截面扁化的影响规律[11];Jiang等基于ABAQUS平台,模拟研究了材料参数和弯曲角度对TA18钛管数控绕弯回弹的耦合影响规律[12]。但是,文献[10-12]的研究中所采用的单因素法均没有考虑材料参数对回弹影响的敏感程度。Zhang等研究了材料参数对TA18高强钛管数控弯曲回弹的敏感性[13],但其采用拟合系统特性和影响因素之间的函数关系来分析材料参数对回弹的敏感性的方法过于繁琐,且需要大量数据来保证拟合精度。以上研究发现,绝大多数是针对铝合金管、低强不锈钢管和钛合金管的弯曲回弹,而在高强不锈钢管弯曲回弹方面以及回弹对材料参数的敏感性方面的研究则鲜有报道。为此,本文以21-6-9高强不锈钢管为对象,结合多参数敏感性分析法和有限元数值模拟法,建立了回弹敏感性分析系统模型,进而揭示了材料参数波动对21-6-9高强不锈钢管数控弯曲回弹的影响规律,以及回弹对材料参数的敏感性。

1 21-6-9高强不锈钢管数控弯曲回弹敏感性分析系统模型

1.1 多因素敏感性分析方法

敏感性分析方法是系统分析中分析系统稳定性的一种方法[14],即分析各影响因素在其各自的可能范围内变动,系统特性偏离基准状态的趋势和程度。在实际系统中,决定系统特性的各因素往往是不同的物理量,具有不同的单位,无法对各因素之间的敏感程度进行比较,因此需要进行无量纲化处理。

定义系统特性P和参数ak的相对误差分别为

(1)

其比值定义为参数ak的敏感度函数,即

k=1,2,…,n

(2)

在|Δak|/ak较小的情况下,Sk(ak)可近似为

(3)

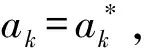
k=1,2,…,n

(4)

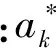
1.2 多因素敏感性分析方法的修正

在进行敏感性分析时首先要建立系统模型,即建立系统特性P和影响因素ak之间的函数关系P=f(ak),k=1,2,…,n,但并不是所有研究对象的系统特性和影响因素之间都具备某种函数关系。另外,对于较为复杂的系统采用数值方法表示系统特性和影响因素之间的关系则需要大量的数据来确保拟合精度。因此,对多因素敏感性分析方法进行修改,修改后的多因素敏感性分析方法为

i=1,2,…,m-1;k=1,2,…,n

(5)

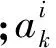
针对本文所研究的21-6-9高强不锈钢管数控弯曲回弹对材料性能参数的敏感性,系统特性P代表回弹角Δθ或回弹半径ΔR,影响因素ak代表材料性能参数,如弹性模量E、强度系数K、屈服应力σ0.2、硬化指数n和泊松比ν。由于高强不锈钢管数控弯曲回弹过程影响因素众多、规律复杂,因此基于ABAQUS软件平台建立有限元模型作为系统模型,研究21-6-9高强不锈钢管数控弯曲回弹对材料性能参数的敏感性。

1.3 数控弯曲-回弹全过程三维有限元模型的建立及可靠性验证

根据实际的管材数控弯曲成形工艺,基于ABAQUS非线性有限元平台、参考文献[16-17]中的建模方法,建立了21-6-9高强不锈钢管数控弯曲回弹全过程三维有限元模型,如图1所示。采用动态显式算法计算弯曲和抽芯过程,采用静态隐式算法计算卸载回弹过程,即采用ABAQUS/Explicit进行弯曲和抽芯模拟,然后把抽芯后的计算结果信息文件作为回弹计算的初始状态导入ABAQUS/Standard进行卸载回弹分析。在回弹分析中包括几何非线性的影响,并采用指定阻尼因子法来计算回弹和应用最大应变能分数来控制回弹稳定性。

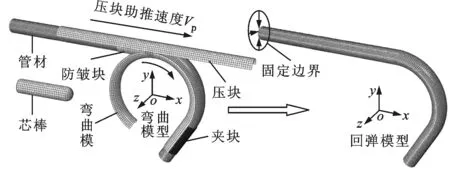
图1 21-6-9高强不锈钢管数控弯曲回弹全过程三维有限元模型

采用4节点四边形壳单元S4R来描述管材,厚度方向选取5个积分点,对弯曲模、夹块、压块、防皱块和芯棒等刚性模具,采用离散刚体单元R3D4来描述其对管材的接触面。采用1.5 mm×1.5 mm、2 mm×2 mm网格分别离散管材和模具表面。根据国标GB/T228.1—2010设计管段拉伸试样,并通过室温单向拉伸试验获得21-6-9高强不锈钢管材的力学性能参数,如表1所示。选取弹塑性本构模型描述管材特性,Ludwigson方程σ=Kεn+Δ表征管材加工硬化特征[18]。采用经典的库仑摩擦模型来描述不锈钢管和模具间的接触行为,不锈钢管与不同模具之间的摩擦系数引用文献[19]中的室温扭转-压缩试验结果,即管材与弯曲模、压块、芯棒、防皱块和夹块的摩擦系数分别为0.1、0.25、0.05、0.05和Rough,其中Rough在软件中表示两接触面一旦接触就不会发生相对滑移,其值取∞。

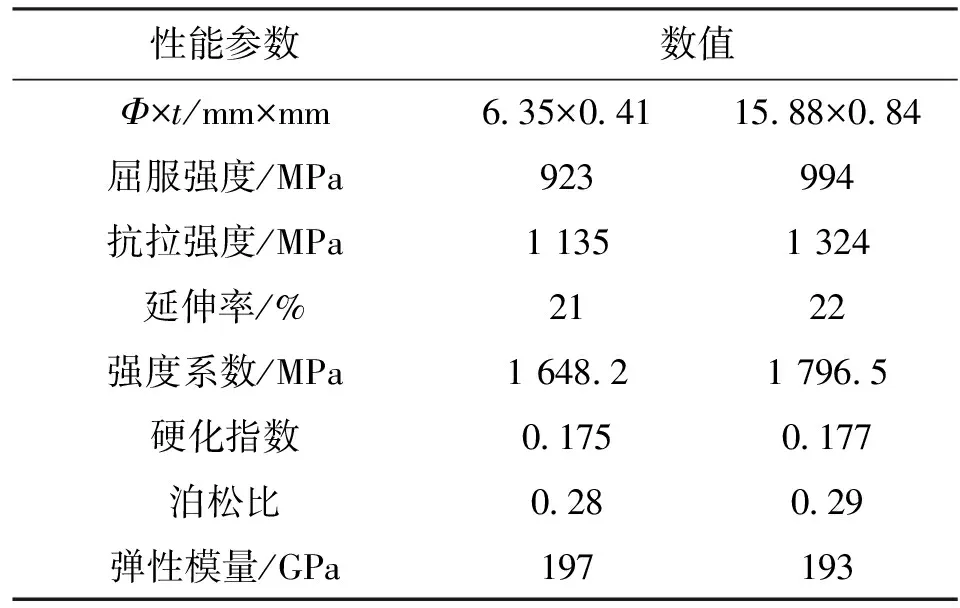
表1 21-6-9管材力学性能参数

采用面-面接触方式定义管材与不同模具间的接触行为,其中管材外表面与模具的接触采用动态接触算法,管材内表面与芯棒的接触采用罚函数法,采用“位移/转动”和“速度/角速度”两种边界条件来反映真实的绕弯过程。弯曲模和夹块采用相同的约束,仅开放绕弯曲模中心转动的自由度,压块只开放沿x轴方向的平动自由度,防皱块的所有位移自由度在弯曲过程中全部被约束,芯棒在弯曲过程中各个自由度为0,在完成设定的弯曲角度后,开放沿x轴方向的平动自由度以实现芯棒的回撤。采用光滑幅值曲线来描述和控制弯曲模、夹块、压块和芯棒的运动,实现平稳的加载过程,以减小惯性效应的影响。卸载回弹过程,所用的模具被移除,并采用固定边界约束来避免刚体运动。

为了验证所建模型的可靠性,针对规格为Φ6.35 mm×t0.41 mm的21-6-9高强不锈钢管,采用SB-12×3A-2S的数控弯管机进行弯曲试验。试验条件:弯曲速度ω为0.4 rad/s,压块助推速度Vp为8 mm/s,弯曲半径R为20 mm,弯曲角度θ为30°、60°、90°、120°、150°、180°,夹块与管材接触面通过砂纸增大摩擦,其他接触面均采用干摩擦。

图2所示为不同弯曲角度下21-6-9高强不锈钢管数控弯曲回弹角的试验结果和模拟结果的对比。由图2可知,模拟和试验得到的回弹角随弯曲角的变化趋势一致,二者的最大相对误差为15.55%,平均相对误差为10.12%,说明本文所建立的三维有限元模型能够真实反映21-6-9高强不锈钢管数控弯曲回弹过程,模拟结果真实可靠,可作为系统模型对弯曲回弹进行敏感性分析。

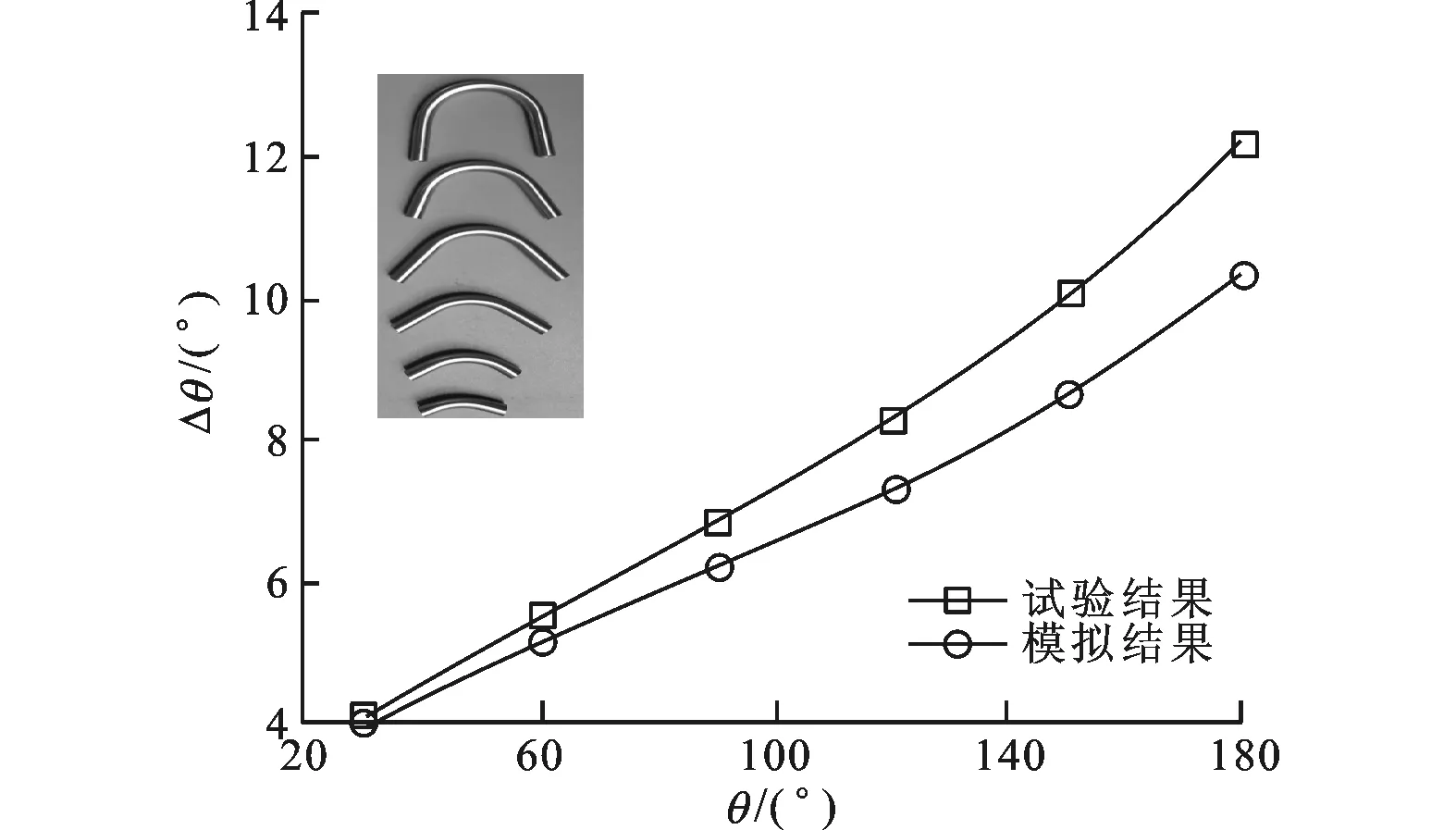
图2 试验结果和模拟结果对比

2 结果与讨论

2.1 研究方案

根据本文和文献[20]中的21-6-9高强不锈钢管材拉伸试验,并适当放大范围以增加研究意义,确定了21-6-9高强不锈钢管材材料参数波动范围,如表2所示,并针对规格为Φ15.88 mm×t0.84 mm的21-6-9高强不锈钢管开展了材料参数波动对数控弯曲回弹的影响以及回弹对材料参数的敏感性研究。

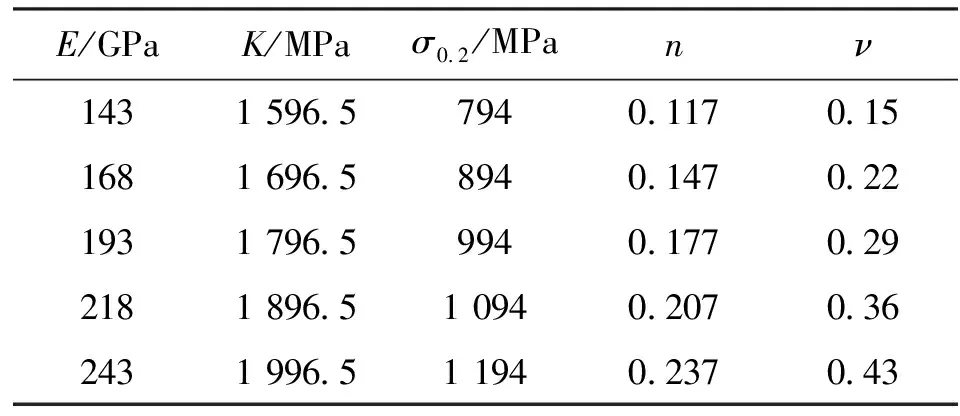
表2 数值模拟中材料参数波动范围

研究中弯曲半径R为47.64 mm,弯曲角度θ为180°,弯曲速度ω为0.4 rad/s,压块助推速度Vp为19.056 mm/s,芯棒伸出量为3.5 mm,管材-夹块间隙为0 mm,管材-芯棒间隙为0.05 mm,其余管材-模具间隙为0.1 mm。

2.2 材料参数波动对回弹的影响

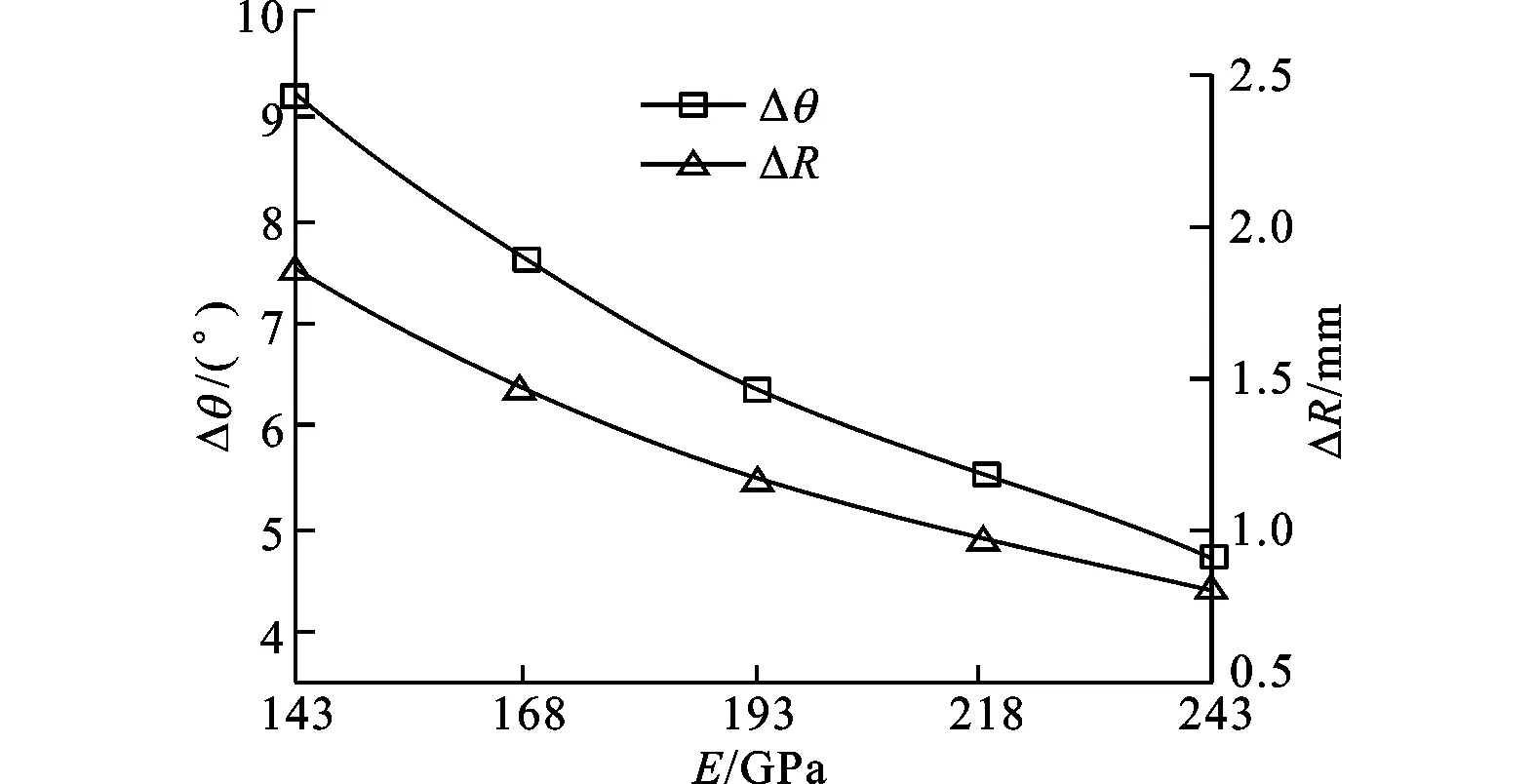
管材弯曲回弹与材料性能有很大关系,因此有必要研究不同材料参数波动对回弹规律的影响,从而为研究回弹对材料参数的敏感性奠定基础。图3所示为材料参数波动对21-6-9高强不锈钢管数控弯曲回弹角和回弹半径的影响。

从图3a中可以看出,随着弹性模量的增加,回弹角和回弹半径逐渐减小。这主要是卸载前的应力与材料的弹性模量共同决定卸载后的弹性回弹量。在只改变弹性模量的情况下,相同规格管材发生相同弯曲变形后的应力大小及分布并无太大差别,而弹性模量越大,同样应变中的弹性应变成分越小,同样屈服应力下的屈服应变越小,表现为回弹角和回弹半径越小。这与弹性模量对低强1Cr18Ni9Ti不锈钢管、中强TA18钛合金管和高强TA18钛合金管弯曲回弹影响规律相似[10-12]。

从图3b中可以看出,随着屈服应力的增加,回弹角和回弹半径逐渐增加。这主要是屈服应力越大,同样应变对应的应力值越大,在弹性模量相同时屈服应变越大,同样应变中的弹性应变就越大,表现为回弹角和回弹半径越大。这与屈服应力对低强1Cr18Ni9Ti不锈钢管、中强TA18钛合金管和高强TA18钛合金管弯曲回弹影响规律相似。

从图3c中可以看出,随着强度系数的增加,回弹角和回弹半径逐渐增大。这主要是强度系数越大,同样应变对应的应力值越大,在弹性模量一致的情况下,同样应变中弹性应变越大,即弯曲角相同时强度系数越大,回弹角和回弹半径就越大。这与低强1Cr18Ni9Ti不锈钢管和中强TA18钛合金管弯曲回弹随强度系数的变化规律相似。

从图3d中可以看出,回弹角随着硬化指数的增加略有减小,但回弹角的变化值不大。根据卸载回弹原理,在相同弯曲条件下硬化指数越大,达到相同变形所需的应力越小,在弹性模量相同时,卸载后弹性回弹量就越小。这与低强1Cr18Ni9Ti不锈钢管、中强TA18钛合金管和高强TA18钛合金管弯曲回弹角随硬化指数的变化规律相似。回弹半径随着硬化指数的增加略有增加,但回弹半径的变化值不大。这与硬化指数对低强1Cr18Ni9Ti不锈钢管数控弯曲回弹半径的影响规律相反[10],而与硬化指数对高强TA18钛合金管数控弯曲回弹半径的影响规律相似[7]。这可能与高强不锈钢管和高强钛合金管具有高的屈弹比有关。

(a)弹性模量的影响规律

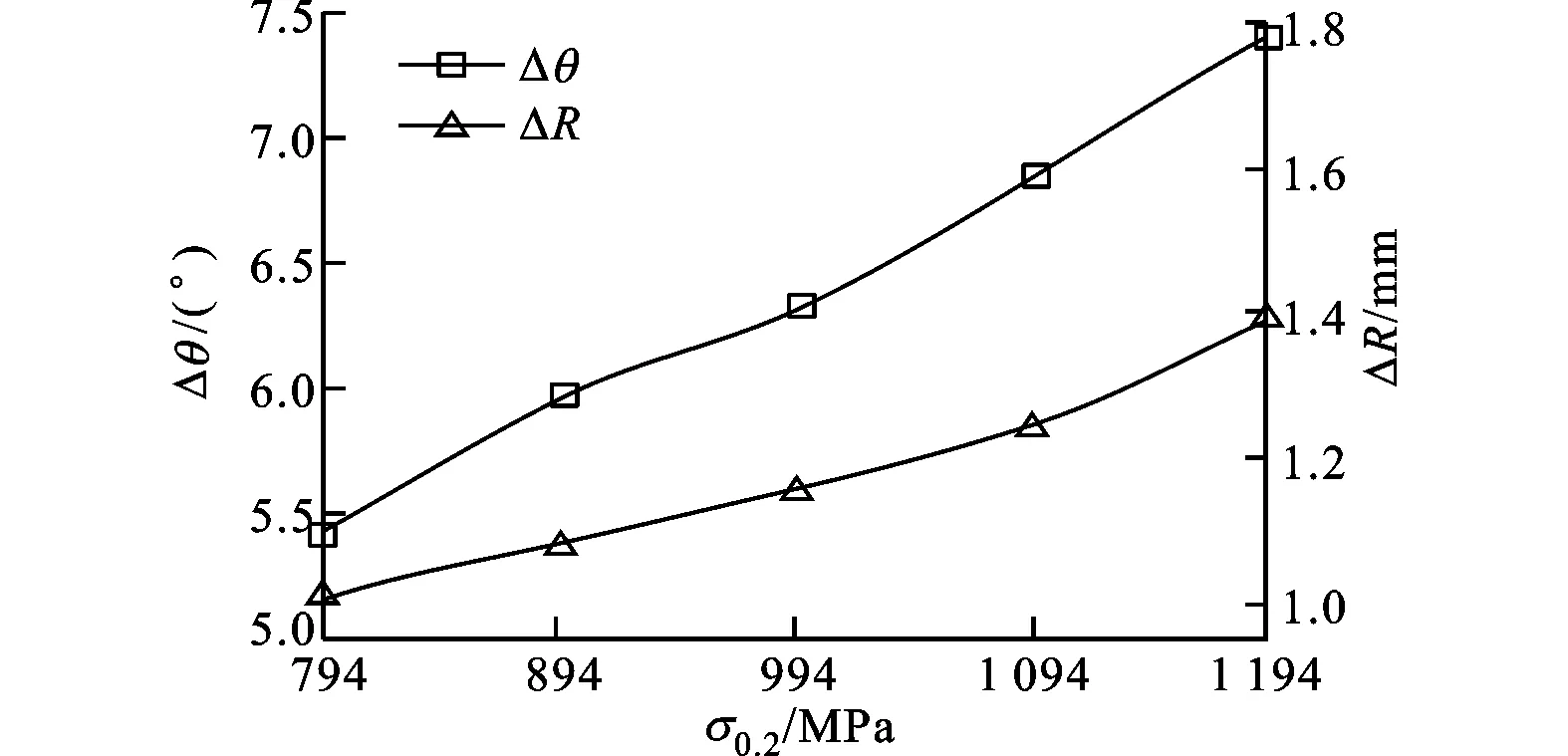
(b)屈服强度的影响规律

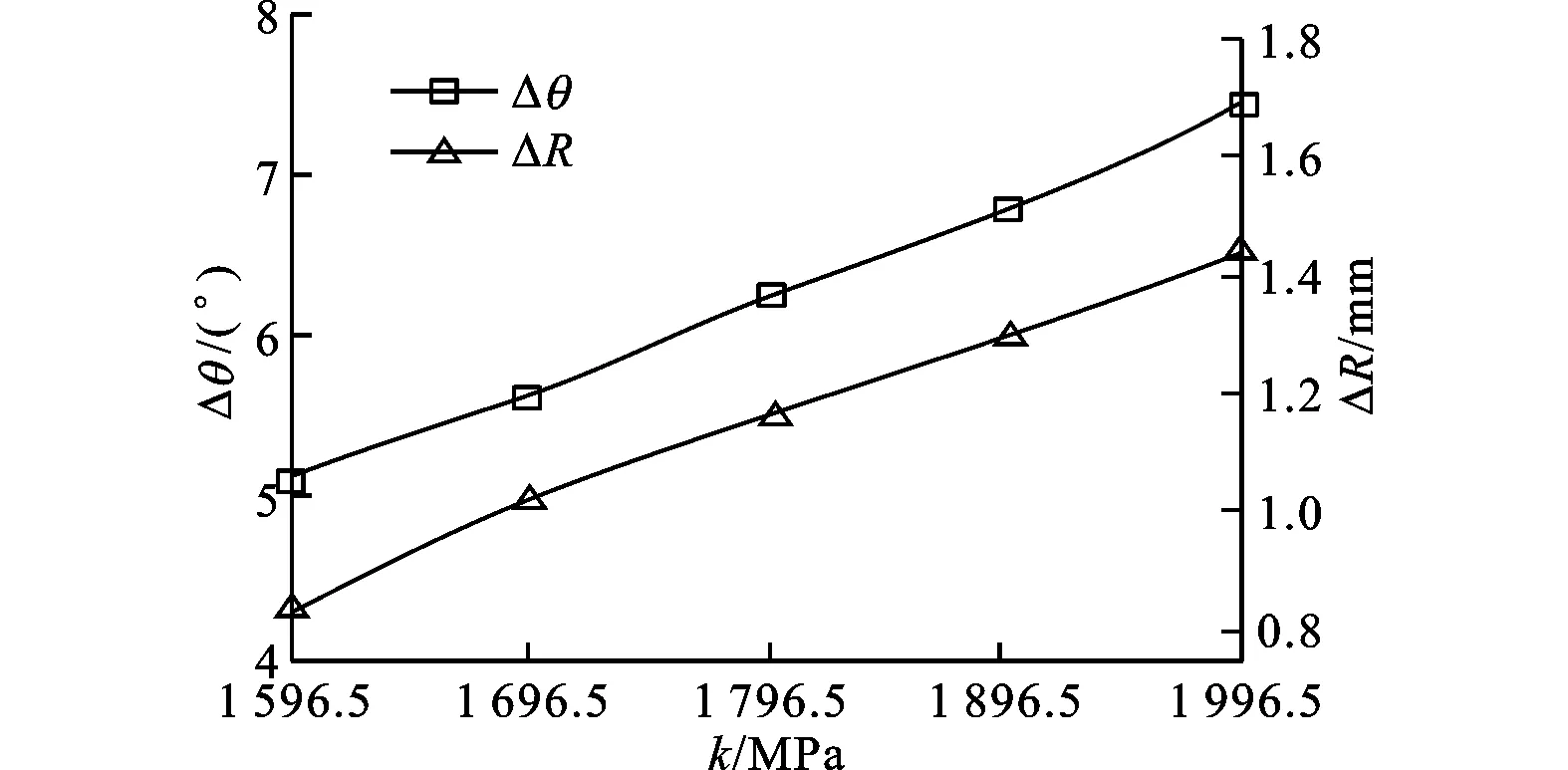
(c)强度系数的影响规律

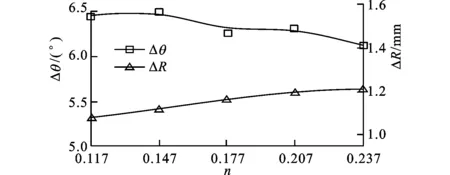
(d)硬化指数的影响规律

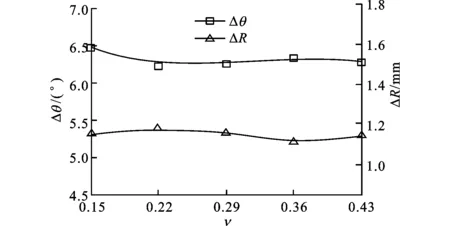
(e)泊松比的影响规律 图3 材料参数波动对21-6-9高强不锈钢管数控弯曲回弹的影响规律

从图3e中可以看出,回弹角和回弹半径随着泊松比的增加略有波动,说明泊松比对回弹角和回弹半径的影响较小。这是由泊松比的物理意义决定的,泊松比是反映材料横向变形的弹性常数,在弹性变形阶段,材料具有不同的且固定不变的泊松比,进入塑性变形阶段后,材料的泊松比都将增大,并趋于极限值0.5,而管材数控弯曲成形属于典型的塑性成形过程,故泊松比对管材数控弯曲回弹的影响较小。

2.3 回弹对材料参数的敏感性

采用表2中的材料参数值,通过式(5)可以求得各材料参数对回弹角和回弹半径的敏感性因子,如表3所示。为了更直观地分析对比21-6-9高强不锈钢管数控弯曲回弹角和回弹半径对材料参数的敏感性,将表3中各材料参数的敏感性因子的值进一步用柱状图表示,如图4所示。

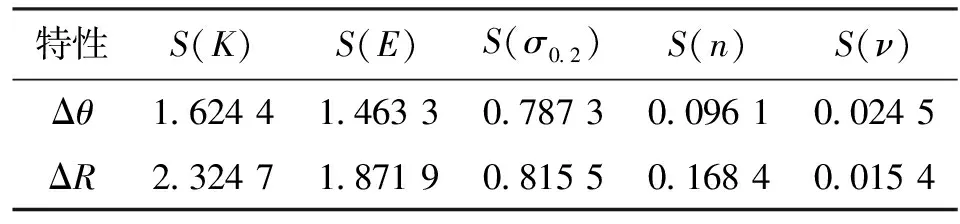
表3 各材料参数的敏感性因子

从表3和图4中可以看出,21-6-9高强不锈钢管数控弯曲回弹半径对材料参数的敏感性总体上大于回弹角对材料参数的敏感性。回弹对K、E和σ0.2较敏感,而对n和ν较不敏感,也就是K、E和σ0.2对回弹影响较大,而n和ν对回弹影响较小,这与2.2节分析的结果相符。由表3和图4还可以看出,21-6-9高强不锈钢管数控弯曲回弹过程中影响回弹角和回弹半径最敏感的因素为K,其次分别为E、σ0.2、n和ν,其中回弹角和回弹半径对K的敏感程度高达1.624 4和2.324 7。换句话说,若K的输入值与实际值相差15%,则由其引起回弹角的相对误差δΔθ=24.36 6%,引起回弹半径的相对误差δΔR=34.870 5%。ν为最不敏感因素,当误差为15%时,由其引起回弹角和回弹半径的相对误差分别仅为0.367 5%和0.231%。同理,可计算出E、σ0.2和n波动15%时,由其引起回弹角和回弹半径的相对误差δΔθ和δΔR,及K和ν波动引起的相对误差值,如表4所示,从而可以判断已知材料参数存在误差时引起的回弹量误差是否在许可的范围之内。

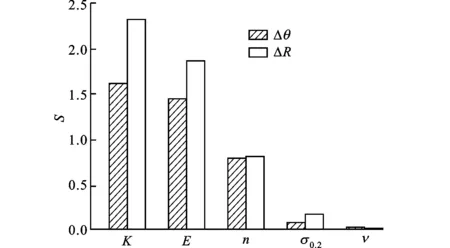
图4 回弹角和回弹半径对材料参数的敏感性对比

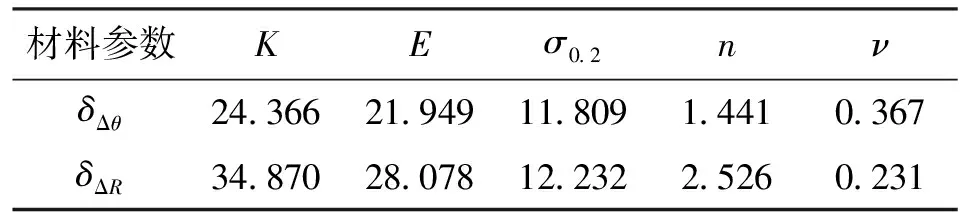
材料参数KEσ02nνδΔθ24366219491180914410367δΔR34870280781223225260231

3 结 论

结合多因素敏感性分析方法和弯曲-回弹全过程有限元模型,建立了21-6-9高强不锈钢管数控弯曲回弹敏感性分析系统模型,并采用该模型研究了高强不锈钢管数控弯曲回弹对材料参数的敏感性,获得的主要结果和结论如下。

(1)采用弯曲-回弹全过程有限元模型,研究了材料参数波动对弯曲回弹的影响,发现回弹角和回弹半径随着K、σ0.2的增加或随着E的减小而增加,n和ν对回弹的影响较小。

(2)借助多因素敏感性分析方法,获得了21-6-9高强不锈钢管数控弯曲回弹对材料参数的敏感性大小及敏感度因子。K为最敏感的因素,其次分别为E、σ0.2、n和ν,它们对回弹角和回弹半径的敏感度因子分别为1.624 4和2.324 7、1.463 3和1.871 9、0.787 3和0.815 5、0.096 1和0.168 4以及0.024 5和0.015 4。当各材料参数的输入值与实际值相差15%时引起回弹角和回弹半径的相对误差分别为24.366%和34.870 5%、21.949 5%和28.078 5%、11.809 5%和12.232 5%、1.441 5%和2.526%以及0.367 5%和0.231%。

(3)回弹半径对材料参数的敏感性大于回弹角对材料参数的敏感性。回弹对K、E和σ0.2较敏感,而对n和ν不敏感。

[1] 王义衡, 马竹叶, 曹建林. 0Cr21Ni6Mn9N耐高温不锈钢及其在冲压发动机上的应用 [J]. 推进技术, 1985, 6(4): 80-87. WANG Yiheng, MA Zhuye, CAO Jianlin. 0Cr21Ni 6Mn9N high temperature resistance stainless steel and its application in ramjet [J]. Journal of Propulsion Technology, 1985, 6(4): 80-87.

[2] YANG He, LI Heng, ZHANG Zhiyong, et al. Advances and trends on tube bending for ming technologies [J]. Chinese Journal of Aeronautics, 2012, 25(1): 1-12.

[3] AL-QURESHI H A, RUSSO A. Spring-back and residual stresses in bending of thin-walled aluminum tubes [J]. Materials and Design, 2002, 23(2): 217-222.

[4] LI Heng, SHI Kaipeng, YANG He, et al. Springback law of thin-walled 6061-T4 Al-alloy tube upon bending [J]. Transactions of Nonferrous Metals Society of China, 2012, 22(sl2): 357-363.

[5] E Daxin, LIU Yafei. Springback and time-dependent springback of 1Cr18Ni9Ti stainless steel tubes under bending [J]. Materials and Design, 2010, 31(3): 1256-1261.

[6] WU Wenyun, ZHANG Ping, ZENG Xiaoqin, et al. Bendability of the wrought magnesium alloy AM30 tubes using a rotary draw bender [J]. Materials Science and Engineering: A, 2008, 486(1/2): 596-601.

[7] LI H, YANG H, SONG F F, et al. Springback characterization and behaviors of high-strength Ti-3Al-2.5V tube in cold rotary draw bending [J]. Journal of Materials Processing Technology, 2012, 212(9): 1973-1987.

[8] ZHAN Mei, ZHAI Huadong, YANG He. Springback mechanism and compensation of cryogenic Ti alloy tube after numerically controlled bending [J]. Transactions of Nonferrous Metals Society of China, 2012, 22(sl2): 287-293.

[9] ZHU Yingxia, LIU Yuli, YANG He. Sensitivity of springback and section deformation to process parameters in rotary draw bending of thin-walled rectangular H96 brass tube [J]. Transactions of Nonferrous Metals Society of China, 2012, 22(9): 2233-2240.

[10]谷瑞杰. 薄壁管数控弯曲回弹研究 [D]. 西安: 西北工业大学, 2008.

[11]李恒, 杨合, 宋飞飞, 等. 材料性能波动下TA18钛管绕弯回弹行为 [J]. 稀有金属材料与工程, 2014, 43(1): 64-71. LI Heng, YANG He, SONG Feifei, et al. Springback rules of TA18 titanium tube upon rotary draw bending under variations of material properties [J]. Rare Metal Materials and Engineering, 2014, 43(1): 64-71.

[12]JIANG Z Q, YANG H, ZHAN M, et al. Coupling effects of material properties and the bending angle on the springback angle of a titanium alloy tube during numerically controlled bending [J]. Materials and Design, 2010, 31(4): 2001-2010.

[13]ZHANG P P, ZHAN M, HUANG T, et al. Sensitivity analysis of material parameters on spring-back of NC bending of high-strength TA18 tube [J]. Advanced Materials Research, 2012, 472/473/474/475: 1003-1008.

[14]陈立周. 稳健设计 [M]. 北京: 机械工业出版社, 2000: 11-15.

[15]章光, 朱维申. 参数敏感性分析与试验方案优化 [J]. 岩土力学, 1993, 14(1): 24-28. ZHANG Guang, ZHU Weishen. Parameter sensitivity analysis and optimizing for test programs [J]. Rock and Soil Mechanics, 1993, 14(1): 24-28.

[16]方军, 鲁世强, 王克鲁, 等. 0Cr21Ni6Mn9N不锈钢管管材数控弯曲截面畸变有限元分析 [J]. 塑性工程学报, 2013, 20(5): 71-76. FANG Jun, LU Shiqiang, WANG Kelu, et al. FE analysis of section distortion in numeriacl control bending of the 0Cr21Ni6Mn9N stainless steel tube [J]. Journal of Plasticity Engineering, 2013, 20(5): 71-76.

[17]FANG Jun, LU Shiqiang, WANG Kelu, et al. Effect of mandrel on cross-section quality in numerical control bending process of stainless steel 2169 small diameter tube [J]. Advances in Materials Science and Engineering, 2013, 2013: 1-9.

[18]刘树勋, 刘宪民, 刘蕤, 等. 0Cr21Ni6Mn9N奥氏体不锈钢的应变强化行为 [J]. 钢铁研究学报, 2005, 17(4): 40-44. LIU Shuxun, LIU Xianmin, LIU Rui, et al. Work-hardening behavior of 0Cr21Ni6Mn9N austenitic stainless steel [J]. Journal of Iron and Steel Research, 2005, 17(4): 40-44.

[19]李恒. 多模具约束下薄壁管数控弯曲成形过程失稳起皱行为研究 [D]. 西安: 西北工业大学, 2007.

[20]王振华, 田野, 张龙. 不锈钢管力学性能的拉伸试验 [J]. 塑性工程学报, 2012, 19(2): 56-59. WANG Zhenghua, TIAN Ye, ZHANG Long. Tensile test and study on the mechanical properties of stainless steel tubes [J]. Journal of Plasticity Engineering, 2012, 19(2): 56-59.

(编辑 赵炜 葛赵青)

Sensitivity Analysis of Springback to Material Parameters in High Strength 21-6-9 Stainless Steel Tube NC Bending

FANG Jun1,LU Shiqiang2,WANG Kelu2,TANG Jinxing2,YAO Zhengjun1

(1. Institute of Materials Science and Technology, Nanjing University of Aeronautics and Astronautics, Nanjing 211106, China; 2. School of Aeronautical Manufacturing Engineering, Nanchang Hangkong University, Nanchang 330063, China)

To investigate the effects of the material parameters variation on springback of high strength 21-6-9 stainless steel tube in NC bending, a sensitivity analysis model of the springback is established by combining the multi-parameter sensitivity analysis method and the finite element model of whole bend-springback process, and the sensitivities of springback to the material parameters are analyzed with the proposed model. The results show that the sensitivity of springback radius to material parameters is greater than that of springback angle. The most effective parameter on the springback is the strength coefficient, followed are elastic modulus, yield stress, strain hardening exponent, and Poisson’s ratio. The sensitive factors of springback angle and springback radius to the material parameters are obtained, and the relative errors of springback angle and springback radius caused by the 15% error between input value and actual value of the material parameters are also obtained. The research results may play an important role in optimizing test scheme and improving the ability of bent tube springback prediction.

21-6-9 high strength stainless steel tube; material parameters; springback; sensitivity analysis; finite element model

2014-08-21。 作者简介:方军(1984—),男,博士生;鲁世强(通信作者),男,教授,博士生导师。 基金项目:国家自然科学基金资助项目(51164030)。

时间: 2014-12-30

网络出版地址: http:∥www.cnki.net/kcms/detail/61.1069.T.20141230.0823.003.html

10.7652/xjtuxb201503021

TG386

A

0253-987X(2015)03-0136-07