动叶约化中心位置对涡轮非定常气动计算的影响

杨 杰，宋友富，熊清勇，杨伟平

(1.中国航发湖南动力机械研究所，湖南株洲 412002；2.中小型航空发动机叶轮机械湖南省重点实验室，湖南株洲 412002)

1 引言

涡轮内部流场本质是非定常的[1]。通过数值模拟获取涡轮内部时间精确流场最直接最精确的方法，是对涡轮流场进行全周模拟[2-3]，但此方法会花费巨大的计算资源。为减少计算资源开销，通常采用通道裁剪技术对涡轮内部流动进行非定常计算，且主要有三种方法[4]：时间周期性方法，时间倾斜方法和叶片数约化方法。

时间周期性方法由Erdos[5]提出，并由He[6]进一步发展。这种方法认为叶轮机中的流动在时间上存在周期性，故存储计算域周向边界的流动解作为下一个流动周期的边界条件。时间倾斜方法由Giles[7]提出，通过对欧拉/N-S方程进行时空变换、转-静叶排中采用不同的时间步长，以保证转静交接面两侧具有不同周向周期性的周期性边界条件能够使用。叶片数约化方法[8]由Rai提出，是通过对叶型进行缩放以调整叶片数，使多级叶轮机的各排叶片数成简单整数比例，然后充分利用叶轮机内部流动的周向周期性进行通道裁剪，从而减少需要模拟的通道数，减少计算量。前2 种方法需要作复杂的数学变换，实现难度较大。而叶片数约化方法的计算原理相对简单，实现起来相对容易，因此应用最为广泛。如Clark 等[9]对1.5 级跨声速涡轮进行了实验测量和不同约化形式的非定常数值模拟，研究了约化形式对叶片上非定常气动载荷数值计算结果的影响；May⁃orca等[10]对1级高负荷轴流压气机进行了数值计算，其结果表明，对于1 阶谐波激励，约化程度越大，预测精度越低；Hosseini等[11]对1级高负荷跨声速单级涡轮进行了数值计算，表明静子的气动力、低阶振型受约化的影响大；王远刚等[12]对1 级跨声速风扇进行了数值模拟，表明静叶约化形式对一、二阶谐波气动力有显著影响。

对于叶片数约化方法，有约化比和约化中心位置2个重要因素需要考虑。约化比即约化前后叶片数之比，约化中心位置即叶型缩放的基点。约化中心位置的选择是采用约化方法进行涡轮非定常气动计算过程中必须考虑的问题。采用不同的约化中心位置(如以叶片前缘或以叶片尾缘为约化中心位置)对非定常计算结果必然会造成不同的影响，对这种影响规律进行深入研究，可以指导采用约化方法的涡轮非定常气动计算。目前，关于约化中心位置相关的研究还未见公开报道。

本文针对单级涡轮的动叶约化，就动叶约化中心位置对涡轮内部流动非定常计算结果的影响规律开展了研究，总结出了可指导采用动叶约化方法进行涡轮非定常气动计算的结论。

2 研究方法

2.1 研究对象

研究对象为某发动机的单级高压涡轮。原涡轮静叶与动叶的叶片数分别为23、41。研究中，将动叶叶片数由41约化成46。约化时，保证动叶稠度不变，对叶型进行缩放，缩放中心位置分别选在动叶前缘点和几何中心，这样产生2 个约化中心位置不同的动叶约化涡轮，分别记为RQY、RZX，原涡轮记为RNO，见图1。

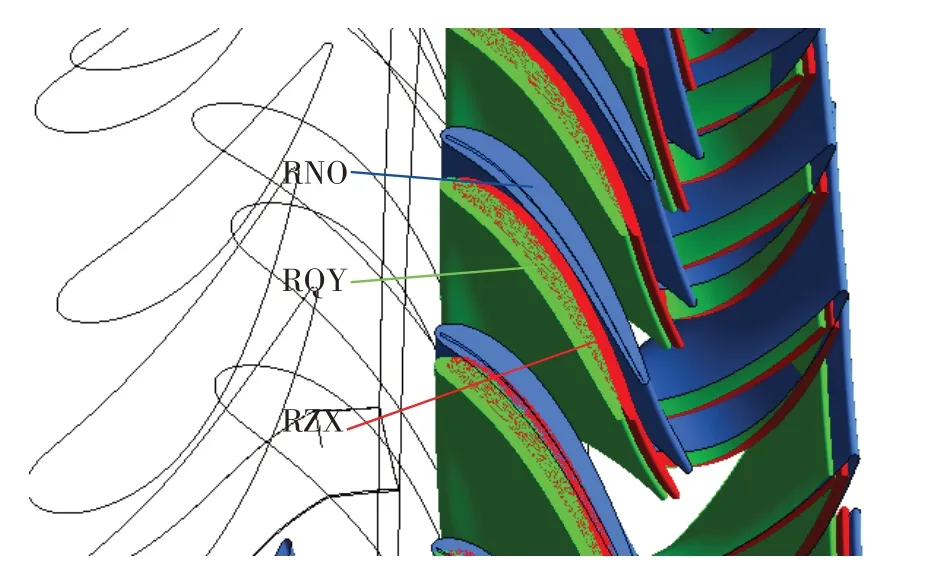
图1 动叶约化算例Fig.1 The rotor scaling cases

2.2 数值方法

流场的定常和非定常模拟通过采用商用软件CFX求解定常和非定常雷诺平均方程来实现。其中湍流的模拟采用带有自动壁面处理功能的剪切应力输运模型(SST 模型)。N-S 方程和湍流输运方程的对流项的离散均采用高阶格式，时间项的离散采用二阶向后欧拉格式，扩散项和压力梯度项的离散均通过采用形状函数(shape functions)计算空间导数来实现。非定常计算时，时间步长取1.0倍动叶通过周期(即转子转过1 个动叶通道的时间)的1/30。非定常计算进行了约100 个动叶通过周期后，得到了流场的收敛解。

2.3 计算模型

计算网格(图2)采用商用软件TurboGrid 生成。定常和非定常计算采用相同的网格和计算域。约化算例RXZ与RQY计算域含1个静叶通道和2个动叶通道，计算域总网格量约为200 万。非约化算例RNO 计算域含23 个导叶通道和41 个动叶通道，计算域总网格量约为4100万。各算例中，叶片及上下流道表面Y+值不超过5。动叶叶尖间隙内有15层网格。计算域进口位置距离第1 级静叶前缘约1.0 倍第1 级静叶叶中处轴向弦长；计算域出口位置距离第2级动叶尾缘约为1.5倍第2级动叶叶中处轴向弦长。

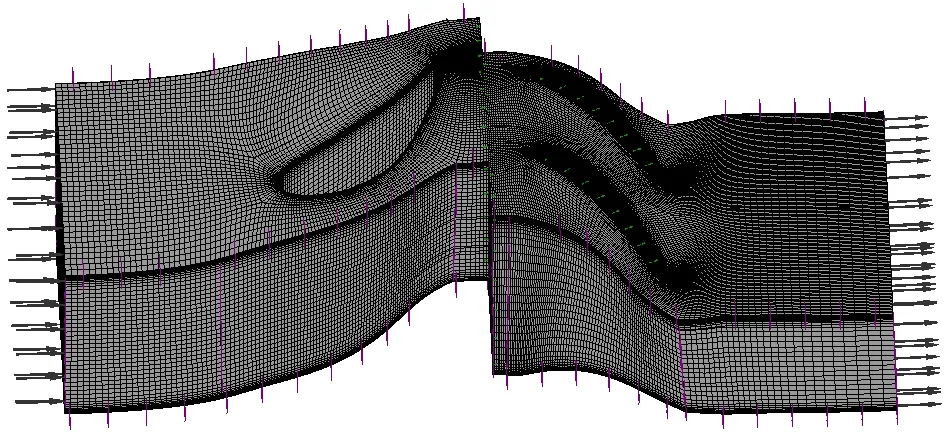
图2 计算网格Fig.2 Computation mesh

计算域进口给定总温、总压、进气方向和来流湍流度，出口给定平均静压。计算域展向两侧及叶片表面给定无滑移壁面边界条件，周向两侧设置为周期性边界。静子区域与转子区域的交接面在非定常计算时采用滑移面处理方式，在为获取非定常计算所需初场的定常计算中采用固结转子处理方式。

3 研究结果

对3个算例RZX、RQY、RNO的非定常计算结果进行分析。

3.1 性能与气动参数分析

表1给出了非约化算例RNO包括膨胀比、效率、流量、功率等在内的性能与气动参数的非定常时均值计算结果，及动叶中心约化算例RZX、动叶前缘约化算例RQY 的性能与气动参数非定常时均值计算结果相对于算例RNO 的变化。各算例的质量流量和功率以算例RNO作为基准进行无量纲化，称为相对质量流量和相对功率。除角度外，算例RZX(或RQY)相对于算例RNO的性能参数的差异定义为，算例RZX(或RQY)与算例RNO 之差与算例RNO 的比值；角度的差异定义为，算例RZX(或RQY)与算例RNO 之差。可见，2 个约化算例的各个性能与气动参数的时均计算结果与非约化算例RNO 的计算结果相差较小，仅算例RZX的静子能量损失系数的差异超过0.50%，而流量的差异不超过0.20%，效率的差异不超过0.10%。2个约化算例相比，两者的时均计算结果也相当，差异较小。这表明采用动叶约化方法进行非定常计算时，动叶约化位置的选择对于涡轮性能与气动参数的时均结果影响很小，几乎可忽略。

表1 涡轮性能与气动参数的非定常时均计算结果Table 1 Unsteady time-averaged computation results of the turbine performance and aerodynamic parameters

事实上，动叶约化时，若选取动叶前缘点为约化中心位置，则动叶尾缘位置会轴向移动，算例RQY由于动叶约化时叶型缩小，故动叶尾缘前移；若选取动叶几何中心为约化中心位置，则动叶前缘与尾缘会沿相反的方向沿轴向移动，算例RZX动叶前缘后移、动叶尾缘前移。本文算例中，动叶叶尖处的流道是平通道(结构上的原因，燃气涡轮动叶处为平通道是常见现象)，故动叶尾缘移动对于动叶喉部面积几乎无影响，为此动叶约化中心位置选在动叶前缘点或动叶几何中心，对涡轮的性能与气动参数的时均计算结果影响不大。

表2 给出了3 个算例性能与气动参数的非定常相对标准差计算结果。可见，非约化算例的性能与气动参数的非定常相对标准差的量级基本上是在10-6到10-7，而2 个约化算例的非定常相对标准差的量级基本上在10-3到10-4，即约化算例的非定常波动比非约化算例的要高2到3个量级。

对于非约化算例，由于静叶与动叶叶片数不可约，故在动叶转动1个静叶通道的不同时刻，静叶与动叶的相对位置存在多相性，各个相对位置相位进行平均后，不同时间的平均相位差异会很小。而涡轮在每一时刻的性能与气动参数是由该时刻静叶与动叶之间的平均相位决定的，故性能与气动参数的非定常波动很小。

对于2 个约化算例，静叶与动叶的叶片数之比为1:2。在动叶旋转1个静叶通道的每个时刻，静叶与动叶的相对相位呈现规律的周期性变化，故涡轮的性能与气动参数也呈现周期性变化，从而比约化算例有更大的非定常波动。

算例RZX与算例RQY相比，前者涡轮性能与气动参数的波动更小，这和算例RZX动叶与静叶之间的转静干涉比算例RQY 的弱有关。由于算例RZX转静之间的轴向间隙更大，故其转静干涉更弱。

3.2 流场分析

3.2.1 导叶的压力波动

图3给出了3个算例静叶在5%、50%、95%展向位置的表面静压相对标准差分布。对于3 个算例，在根、中、尖3 个展向位置，静叶上压力非定常波动强的区域均在静叶60%弦长以后的后段。其中，算例RNO静叶上的压力波动最强，在静叶上的范围最大；算例RQY静叶上的压力波动幅度与算例RZX的基本相当，但前者略强。

对比不同展向位置，对于3个算例，不管约化与否，均是静叶上的压力波动在根、尖截面位置比在中截面位置强。对于算例RNO，在3个展向位置，静叶上有较强压力波动的范围为60%弦长以后。对于2个约化算例，在5%展向位置，静叶上有较强压力波动的范围与算例RNO 的相当，但略靠后；在50%展向位置，此范围为70%弦长以后；在95%展向位置，此范围为80%弦长以后。

静叶上的压力脉动是由动叶对静叶势扰动引起的。动叶约化后，动叶长度会变短，这会导致2个动叶约化算例动叶对静叶的势扰动减弱，而且由于算例RZX的动叶前缘还会后移，故算例RZX的势扰动比算例RQY的更弱。

3.2.2 动叶的压力波动

图4给出了3个算例动叶在5%、50%、95%展向位置的表面静压相对标准差分布。对于动叶表面的压力波动，由于分布规律复杂，3个算例的趋势对比不明显。事实上，动叶表面压力波动的影响因素很多，典型因素有静叶的势扰动、端壁边界层形成的二次流、上游静叶的尾迹等，不像静叶那样仅由动叶的势扰动引起。

图中显示，在5%与95%展向位置，动叶前段，算例RZX的压力波动最大，这是由于算例RZX的转静间距最大，级间边界层发展形成的二次流最强，二次流与上游静叶的势扰动相互干涉，从而造成压力波动最强；动叶后段，算例RNO的压力波动最强，算例RQY 的次之，算例RZX 的最弱，这与边界层发展形成的二次流强弱及尾迹的耗散有关。算例RNO的动叶长度最大，到动叶后段时端壁边界层二次流最强，从而其动叶后段的压力波动最强。算例RZX不仅转静间距最大、尾迹的级间耗散最大，而且动叶尾缘位置相对算例RQY靠后，故上游尾迹在动叶中的耗散更大，动叶后段的压力波动最弱。

3.2.3 二次流分析

图5给出了动叶进口位置3个算例瞬时轴向速度环量云图的对比。图中显示，算例RZX 与算例RQY相比，前者上下端壁处动叶前的轴向速度环量更大，即上下端壁处的二次流更强。这导致了3.2.2节动叶前缘处压力波动算例RZX的最大。

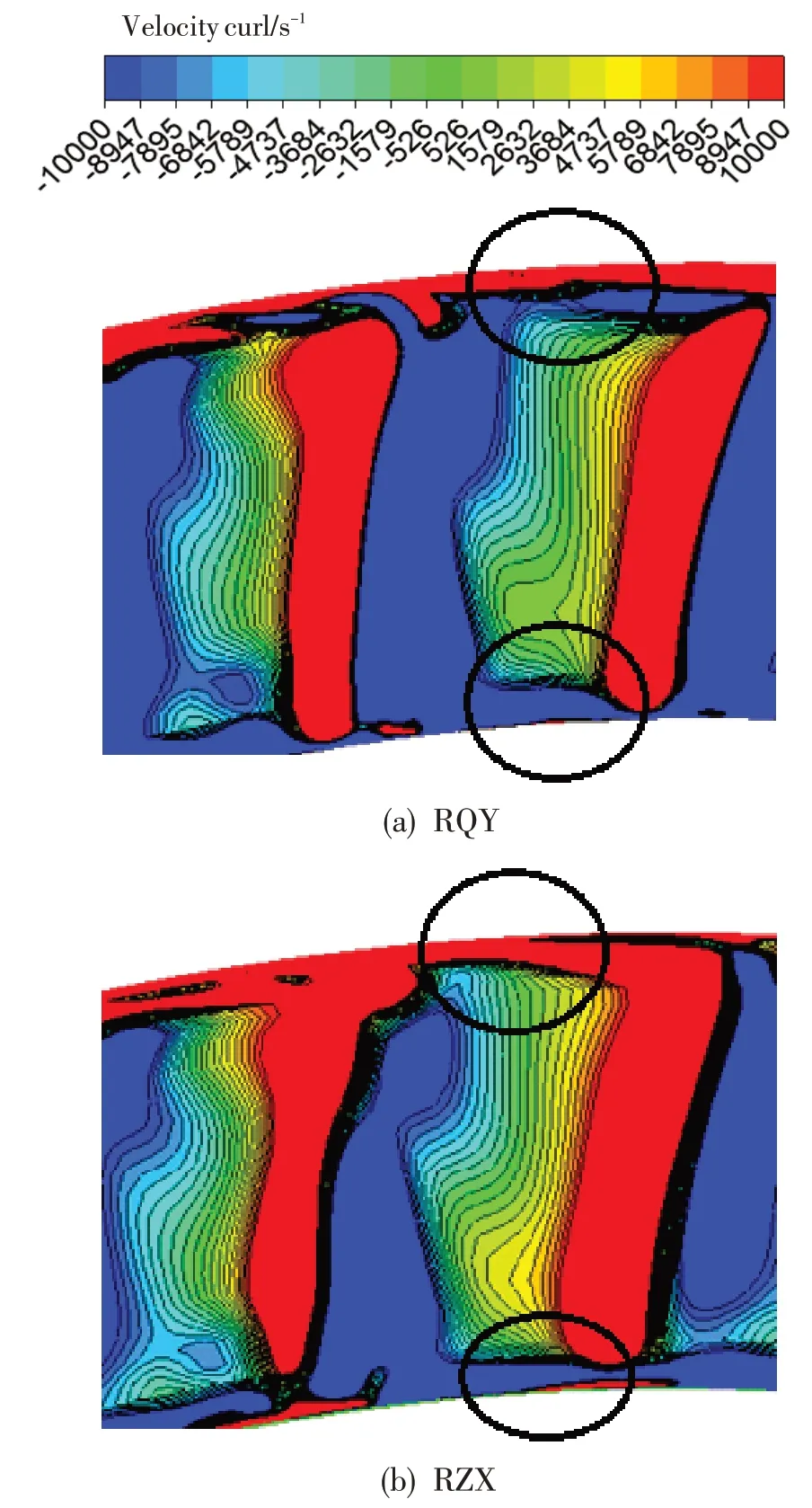
图5 动叶进口瞬时轴向速度环量云图Fig.5 The transient streamwise velocity curl contour at the rotor inlet

图6给出了动叶出口位置3个算例时均流向涡量云图的对比。图中显示，3个算例中，算例RNO下端壁通道涡、上端壁涡及叶中通道涡均最强；算例RZX下端壁通道涡及叶中通道涡比算例RQY的强，但其上壁面涡比算例RQY的弱。

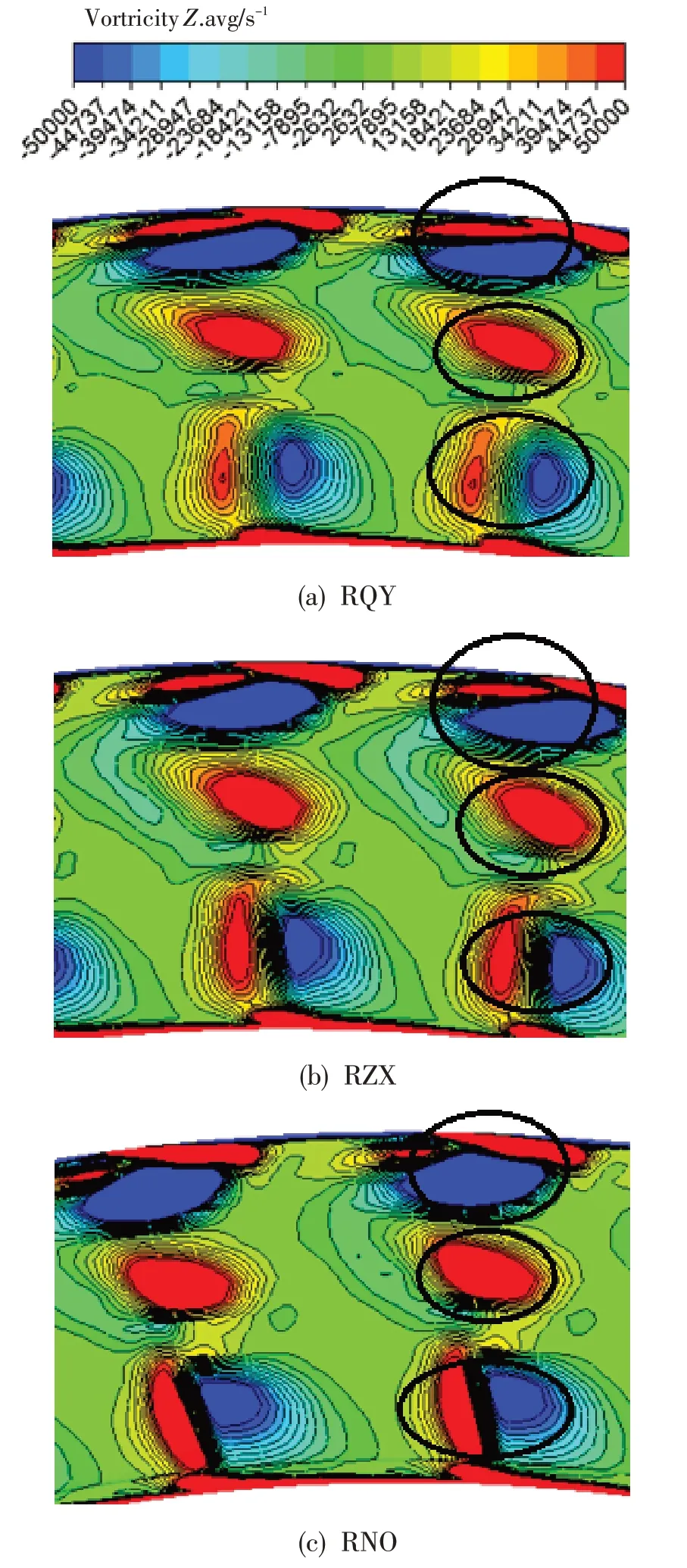
图6 动叶出口时均流向涡量云图Fig.6 The time-averaged streamwise vorticity contour at the rotor outlet

通道涡的强弱与边界层的发展有关。由于算例RNO叶片最长，故上下端壁及叶片中部的边界层发展最充分，通道涡最强。算例RZX与算例RQY相比，动叶尾缘更靠后，故其下端壁及叶中的边界层发展更充分，通道涡更强。而上壁面涡的强弱还受叶尖间隙流的影响，算例RZX 与算例RQY 相比，其尾缘更靠近下游，叶尖间隙的负荷更小，叶尖间隙流相对较弱，从而造成上壁面涡的强度较弱。

3.2.4 尾迹分析

图7给出了5%展向位置3个算例瞬时湍动能云图的对比。3 个算例中，算例RNO 动叶通道中的上游尾迹强度最强，算例RQY 的次之，算例RZX 的最弱。

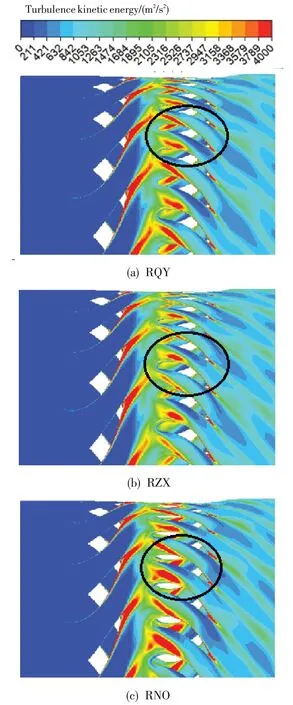
图7 5%展向位置瞬时湍动能云图Fig.7 The transient turbulence kinetic energy contour at the 5%spanwise position

动叶通道中上游尾迹的强弱与尾迹的耗散有关。由于算例RZX 动叶前缘后移，其转静间距最大，故上游尾迹在转静间隙中的耗散最多，到达动叶进口时最弱。与算例RQY 相比，算例RNO 的上游尾迹在不同动叶通道中的耗散不同频，故其尾迹强度在动叶通道中有强有弱，但总体上比同频耗散的算例RQY的强。

4 结论

对单级涡轮非定常流动计算采用不同的动叶约化中心位置(动叶前缘点与动叶中心)对于计算结果的影响开展了研究，得到如下结论：

(1)动叶通道的平整性，使得2 种动叶约化方式对涡轮性能与气动参数的时均值影响极小，影响的量级不超过0.50%。2 种约化方式对涡轮性能与气动参数的波动影响在同一数量级(动叶中心约化方式更小)，比不约化时低2到3个数量级。

(2)2 种动叶约化方式改变了势扰动的强弱，导致静叶上的压力波动均比动叶不约化时的小，且动叶中心约化方式比动叶前缘约化方式的略小。2种动叶约化方式改变了二次流及尾迹耗散的强弱，导致动叶上的压力波动呈现复杂的变化规律。

(3)动叶中心约化方式增大了轴向间距，从而使得其动叶进口的上下端壁二次流最强。2种约化方式约化后动叶均变短，从而导致其端壁边界层的发展均没有不约化时充分，故动叶出口端壁处的二次流均比不约化时弱。

(4)2种动叶约化方式对转静轴向间距及叶片位置造成影响，从而影响到上游静叶尾迹在动叶通道中的耗散，进而导致不约化时动叶通道中的上游尾迹强度最强，动叶前缘约化时次之，动叶中心约化时最弱。

(5)动叶前缘约化方式和动叶尾缘约化方式对涡轮性能与流动的影响量级均较小，其中前缘约化方式的影响更小。非定常计算时，2 种优化方式都可选用，且优先选用前缘约化方式。