镍基合金K438高温弹塑性变形行为与本构模型研究

艾 兴，李 坚，孙 力，胡绪腾，米 栋，孟卫华，张志佾

(1.中国航发湖南动力机械研究所，湖南株洲412002，2.南京航空航天大学，南京 210016)

1 引言

K438 铸造镍基高温合金是我国研制的耐热腐蚀性能最好的铸造镍基高温合金之一。该合金的成分、性能与国外IN738合金的类似，除拥有优秀的耐热腐蚀性能外，还拥有中等水平的高温强度，以及良好的组织稳定性，被广泛选作航空发动机涡轮叶片等热端部件材料[1]。国外学者对IN738 合金组织成份和性能开展了较多研究，国内对该材料力学性能的研究有限。

某涡轴发动机动力涡轮叶片(以下简称涡轮叶片)工作时处于高温复杂应力状态，为准确预测其断裂转速，需对其变形失效行为进行精准描述。为此，针对动力涡轮叶片材料K438，开展了光滑和缺口试样的准静态拉伸试验，分析获取了材料的拉伸失效模式及其应力-应变关系曲线，并以此为基础构建了该材料的本构模型，同时验证了模型的有效性和适用性。研究成果为K438 材料在结构件上的应用提供了理论基础。

2 本构模型构建

2.1 K438高温拉伸试验

基于国家标准GB/T 228.1-2010[2]，根据叶片毛坯具体尺寸设计的K438 材料光滑试样高温拉伸试验方案如表1所示，光滑试样图纸如图1所示。

表1 K438材料光滑试样拉伸试验方案Table 1 Tensile test scheme for smooth specimen of K438 material

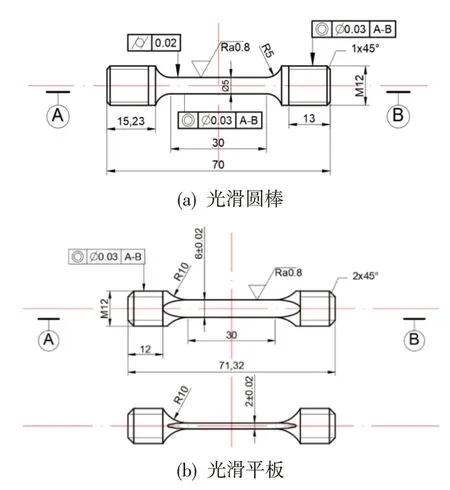
图1 K438光滑试样图纸Fig.1 K438 smooth specimen drawing

图2为K438材料光滑试样700℃高温下的拉伸工程应力-应变曲线，其中未特别标注批次的试样均为第二批材料。分析试验结果可以看出，两批材料的高温性能存在差异，抗拉强度、屈服强度均是第二批材料的较高；同一批次不同形式的光滑试样(平板或圆棒)性能相近，无明显差异。

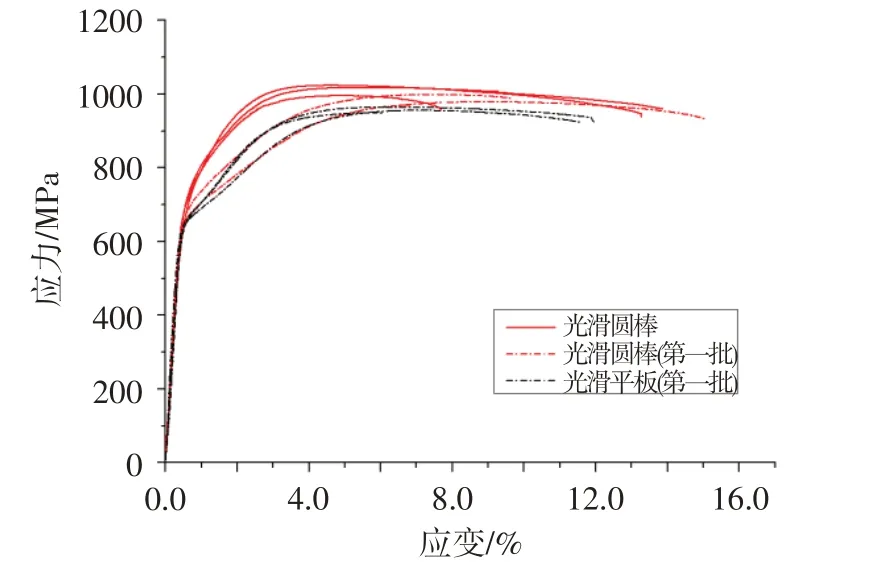
图2 光滑试样高温拉伸试验结果(700℃)Fig.2 Tensile test results of smooth specimens under high temperature(700℃)

2.2 K438本构模型构建

K438 属于各向同性材料，为方便工程应用，采用各向同性多线性本构模型对材料行为进行描述。多线性本构模型采用分段的线性方程来描述材料的应力-应变曲线：

方程中：(σ1,ε1)、(σ2,ε2)、(σ3,ε3)……(σn,εn)为本构模型分段端点，可直接对材料力-真应变曲线进行描点拟合获得，T1、T2、T3……Tn为各段斜率。通常情况下，多线性本构模型的第1段为材料弹性段，斜率为弹性模量E。光滑试样在其工程应力-应变最高点发生颈缩。在光滑试样拉伸变形发生颈缩后，即超过工程应力-应变最高点后，工程应力-应变无法再通过转换公式转换为真应力-真应变曲线，故将材料变形行为处理为理想弹塑性，对应的真应力-真应变曲线斜率为0，即Tn=0。

考虑到材料本身性能的分散性较大，对光滑试样的高温拉伸结果的最高与最低曲线分别进行描点拟合得出本构，以期提高预测结果的准确性，描点拟合结果如图3 所示。可看出，多线性本构模型的描点合适，可以有效描述K438真应力-真应变曲线特征。高温上、下限本构的屈服强度相似，进入塑性后的硬化行为相差较大。上限本构在屈服后曲线斜率呈较为平滑的衰减，而下限本构更接近于双线性模型，屈服后曲线斜率快速衰减至某一确定值附近。

图3 K438高温拉伸真实应力-真实应变曲线和多线性本构模型的描点拟合(700℃)Fig.3 Real tensile stress of K438 under high temperature:tracing point fitting of real stress curve and multi-linear constitutive model(700℃)

3 高温缺口特征件设计与试验

为实现对不同受载时实际涡轮叶片复杂多轴应力状态的模拟，根据毛坯实际尺寸，设计了3种试样类型：①缺口圆棒试样，为轴对称试样，其内部应力状态接近二维平面应力问题；②双边侧槽平板试样，接近于平面应变问题；③双边缺口平板试样，属于三维复杂应力问题。同时，缺口圆棒与双边缺口平板试样各设计2种应力集中系数(Kt)，双边侧槽平板试样设计1 种应力集中系数，共计5 种缺口特征件。K438 材料缺口特征件高温拉伸试验方案如表2 所示，缺口特征件图纸见图4。

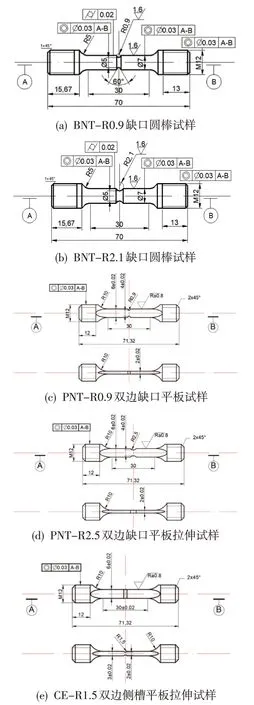
图4 K438缺口特征件拉伸试样图纸Fig.4 Drawings of K438 notched tensile specimen

表2 K438缺口特征件高温拉伸试验方案Table 2 Tensile test scheme of K438 notched specimens under high temperature

K438缺口特征件高温拉伸的工程应力-应变曲线如图5 所示。由图可以看出，随着应力集中系数的增大，缺口圆棒试样抗拉强度上升，但双边缺口平板试样的变化不大。对于相同应力集中系数的试样，缺口圆棒试样的抗拉强度高于双边缺口平板试样。对于双边侧槽平板试样，试验分散性较大，其抗拉强度均高于双边缺口平板试样。

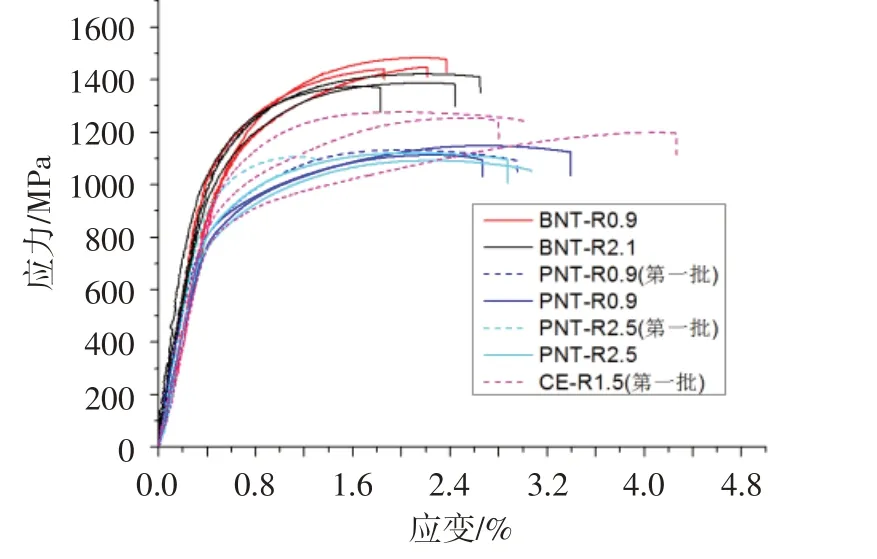
图5 K438缺口特征件拉伸结果(700℃)Fig.5 Tensile results of K438 notched specimens(700℃)

4 K438缺口特征件有限元预测与修正

在拥有大量复杂应力状态的缺口特征件高温拉伸试验数据后，即可使用已建立的本构模型对缺口特征件的拉伸响应曲线进行预测，并与试验结果进进行对比，检验本构模型与失效准则的适用性。通过建立上、下限本构模型，给出材料性能的上、下限预测曲线，排除试验数据分散性的影响；同时，采用基于Crockroft-Latham 韧性断裂模型[3]建立的K438失效准则，对有限元预测结果进行修正。

4.1 K438缺口特征件有限元模型

K438 材料缺口特征件有限元模型如图6 所示。在保证准确性的前提下，仅建立引伸计标距段内的模型。其中，缺口圆棒有限元模型为轴对称模型，双边缺口平板和双边侧槽平板有限元模型为三维模型。

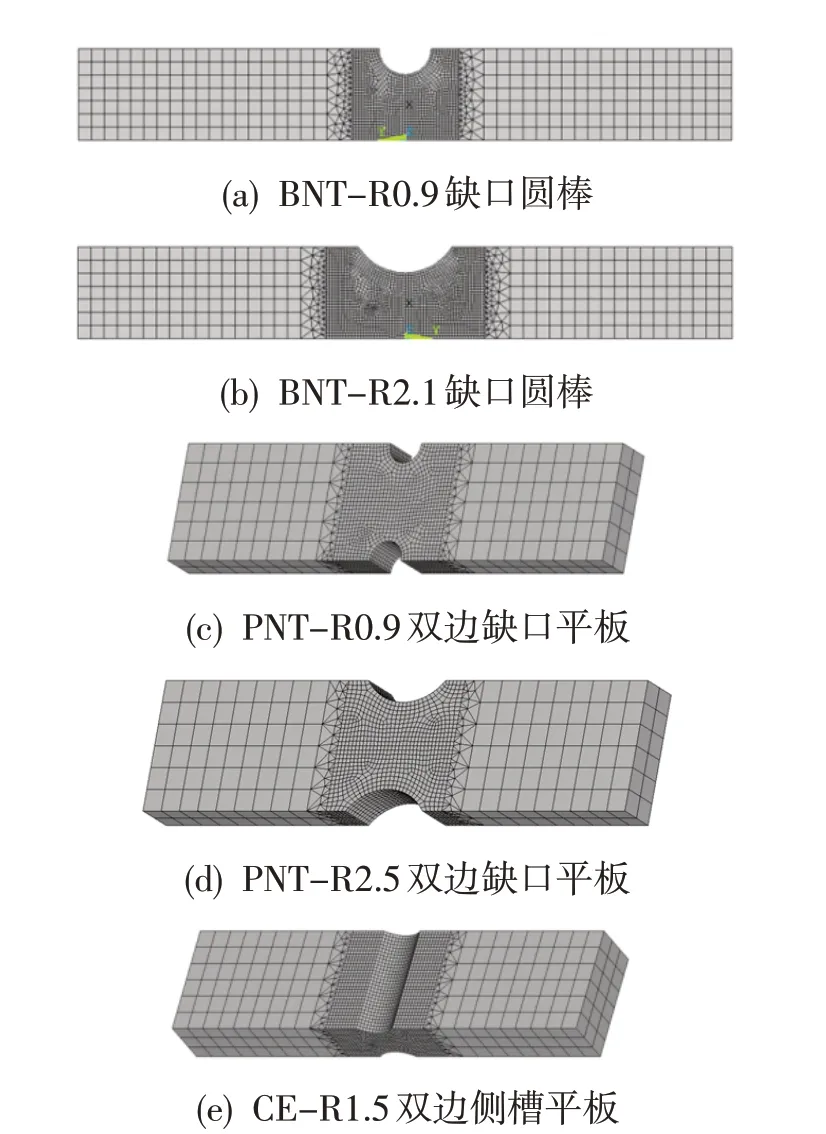
图6 K438缺口特征件有限元模型Fig.6 K438 notched specimen FEM model

4.2 本构模型的有限元预测及修正

由于光滑试样拉伸至工程应力-应变曲线最高点(失稳点)附近时，因试样发生颈缩而不再适用于真实应力-真实应变转化公式。故采用多线性本构模型对光滑试样真应力-真应变曲线进行拟合时，仅对失稳点前曲线转化的真实应力-真实应变曲线进行描点，假设材料在失稳点后处于理想塑性。但真实材料在失稳点后仍会继续硬化，失稳点后理想塑性假设会导致缺口特征件预测拉伸响应曲线低于试验结果(预测曲线还未接近试验曲线的最高点就开始迅速下降，如图7 所示)，故对多线性本构模型进行外延修正，并假设材料在失稳点后，以失稳点处的斜率继续硬化。

图7 K438本构模型预测结果与试验结果的对比(700℃)Fig.7 Comparison between K438 constitutive model prediction results and test results(700℃)

为更直观地反映实际数值计算所用外延上、下限本构模型与光滑试样拉伸试验数据之间的关系，将外延后多线性本构通过真应力-真应变转化公式转换为工程应力-应变曲线与试验曲线进行对比，见图8。可以看到，外延后的上、下限本构可以有效包裹光滑试样试验结果。

图8 上、下限本构模型与试验数据的对比(700℃)Fig.8 Comparison between upper and lower limit constitutive model and test data(700℃)

采用带有外延的K438 高温多线性本构对缺口特征件高温拉伸试验结果进行预测，结果如图9 所示。将预测所得极限强度与试验平均极限强度数据进行汇总，结果如表3 所示。分析图9 与表3 可知，含外延的高温上、下限本构能很好地囊括高温试验件的分散区间，试验曲线基本被包含在上、下限本构预测结果之间；从极限强度方面看，预测误差均在3.00%左右，最大也仅-5.02%。这说明构建的高温上、下限本构模型可以有效地描述K438高温性能。

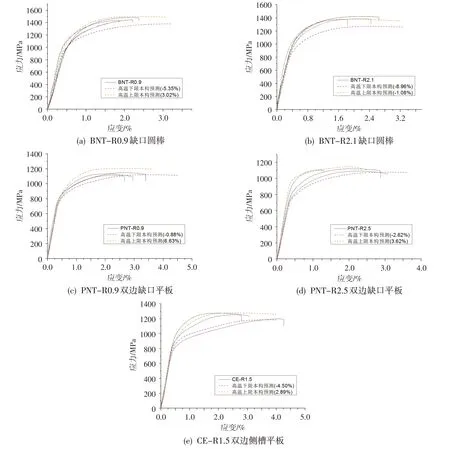
图9 K438缺口特征件拉伸结果与有限元预测结果的对比(700℃)Fig.9 Comparison between K438 notched tensile results and FEM prediction results(700℃)

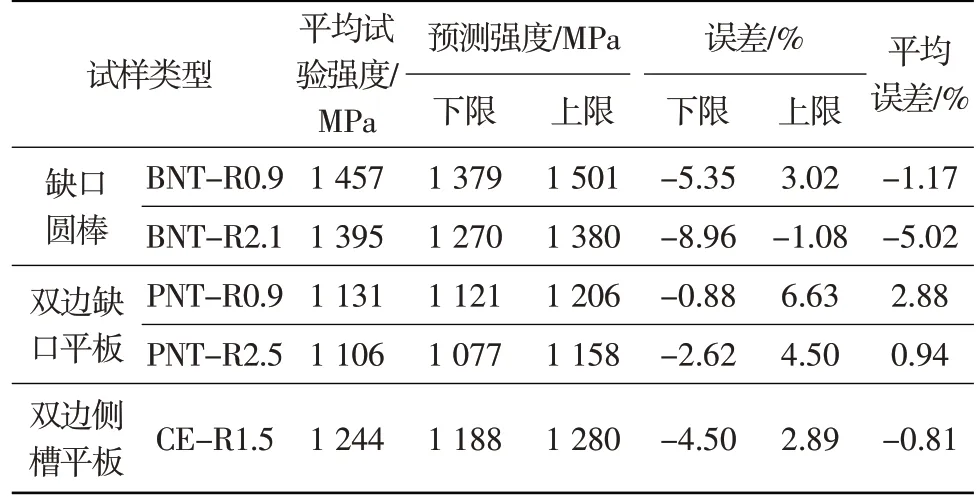
表3 K438缺口特征件试验极限强度与有限元预测结果的对比(700℃)Table 3 Comparison between K438 notched UTC results and FEM prediction results(700℃)

4.3 断裂模型建立与预测结果修正

具有一定延性的金属断裂形式大多属于韧性断裂，即断裂是由孔洞的聚合和生长引起的。这些孔洞是材料中因位错堆积、第二相粒子或其他缺陷而产生的，在金属塑性变形的作用下能够长大，直至一定数量的孔洞聚合起来形成裂纹[4-6]。很多学者已根据其研究成果提出了自己的断裂准则[7-10]，其中Freu⁃denthal失效准则[9]、Oyane准则[10]及Crockroft-Latham断裂准则[11]等被广泛应用。本文针对K438材料，选取Crockroft-Latham 韧性断裂模型，提出了适用于K438材料高温性能的断裂准则。

根据Crockroft-Latham模型，第一主应力是引起断裂的主要原因，在一定的应变速率和温度下，当第一拉伸主应力沿应变路径的积分值达到损伤阈值时，材料就发生了失效断裂。Crockroft-Latham断裂模型的具体形式如下：

由于分别针对最高和最低光滑拉伸试验曲线拟合了上、下限弹塑性本构模型，因此需针对高温上、下限本构分别计算C1。基于已有的有限元计算结果，C1的具体计算方法为：

(1)从现有缺口件的极限强度预测结果中选择预测误差最小的一条曲线作为基准。

(2)在ANSYS时间后处理器中，读取缺口件模型中缺口根部的最外侧结点的最大主应力与Mises等效应力及Mises 等效塑性应变，并计算最大主应力和Mises等效应力的比值。

(3)进行数值积分，计算达到极限载荷时的C1，并将其作为该本构下的阈值。

(4)重复上述步骤，对其他曲线进行数值积分，获取达到C1时的时间步。

(5)判断积分值达到C1时的时间步是否越过最大载荷对应的时间步。如是，则预测的最大载荷即为极限预测载荷；如否，则达到阈值时刻的载荷即为极限预测载荷。

经过上述步骤获取的C1结果如表4所示。采用相应的C1对所有预测极限载荷进行修正，获得修正后的极限强度与误差如表5所示。

表4 K438各本构对应的失效阈值Table 4 K438 constitutive model related failure threshold value

表5 Crockroft-Latham断裂准则修正结果(700℃)Table 5 Corrective results of Crockroft-Latham rupture(700℃)

表5中灰底数据为判断C1的基准预测曲线对应的极限强度，表中箭头标识出采用断裂准则修正后的数据变化趋势。分析表5 可以看出，对于下限本构预测曲线，除BNT-R0.9缺口圆棒试样外，其余试样采用断裂准则判断失效时的载荷时间步均在预测曲线的最大载荷点对应的时间步之后，故预测极限强度不变，预测误差并无改善。对于上限本构预测曲线，部分试样采用断裂准则判断失效时的载荷时间步在预测曲线的最大载荷点对应的时间步之前，说明这些拉伸预测曲线并不能到达曲线的最高点，预测极限抗拉强度有所下降；由于原上限本构预测极限强度普遍偏高，因而修正后的预测误差有所下降。

综上所述，采用Crockroft-Latham断裂准则对于K438高温失效行为具有较好的适用性，文中确定的断裂模型参数可合理地描述K438高温断裂行为，有效修正缺口特征件极限强度预测结果。

5 K438缺口件失效行为分析

为进一步分析K438缺口特征件失效行为，绘制了室温与高温环境下，应力集中系数与名义屈服强度、名义抗拉强度的关系，见图10、图11。分析可知：①室温环境下(黑色填充)，随着应力集中系数的增大，双边缺口平板试样和缺口圆棒试样的屈服强度均呈现上升的趋势，抗拉强度均呈现微微下降的趋势。说明室温下随着应力集中系数的增大，缺口特征件的名义屈服强度上升，但极限承载能力下降。②700℃高温下，随着应力集中系数的增大，双边缺口平板试样的名义屈服强度呈现下降的趋势，抗拉强度呈现上升的趋势；而圆棒缺口件的屈服强度变化规律与抗拉强度变化规律一致，均呈现上升的趋势。这说明，屈服强度与抗拉强度变化规律不仅与构件类型(主要是危险截面大小)相关，而且还受温度与应力集中系数影响。③应力集中系数相同时，700℃高温下缺口特征件的名义屈服强度均低于室温下名义屈服强度，但其抗拉强度的变化规律并不一致，缺口平板件（包括双边缺口平板和双边侧槽平板）在高温下的的抗拉强度相较于室温下的有所下降，缺口圆棒件的却有所上升。

图10 应力集中系数与屈服强度的关系图Fig.10 Relationship between stress concentration factor and yield strength

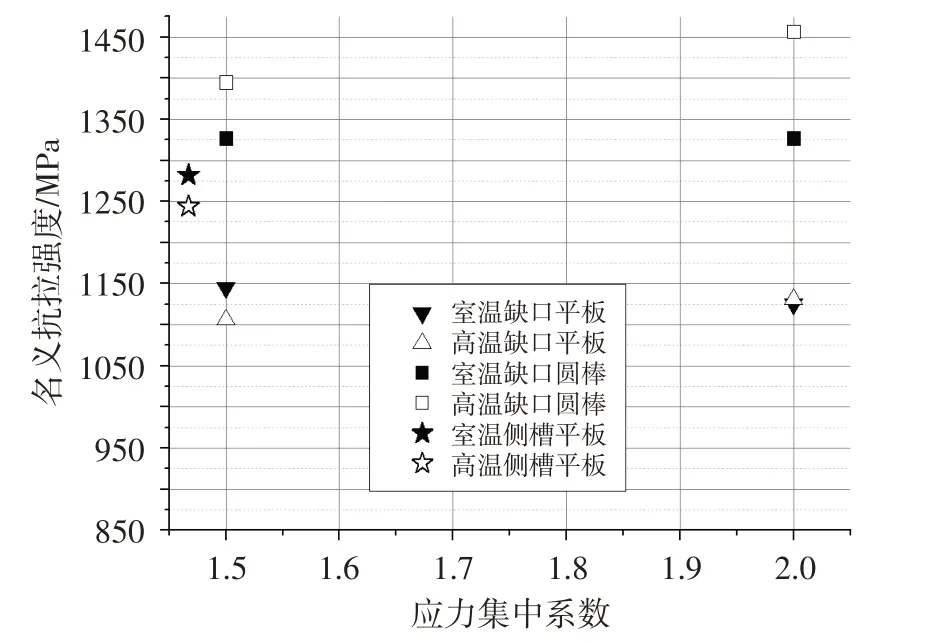
图11 应力集中系数与抗拉强度的关系图Fig.11 Relationship between stress concentration factor and tensile strength

6 结论

通过K438 光滑试样和缺口特征件的高温准静态拉伸试验，分析了K438缺口特征件的拉伸试验失效行为。根据试验结果，建立了K438 高温下外延上、下限本构模型，对K438 缺口特征件高温下拉伸变形行为进行了预测。进一步确定了基于Crock⁃roft-Latham断裂模型下的K438高温断裂模型参数，对预测结果进行了修正。结果表明：

(1)采用上、下限本构来表征K438材料性能的分散范围进而降低预测误差的方法行之有效，对K438缺口特征件极限强度的上、下限平均预测误差不超过5.02%。

(2)基于Crockroft-Latham 断裂模型建立的K438 高温断裂模型，能够很好地降低K438 上限本构的估计误差，但对下限本构偏低预测曲线基本无修正效果。

(3)K438 材料的失效行为受多方面影响，温度、应力集中以及几何形状均对材料的屈服强度与抗拉强度有一定影响，且影响规律不尽相同。