地铁车辆车轮轮缘厚度预警区间研究

宗志祥

（上海地铁维护保障有限公司 车辆分公司，上海 200235）

轮缘是车轮上的重要组成部分，使车轮安全可靠的通过曲线和道岔［1］。轮缘厚度作为车轮轮缘检修项目的关键参数之一，其作用主要在于防止车辆在运行过程中发生较大的横向运动，通过对轮缘厚度值的定期跟踪并确保在安全范围内，有助于抑制车辆的蛇行运动。

近年来，国内学者对车轮轮缘厚度进行了大量的研究。邬春晖［2］对动车和拖车旋修前的直径和轮缘厚度进行了对比，得出拖车磨耗速率大于动车磨耗速率的结论。方宇等［3］分析了上海地铁3号线轮缘厚度变化情况，认为随着车辆运行里程的增加，所有车轮的轮缘都存在一定的“虚增厚”现象。于春广等［4］对地铁线的4列车进行了车轮磨耗测试，通过对轮缘厚度值分析，发现有73%的轮对表现为右侧车轮轮缘厚度大于左侧车轮，轮缘存在严重偏磨现象。文永蓬等［1］将地铁车辆的轮缘厚度的检测值与轮缘厚度值进行比较，发现拖车的轮缘厚度增大情况更容易出现。以往的研究中，大多数都是将轮缘厚度的实际检测值与轮缘厚度允许范围或者是轮缘标准值进行对比分析，获得车轮的磨耗特性，并提出相应的建议。不可否认的是，在全国地铁车辆检修过程中，判断检测出的轮缘厚度值是否超限，主要的参考依据是商家给出的轮缘厚度范围以及轮缘厚度的标准值。但值得一提的是，地铁车辆在运行过程中，检测出轮缘厚度值超限时，车辆在这之前已经发生了一些超限运行，存在一定的安全隐患，因此，需要在车辆轮缘厚度值超限之前，给出轮缘厚度的预警值，进而规避安全隐患。

为此，论文根据上海地铁13号线车辆的车轮检测数据，利用正态分布函数对车轮轮缘厚度值进行描述，结合正态分布函数的特性、轮缘厚度的范围和轮缘厚度标准值，获得了地铁车辆车轮轮缘厚度的预警区间。

1 轮缘厚度计算方法和特性

为了减少车轮与钢轨的磨耗，上海地铁13号线1301号车辆车轮采用磨耗形踏面［5］，其磨耗形轮缘厚度的定义如图1所示。图1中，车轮直径的基准点D0距轮缘外侧70 mm，以D0为参考依据，往上10 mm的距离与轮缘内侧有一交点P，P点距轮缘外侧的水平距离为轮缘厚度。

图1 车轮轮缘厚度计算方法

车辆在运行的过程中，轮轨间的滚动摩擦必然导致车轮发生磨耗［6］，由于轮缘厚度值是以基线相对位置为测量值，受轮缘与踏面磨耗速率影响。一方面，当轮缘厚度值偏小时，这说明轮缘磨损速率大于踏面磨损速率，使得车轮与钢轨间的间隙过大，易发生横向移动，产生剧烈的蛇行运动，降低车辆的运行平稳性和乘坐舒适性；另一方面，当轮缘厚度值过大时，即发生“轮缘虚增高”现象，这意味着轮缘磨损速率小于踏面磨损速率，造成的结果是地铁车辆在运行通过曲线时，车轮与钢轨发生“卡死”现象，产生较大的异常转弯噪声，对周边居民的生活造成一定的影响。

2 正态分布与假设检验理论

2.1 正态分布

式中：μ为均值，σ为标准差，则称X服从以μ，σ为参数的正态分布，记为X～N（μ，σ2）。

正态变量X的分布函数为式（2）：

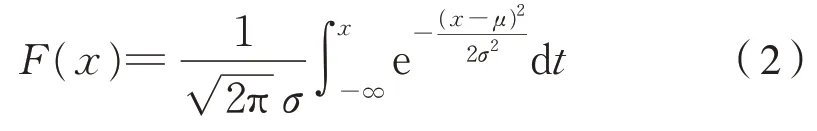
2.2 假设检验

下面需要对轮缘厚度总体样本服从正态分布的推断进行假设性检验，验证其假设的正确性。其正态分布假设性检验的流程如图2所示。

由图2可知，其具体步骤为：

图2 假设性检验流程图

（1）提出零假设和备择假设

零假设H0：X服从正态分布；

经研究表明，观察组中老年糖尿病合并脑梗塞患者检出率90.00%（阴性患者10例、百分比为10.00%；阳性患者90例、百分比为90.00%）高于对照组检出率80.00%，差异有统计学意义（P＜0.05）。

备择假设H1：X不服从正态分布。

（2）选择正态分布检验方法

鉴于不清楚轮缘厚度样本数值是否服从正态分 布，选 用 非 参 数 检 验K-S［9］（Kolmogorov-Smirnov test）检验对样本数值进行检验。

（3）选择检验的显著性水平α

显著性水平是数学界约定俗成的，通常取值有0.01，0.05，0.1这3个等级，在统计学中，通常把发生几率小于0.05的事件称之为“不可能事件”，因此，取显著性水平α为0.05。

（4）计算检验的p值

检验的p值是指在零假设条件成立下，检验统计量等于现实值的概率。p值越小，说明在零假设的前提下发生小概率事件，应该拒绝零假设。

（5）检验判断

比较p值和α值的大小，若p＜α，则拒绝零假设，若p＞α，则不能拒绝零假设，说明X服从正态分布。

3 轮缘厚度值预警区间

3.1 整车预警区间

根据上海地铁13号线的1301号车辆12个月的轮缘厚度检修测量数据，利用正态分布和假设检验理论进行分布拟合和假设检验，其整车车辆轮缘厚度分布拟合如图3所示，假设性检验表见表1。

由图3和表1可知，整车轮缘厚假设性检验的显著性水平为0.2，大于原先设定的0.05，说明不能拒绝零假设，因此可认为整车轮缘厚度的服从正态分布，记为：X～N（29.06，0.662）。

表1 轮缘厚度假设性检验

图3 整车轮缘厚度正态分布拟合曲线图

根据正态分布的“3σ”原则，可以获得整车轮缘厚度的取值区间为（μ-3σ，μ+3σ），即（27.08，31.04）。利用车轮轮缘厚度的范围26～33 mm、标准值32 mm、维修检测出来服从正态分布的轮缘厚度取值区间。获得整车的轮缘厚度的分布区间，如图4所示。

图4 整车轮缘厚度分布区间

由图4可知，整车车轮轮缘厚度值的正常区间为（27.08，32），预 警 区 间 为（26，27.08）和（32，33），其中，区间（26，27.08）为轮缘厚度磨耗过量区，区间（32，33）为“轮缘虚增高区”。

综上可知，获得车轮轮缘厚度的预警区间的步骤概括如下：

第一步：利用正态函数对车轮轮缘厚度实际检测值进行描述。

第二步：选用检验方法并对提出的统计推断进行了假设检验。若服从正态分布，则可进行下一步，若不服从正态分布，则事件结束。

第三步：结合正态分布函数的特性、轮缘厚度的允许范围和轮缘厚度标准值，最终获得地铁车辆整车车轮轮缘厚度的预警区间。

获得轮缘厚度预警区间流程如图5所示。

图5 获得轮缘厚度预警区间流程图

3.2 运行线路的影响

此外，地铁车辆运行不可避免的需要通过曲线段，带来的结果是左右车轮的磨耗特性存在一定的偏差，因此，需要对左右车轮的轮缘厚度进行分析研究。同样运用正态分布和与假设检验理论对左右车轮轮缘厚度进行描述，获得的拟合曲线如图6所示，则左右轮缘厚度服从的正态分布依次为：X左～N（29.22，0.592）、X右～N（28.90，0.692）。

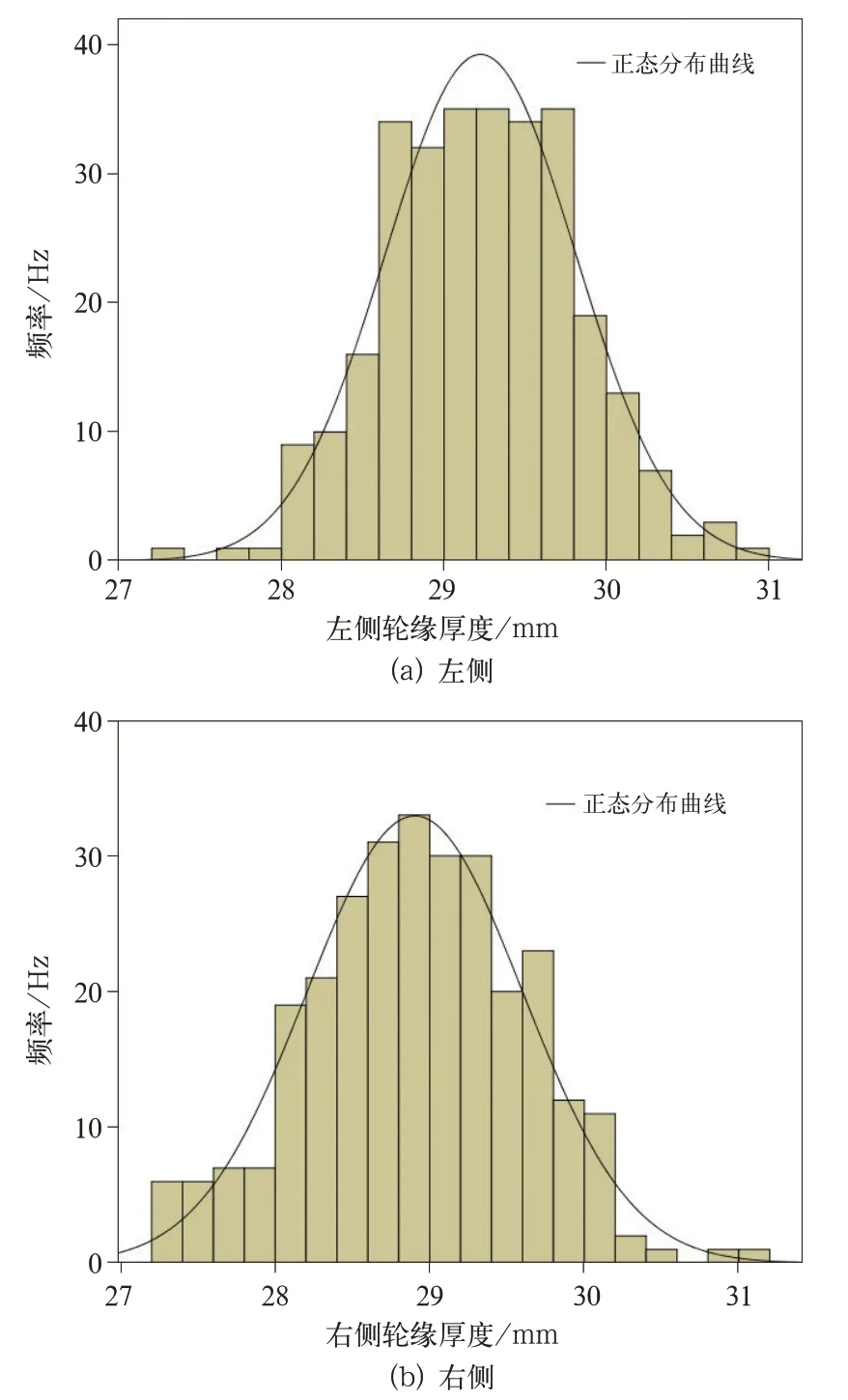
图6 左右轮缘厚度正态分布拟合曲线图

左右侧车轮轮缘厚度值区间分布见表2，左侧车轮轮缘厚度的均值29.22 mm，大于右侧的车轮轮缘厚度均值28.90 mm，这说明左侧的车轮轮缘磨耗要小于右侧的车轮轮缘磨耗，出现了偏磨现象，这是因为地铁车辆始终服役于固定的专用线路，建议在均衡修周期中调换左右轮，或者定期让车辆反向运行，减缓左右车轮的偏磨。此外，左右侧轮缘厚度预警值相比，左侧轮缘厚度值为27.45 mm开始预警，而右侧轮缘厚度值为26.83 mm才开始预警，这说明右侧轮缘厚度预警区间要大于左侧轮缘厚度预警区间，因此，不同侧的车轮磨耗出现偏差时，轮缘厚度预警区间需要特定设置。

表2 左右侧车轮轮缘厚度区间分布

3.3 运行里程的影响

值得一提的是，地铁车辆在服役过程中，随着运行里程的变化，其车轮的磨耗特性也会随之改变，为了探索不同里程下车轮轮缘厚度的规律，选取1301号车辆运行里程分别为410 233、440 249、493 663 km，运用正态分布和假设检验理论对运行不同里程的车轮轮缘厚度进行描述，获得的拟合曲线如图7所示，则3种不同运行里程的车轮轮缘厚度服从 的 正 态 分 布 依 次 为：X410233～N（28.80，0.672）、X440249～N（28.92，0.692）、X493663～N（29.42，0.652）。

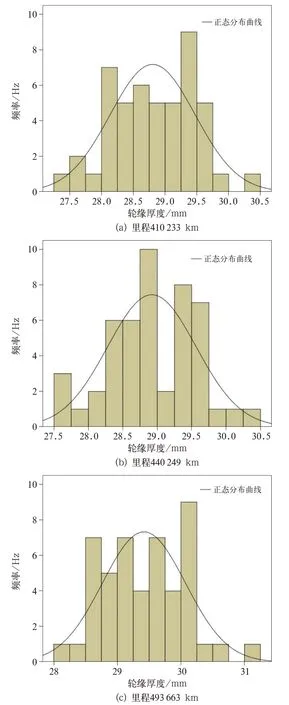
图7 不同里程轮缘厚度正态分布拟合曲线图

3种不同里程下地铁车辆车轮轮缘厚度值区间分布见表3，由表3可知，随着运行里程的增加，车轮轮缘厚度的均值也呈增大趋势，其各自的轮缘厚度预警区间也表现出很大的差异，为了进一步分析运行里程对预警区间的影响，定义ΔSW ew为车轮轮缘厚度预警区间的长度，长度计算公式为式（3）：

表3 不同里程的车轮轮缘厚度区间分布

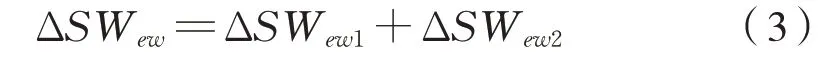
式中：ΔSW ew1为预警区间的第1个长度；ΔSW ew2为预警区间的第2个长度。

利用式（3）获得3种不同里程下地铁车辆车轮轮缘厚度预警区间的长度，如图8所示。由图8可知，随着地铁车辆运行里程的增加，车轮预警区间长度也随之增大，这意味着车辆运行里程越大，其车轮轮缘厚度预警区间范围增大，应更早地跟踪和检测轮缘厚度，避免发生过度磨耗超限运行，从而提高运行安全性。

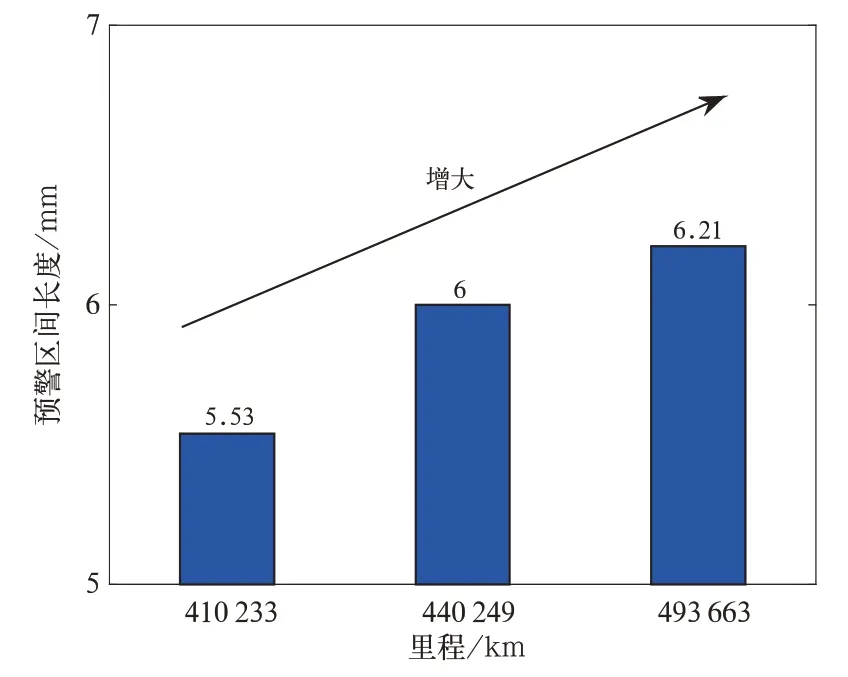
图8 运行里程对轮缘厚度预警区间长度的影响

4 总结

（1）利用正态分布函数对地铁车辆整车车轮轮缘厚度值进行了统计推断和假设检验，认为整车车轮轮缘厚度服从正态分布函数。结合正态分布函数特性、轮缘厚度范围和轮缘厚度标准值，获得了地铁车辆整车车轮轮缘厚度的预警区间。

（2）左右侧车轮存在偏磨现象，建议在均衡修周期中调换左右轮，或者定期让车辆反向运行，减缓左右车轮的偏磨。当不同侧的车轮磨耗出现较大偏差时，轮缘厚度的预警区间需要特定设置。

（3）不同里程下地铁车辆车轮轮缘厚度区间分布存在较大差异，预警区间随运行里程的增大而增大，应更早地跟踪和检测轮缘厚度，避免发生过度磨耗超限运行。