基于场路联合仿真BSG 的最大转矩电流比控制

李新华，徐竟成，余 朝

(湖北工业大学，武汉430068)

0 引 言

永磁同步电动机最大转矩电流比MTPA(Maximum torque per ampere)控制，是指通过合理分配交直轴电流以达到单位电枢电流所产生的电磁转矩最大的一种控制策略。在弱混合动力汽车起动时，皮带式起动-发电机BSG(Belt -driven starter generator)作为电动机提供大扭矩输出，使发动机起动至怠速。BSG 采用MTPA 控制，能够降低电机铜耗和逆变器损耗，节约电池电量。

在永磁同步电动机最大转矩电流比控制研究方面取得了较大进展。文献［1］提出一种在线搜索最大转矩角的控制策略;文献［2］在此基础上提出多项式拟合初始转矩角的变步长搜索法，但初始转矩角计算的误差及转矩角步长变化都会引起转矩振荡;文献［3］、［4］提出利用有功功率信号处理得到最大转矩角的控制方法，但这种方法不适用BSG 低压低频和大电流起动过程中的最大转矩角计算;文献［5］、［6］利用参数辨识进行交直轴电流最优分配的控制策略，但计算误差会造成最大转矩电流比控制最优点的偏移。

本文利用逆变器输出电压和电流中的谐波分量进行电机参数辨识，进而计算BSG 的最大转矩角，并通过补偿实现BSG MTPA 控制。为此，本文首先构建基于有限元仿真软件Maxwell 和电路仿真软件Simplorer 的BSG MTPA 控制联合仿真平台，其中BSG 模型由Maxwell 导出，在Simplorer 中搭建硬件电路及控制策略;在此平台上进行BSG 的参数辨识，并确定最大转矩角。BSG 现场电动实验结果表明，场路联合仿真与现场实验结果吻合良好。

1 BSG MTPA 控制系统

图1 为BSG 转子结构示意图。电机转子上有两个励磁源:一是励磁槽内放置的直流励磁绕组;另一个是励磁槽口嵌放的切向充磁永磁体和转子表面放置的径向充磁永磁体。BSG 具有十分优异的调磁特性，特别是解决了现有混合励磁BSG 过压保护难题。

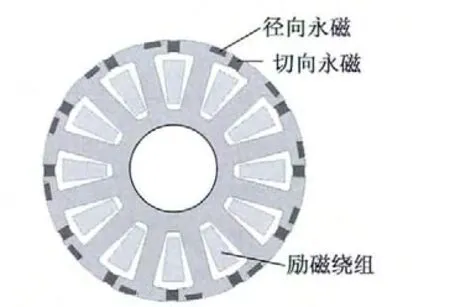
图1 BSG 转子结构示意图

BSG MTPA 控制系统框图如图2 所示。电机励磁电流由速度反馈调节，根据MTPA 算法确定d，q轴电流，经过电流内环和速度外环调节，最终达到BSG 最大转矩输出。

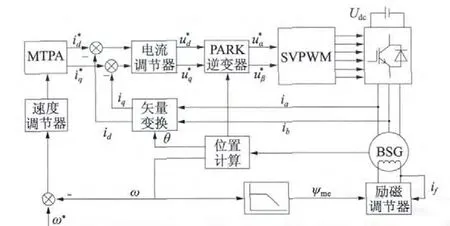
图2 BSG MTPA 控制系统结构框图

Park 坐标系下BSG 的转矩方程:

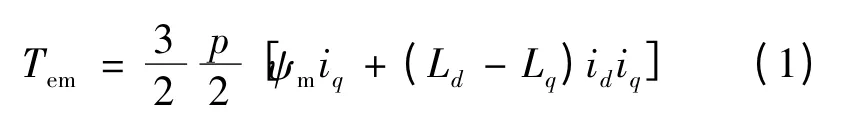
式中:p 为电机极数;id，iq分别为d，q 轴电流;Ld，Lq分别为d，q 轴电感;ψme为电机转子上的合成磁链，即:

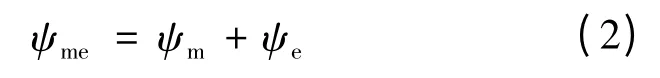
式中:ψm，ψe分别为BSG 的永磁磁链和电励磁磁链。

BSG 以最大转矩起动，合成磁链ψme应达到最大，且磁链值维持不变。

用转矩角β 表示的d，q 轴电流:

式中:is为定子电流。

BSG 采用MTPA 控制时电流矢量应满足:

联立以上式子可以得到BSG MTPA 控制下的最大转矩角:

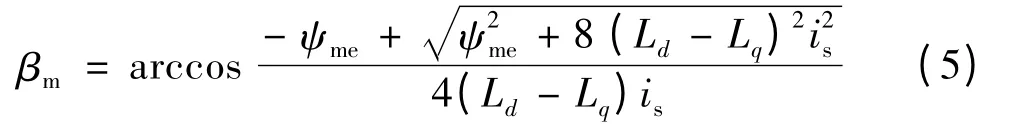
可见，最大转矩角βm与BSG 的d，q 轴电感Ld和Lq和合成磁链ψme有关。

2 βm 角的确定与补偿

参数的准确辨识是提高系统控制性能的前提，因此，最大转矩角βm的计算必须考虑电机磁路饱和对参数的影响。

考虑电机谐波后d-q 坐标系下的电压方程:

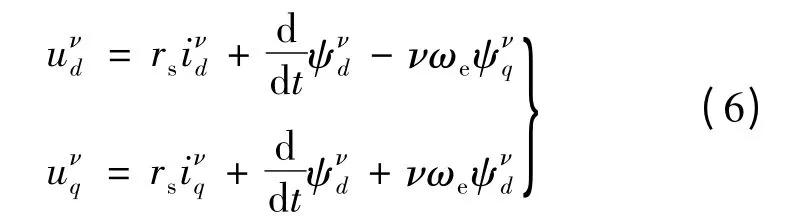
式中:ud，uq为d，q 轴电压;ψd，ψq为d，q 轴磁链;ωe为转子电角速度;ν 为谐波次数。

考虑谐波后的磁链方程:

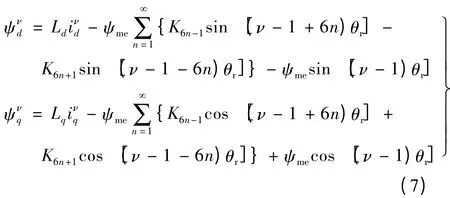
式中:θr为转子位置角;系数Kn(Kn≤1.0)的数值大小与反电动势幅值无关，只取决于反电动势的波形，定义K1=1.0［7］。

取电枢电流中的基波和7 次谐波用于参数计算，由式(6)可以得到电压方程组:

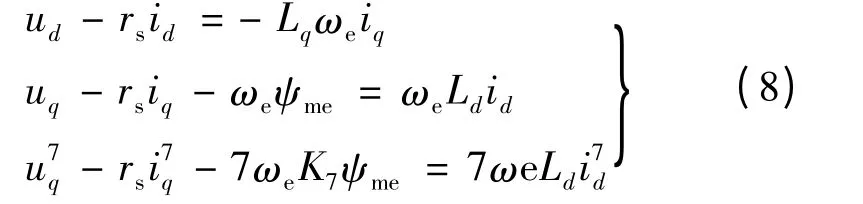
式中:rs为定子绕组电阻。d，q 轴电压和电流以及7次谐波d，q 轴电压和电流可以通过BAG 电机场路联合仿真求出;ωe由位置传感器测得。故由式(8)可以求出BSG 参数Ld，Lq和ψme。

根据参数辨识计算出的最大转矩角与实际情况存在一定的误差，使得BSG 并不是运行在MTPA 控制的最优点。因此需要以最大转矩角计算值β 为基准，补偿一定的角度Δβ，且满足以下关系式:

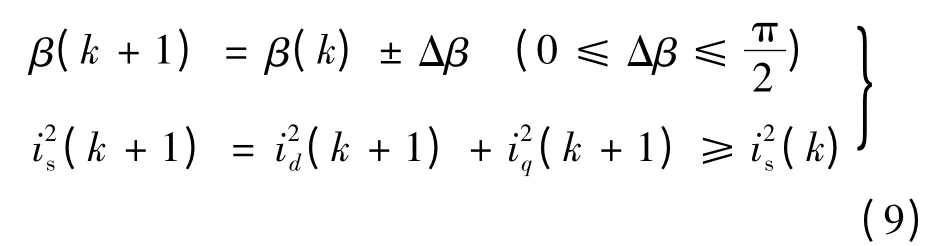
式中:β(k)，is(k)及β(k +1)，is(k +1)分别表示k与k+1 次补偿的转矩角和定子电流峰值。

BSG 电动过程中电磁转矩Tem一定，补偿后转矩电流比Tem/is大于补偿前即达到MTPA 控制，图3 为最大转矩角补偿算法流程图。

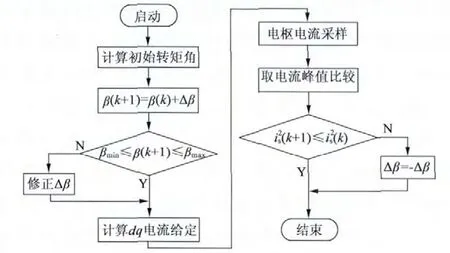
图3 转矩角补偿算法流程图

图4 给出了基于参数辨识BSG MTPA 控制算法原理框图。采样得到三相电压、电流及转子电角度后再经过坐标变换及低通滤波，得到基波和7 次谐波下d，q 轴等效电压和电流;然后通过参数辨识计算出d，q 轴等效电感及磁链，进而求得初始最大转矩角，同时在运行过程中加入转矩角补偿环节，最后进入MTPA 控制。

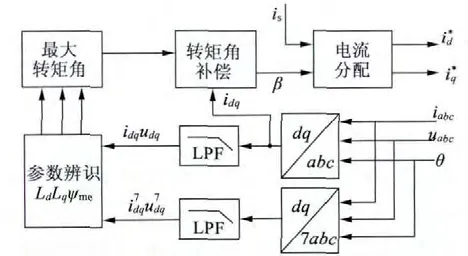
图4 参数辨识MTPA 原理框图

3 联合仿真及现场实验

基于Maxwell -Simplorer BSG MTPA 联合仿真模型如图5 所示。图中速度环、电流环、MTPA 模块和SVPWM 模块与MATLAB 仿真模型基本相同，需要调整的是与Maxwell 电机模型的对接部分;此外，考虑到BSG 低压大电流，定子三相绕组采用△接法。

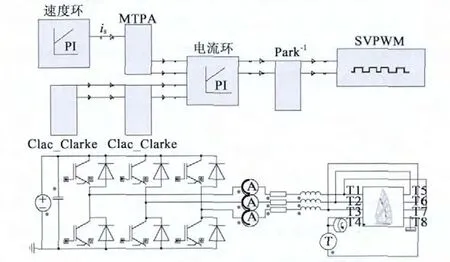
图5 基于Simplorer-Maxwell BSGMPTA 联合仿真模型

依次增加BSG 电动时的负载转矩，通过辨识计算得到电机参数随定子电流的变化关系;与此同时，对BSG 样机进行参数实验，通过电压电流积分法［8］计算d，q 轴电感。图6 给出了d，q 轴电感的仿真和现场实验结果。

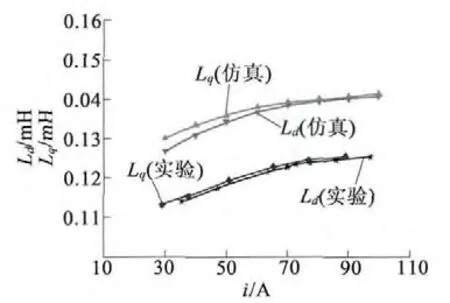
图6 d，q 轴电感随电流变化曲线

从图6 可以看出，在励磁电流一定的条件下，Ld略小于Lq，且随电流增加而增加，最后趋于饱和，显然，BSG d，q 轴电感的变化规律与普通内置式永磁同步电机并不相同;电感仿真数值接近实验数值，变化趋势与实验结果相符，验证了参数辨识结果的正确性。图7 是利用电机参数辨识结果得到MTPA 控制下d，q 轴电流的关系。

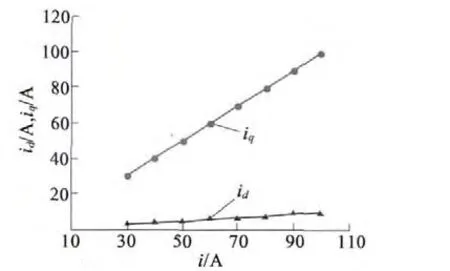
图7 d，q 轴电流随电枢电流变化曲线

对BSG 在MTPA 控制条件下进行联合仿真和现场电动实验。电机以50 r/min 转速带7 N·m 负载，图8、图9 分别是BSG 电机d，q 轴电流和电枢电流的仿真与实验波形。可见，场路联合仿真与电动实验波形基本吻合，即在BSG 电动过程中，按照MTPA 控制合理分配d，q 轴电流，以达到最大转矩输出下最小电枢电流的效果。

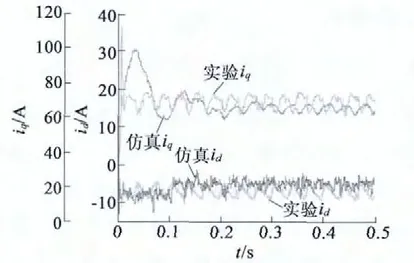
图8 电动过程d，q 轴电流

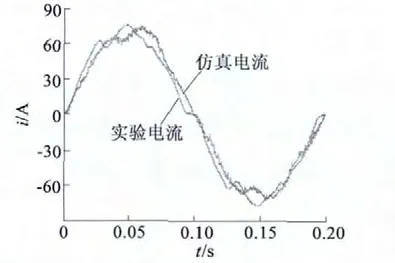
图9 电枢电流的仿真与实验波形

图10 是BSG 电枢电流的仿真和实验波形及其傅里叶分析结果。可以看出，逆变后电枢电流中7次谐波电流分量相对较大，可用于参数辨识计算。随着电机电枢电流的增大，定子磁链逐渐饱和，BSG的最大转矩电流比也随之改变。

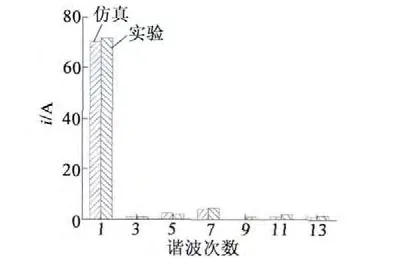
图10 电枢电流的傅里叶分析

图11 为在MTPA 条件下MATLAB 仿真、场路联合仿真、现场电动实验Id≠0 与Id=0 时的转矩电流关系曲线。与MATLAB 仿真相比，联合仿真中考虑了电机参数变化及磁路饱和情况，最大转矩输出随电流增大而趋于平缓，得到的仿真结果与现场电动实验Id≠0 结果比较吻合。

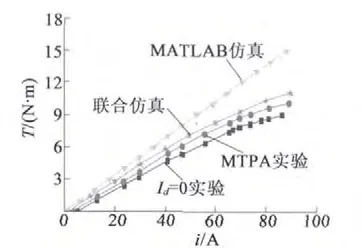
图11 不同控制策略的转矩特性

4 结 语

本文进行了基于参数辨识BSG 场路联合仿真的MTPA 控制研究。利用逆变器输出的谐波分量进行BSG 的参数辨识，加入转矩角补偿环节搜寻最大转矩角，从而达到MTPA 控制目的。联合仿真与现场实验结果验证了基于参数辨识BSG MTPA 控制的可行性和准确性。

［1］ ANTON D，KIM Y - K，LEE S - J，et al. Robust self - tuning MTPA algorithm for IPMSM drives［C］//34th Annual Conference of IEEE Industrial Electronics，Suwon，South Korea，2008:1355 -1360.

［2］ 廖勇，武泽东，刘刃. 车用永磁同步电机的改进MTPA 控制策略研究［J］.电机与控制学报，2012，16(1):12 -17.

［3］ BOLOGNANI S，PETRELLA R.Antomatic tracking of MTPA trajectory in IPM motor drives based on AC current trajectory［C］//IEEE Energy Conversion Congress ＆ Exhibition，2009，2:2350 -2346.

［4］ KIM S，YOON Y-D.Maximum torque per ampere (MTPA)control of an IPM machine based on signal injection considering inductance saturation［J］.IEEE Trans. on Power Electronics，2013，28(1):488 -497.

［5］ UNDERWOOD S J，HUSAIN I.Online parameter estimation and adaptive control of permanent -magnet synchronous machines［J］. IEEE Trans. on Industrial Electronics，2010，57(7):2435-2443.

［6］ KHANH N Q，PETRICH M，ROTH-STIELOW J.Implementation of the MTPA and MTPV control with online parameter identification for a high speed IPMSM used as traction drive［C］//The 2014 International Power Electronics Conference. IEEE，2014，318 -323.

［7］ NIAZI P，TOLIYAT H A. Online parameter estimation of permanent - magnet assisted synchronous reluctance motor［J］. IEEE Trans. on Industrial Applications，2007，43(2):609 -615.

［8］ SOONG W L.Inductance measurements for synchronous machines［R］.Power Engineering Briefing Note Series，2008:7 -8.