永磁同步电机损耗分离方法研究

于明湖，张玉秋，乔正忠，张 波，郑军洪

(1.华南理工大学，广州510641;2.美的集团，顺德528333)

0 引 言

搭载永磁同步电机的变频空调，以能效高和舒适度好等优点，逐渐成为行业的主流发展方向，从而对永磁同步电机的性能和可靠性提出了更高的要求。电机损耗不但浪费了能源，同时造成电机发热，降低了电机的可靠性。电机损耗主要包括铜耗、铁耗、附加损耗(杂散损耗)和机械风摩损耗。现有文献资料对各项损耗的机理、理论算法和基本实验方法进行了描述，很少有理论对比实验的详细结果［1-9］。

本文使用有限元软件，在空载、加载正弦电流和加载实测电流三种不同工况下仿真相关结果，同时优化设计损耗分离实验，分析比较仿真计算结果与实验结果，总结出仿真修正系数或实验测试的相关规律。

1 损耗的机理分析

电机损耗主要由铜耗pcu、铁耗pfe、杂散损耗ps和机械风摩损耗pfw组成。

1.1 铜耗

定子电流流经定子绕组，引起绕组产生的焦耳热，即为铜耗，计算公式:

式中:I 为相电流;R 为运行温度下的相电阻。

值得注意的是，在高频下，受“集肤效应”的影响，电阻R 增大，铜耗也会相应增大。一般来说，频率越高，绕组截面积越大，集肤效应越明显。

1.2 铁耗

目前，比较通用的铁耗计算是1988 年由Bertotti提出的三项式模型，表示如下:

式中:ph为磁滞损耗;pc为经典涡流损耗;pe为附加涡流损耗;Kh为磁滞损耗系数;Kc为涡流损耗系数;Ke为附加涡流损耗系数;f 为电频率;Bm为最大磁密。

系数Kh，Kc和Ke与铁磁材料相关，同一材料在不同频率下的铁耗系数也不相同。

1.3 杂散损耗

杂散损耗又称附加损耗，是由定子电流和转子永磁体产生的漏磁场及高次谐波磁场，以及由气隙磁场变化而引起的损耗。在稀土永磁同步电机中气隙磁密含有丰富的谐波分量，杂散损耗直接关系到电机效率的高低，而且气隙谐波磁场是产生杂散损耗的主要原因。

现有变频空调需要通过变频器向永磁电机供电，输入电流中包含由变频器斩波引入的高次谐波。

受电机结构本身与供电电源影响，在实验设备允许的情况下，杂散损耗应以实测值为准。

1.4 机械风摩损耗

电机运转时，由旋转轴与轴承相互摩擦、转子与空气摩擦以及联轴器摩擦等原因引起的损耗统称机械风摩损耗。机械风摩损耗主要和摩擦面承受的压力和摩擦系数有关，不同工装、不同的装配方式均会导致机械风摩损耗的不同。就旋转式永磁同步电机而言，机械风摩损耗的大小与转速n 成正比。

2 损耗的有限元计算

2.1 仿真机理分析

有限元软件一般采用加载电流源的方式进行负载计算，电磁转矩的计算不考虑电阻和铁耗的影响，即在设定的电磁转矩下，计算电流不受电阻和铁耗的影响。按Id=0 的控制方式，则相电流计算公式:

式中:Pe为电磁功率;P2为输出功率;m 为相数;E0为相反电势。

本文认为:

P1为输入功率，其依据在2.3 节中详细论述。

对于铁耗的计算，有限元软件通过硅钢材料的BP 曲线，拟合计算出铁耗系数Kh，Kc和Ke。其中，Kc的计算公式如下:

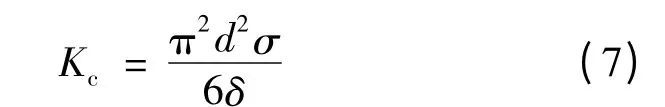
式中:d 为硅钢片厚度;σ 为电导率;δ 为硅钢片质量密度。

进一步，运用最小二乘法拟合可得出Kh和Ke。

2.2 空载仿真

实验电机的基本参数如表1 所示。其中，硅钢材料选用35CS300，永磁体选用42H。

表2 是在转速分别为1 200 r/min，1 800 r/min和3 600 r/min 下的空载铁耗。

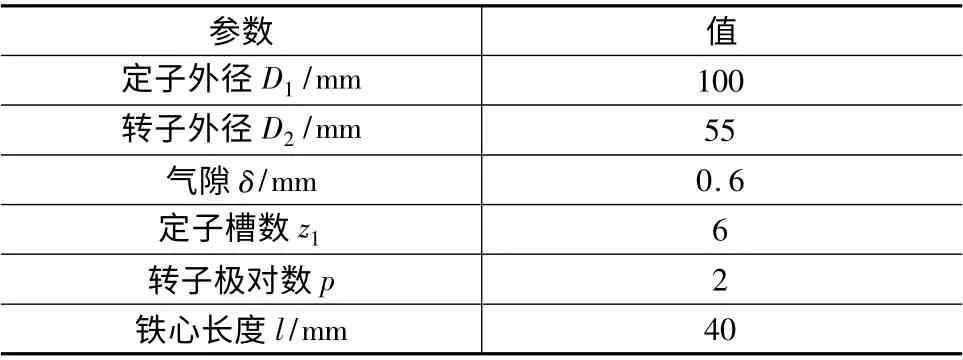
表1 实验电机基本参数

表2 空载铁耗仿真结果

2.3 加载正弦电流的负载仿真

设定电磁转矩2.5 N·m，分别仿真计算1 200 r/min、1 800 r/min 和3 600 r/min 下的负载铁耗。表3 是转速为1 200 r/min、1 800 r/min 和3 600 r/min 下的铁耗和电流计算结果。表4 是空载铁耗与负载铁耗结果对比。

表3 负载铁耗与电流仿真结果

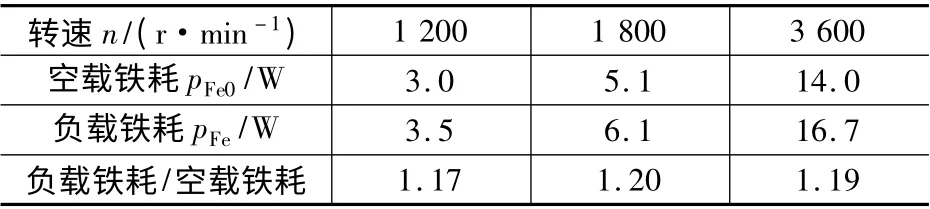
表4 空载铁耗和负载铁耗对比

从表4 数据可知，加载正弦电流的额定负载下，负载铁耗/空载铁耗约为1.2，空载铁耗与负载铁耗差异不大，即在定频条件下，铁耗受负载变化影响很小，因此在大多文献资料中铁耗被称为不变损耗。因此，工程上也常用空载铁耗(基本铁耗)等效负载铁耗。

上述结果与永磁同步电机的运行特点相符合，即永磁同步电机由装配有永磁体的转子提供主磁通。电机运行时，定子铁耗主要是由转子旋转而导致主磁通变化引起的，而电磁功率驱动转子旋转。根据能量守恒定律和功率流规律，可知电磁功率中包含了基本铁耗，即Pe=P2+pfe+pfw=P1-pcu。

2.4 加载实测电流的负载仿真

在额定转速3 600 r/min，额定输出转矩2.5 N·m下，记录采样率为500 kHz 的实测电流波形，实测电流波形如图1 所示。

图1 实测电流波形

设 置 步 长 为 0. 000 02 s，0. 000 01 s，0.000 005 s 和0.000 002 5 s 分别进行仿真，表5 是不同步长下的铁耗计算结果。

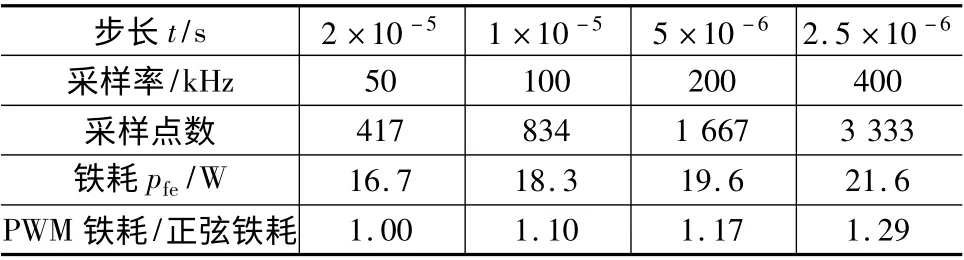
表5 不同步长下的铁耗仿真结果

从表5 数据可知，随着步长的减小，采样率和采样点数在增加，波形越趋于实测值，高次谐波的影响加大，铁耗呈上升趋势。在采样率400 kHz 下，其与正弦电流下铁耗计算值的比例系数约为1.3，与电机及控制联仿结果接近，从而具有一定的准确性。

3 实验设计与优化验证

采用主动式测功机测试系统进行空载试验和负载试验，依据能量守恒定律对电机损耗进行逐项分离。实验用测功机采用同轴双机系统，测试系统示意图如图2 所示。待测电机与伺服马达同轴相联，中间通过联轴器安装有扭力检出计。伺服马达既可作为原动机拖动待测电机，也可作为负载运行。

3.1 空载试验

试验方法:

(1)伺服电动机拖动不带磁转子，测得的输出功率即为机械风摩损耗pfw;

(2)伺服电动机拖动待测电机，测得的输出功率为空载总损耗p0，可得空载铁耗:

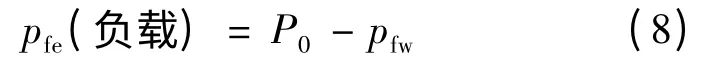
因测试台位误差，按常规测试方法测出的机械风摩损耗包含有零漂的非真实值，且波动较大;测出的空载铁耗波动也较大。可利用以下方法对试验及数据处理做优化调整，提高测试准确度。

(1)伺服电动机拖动不带磁转子，在CCW 转向和CW 转向下分别测得pfw1和pfw2，设定p01为无磁零漂，可得:

由式(9)可计算出实际机械风摩损耗pfw和无磁零漂p01。

(2)同(1)可测出实际空载总损耗p0和带磁零漂p02。由优化后的实际机械风摩损耗和实际空载总损耗按式(8)优化计算空载铁耗。

表6 是不同实验台位优化前和优化后两种方法得出的机械风摩损耗和空载铁耗对比。

表6 中，Δ 表示最大偏差率。从表中数据可知，机械风摩损耗按优化前和优化后的方法测试分析出的结果相差很大，这是因为调整前测出机械风摩损耗中包含了空载零漂，同时，优化后测得的机械风摩损耗较优化前波动小、一致性好;优化后测得的空载铁耗较优化前波动性小、一致性好。

表6 优化前后机械风摩损耗与空载铁耗对比

3.2 负载试验

试验方法:

变频器驱动待测电机通过联轴器连接测功机运转，测得输入功率P1、输出功率P2、定子相电流I、定子相电阻R(运行时的瞬态电阻)，根据焦耳定律和电机运行功率流，负载下各项损耗可通过下式进行分离:

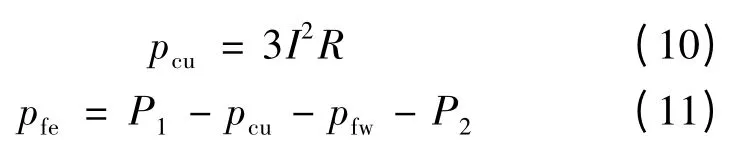
负载下，测功机同样存在负载零漂，测得的输出转矩并非真实值，即测得的输出功率并非真实值。在不同零漂下，测得的总损耗与电机效率并非真实值且存在较大的波动。本文提出一种修正方法，可将不同基准下的总损耗修正到同一水平，进而可对电机效率进行修正。

试验方法优化:

不同基准测试前，采用修正杠杆和砝码，记录实际砝码扭力T2和对应测试扭力T＇2，由此修正负载下的总损耗:

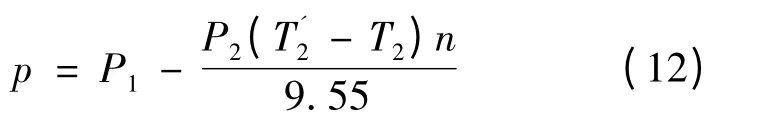
表7 是定转矩2 N·m、不同基准下优化前与优化后两种方法测得的总损耗对比。

从表7 数据可知，优化前方法测得的总损耗波动很大，试验与分析方法优化后，可将总损耗修正到基本相当，从而可进一步将电机效率修正到基本相当的结果。

图2 测试系统示意图

表7 优化前后总损耗对比

3.3 杂散损耗试验研究

在变频器供电时，电机输入电流引入由斩波引起的高次谐波。一般情况下，测试时采用低通滤波来消除高次谐波的影响。当滤波频率大于变频器斩波频率或无滤波时，需要考虑高次谐波附加的损耗。

高次谐波的附加损耗是杂散损耗的主要部分。本文设计实验方法测试和分析杂散损耗。

由上述可知，空载铁耗(基本铁耗)接近于负载铁耗，可将负载附加损耗ps分离出来:

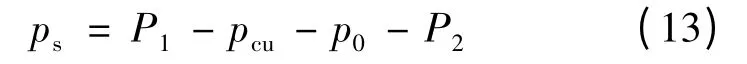
负载附加损耗是在测试电机输入负载电流之后，由电流基波、绕组谐波、变频器谐波等引起的附加损耗，主要成分是附加铁耗。因电流基波下的铁耗与基本铁耗比较接近，可认为负载附加损耗的主要成分是电流谐波引起的铁耗，这与杂散损耗的成分是基本相同的。因此，杂散损耗可近似用式(13)进行分离。

4 仿真与试验结果对比

电机的各项损耗中，铁耗、铜耗和杂散损耗通过有限元仿真计算与试验分离均可分析出结果，机械风摩损耗仅与测试台位和装配条件等相关，仅能通过试验所得。因此对铁耗、铜耗和杂散损耗的仿真结果与试验结果进行分析对比。

4.1 铁耗

基本铁耗仿真结果与实测结果如表8 所示。从表8 数据可知，空载铁耗修正系数(实测/仿真)在不同频率下基本相当，约为1.1，即实测结果与仿真结果接近，同时验证了结果的准确性。

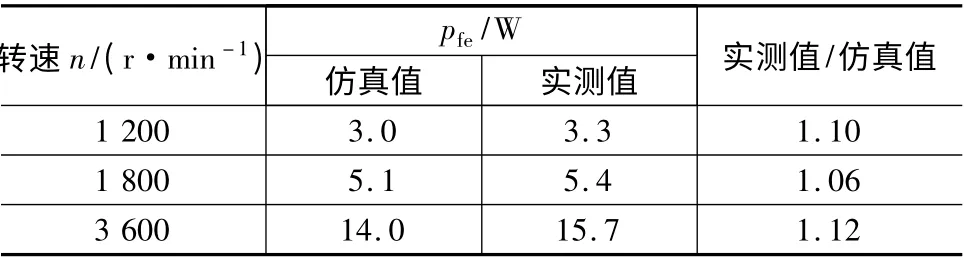
表8 基本铁耗仿真与试验结果对比

4.2 铜耗

仿真计算和试验测试铜耗，都是先得到电流I，根据实际电阻按公式(10)计算铜耗。由此，本文仅对比仿真与实测的电流结果。表9 是实验电机在额定输出转矩2.5 N·m 下，转速分别为1 200 r/min、1 800 r/min 和3 600 r/min 的仿真与实测电流对比。

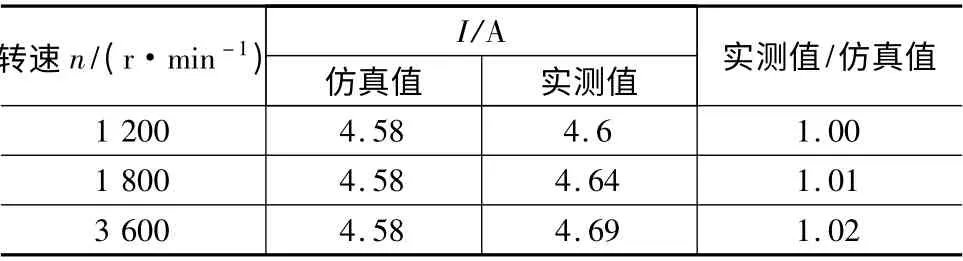
表9 电流仿真与实测结果对比

从表9 数据可知，不同频率的电流修正系数(实测/仿真)基本为1，即仿真电流与实测电流基本相同，从而验证了仿真结果的准确性。

4.3 杂散损耗

考虑加载实测电流波形的有限元仿真计算量大、计算时间长，现只在转速3 600 r/min、转矩2.5 N·m 下加载实测电流波形进行仿真计算，同时采用波动性较小的测功机进行负载试验，并进行结果分析处理。表10 是杂散损耗仿真结果与实测结果对比。

表10 杂散损耗仿真与实测结果对比

从表10 可知，PWM 谐波影响下的铁耗和杂散损耗的实测值与仿真值接近，验证了结果的准确性。

4.4 电机性能验证

将有限元计算的各项损耗经过前文得出的修正系数(空载铁耗修正系数取1.1，铜耗修正系数取1.0，杂散损耗/正弦负载铁耗系数取0.3)进行修正(机械风摩损耗暂用实测值)，定扭力2.5 N·m 下运用损耗的仿真修正结果，计算电机的效率并与实测电机效率进行对比，对比结果如表11 所示。

表11 电机效率计算与实测结果对比

从表11 可知，采用仿真结果及修正系数计算的电机效率与实测电机效率基本相同，进一步验证了本文所述方法的准确性，可有效地指导永磁电机设计。

5 结 语

基于有限元分别对永磁同步电机进行空载仿真、加载正弦电流和加载实测电流的负载仿真，计算出基本铁耗、铜耗和不同电流的负载铁耗，设计并优化损耗测试实验，对损耗进行逐项剥离，对比仿真计算结果和实测结果，总结出修正系数或相关规律，经过验证，性能计算结果与实测结果一致性好，可有效指导永磁电机的性能设计。

［1］ 唐任远.现代永磁电机理论与设计［M］. 北京:机械工业出版社，1997.

［2］ 王鹏，陈阳生，陈致初. 永磁同步电机不同工况下定转子铁耗分析［J］.机车电传动，2012，(1):11 -15.

［3］ 顾德军，陈伟华，张维，等.超高效电机杂散损耗参数带的选取［J］.电机与控制应用，2011，38(7):48 -52.

［4］ 周云山，张立辉. 电机定子铁损试验的研究［J］. 东方电机，2009，(1):30 -33.

［5］ Katsumi Yamazaki.Torque and efficiency calculation of an interior permanent magnet cotor considering harmonic iron losses of both the stator and rotor［J］.IEEE Transactions on Magnetics，2003，39(3):1460 -1463.

［6］ BOGLIETTI A，FERRARIS P，LAZZARI M，et al.About the possibility of defining a standard method for iron loss measurement in soft magnetic materials with inverter supply［J］.IEEE Transactions on Industry Applications，1997，33(5):1283 -1288.

［7］ ATALLAH K，ZHU Z Q，HOWE D.An improved method for predicting iron losses in brushless permanent magnet DC drives［J］.IEEE Transactions on Magnetics，1992，28(5):2997 -2999.

［8］ ZHU Z Q.Iron loss in permanent-magnet brushless AC machines under maximum torque per ampere and flux weakening control［J］.IEEE Transactions on Magnetics，2002，38(5):3285 -3287.

［9］ WANG Jiabin，IBRAHIM T，HOWE D. Prediction and measurement of iron loss in a short-stroke，single-phase，tubular permanent magnet machine［ J］.IEEE Transactions on Magnetics，2010，46(6):1315 -1318.