基于非线性主成分分析的综合国力评价模型研究

程 毛 林

(苏州科技学院 数理学院，江苏 苏州 215009)



基于非线性主成分分析的综合国力评价模型研究

程 毛 林

(苏州科技学院 数理学院，江苏 苏州 215009)

摘要：如何构建一种定量的综合国力评价模型具有重要意义。当前评价综合国力的方法不多，一般方法易受主观因素影响。本文给出非线性主成分分析综合评价方法，有较好的稳定性和可靠性。利用该方法，本文对世界主要国家的综合实力进行了评价。

关键词：综合国力；非线性；主成分分析；评价模型

近几年，不少学者对综合国力评价进行了很多的研究[1-6]，但一般研究是利用指数加权法、功效系数法、模糊综合评价法等。多元统计分析方法较难使用，主要原因是研究对象一般是一些主要国家，样本点较少，而评价指标较多，为此本文使用分层主成分分析方法，对每小层分别利用主成分分析(指标少)，再对这些小层的总得分进行主成分分析。另一方面，线性主成分分析法的综合评价，是对各主成分用各自贡献率加权，其结果主要取决于第一主成分贡献率(最大)。为了提高第一主成分贡献率，本文给出广义Box-Cox变换，使得变换后得到的非线性主成分第一主成分贡献率有最大值。

1综合国力评价指标体系

本文参考多家研究机构的研究成果[7-10], 选取下列综合国力评价指标：

(1) 领土与自然资源。其构成：领土总面积，石油探明储量，天然气探明储量。

(2) 人口因素。其构成：老龄化程度，高等教育入学率，教育投入。

(3) 经济发展水平。其构成：GDP数值，人均GDP数值，竞争力指数。

(4) 军事能力。其构成：军费，军队人数，武器装备指数。

(5) 科技水平。其构成：研发投入占GDP比重，每百万人从事研发的人数，诺贝尔获奖人数。

(6) 社会发展。其构成：人类发展指数，基尼指数。

(7) 安全与国内政治。其构成：和平指数，清廉指数。

(8) 国际贡献。其构成：联合国会费，联合国维和费用，参与维和人数。

2非线性主成分分析综合评价模型

传统的主成分分析方法[11-13]在一些情况下降维作用不好，而且一般只能处理线性问题。因此本文提出了一种基于非线性主成分分析的综合国力综合评价方法，该方法通过广义Box-Cox变换，选择广义Box-Cox变换参数，使得变换后的新数据进行主成分分析第一主成分贡献率取最大值,这种非线性变换使降维作用显著。

2.1广义Box-Cox 变换

Box-Cox变换是常用的数据变换方法，本文给出广义Box-Cox变换，即

其中，λ1,λ2为两个待确定的参数，要求X+λ2>0,这个变换实际上是对X作平移后再作Box-Cox变换，一般的Box-Cox变换含一个参数，此广义Box-Cox变换是一般Box-Cox变换的推广。对X为非负数值的情况下可使用此广义Box-Cox变换。若有负值，可有下式变换

其中，sign为符号函数，λ1,λ2为两个待定参数。

2.2非线性主成分分析综合评价步骤

步骤1：给定广义Box-Cox变换中λ1,λ2的变化范围，选择λ1,λ2的值，从小到大依次选取(本文步长选择均为0.1)，并计算Box-Cox变换值，得到新的观测矩阵Y。

步骤2： 记矩阵Y为

再将Y数据进行标准化处理

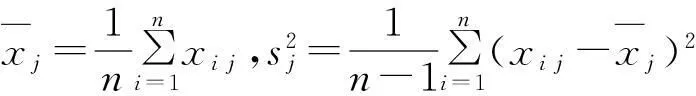
步骤3：对应于R，求特征方程|R-θI|=0的m个特征值θ1>θ2>…>θm≥0，特征值θi的特征向量为：

并且满足

于是得到m个主成分

……

第i个因子(主成分)的方差贡献率为

在综合评价中，第一主成分往往取决定性作用。

步骤4：对所有选择的每一对λ1,λ2按照步骤1-步骤3计算得到各自的第1个主成分方差贡献率，取最大的第一个主成分方差贡献率对应的λ1,λ2为广义Box-Cox变换的两个参数。

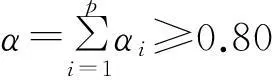
F=α1z1+α2z2+…+αpzp

计算得分大小，根据得分大小排序。

3综合国力评价应用

依据《世界统计年鉴2010》、中国社会科学院《2010年：全球政治与安全报告》等资料，选取西方7国，即美国、日本、法国、德国、英国、加拿大、意大利和金砖4国(即中国、俄罗斯、印度、巴西)等11国的资料分析评价。由于二级指标有22个，样本点只有11个，不可直接用主成分分析。这里使用分层主成分分析，保证每层主成分分析的样本点比指标数大。

本文对一级指标下的综合国力8个方面分别使用本文给出的主成分分析法， 8个方面分别用广义Box-Cox变换

参数取值结果见表1，广义Box-Cox 变换后的8个一级指标的主成分综合得分见表2。

对领土与自然资源、人口因素、经济发展水平、军事能力、科技水平、社会发展、安全与国内政治、国际贡献8个方面的主成分综合得分看作8个新变量再使用本文给出的方法，由于分值有负数，用广义Box-Cox 变换:

可得参数值λ1=0.1,λ2=2.1。变换后的第一主成分贡献率为78.743 5，原第一主成分贡献率为56.256 5。变换后使用主成分分析，得到综合国力总得分，见表2。

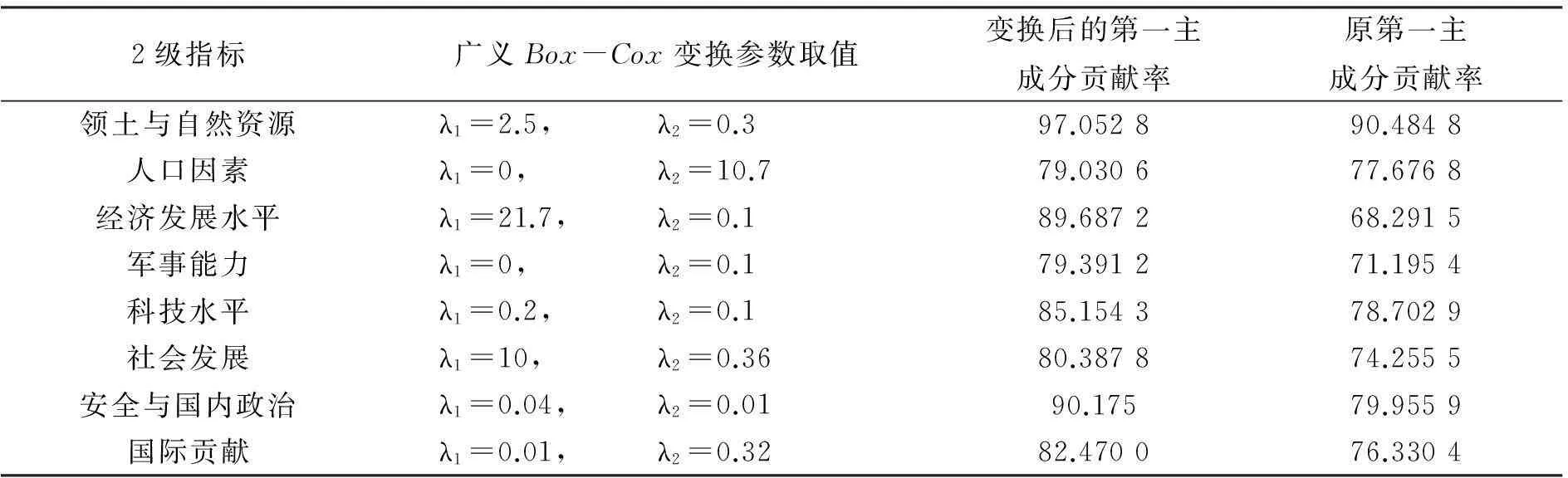
表1　 广义Box-Cox 变换参数结果

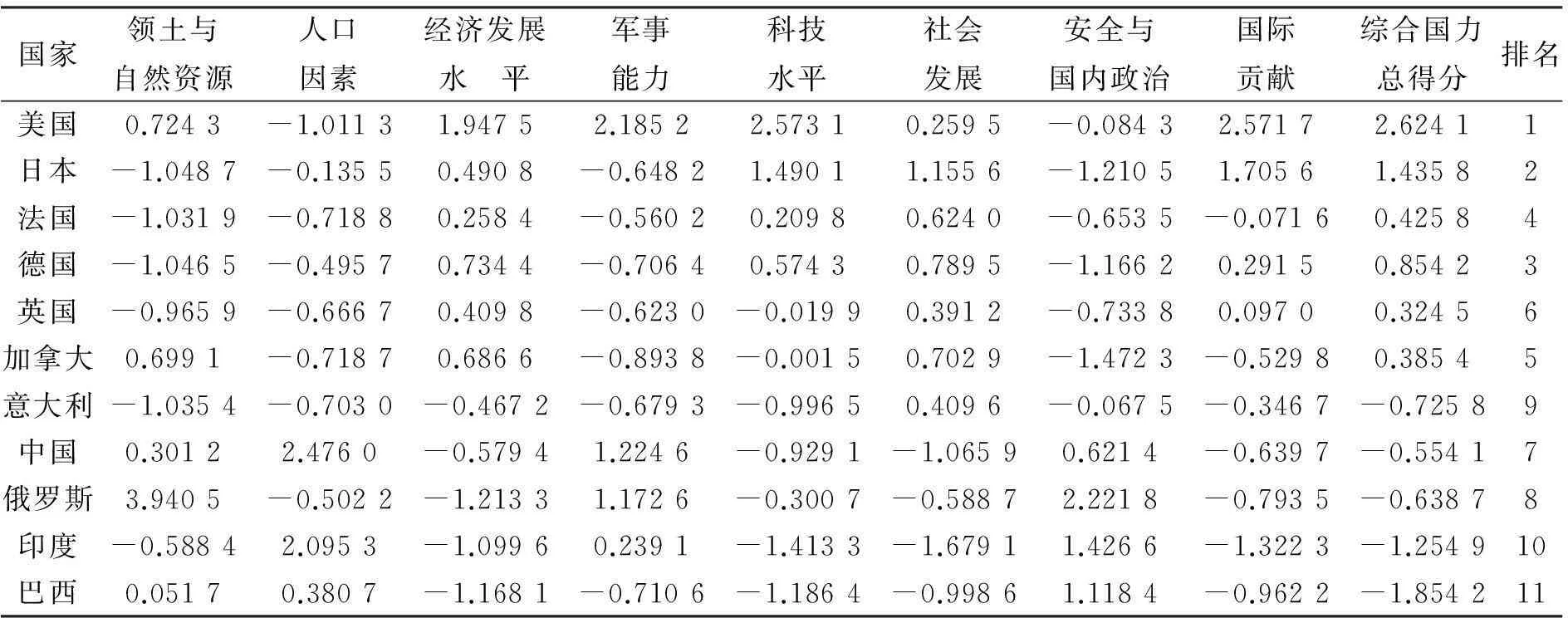
表2　八个一级指标的主成分综合得分及综合国力总得分

这里给出2010年中国社会科学院国际战略研究专家李慎明和王逸舟[14]用综合指数法计算的总得分及排序结果，见表3。

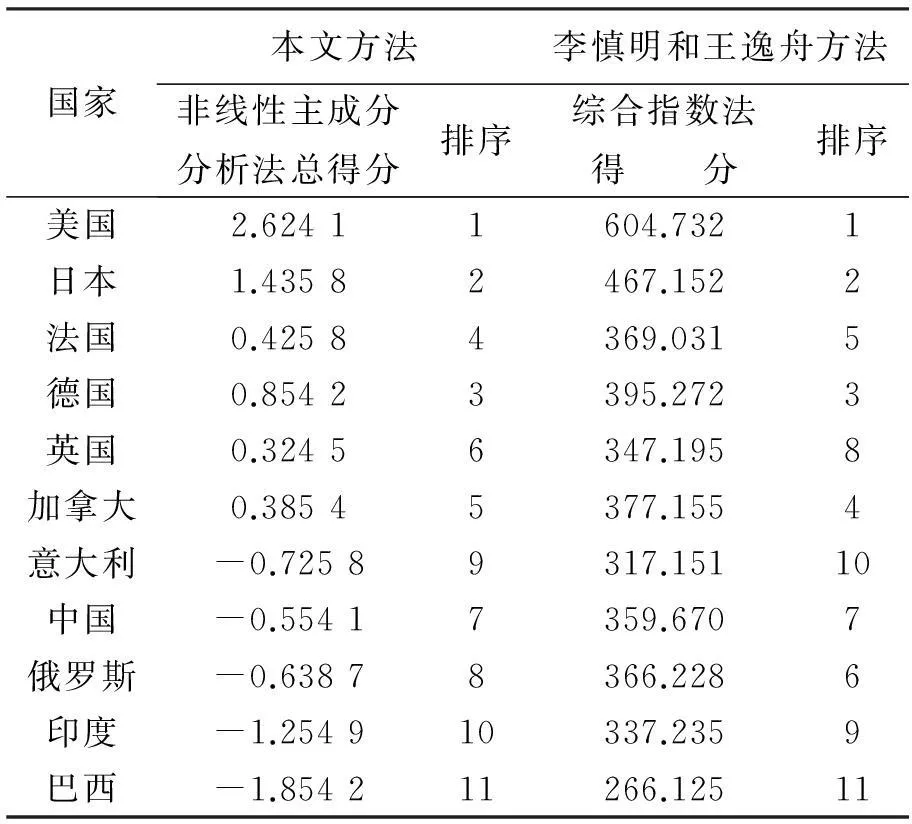
表3　两种方法计算结果比较

为比较表3中两种方法排序一致性的程度，计算斯皮尔曼等级相关系数

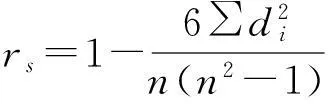
其中，di为第i个国家两种方法排序的差，n为样本个数11。从斯皮尔曼等级相关系数可见两种方法排序基本一致。

4结语

在综合国力评价上，一般方法易受主观因素影响，本文给出主成分分析法比较客观，评价函数其权数利用各主成分贡献率，且本文提出的一种基于广义Box-Cox变换的非线性主成分分析综合国力评价方法，使得主成分分析降维作用明显，这样分析的结果就比较稳定可靠。与李慎明和王逸舟的综合指数法比较，本文方法客观具体、科学可靠，而李慎明和王逸舟的综合指数法易受主观权数影响，且不同指标之间的可比性差。本文方法不足之处是Box-Cox变换中的两个参数取值不易掌握，计算稍复杂。

参考文献:

[1] 黄硕风. 大国较量(世界主要国家综合实力国际比较)[M].北京：世界知识出版社, 2006: 123-134.

[2] 晏雁. 中美两国综合国力定量化比较[J]. 中南财经大学学报, 2001(6): 38-43.

[3] 翟立功. 中国与西方七国综合国力最新比较[J]. 统计研究, 2000(5): 3-8.

[4] 施祖辉. 国外综合国力论研究[J]. 外国经济与管理, 2000, 22(1): 13-19.

[5] 孙亦舟, 邓淑华. 综合国力估量的前缘分析方法[J]. 数学的实践与认识, 2009, 39(6): 18-22.

[6] 王树禾. 综合国力的数学模型[J]. 高校应用数学学报, 1997, 12(1):29-36.

[7] 张莉. 综合国力评价初探[J]. 统计与决策, 2002(5): 9-10.

[8] 雷瑛.试论综合国力统计指标体系的建立[J]. 技术经济, 2000(6): 51-53.

[9] 王玲. 关于综合国力的测度[J]. 世界经济与政治, 2006(6): 45-51.

[10] 韩瑞玲, 路紫. 中国综合国力的增长及其国际比较[J]. 山东师范大学学报(自然科学版), 2008, 23(2): 77-80.

[11] 潘春光, 陈英武, 汪浩. 主成分分析法在基于度量的软件风险评估中的应用[J]. 运筹与管理, 2005, 14(5): 80-84.

[12] 郭馨梅. 基于主成分分析法的北京流通业资源利用效率综合评价[J]. 北京工商大学学报, 2012, 27(6): 19-24.

[13] 曾珍香, 段丹华, 张培, 等. 基于主成分分析法的京津冀区域协调发展综合评价[J]. 科技进步与对策, 2008, 25(9): 44-49.

[14] 李慎明, 王逸舟. 全球政治与安全报告(2010)[M]. 社会科学文献出版社, 2010: 257-276.

Research on Evaluation Model of Comprehensive National Power Based on Nonlinear Principal Component Analysis

CHENG Mao-lin

(School of Mathematics and Physics, Suzhou University of Science and Technology, Suzhou 215009, China)

Abstract:It is of great significance on how to construct a quantitative evaluation model of comprehensive national power. At present, there are a few methods for evaluating the comprehensive national power; and the general methods are subject to the subjective factors. In this paper, the comprehensive evaluation methods based on nonlinear principal component analysis is proposed and characterized by better stability and reliability. By virtue of this method, the comprehensive national power of major countries in the world is evaluated in this paper.

Key words:comprehensive national power, nonlinear, principal component analysis, evaluation model

文章编号：1007-4260(2015)03-0031-04

中图分类号：O212

文献标识码：A

DOI：10.13757/j.cnki.cn34-1150/n.2015.03.009

作者简介：程毛林，男，安徽桐城人，硕士，苏州科技学院数理学院副教授，硕士生导师，研究方向为应用统计、预测评价。

基金项目：全国统计科研计划项目(2013LY133)和江苏省自然科学基金(BK2012165)。

收稿日期：2014-10-14

网络出版时间：2015-8-25 15:40网络出版地址：http://www.cnki.net/kcms/detail/34.1150.N.20150825.1540.009.html