模糊可靠性分析中关于专家给出意见的整合

张　鑫，汤胜道

(安徽工业大学 数理科学与工程学院，安徽 马鞍山 243002)



模糊可靠性分析中关于专家给出意见的整合

张鑫，汤胜道

(安徽工业大学 数理科学与工程学院，安徽 马鞍山 243002)

摘要：在现实系统中，由于种种原因，某些部件的失效概率往往难以获得，通常采用模糊专家评估系统的方法去解决。如何将不同的专家意见整合成一条意见是一个关键问题，本文给出了一种新方法去整合专家意见，并用一个数值例子演示了所给的方法。

关键词：系统可靠性；专家意见；模糊概率；重合度

在系统可靠性指标评估分析的过程中，得到基本事件发生的概率是最重要的，但实际中很难得到其准确值，所以一般采用专家意见给出的方法来得到事件发生的模糊概率。在以往的文献中，大都是根据专家们的职称、工龄、受教育程度进行分层次选择并以此打分评出各个专家的权重因子，在各个专家给出意见后，将其意见通过隶属函数转换为模糊数组，最后将各专家的模糊数组结合其权重因子得到事件发生的模糊概率[1]。但是专家们由于种种原因不可能对某一事件有着完全不同的意见，V.R. Renjith等[2]不仅对专家进行了等级评估，还将专家们给出意见时的语气肯定程度纳入评判，形成二元模糊数组。Wang Daqing等[3]提出相似度概念，以各意见对应的模糊数组之间的重合部分的面积比作为该专家的权重因子，最后得到事件发生的模糊概率。本文在专家评估系统的基础上借鉴了相似度概念，将专家意见以重合次数进行分类并赋于权重，最后得到事件发生的模糊概率。

1模糊专家评估系统

由于系统中许多事件的发生无法获得确切地概率，所以采取专家意见给出的方式得到其模糊概率。先定义‘很低(VL)’、‘低(L)’、‘中等(M)’、‘高(H)’、‘很高(VH)’五个语义，对应的模糊数组分别记为A1，A2，A3，A4，A5，专家们从中选取自己所要给出的意见。专家意见所对应的尺度函数如图1所示。

图1

图1中的横轴表示专家语义的模糊数值，纵轴表示语义的隶属函数。若专家说：“很低”，则其表示事件发生的概率在区间[0，0.2]上取值，隶属函数说明[0，0.2]上不同取值的“很低”程度。各语义所对应的隶属函数如下

(1)

(2)

其中di指第i位专家的总得分。

表1　专家权重得分的打分项及分值

再根据Clemen和Winkler[4]提出的线性组合公式将专家给出意见转化为梯形模糊数

(3)

其中Bi表示第i位专家对事件发生概率的评估意见所对应的模糊数。

此模糊概率是从专家本身出发得到的权重因子将所有的专家意见整合后得到的。下面从专家意见的角度根据其重合次数将意见整合，得到事件发生的模糊概率M″。

以两个专家给出意见为例，如图2所示。两个专家对某事件发生的概率进行评估时，其所给意见可分为两部分：与他人意见相重合部分(记为2)，未与他人意见相重合部分(记为1)。即图2中S1的重合次数为1，S2的重合次数为2。

图2　两位专家选取意见的重合次数划分

当选取n位专家并得到其意见后，用上述方式将他们的意见进行划分。语义A1，A2，A3，A4，A5的选取人数分别为m1，m2,m3,m4,m5,如图3。

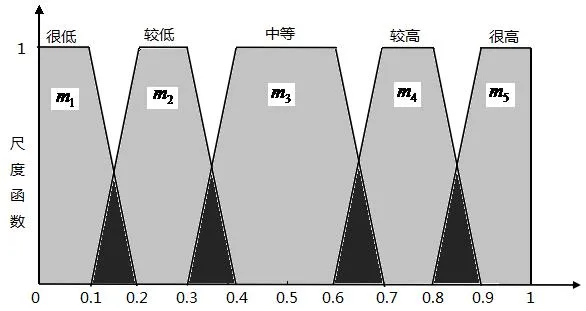
图3各模糊语义的专家选取人数

A1，A5被分成两个部分，A2,A3,A4被分成三个部分。A1的主体部分有m1位专家选取，其余部分被m2位专家选取；A2的主体部分有m2位专家选取，另外两部分分别有m1和m3位专家选取；A3,A4,A5同样如此划分。对专家来说，意见的主体部分最为重要，故在此认为意见体部分的重要性为其它部分的两倍。五个意见的重合度计算如下

(4)

第j(j=1,2,3,4,5)个意见的权重因子为

(5)

(6)

若M′=(a′,b′,c′,d′)，M″=(a″,b″,c″,d″)，则通过松驰因子α将模糊数M′和M″结合得

M=αM′+(1-α)M″=(a,b,c,d)

(7)

其中松驰因子0≤α≤1，其取值视具体情况需要而定。a,b,c,d取值如下

a=α·a′+(1-α)a″,b=α·b′+(1-α)b″

c=α·c′+(1-α)c″,d=α·d′+(1-α)d″

(8)

对应的隶属函数

(9)

再以下面公式将隶属函数转化为模糊概率

(10)

最后，事件发生的概率由Onisawa[5]所提出的公式进行转化

(11)

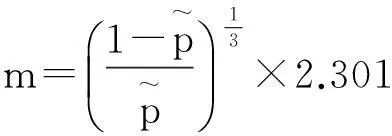
至此，我们求得事件的发生概率，解决可靠性分析中最重要最基本的部分，便可对系统进行定性定量地分析评估。

2数值例子

在分析太阳能发电系统的可靠性时需要知道太阳能电池的失效率，然而因为其型号多样且使用数量相对较少，故而很难通过数理统计手段得到准确值，所以采用模糊专家系统评估是一种很有效的方法。选取20位对太阳能电池十分了解的专家进行意见给出，并根据前文方法进行打分，如表2所示。

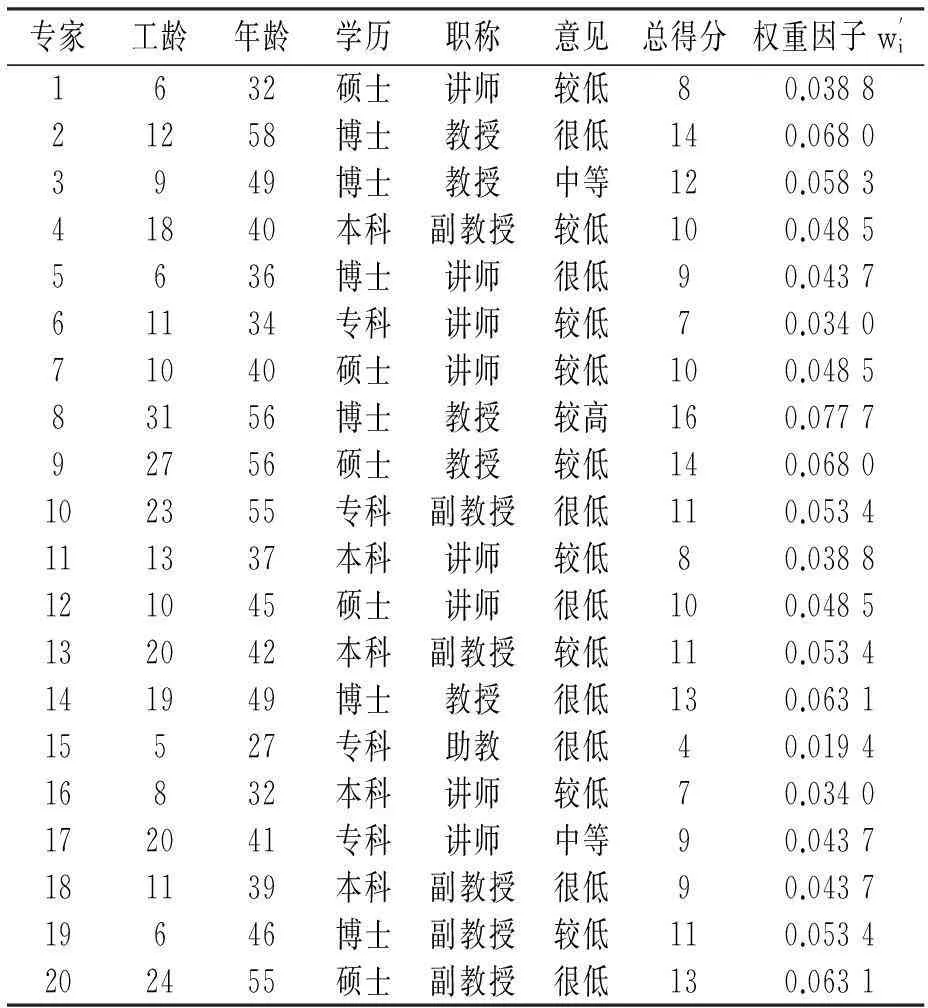
表2　 选取专家的权重因子及意见

根据公式(1)和(3)，得到太阳能电池失效率的梯形模糊数

(0.118 9,0.178 6,0.288 8,0.388 8)

此时根据公式(10)和(11)得到的概率为

p1=0.120 384

由表2知五个意见的选取人数分别为8,9,2,1,0，其对应的重合度由公式(4)可得

由公式(5)计算出各意见的权重因子为

w″1=0.344 8,w″2=0.289 7,w″3=0.186 2,

w″4=0.165 5,w″5=0.013 8

由公式(6)计算出梯形模糊数

(0.196 1,0.262 5,0.382 0,0.481 5)

(0.157 5,0.220 6,0.335 4,0.435 2)

对M作适当地放缩，得

M=(0.16,0.22,0.34,0.44)

根据公式(9)得到对应的隶属函数

由公式(10)得

最后由公式(11)得

p2=0.192 653 7

将p1和p2对比可发现两概率相差较大，说明单从专家本身得到权重因子来整合意见可能与多数人的意见不一致，所以应该将意见也纳入考察范围，使用松驰因子将二者结合更为合理。

3结束语

使用模糊专家意见评估系统给出事件发生的模糊语义，在解决系统中某些事件的发生概率难以得到时是十分有效的手段。本文以意见重合度来整合专家给出的意见，不仅仅考虑专家自身因素还将意见本身按照其认同多寡进行划分后再整合，这样可修正出现个别专家的权重因子过高而其意见选取人数很少的情况，从而保证采纳大多数专家的意见。

参考文献:

[1] Y.H.Dong, D.T.Yu. Estimation of failure probability of oil and gas transmission pipelines by fuzzy fault tree analysis[J]. Journal of Loss Prevention in the Process Industries, 2005,18(2): 83-88.

[2] V.R.Renjith, G.Madhu, A.B.Bhasi, et al. Two-dimensional fuzzy fault tree analysis for chlorine release from a chlor-alkali industry using expert elicitation[J]. Hazardous Materials, 2010, 183: 103-110.

[3] Daqing Wang, Peng Zhang, Liqiong Chen. Fuzzy fault tree analysis for fire and explosion of crude oil tanks[J]. Journal of Loss Prevention in the Process Industries, 2013, 26: 390-398.

[4] Clemen, Winkler. Combining probability distribution from experts in risk analysis[J]. Risk Anal, 1999, 19(2): 187-203.

[5] T.Onisawa. An approach to human reliability in man-machine systems using error possibility[J]. Fuzzy Sets Sys.,1998(27): 87-103.

Integration for Experts′ Opinions Based on Fuzzy Reliability Analysis

ZHANG Xin，TANG Sheng-dao

(School of Mathematics and Physics, Anhui University of Technology, Maanshan 243002, China)

Abstract:In real systems, it is often difficult to get failure probabilities of some components, for all kinds of factors. In this case, usually, fuzzy expert estimation is used to solve the problem. It is a key access how to aggregate different experts′ opinions into a single one. In this paper, a new method is given to integrate these experts′ views to a single one. Lastly, a numerical example is used to demonstrate the proposed approach.

Key words:system reliability, experts′ opinions, fuzzy probability, coincidence degree

文章编号：1007-4260(2015)03-0038-04

中图分类号：O231. 2

文献标识码：A

DOI：10.13757/j.cnki.cn34-1150/n.2015.03.011

通讯作者：汤胜道，男，安徽马鞍山人，博士，安徽工业大学数理科学与工程学院副教授，研究方向为可靠性理论与应用。

作者简介：张鑫，男，安徽芜湖人，安徽工业大学数理科学与工程学院硕士研究生，研究方向为模糊可靠性。

收稿日期：2014-10-25

网络出版时间：2015-8-25 15:40网络出版地址：http://www.cnki.net/kcms/detail/34.1150.N.20150825.1540.011.html