舰载武器捷联惯导系统极地传递对准算法

郭元江，钱 江，徐海刚，李海军，刘 冲

(1.北京自动化控制设备研究所，北京 100074；2.海装舰艇部，北京 100084)



舰载武器捷联惯导系统极地传递对准算法

郭元江1，钱 江2，徐海刚1，李海军1，刘 冲1

(1.北京自动化控制设备研究所，北京 100074；2.海装舰艇部，北京 100084)

针对我国海军舰载武器捷联惯导系统的极地作战环境适应性问题，分析了武器惯导在极区条件遇到的两大挑战：极区航向输出与高精度对准问题。对于极区导航问题，在导航解算中设定不重合于地理系的格网导航坐标系以解决航向输出难题；对于高精度对准问题，也提出了格网导航系下的“速度+姿态角速率”匹配传递对准解决方案。最后通过模拟仿真舰艇极地航行条件，验证了格网导航以及传递对准方法在极地条件的适用性。

捷联惯导；极地导航；格网导航；传递对准

0 引言

目前，我国逐渐开始加入北极资源合作开发中，因此为保护我国在北极活动中的经济利益，提升在北极事务中的话语权，需开展武器装备系统极地特性的研究工作，尤其是海军武器装备系统。

我国现役海军舰载武器系统及各分系统设计时，不特别考虑极区环境使用条件。当导弹武器系统工作在极地地区，高纬度、低温、复杂磁场等工作条件的变化可能会对舰载武器，包括武器导航系统产生影响。例如卫星导航系统由于卫星分布原因，在两极和高纬度地区的部分区域可能出现卫星覆盖空洞，这将可能使接收到的卫星几何分布不理想，导航精度有所降低[1]。

惯导系统具有高自主性、可靠性与隐蔽性等特点，是舰载武器系统中重要的导航设备。目前舰载武器中的捷联惯导系统在极区环境下同样存在使用风险，如极点航向输出、极区高精度对准等问题[2]。因此，国内惯性技术研究所与高校相继开展极区惯性导航问题研究。航空618所研究了极地飞行的导航算法以及机载武器传递对准算法[3-4]；西北工业大学、海军工程大学等院校也对相关技术进行了初步研究。但是，在舰载武器惯导快速对准方面，目前国内尚无相关研究成果。

本文将针对舰载武器极地快速对准问题，提出相应解决方法。其中在第1节中分析极区条件对现有舰载武器惯导系统的影响；在第2节中提出适用于极区条件的格网导航算法；第3节中提出适用于舰载条件的格网导航系下“速度+姿态角速率”匹配传递对准方法；第4节中完成导航与传递对准仿真分析，以验证该方案在极地的可适用性。

1 极区条件惯导系统影响分析

极区环境对舰载武器惯导系统的影响包括两部分：极地条件对惯性导航影响；极地条件对惯导对准影响。本文将对以上两方面影响分别进行分析。

1.1 惯导导航影响分析

指北方位机械编排方式的导航算法中，数学平台的角速度指令为：

(1)

采用指北方位机械编排时，在计算给惯性平台或数学平台指令的角速度中，需要使用secL项。这一项在高纬度地区会变得很大，尤其在极点该项变为无穷大，使得导航计算溢出。可见，在极地地区受高纬度的影响，现役海军导弹武器系统中惯导的指北方位机械编排方式会受到制约，导航系统不能正常工作。

1.2 惯导对准影响分析

武器惯导采用的“速度匹配”对准方法通过罗经效应实现方位对准。罗经效应下的航向对准误差φu为[5]

(2)

式中，εe为惯导系统的等效东向陀螺漂移；ωie为地球自转角速度；L为纬度。

图1为陀螺漂移为0.01(°)/h的惯导在纬度为0～75°范围内对应的“速度匹配”航向对准精度曲线。由图1可知，在纬度为75°时，“速度匹配”的航向对准误差为18.9′(3σ)，而在纬度为40°时，对准航向误差仅为8.5′(3σ)。

图1 不同纬度惯导自对准航向误差曲线Fig.1 The results of heading alignment at different latitude

可见，随着惯导所处纬度的升高，其航向对准精度也大幅降低。尤其在高纬度的极地地区，武器惯导采用罗经方式对准的精度会大大下降，而在极点附近甚至无法进行罗经航向对准。另外，“姿态匹配”会使用基准惯导的指北航向信息，但是在极点位置无指北方位角，因此“姿态匹配”传递对准方法也无法完全保证在极区的正常工作。所以这将极大影响舰载武器捷联惯导系统的对准精度，限制舰载武器的使用环境。

2 极地导航算法

指北惯性导航在极区应用的主要问题是测量方向精度下降，甚至在极点无法提供航向信息。因此通过引入虚拟航向来解决航向输出问题。本文将采用格网方位导航编排方法。

格网导航坐标系(G)以所在地P点处平行于格林尼治子午面的平面作为格网平面，以所在地的水平面作为切平面。格网平面与切平面的交线定义为格网北向，其中格网北向同真北方向的夹角为σ；格网天向同地理天向重合；格网东向在切平面内且与格网北向垂直以构成右手直角坐标系，如图2所示[6-7]。

图2 格网坐标系定义示意图Fig.2 The schematic diagram of grid coordination

(3)

格网导航算法的姿态更新、速度更新以及位置更新方法与指北导航算法类似，即

(4)

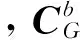
(5)

3 极地传递对准算法

目前，导弹武器导航系统的传递对准方案包括位置匹配对准、速度匹配对准、加速度匹配对准、姿态匹配对准、角速度匹配对准，以及各种匹配的组合方式对准等。由于在极点附近地理经线收敛，无指北方位角，因此对于武器惯导系统，基于罗经效应的速度匹配无法工作，而姿态匹配中不能提供指北方位角信息，也不可工作。因为格网航向并不会在极点附近奇异导致计算溢出，因此考虑利用主子惯导的格网速度与格网姿态角速度误差作为量测信息，实现子惯导的传递对准。因此本文提出一种“格网速度+姿态角速率”匹配传递对准方法。

3.1 系统状态方程

选取子惯导格网速度误差δVG，格网姿态误差φG，加表零偏，陀螺漂移ε，主子惯导间安装误差角μ，弹性变形角θf和弹性变形角速率ωf作为状态量，即

其中，速度误差方程为

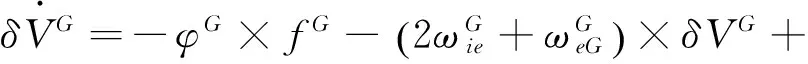
(6)

姿态误差方程为

(7)

加表零偏误差方程为

(8)

陀螺漂移误差方程为

(9)

弹性变形角误差模型为

(10)

弹性变形角速率误差模型为

(11)

式中，β=1/τ，τ为三个轴向变形角的相关时间。

利用上述误差方程可构建卡尔曼滤波系统状态方程

(12)

3.2 系统量测方程

(1)格网速度量测方程

格网导航系下子惯导速度与基准速度信息之差可作为格网速度量测值，即格网速度的量测方程为

(13)

量测信息为

z1=VsG-VmG

(14)

式中，VsG、VmG分别为子、母惯导的格网速度。

(2)姿态角速率量测方程

(15)

其中，(μ×)为μ的反对称矩阵，(θf×)为θf的反对称矩阵。考虑到运载体动态变形角速度的影响，主、子惯导系统测量的角速度之间的关系如下

(16)

可以得到

(17)

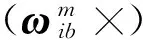
(18)

因此

(19)

上述的推导主要考虑的是主、子惯导间由于安装误差角、弹性变形角引起的角速度输出差异，然而实际上，子惯导惯性器件存在误差(传递对准中假设主惯导无误差)，主要是陀螺漂移直接在上述误差因素基础上，额外增加了子惯导角速度的输出。因此，实际的主、子惯导角速度差还要考虑子惯导陀螺漂移的影响，于是

(20)

因此，角速率匹配的量测矩阵为

(21)

量测信息为

(22)

综上可得，系统的量测方程H为

(23)

量测信息z为

z=[z1z2]T

(24)

4 仿真分析

4.1 导航仿真

为验证极区格网导航算法的合理性，设定舰艇沿着经线向北穿越极点然后驶出极区的航迹。在仿真过程中设置仿真参数如下：

1)初始方向：正北；

2)载体速度：20节；

3)初始位置：北纬89°，东经116.15326°；

4)到达极点之后，继续前行，沿着西经63.84674°经线向南航行。

另外，在导航仿真中加入以下误差项：

1)三轴陀螺漂移0.01(°)/h；

2)三轴加表零偏0.1mg；

3)初始航向误差为0.05°。

图3 导航结果Fig.3 The results of grid navigation

图3为位置误差、格网速度、水平姿态角和格网航向角的导航仿真结果，可见格网导航算法可正常工作在地球极点处，不会存在计算溢出的问题。由图3可知，姿态、速度和位置的误差变化特性与传统导航算法误差特性相同，同样有舒拉周期与地球周期，可见解算导航系的变化并不会对导航误差特性产生影响。但是格网航向的变化与传统航向变化不同，它并不存在地球周期，而是发散。这是由于格网航向相当于格网航向与地理航向夹角σ与地理指北航向的叠加，其中格网航向与地理航向夹角σ为

σ=tan-1(-sinLtanλ)

(25)

所以σ误差与地理位置以及位置误差相关。因此，虽然地理航向误差仍然具有地球周期与舒拉周期，但是格网航向误差会随纬度误差变化而逐渐发散。

4.2 对准仿真

为了验证本文提出的格网“速度+姿态角速率”匹配传递对准方法，将在不同纬度条件分别进行仿真。仿真条件为：

图4 纬度为45°时的安装误差角与陀螺漂移估计值Fig.4 The estimate of installation error and drift at N45°

1)纬度：45°和89.99°；

2)舰艇晃动角度：滚转、航向与俯仰均为0.5°sin(2πt/20)；

3)母子惯导安装误差角：-0.2°,0.18°,-0.2°；

4)武器惯导陀螺漂移：1.0(°)/h；

5)武器惯导加表零偏：0.1mg。

不同纬度下格网“速度+姿态”匹配的安装误差角与陀螺漂移估计值分别如图4和图5所示。可见，在不同纬度下估计结果类似，对准效果相当。所以该传递对准方法除适用于极地以外，还适用于中低纬度条件。

图5 纬度为89.99°时的安装误差角与陀螺漂移估计值Fig.5 The estimate of installation error and drift at N89.99°

5 结论

本文从我国海军舰载导弹捷联惯导系统在极地作战环境适应性出发，分析了舰载武器惯导在极区条件遇到的两大挑战：极区航向输出问题与高精度对准问题。针对极区导航问题，在导航解算中采用格网方位编排方式，通过设定不重合于地理系的导航坐标系以解决航向输出问题；针对武器惯导对准问题，提出采用格网系下“速度+姿态角速率”匹配传递对准方法实现快速、高精度对准。最后通过模拟仿真舰艇极地航行条件，验证了格网导航以及格网“速度+姿态角速率”匹配对准方法在极地条件的适用性。

[1]GaoXX,HengL,WlterT,etal.Breakingtheice:navigatinginthearctic[C] //.Proc.ofthe24thInternationalTechniacalMeetingoftheSatelliteDivisionoftheInstituteifNavigation, 2011:3767-3772.

[2]IgnagniMB.All-EarthInertialNavigationScheme[J].Navigation, 1972, 19(3) : 209-214.

[3] 周琪,秦永元,严恭敏,岳亚洲.极区飞行格网惯性导航算法原理[J].西北工业大学学报,2013.4(31)2:210-217.

[4] 吴枫,秦永元,周琪.机载武器极区传递对准算法[J].中国惯性技术学报,2013.4(21)2:141-146.

[5] 秦永元.惯性导航[M].北京:科学出版社,2006.

[6]SmuelHerrick.GridNavigation[J].GeographicReview, 1944, 34(3) : 135-147.

[7]KendallEC.Gyro/GridNavigation[J].JournalofNavigation, 1956, 9(4) : 429-435.

Inertial Navigation System of Ship Weapon Transfer Alignment Algorithm in the Polar Regions

GUO Yuan-jiang1, QIAN Jiang2,XU Hai-gang1, LI Hai-jun1, LIU Chong1

(1.Beijing Institute of Automatic Control Equipment,Beijing 100074,China；2.Naval Equipment Department,Beijing 100084,China)

The strap-down inertial navigation system (INS) for ship weapon faces two problems in the polar regions, and the problems make that the INS for missile of naval ships is disable. At the polar point of the earth, it is difficult to establish the heading. To solve the problem, the grid coordinate frame is presented, and the grid mechanization equations and error equations are derived by using the technique. The rapid and high precision transfer alignment also effects the ability of naval ships missile. In the grid coordinate frame, the velocity and angular rate matching Kalman filter is designed to estimate and correct the INS’s velocity, attitude and inertial sensor errors. Finally, the simulation results show the navigation and transfer alignment algorithm makes the INS for missile of naval ships can be used in the polar rigions.

Strap-down inertial navigation; Polar navigation; Grid navigation; Transfer alignment

2015 - 03 - 10；

2015 - 03 - 10。

郭元江(1986 - )，男，助理工程师，主要从事惯性导航方面的研究。

E-mail: harbor35030324@163.com

U666.1

A

2095-8110(2015)03-0023-06