基于终端滑模的直接力/气动力复合控制系统设计
赵玉杰,廖志忠,段朝阳,张公平
(中国空空导弹研究院, 河南 洛阳 471009)
基于终端滑模的直接力/气动力复合控制系统设计
赵玉杰,廖志忠,段朝阳,张公平
(中国空空导弹研究院, 河南 洛阳 471009)
针对空空导弹直接力/气动力复合控制问题,建议一种基于非奇异快速终端滑模控制方法(NFTSM)和动态控制分配技术的复合控制策略。根据导弹纵向运动模型设计非奇异快速终端滑模控制器,获得建立导弹过载所需要的控制力矩。采用动态控制分配将期望的控制力矩映射到气动舵和直接力装置。仿真结果表明,提出方法适用于空空导弹直接力/气动力复合控制系统设计,能够快速精确跟踪过载指令。
直接力/气动力复合控制;非奇异快速终端滑模;动态控制分配;控制力矩
0 引言
传统空空导弹利用空气舵偏转产生气动控制力矩改变导弹姿态,进而建立攻角,依靠气动升力产生导弹过载。随着具备隐身、高机动、超声速巡航能力的空中威胁大量涌现,未来战场环境更加复杂多变,从而对新一代空空导弹提出更严峻的挑战。单纯依赖气动舵产生气动控制越来越难以应对未来的作战环境。为提高空空导弹的作战能力,改善导弹的响应特性,空空导弹引入姿控式直接侧向力与气动舵形成复合控制,从而快速改变导弹姿态。
对于直接力/气动力复合控制系统设计问题,国内外学者已做了大量研究工作[1-3],但这些设计方法大多建立在精确的数学模型基础上。直接力装置的引入,带来了侧向喷流干扰效应,复杂的工作环境使得复合控制系统难以精确建模,同时执行机构具有不同动态特性,彼此间的协调也成为直接力/气动力复合控制系统设计所面临的主要问题。传统的设计方法与设计理念将很难实际解决复合控制系统设计问题。滑模控制具有响应快,对参数摄动外部扰动不变性等优点,特别适用于非线性不确定系统。传统滑模系统状态到平衡点的收敛是渐近的,终端滑模系统状态能在有限时间收敛至平衡点,具有更高稳态精度。普通的终端滑模设计方法中存在奇异问题,冯勇等提出一种非奇异终端滑模控制,使控制律无负指数项,但在远离平衡点处收敛缓慢,并且系统仍存在抖振问题[4]。李升波等针对二阶不确定非线性系统,提出一种非奇异快速终端滑模控制方法,设计非奇异快速终端滑模面,采用新的滑模趋近律,既解决终端滑模奇异性问题,又解决滑模控制收敛缓慢和抖振问题[5]。
本文以末制导段空空导弹为研究对象,通过建立过载控制数学模型,并作一定变换,设计了一种非奇异快速终端滑模控制和动态控制分配技术相结合的复合控制策略,实现对导弹过载的快速精确跟踪。
1 复合控制系统数学模型
1.1 弹体动力学模型
直接力/气动力复合控制空空导弹采用直接力位于质心后的姿控方式,弹体配置方式如图1所示。
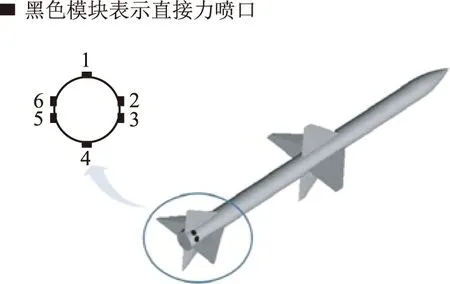
图1 姿控式复合控制空空导弹弹体配置Fig.1 The structure of the air-to-air missile with blended control
为了便于说明控制系统设计过程,只考虑导弹末制导段在纵向平面的姿态控制问题,将导弹的质量和速度视为常值,建立导弹姿态运动的数学模型,如式(1)~式(3)所示。
(1)
(2)
(3)
其中,α为导弹攻角,ωz为俯仰角速率,ny为导弹过载,δz为升降舵偏角,fy为侧喷发动机产生的直接力。a1、a2、a3、a3′、a4、a5、a5′为动力学系数,其中a3′=-l/jz,a5′=1/mV,jz为转动惯量,l为侧喷发动机到质心距离,m为导弹质量,V为导弹飞行速度。
设虚拟控制输入σ为控制力矩
σ=Wu
(4)
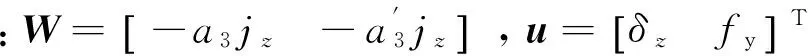
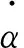
(5)

(6)
其中
式中Km为导弹传递系数,单位为s-1;Tm为导弹时间常数,单位为s;ξm为导弹相对阻尼系数,量纲为1。

(7)
1.2 执行机构数学模型
气动舵数学模型描述为如下二阶系统
(8)
直接力装置数学模型描述为如下一阶系统
(9)
式中:
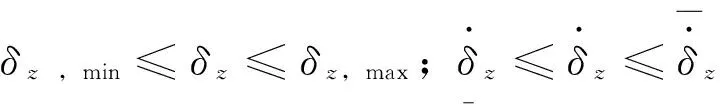
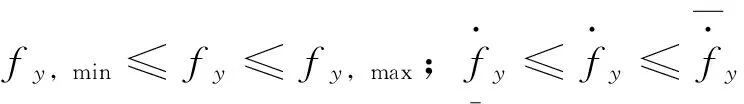
ωδ,ξ分别为舵系统无阻尼自振频率和阻尼比;
δz,min,δz,max分别为舵偏转角的下界与上界;
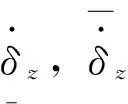
fy,min,fy,max为直接力装置推力的下界与上界;

2 复合控制设计
直接侧向力/气动力复合控制主要目的是实现过载快速精确跟踪。设计非奇异快速终端滑模控制律,得到期望的控制力矩,通过动态控制分配技术将控制力矩分别映射到气动舵系统和直接力系统,操纵导弹改变姿态,控制导弹运动。系统结构如图2所示。

图2 复合控制策略Fig.2 The blended control strategy
2.1 非奇异快速终端滑模方法
对于如下二阶系统
(10)

(11)
式中κ∈R+,υ∈R+,p,q,g,h为奇数,要求满足1
p/q以保障滑模面的非奇异性,采用一种带负指数项的终端吸引子设计趋近律
(12)
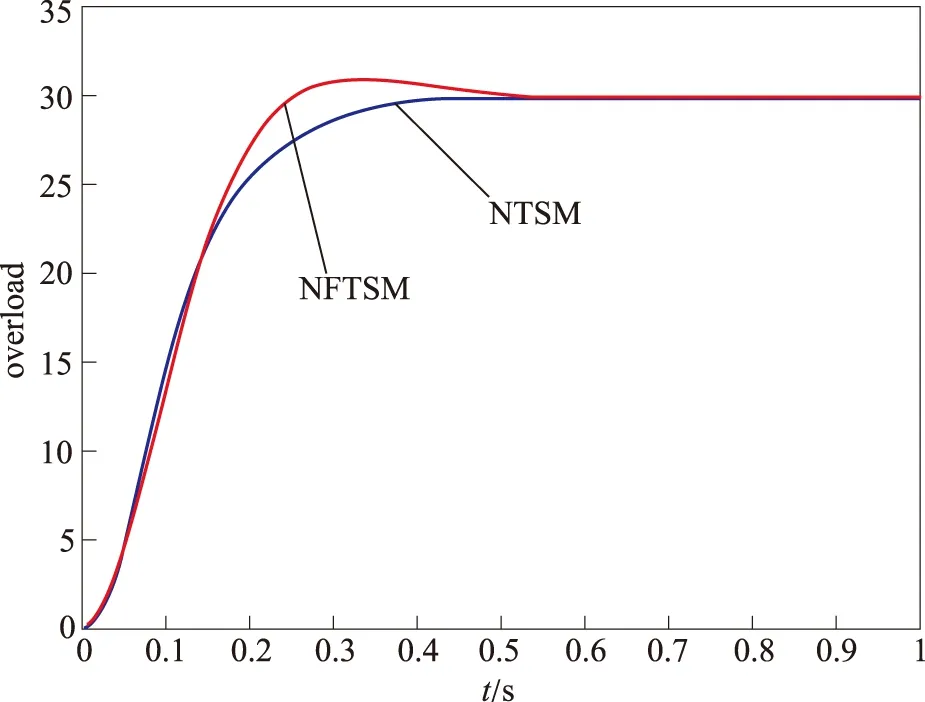
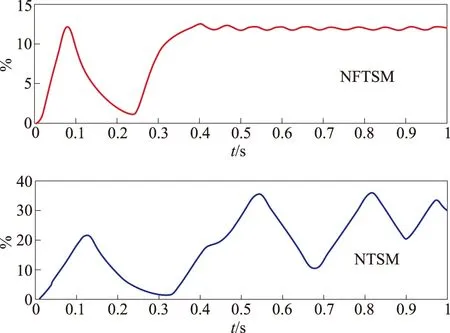
其中φ∈R+,γ∈R+,m,n∈N为奇数,要求满足0 (13) 由于1 1,所以式(13)中状态变量x1,x2的指数皆大于零,无负指数项,这说明基于滑模面(11)和趋近律(12)设计的控制方法完全避免奇异问题,且控制律时间连续,无抖振。系统状态有限时间收敛,收敛时间 (14) 其中: 2.2 复合控制系统过载跟踪控制器设计 (15) 非奇异快速终端滑模面设计为 (16) 控制律 (17) 2.3 动态控制分配设计 如式(8)~式(9)所示,直接力/气动力复合控制空空导弹有两种不同的执行机构,即直接力装置和气动舵。为了达到快速建立过载的目的,需要对这两种执行机构进行协调控制,一般采用分配的方法来实现。但目前大多数分配方法属静态分配,没有考虑执行机构的动态特性。这将严重影响分配精度和控制系统系统性能。在动态分配的优化指标中,额外考虑由执行机构动态特性引起的时间延迟,在考虑位置和速率饱和约束条件下,使执行机构实际产生的控制作用与期望的总的控制作用近似相等[6]。 气动舵偏角和偏转角速率约束以及直接力推力和速率约束如下: (18) (19) 速率约束也可看成位置约束形式 (20) 由式(18)~式(20),将气动舵与直接力的组合饱约束写为 (21) 将控制分配问题转化为一个受约束二次型规划问题[7]: Bu(t)-v(t)=0 Cu(t)-U≥0 (22) 图3 过载随时间变化曲线Fig.3 Curve of the change of overload 图4 舵偏角随时间变化曲线Fig.4 Curve of the change of actuator deflection 图5 直接力随时间变化曲线Fig.5 Curve of the change of reaction-jet 图6 过载随时间变化曲线Fig.6 Curve of the change of overload 图7 舵偏角随时间变化曲线Fig.7 Curve of the change of actuator deflection 图8 直接力随时间变化曲线Fig.8 Curve of the change of reaction-jet 图3~图5为未考虑执行机构位置、速率约束和动态特性时的仿真结果。可以看出,NFTSM系统与NTSM系统过载响应时间均约为0.1s,但前者具有更快的过载跟踪速度;NTSM系统舵偏角指令与直接力指令均存在严重抖振现象,且舵偏角已明显超出气动舵最大偏转角。图6~图8为考虑执行机构位置、速率约束和动态特性并采用动态控制分配策略的仿真结果,可以看出NTSM系统由于控制输入指令存在严重抖振,在考虑执行机构位置、速率约束时,气动舵与直接力装置难以产生相应的舵偏角和直接力,因此无法实现对过载的精确跟踪。NFTSM系统控制输入平滑无抖振,通过与动态控制分配策略相结合,既考虑了气动舵和直接力装置的位置、速率约束和动态特性,又能实现对过载的快速精确跟踪。图9为所设计复合控制系统存在d=1000sin(100t)Nm的干扰力矩,并且气动参数分别向上和向下摄动50%时的仿真曲线,可以看出,当存在参数摄动和外部扰动时,复合控制系统仍然能够实现对过载的快速精确跟踪,说明所设计复合控制系统品质良好,具有很强的鲁棒性。 图9 过载随时间变化曲线Fig.9 Curve of the change ofoverload 针对空空导弹的复合控制问题,提出一种基于非奇异快速终端滑模和动态控制分配技术的复合控制策略。非奇异快速终端滑模方法适用于存在参数摄动及外部扰动大的系统并具有较快的跟踪误差收敛速度;动态控制分配技术在基于执行机构位置速率约束的基础上考虑执行机构动态特性对控制量进行分配,仿真结果表明,依靠二者的协调控制,既可以实现过载的快速精确跟踪,又可以改善空空导弹的响应特性。 [1]KevinAWise,SavidJBroy.AgileMissileDynamicandControl[J].JournalofGuidance,Control,andDynamics,1998,21(3). [2]KMenon,VRIragavarapu.Adaptivetechniquesformultipleactuatorblending[C]//.AIAA-98-4494, 1998. [3]WANGYu-hang,YAOYu,BIYong-tao.LateralThrustandAerodynamicsBlendedControlSystemDesignBasedonAutoDisturbanceRejectionController[J].JournalofAstronautics,2009,30(4):1544-1550. [4]FengY,YuX,ManZ.Non-singularAdaptiveTerminalSlidingModeControlofRigidManipulators[J]. 2002, 38(12):2159-2167. [5] 李升波,李克强,王坚强,等. 非奇异快速的终端滑模控制方法 [J]. 信息与控制, 2009, 38(1):1-8. [6] 毕永涛,贺风华,姚郁. 敏捷导弹直接侧向力与气动力复合控制策略 [J]. 吉林大学学报,2011, 41(2):590-596. [7]RidgelyDB,DrakeD,TriplettI.Dynamiccontrolallocationofamissilewithtailsandreactionjets[C]//.AIAA,SouthCarolina,American, 2007. [8]OlaHarkegard.DynamicControlAllocationUsingConstrainedQuadraticProgramming[J].JournalofGuidance,Control,andDynamics,2004,27(6):1028-1034. Design of Blended Lateral Thrust and Aerodynamic Control System Based on Terminal Sliding Mode ZHAO Yu-jie, LIAO Zhi-zhong, DUAN Chao-yang, ZHANG Gong-ping (China Airborne Missile Academy,Luoyang 471009,China) A control strategy is proposed for the air-to-air missile with the blended lateral thrusters and aerodynamic surface control based on the nonsingular fast terminal sliding mode control(NFTSM) and the dynamic control allocation. A NFTSM controller is designed using the longitudinal dynamic model of the air-to-air missile to obtain the control moments required by the overload of the missile. The required control moments are mapped into the respective control commands on the aerodynamic deflector and the thrust engine array using the dynamic control allocation to realize the fast and the accurate tracking of the overload of the missile. The proposed blended control strategy can fast track the overload command accurately, proving a basis for the design of air-to-air missile with lateral thrust and aerodynamic control. Blended lateral thrust and aerodynamic compound control; Nonsingular fast terminal sliding mode; Dynamic allocation;Control moment 2014 - 11 - 16; 2015 - 01 - 10。 赵玉杰(1990 - ),男,硕士研究生,主要从事导航制导与控制方面的研究。 E-mail: zhaoyujie9009@163.com TJ765.2 A 2095-8110(2015)03-0049-06


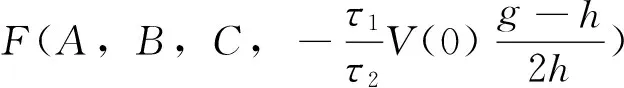

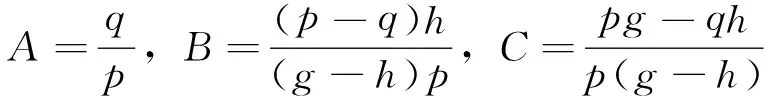

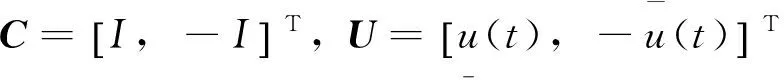
3 仿真结果及分析






4 结论

