旋转导向系统井身轨迹旋转测量方法研究
郭秋芬,岳步江,刘庆成,马慧斌,陈大琪
(1.航天科工惯性技术有限公司,北京 100074;2.中国石油川庆钻探钻采工程技术研究院,四川 广汉 618300)
旋转导向系统井身轨迹旋转测量方法研究
郭秋芬1,岳步江1,刘庆成1,马慧斌1,陈大琪2
(1.航天科工惯性技术有限公司,北京 100074;2.中国石油川庆钻探钻采工程技术研究院,四川 广汉 618300)
通过分析旋转导向过程中对系统及其系统内各个分部件的影响,建立了旋转导向井身轨迹旋转测量方法的数学模型。针对理论分析,建立了Matlab 仿真模型,并进行了仿真图形分析。最后,进行了试验验证,给出试验结果。从整个试验过程和试验结果可以证明所研究的测量方法是正确并可行的。
旋转导向;旋转测量;测量方法;数学模型;仿真;试验验证
0 引言
旋转导向技术是当前钻井技术中的一项自动化钻井新技术,从20世纪80年代国外研究机构开始进行研究,90年代初期形成了商业技术。旋转导向系统与其他随钻系统相比,最大的优点在于旋转的状态下实现井眼轨迹的实时导向,改变了定向井技术在控制井眼轨迹上的传统作业方式。采用钻井的这一高新技术不仅可以提高钻井成功率、减少事故,并且可以从整体上降低钻井成本[1-2]。旋转导向钻井在作业效率和作业安全方面取得了突破性进展,尤其是在海上大位移钻井技术中发挥了显著优势[3-4]。但是,如何在旋转导向方式下实时精确地测量出系统的井眼轨迹参数是整个旋转导向系统的技术难点之一。在非旋转导向的方式下,由于导向工具上部钻柱不旋转,因而比较容易解决测量单元测量功能和测量精度的问题。在旋转导向方式下,旋转的钻柱给测量系统带来旋转角速度等误差源,增加了测量难度。因此,在旋转导向钻井系统中,如何保证轨迹测量系统的测量精度,获得精确的井眼轨迹是旋转导向钻井系统的关键技术之一。
1 组成
旋转导向钻井系统主要由地面部分、井下部分和测试设备组成。地面部分主要完成指令下传、井身姿态测量、井下数据的接收和显示相关工程参数。井下部分主要完成井下参数测量、轨迹控制、地面指令接收和井下数据上传。测试设备主要完成各个主要部件的功能测试。井下部分包括旋转导向工具、挠性短节、中控和随钻测量(MWD)系统。旋转导向系统的关键技术之一就是在旋转状态下能够测量出井眼轨迹参数,其测量系统包括近钻头测量系统和随钻测量(MWD)系统。
本文主要研究的是井身轨迹测量单元,组成如图1所示,能够实时测量系统的井眼轨迹参数,为旋转导向系统钻井提供基础的技术参数依据。

图1 旋转导向系统井身轨迹测量单元组成图Fig.1 Composing of rotary steering drilling system
2 测量原理及模型
旋转导向系统的井眼轨迹参数主要由井斜角、方位角和工具面角组成。要想得到这3个参数,首先规定坐标系和各个参数的代表符号。地磁坐标系m系和载体坐标系b系,井斜角为θ,方位角为φ,工具面角为γ,如图2所示。图中Xm轴指向磁北、Zm轴指向地(Zm与地垂线重合),Ym方向与Xm、Zm形成右手坐标系。Xb轴沿着载体的周向指向弧形连接面的方向,Zb轴沿轴向指向靠近钻头的方向,Yb轴与Xb、Zb形成右手坐标系。

图2 坐标系定义及角度定义示意图Fig.2 Definition of coordinates and angles
2.1 静态输出姿态角
旋转导向系统输出的姿态角分别为井斜角θ、方位角φ、高边工具面角T、磁性工具面角ξ。井斜角θ指Zb轴与Zm轴的夹角,定义域为0°~180°;方位角φ指Zb轴在水平面(XmOYm形成的平面)的投影与Xm轴之间的夹角,逆时针为增大方向,定义域为0°~360°;工具面角γ在不同的井斜角的情况下分为两种:高边工具面角T和磁性工具面角ξ,高边工具面角T指Xb轴与高边面(高边面:载体圆周上离地面最近的一条母线与载体中心线形成的矩形面)之间的夹角,逆时针为增大方向,定义域为0°~360°;磁性工具面角ξ指Xb轴在水平面的投影与Xm轴之间的夹角,定义域为0°~360°。

(1)
根据坐标变换和转换矩阵表达式(1),得到井斜角的表达式如式(2)所示
(2)
其中aib(i=x、y、z)为载体坐标系加速度计的输出,g。
从式(2)可以看出,表达式与3个加速度计的输出都相关联,因此,需要得到加速度计的精确输出,才能获得精确的姿态角。
3个加速度计和3个磁通门传感器的输出表达式如式(3)、式(4)所示。


(3)
式中:Vai(i=x、y、z)为加速度计的输出电压,V;Vai0(i=x、y、z)为加速度计的零偏,V;Kai(i=x、y、z)为加速度计的标度因数;Kaij(i=x、y、z,j=x、y、z)为加速度计的安装误差系数;dai0(i=x、y、z)为加速度计的系统偏差,ai(i=x、y、z)为加速度计敏感到的加速度,g。



(4)
式中:Vmi(i=x、y、z)为磁通门的输出电压,V;Vmi0(i=x、y、z)为磁通门的零偏,V;Kmi(i=x、y、z)为磁通门的标度因数;Kmij(i=x、y、z,j=x、y、z)为磁通门的安装误差系数;dmi0(i=x、y、z)为磁通门的系统偏差,ai(i=x、y、z)为磁通门敏感到的磁场强度,Gs。
即得到静态下加速度计和磁通门的物理量输入表达式如式(5)、式(6)所示:
(5)
(6)
2.2 旋转状态下的算法
旋转导向系统的特点之一是在钻进过程中不停,在钻进过程中进行姿态测试,进行导向。而之前的钻井系统都是钻进过程中,停止一段时间,进行姿态测试,测试之后再进行钻进。为了适应钻进过程中进行姿态测试,必须对算法做进一步的研究。
在旋转过程中,产生误差的因素较多,主要因素是向心加速度。磁通门的工作原理是利用软磁材料被激励时的特性,没有或者较弱磁场环境下,磁通门的感应线圈输出的电动势只包括激励电流的奇次谐波,当存在与敏感方向平行的环境磁场时,由于磁导率的变化使得输出中不仅包含激励电流的奇次谐波,还包含激励电流的偶次谐波,且偶次谐波的幅值正比于平行轴向方向的磁场分量。为了提高测量精确度,一般采用差分输出,此时激励电流产生的奇次谐波能被抵消,而由于环境磁场所产生的偶次谐波则叠加。由此可以看出,磁通门的输出不包括加速度项,因此,磁通门的输出表达式不变,仍如式(6)所示。
加速度计的工作原理是敏感摆片上的加速度,当加速度计的敏感质点与系统的旋转轴同心时,系统旋转就不会产生向心加速度,使得输出中不包含向心加速度项,但是系统加工以及安装过程中,加速度计的敏感质心与系统的旋转轴向并不重合。当系统旋转时,由于敏感质心与系统转动轴之间的间距,会产生向心加速度,此现象称为 “尺寸效应”。以往的随钻系统都是在静态下测量姿态,姿态算法中加速度计的输出模型中不包括向心加速度项,而在旋转导向系统中,需要在旋转状态下测量姿态,因此需要建立向心加速度对加速度计的影响模型,达到系统对姿态角的要求。
将旋转项加入传感器的输出表达式中,根据式(1)、式(3)、式(4)、式(5)和式(6),得到测量单元转动情况下加速度计的输出表达式如式(7)、式(8)所示。
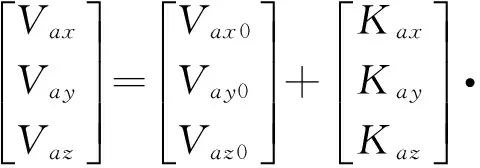



(7)

(8)
式中,ω为旋转角速度,rad/s。
3 仿真分析
根据式(2)可得到井斜角误差表达式如式(9)所示。
(9)
式(9)是根据倒数及舍掉小量的计算方法得到的,计算出的数值比式(2)直接计算出的井斜角与静态井斜角相减得到的误差值要小一些。
根据向心加速度的公式,得到旋转情况下,加速度计的输出误差仿真图形如图3所示。
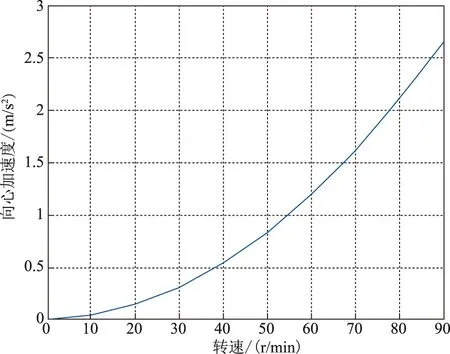
图3 向心加速度与转速的关系图形Fig.3 Relationship of the Acceleration Centripetal and the Rotate Speed
从图3中可以看出,当转速为80r/min时,产生的向心加速度为2.1m/s2(即0.214g),即每个方向向心加速度误差最大达到了21.4%。
根据上述算法,在MATLAB中对其进行误差仿真分析。具体计算方法如下:
斜度定为15°,加工线性误差定为0.03mm,转速分别设定为1.2r/min、5r/min、20r/min、50r/min、60r/min、90r/min,将旋转向心加速度误差加入加速度计的输出中,根据式(2)得到静态井斜角和动态井斜角,误差仿真图形如图4所示。

图4 井斜角误差与时间的关系图(加入转速后井斜角与没有加入转速的井斜角相减)Fig.4 Relationship of the error of the angle of the well and the time (the minus of the angle of the well adding rotate speed and the angle of the well no rotate speed)
从图4中可以看出,井斜角误差是随着时间发生周期性变化的,并且随着转速的增加而增加。
根据式(10),得到误差仿真图形如图5所示。

图5 井斜角误差与时间的关系图(误差公式(13))Fig.5 Relationship of the angle of the well and the time (error formula (13))
从图5中可以看出,根据式(9)计算出的误差与根据式(8)代入式(2)得到的误差随时间变化的规律是相同的,但是数值的大小不同。这与式(9)舍掉小量的计算方式有关,与理论分析是相符的。
4 试验验证
经过仿真分析可以看出,仿真结果与理论分析是相符的,为了验证理论,进行试验验证。
4.1 磁通门试验验证
在旋转过程中,通过试验验证了旋转状态下对磁通门的输出基本没有影响,测试数据图形如图6所示。

图6 旋转时磁通门的输出Fig.6 Output of the fluxgate as rotating
从图6中可以看出,磁通门在转速在0~120r/min的情况下,输出绝对变化量小于60nT,相对变化量小于0.24%,变化量很小,因此磁通门的输出不需要进行补偿。
4.2 加速度计试验验证
在旋转过程中产生的向心加速度会对加速度计的输出有影响,具体测试结果如图7和图8所示,图中,data1为x轴,data2为y轴,data3为z轴。

图7 输入角速度的平方与输出加速度的关系图Fig.7 Relationship of the square of the input angle rate and the output acceleration

图8 输入角速度的平方与输出加速度误差的关系图Fig.8 Relationship of the square of the input angle rate and the output acceleration error
从图7和图8中可以看出,3个轴向的向心加速度都随着输入角速度增大而增大,向心加速度与角速度的平方基本成线性关系。在所测的测量系统中,x轴的向心加速度最大,y轴次之,z轴最小。
4.3 井斜角试验验证
井斜角试验验证结果如图9所示。
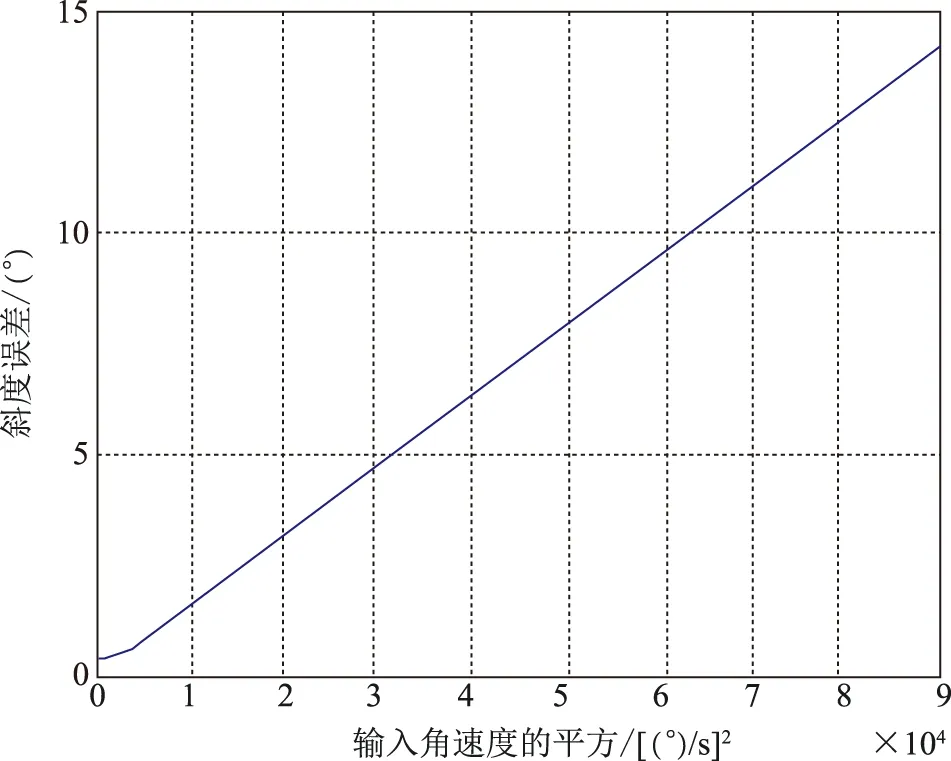
图9 输入角速度的平方与井斜角误差的关系图Fig.9 Relationship of the square of the input angle rate and the error of the angle of the well
从图9中可以看出,斜度误差与输入角速度基本成线性关系,当旋转速度为300(°)/s时,向心加速度带入斜度的误差达到14.2°,不管是正向转动还是负向转动,与旋转速度的关系基本相同,与理论分析一样。
4.4 新算法试验验证
通过不同转速情况下加速度计的输出,根据新算法,得到传感器输出加速度误差如图10所示。

图10 补偿后输入角速度的平方与输出加速度误差的关系图Fig.10 Relationship of the square of the input angle rate and the error of the output acceleration after compensating
从图10中可以看出,补偿之后,3个方向输出的加速度误差最大为3.748×10-4g,提高了传感器的输出测量精度。
补偿之后的斜度误差如图11所示。

图11 补偿后输入角速度的平方与井斜角误差的关系图Fig.11 Relationship of the square of the input angle rate and the error of the angle of the well after compensating
从图11中可以看出,旋转角速度补偿之后,斜度的误差很小,在0~300(°)/s的旋转速度下,补偿之后,向心加速度对斜度误差影响小于0.02°,精度比补偿前提高了很多。
5 结论
本文研究了旋转导向系统井身轨迹旋转测量方法,分析了旋转对测量的影响,并建立了模型,进行了仿真和试验验证。从研究的结果可以看出,旋转测量误差随着旋转速度的增加而增加,基本与旋转角速度的平方成正比。通过算法研究并进行试验,将旋转误差消除后,当旋转速度为300(°)/s时,旋转转速对旋转测量单元的输出精度影响从14.2°降低到了0.02°。值得说明的是:在文中并没有涉及如何在系统中测量转速的问题,这是研究旋转导向系统井身轨迹旋转测量的一个关键问题,需要在今后的工作中做进一步研究。
[1] 李琪,杜春文, 张绍槐.旋转导向钻井轨迹控制理论及应用技术研究[J].石油学报,2005,26(4):97-101.
[2]EdmondsonJohn,AbbottChris,DaltonClive,etal.Theapplicationofrotaryclosed-loopdrillingtechnologytomeetthechallengesofcomplexwellboretrajectoriesintheJaniceField[R].SPE/IADC59218, 2000: 1-12.
[3] 姜伟.大位移钻井技术在渤海QK17-2 油田开发中的应用[J].石油钻采工艺,2000,22(3):1-7.
[4] 姜伟.大位移钻井技术在渤海QHD32-6 油田的应用[J]. 石油钻采工艺,2001,23(4):1-6.
[5] 李汉兴,姜伟,蒋世全,傅鑫生. 可控偏心器旋转导向钻井工具偏心位移控制分析[J].2008,20(3):184-188.
[6] 闫文辉,彭勇,张绍槐.旋转导向钻井工具的研制原理[J].石油学报,2005,26(5):94-97.
Drilling Track Rotation Measurement Method Research of Rotary Steerable System
GUO Qiu-fen1, YUE Bu-jiang1,LIU Qing-cheng1,MA Hui-bin1, CHEN Da-qi2
(1.Aerospace Science and Industry Inertial Technology Co.,Ltd., Beijing 100074, China; 2.Drilling & Production Engineering Technology Research Institute Directional Drilling Company, Guanghan 618300, China)
In this paper, analyzing the influence replying on the system is because of the rotary of the rotary steering, the model of the rotary steering measurement method is built. And it validates the theoretic analyses by emulating. It gives the result of the examination by the test validating.
Rotary steering; Measurement for rotary steering; Measurement method; Mathematics model; Silllulation; Examination validation
2015 - 03 - 12;
2015 - 03 - 24。
郭秋芬(1975 - ),女,博士,高级工程师,主要从事石油钻井仪器和石油测井仪器研究。
E-mail:gqf9571@163.com
TE27
A
2095-8110(2015)03-0067-07

