高超声速滑翔飞行器再入轨迹在线生成算法设计
刘长龙 王 勇 肖 红 任 洋 王 征 宫 涛
1.空军工程大学航空航天工程学院,西安710038
2.空军装备研究院航空所,北京100076
3.93886部队,吉林通化135300
由于在增大射程、突破导弹防御系统和再入段具备机动能力等方面的优势,CAV(Common Aero Vehicle)被认为是实现远程快速精确打击和力量投送的具有广阔应用前景的再入飞行器[1]。考虑到实时性要求,增强高超声速滑翔飞行器自适应任务的能力和作战的灵活性,有必要研究在线轨迹生成技术。在线生成的线轨迹并不一定是最优解,但必须满足快速性要求和再入走廊约束条件[2]。传统RLV根据航程要求和状态约束,采用小横程假设在线生成二维参考轨迹(阻力-速度剖面),但降低了再入飞行器的部分横向机动能力[3]。Ping Lu等基于给定的攻角剖面,利用QEGC条件将再入走廊约束转化成倾侧角约束,通过搜索倾侧角特征参数和倾侧角反转点实现了三维轨迹在线生成[4-5]。
本文首先分析了高超声速滑翔式再入飞行器在线轨迹生成的基本问题和特点。以文献[4]为基础将CAV再入走廊约束转化成倾侧角约束。考虑临近空间大气密度模型和高超声速条件下的气动力模型不确定性对约束转化的影响,从而提高生成轨迹的可行性。为了提高再入制导的灵活性,可采用同时修正攻角和倾侧角的方式实现预测校正制导,分析了攻角摄动对约束转化的影响。然后,考虑地面威胁情况,结合航向角误差走廊法和禁飞圆切线法将再入轨迹扩展到三维。最后,基于CAV-H的数据,对三维轨迹在线生成算法进行了综合仿真,达到了预期效果。
1 再入轨迹生成问题
1.1 再入运动方程


1.2 再入走廊和轨迹生成问题
再入走廊的边界由驻点热流密度、过载、动压和准平衡滑翔边界4个因素构成[7]。
确定再入走廊需事先确定攻角曲线,采用如下参数化最优攻角方案[2]
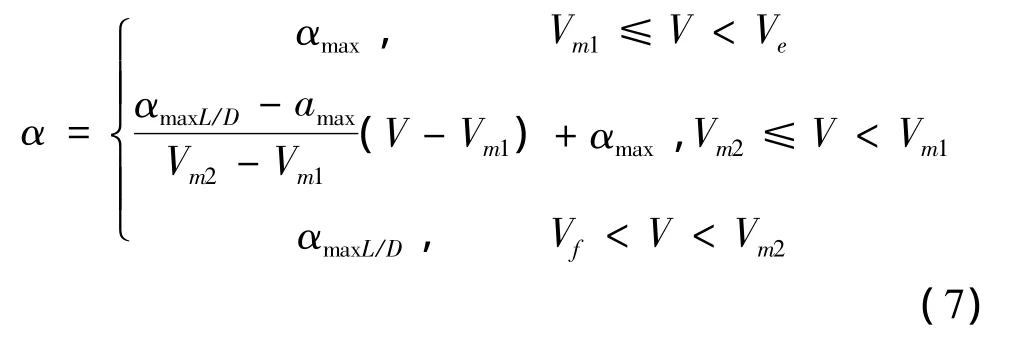
其中,Ve和Vf分别为再入点速度和终端速度。Vm1和Vm2为待优化的参数,文后的论述中取Vm1=4800m/s ,Vm2=3000m/s[8]。
驻点热流密度、过载和动压约束分别取:

其中,Rd为飞行器头部曲率半径,c为与飞行器特性相关的常数。
忽略地球自转,令式(2)为0,近似认为cosγ=1,可得准平衡滑翔条件[4]

为了保证一定的再入飞行机动性能,取其中的倾侧角为一个固定值σEQ,得到准平衡滑翔约束为
准平衡滑翔约束式(12)将高度限制在一定范围内,可以降低滑翔轨迹在高度方向的振荡。本文取σEQ=5°。

再入轨迹生成是根据给定的初始状态,设计一条满足再入运动方程约束、攻角和倾侧角大小约束、再入走廊约束和终端约束的参数变化曲线。终端约束可描述为

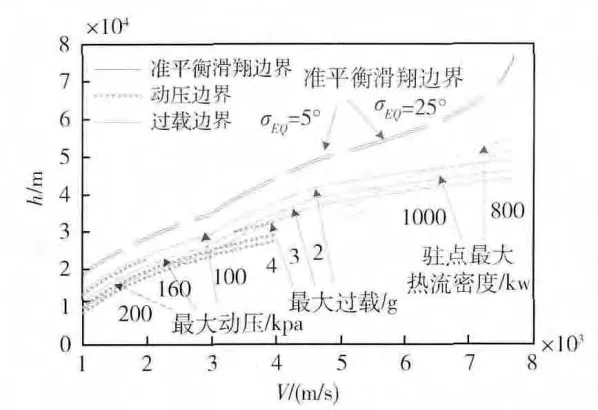
图1 再入走廊与飞行器参数的关系
2 纵向约束条件的转化
2.1 准平衡滑翔段制导约束的转化
由准平衡滑翔条件可知,如果CAV处于准平衡状态,那么V-h曲线只取决于倾侧角的大小|σ|。
将再入走廊的上下边界代入式(11),解算出倾侧角的范围,如图2所示。

图2 再入走廊约束转化成的倾侧角约束
将σ的上边界记为σmax,下边界记为σmin。如果再入轨迹处于准平衡滑翔状态,再入走廊约束式(8)~(12)可转化为如下倾侧角约束:

2.2 初始下降段制导约束的转化
将初始下降段(IDP)的倾侧角当作一个常值处理(记为σ0),因为攻角剖面已定,所以初始下降段的约束转化为寻找一个 σ0的可行范围[σ0min,σ0max],使得CAV能安全过渡到准平衡滑翔状态。
在QEGC下,对于给定的α文件和一个固定的σ0,由上节可知,r是V的函数r(V)。因此CAV经过初始下降段进入准平衡滑翔状态的条件为[4]


图3 倾侧角对初始下降段的影响
因此在初始下降段,当以固定倾侧角飞行时,会有一个最大初始倾侧角|σ0|max。当|σ0|≤|σ0|max时,可保证CAV的下降轨迹不超过热流密度极限,并且达到准平衡滑翔条件。为了克服再入轨迹在高度方向的振荡,一般|σ0|取小于但接近|σ0|max的值。
2.3 不确定因素对约束转化的影响
考虑攻角剖面、大气密度模型和气动模型误差影响,研究其变化对倾侧角范围的影响如图4所示。
仿真结论:负的攻角偏差、负的升力系数偏差或者正的阻力系数误差会使倾侧角的允许范围缩小(但是阻力系数误差的影响很小),以上3种因素的总和使得倾侧角的允许范围更小。
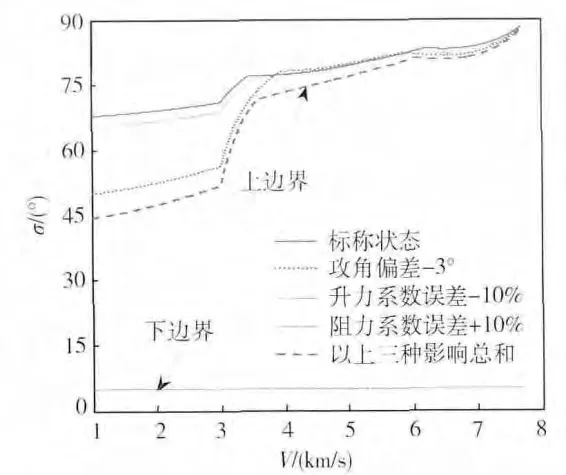
图4 不确定因素对约束转化的影响
3 三维轨迹在线生成
3.1 纵向轨迹在线生成
为实现在线轨迹规划,将控制变量|σ(V)|的无穷维规划问题转化为单参数搜索问题,设计|σ(V)|为如下分段线性函数(倾侧角特征参数)[4]

同时|σ(V)|还需满足式(14)的约束,其中,(σ1,V1)和(σ2,V2)分别为拟平衡滑翔段起点和终点的侧倾角和速度,Vmid=kvV1-V2)。本文取kv=0.6654,那么σmid为在线轨迹规划唯一的搜索参数。
3.2 横向机动轨迹设计
高超声速滑翔飞行器的横向机动突防弹道是其区别于其他再入飞行器的主要标志之一。本节将地面威胁考虑成禁飞圆约束,设计多约束条件下的滑翔式再入轨迹快速生成方法。在纵向弹道设计时已经给定了攻角α和倾侧角大小|σ|,横向机动突防弹道的设计主要是设计倾侧角的反转策略,以满足禁飞圆约束。考虑禁飞圆的横向制导几何关系如图5所示。

图5 横向制导几何关系
M是飞行器的当前位置,T是目标位置。MP是飞行器与禁飞圆O的切线,P为切点,Q是TQ与圆O的切点。其中相关几何关系计算式为:
1)视线角计算公式[7]:

由图5可知,当飞行器处于TQ和禁飞圆左边界(OQ左边的圆弧)的左侧时,飞行器与目标的视线MT要穿越禁飞圆;当飞行器在TQ禁飞圆右边界(OQ右边的圆弧)的右侧时,飞行器与目标的视线MT不被禁飞圆遮挡。因此将横向制导区域按TQ划分成2个区域:TQ左边且在禁飞圆左边的区域记为I区;TQ右边以及TQ与禁飞圆右边界的中间区域记为II区。
飞行器处于I区时,制导的任务是绕过禁飞区,又不能偏离目标点太远。
飞行器处于II区时(如图5所示的M'点),制导策略为速度方向朝向视线方向M'T。
基于以上推理,航向角误差走廊的数学表达式为:
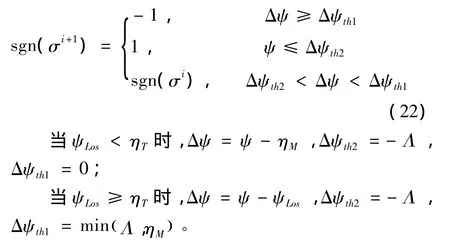

4 在线轨迹生成仿真
采用割线法可迭代出满足终端航程要求的σmid,记sf为终止时刻的剩余航程,迭代公式如下

当sf≤2°时,停止迭代。
4.1 仿真参数设置
参数配置如下
1)再入接口(EI)参数:
V0=7.200km/s,γ0=0rad,ψ0=1.3357rad,h0=120km,λ0=2.0595rad,φ0=0.5585rad。
2)终端约束:Vd=1800m/s,γd=1.1460°,Δψmax=8.5950°,sd=2°。
3)禁飞圆和目标区域参数:
目标位置 =(λT,φT)=(3.9270,0.0873)rad,
禁飞区圆心 =(λo,φo)=(π,0.4363)rad,禁飞圆半径RO=0.1745rad。
4)轨迹生成参数:初始值取σmid=0.4rad。
5)飞行器特性参数c=11030,Rd=1。
4.2 仿真结果和分析
仿真结果如图6~8所示。考虑禁飞区时,迭代了2次(积分3次再入运动方程),最终取σmid=0.42rad满足终端位置约束;不考虑禁飞区时,迭代1次(积分两次再入运动方程),最终取 σmid=0.48rad。
图6是生成轨迹的横向视图。在初始下降段,大气密度稀少,加上初始倾侧角较小,CAV的机动能力是有限的,所以在初始下降段,2条轨迹是重合的,在滑翔段才开始有区别。由图可以看出,本文的横向机动轨迹生成方法能够有效地避开地面威胁,终端位置达到了很高的精度。
图7是航迹角和航向角的变化情况。由图7(a)可知,本章仿真采用的航向角初始误差是很大的。在初始下降段,虽然将倾侧角符号调整为负,但没有足够的机动将航迹角调整在航向误差走廊内。能量值小于0.73时,CAV位于I区,CAV以其与禁飞圆上边界决定的切线为参考航迹飞行,此时航向走廊的上界也是此切线。当能量大于0.73时,CAV位于II区,CAV以目标视线为参考方向,航向走廊上界开始不等于参考航向角。在e∈(0.7,0.73)区间内,是CAV处于离禁飞圆边界最近的区域,此时CAV的参考方向剧烈变化,虽然倾侧角符号此时为正,航向角也没保持在航向走廊内。但这种情况也使得航向角不可能靠近航向走廊的上界,即CAV不可能进入禁飞圆内。图7(b)是考虑威胁和无视威胁2种情况下航迹角的变化情况。可以看出,除初始下降段外,2种情况下的再入轨迹处于准平衡滑翔状态。

图6 考虑威胁的横向突防轨迹
由图8(a)可以看出,倾侧角经历了5次符号跳变,这是图8(a)的航向角变化情况的更深入解释。图8(b)说明2种情况下的再入轨迹均有较小振荡,但都离再入走廊下边界刚性约束较远,这是因为图8(a)中的倾侧角离倾侧角边界较远。说明了在纵向和横向的耦合下,本文的再入走廊约束转化成倾侧角约束的方法是很有效的。
5 结论
首先分析了再入轨迹生成问题的基本要素和再入走廊的概念,接着利用准平衡滑翔条件分别将初始下降段和滑翔段的热流密度、过载及动压约束转化成了倾侧角约束,并分析了攻角剖面的改变、大气模型的误差、气动模型的误差对这种约束转换的关系。通过仿真得到结论:大气模型改变再入轨迹在h-V剖面的位置,但不改变倾侧角范围,攻角的负增量、升力系数的负误差、阻力系数的正误差会缩小倾侧角的允许范围。然后,分别设计了纵向的单参数航程搜索方法和横向考虑禁飞圆的机动轨迹生成算法。因为准平衡滑翔状态是再入走廊约束转化为倾侧角约束的基本前提,所以,在滑翔段轨迹生成过程中考虑了准平衡滑翔保持方法。横向机动轨迹生成算法主要利用了禁飞圆的切线以及目标视线角信息,数值仿真证明算法鲁棒性强、易于实施。

图7 航迹角和航向角-能量曲线
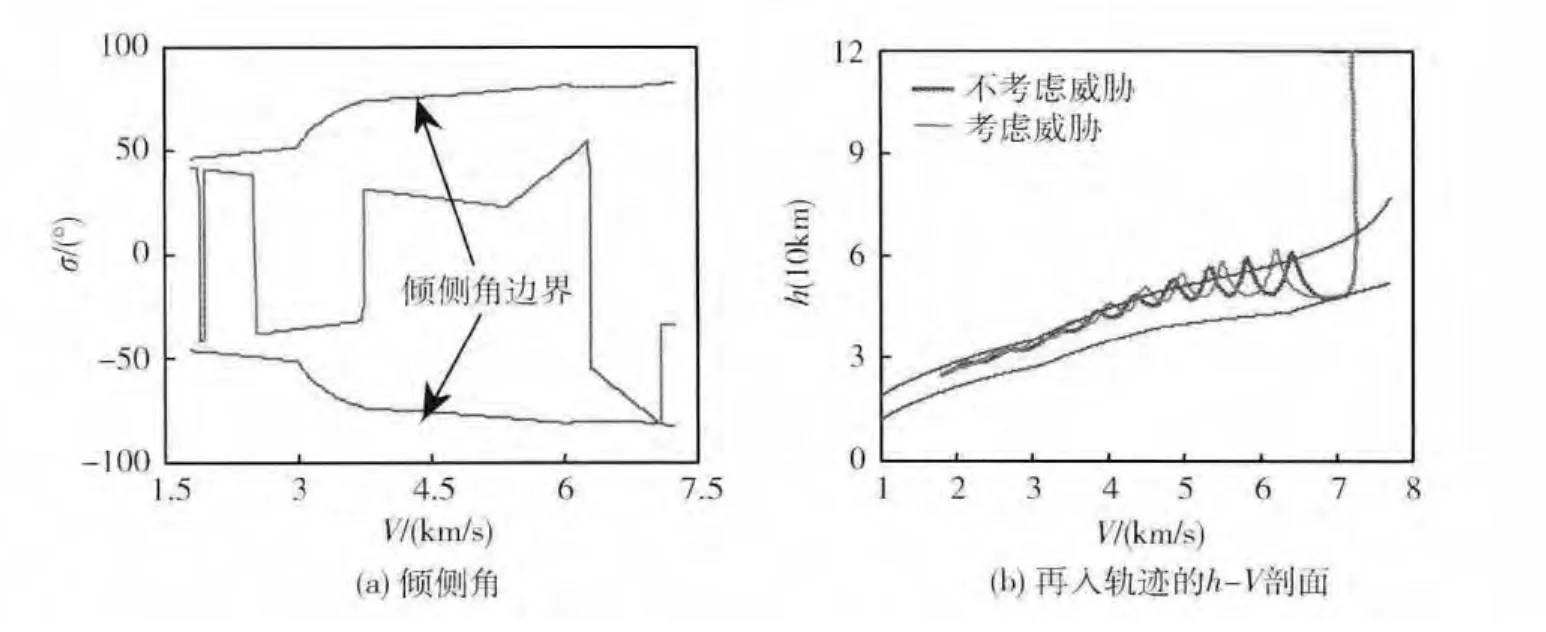
图8 倾侧角变化和再入轨迹的约束情况
[1] Jorris Timothy R.Common Aero Vehicle Autonomous Reentry Trajectory Optimization Satisfying Waypoint and No-fly Zone Constraints[D].Air University,2007.
[2] 雍恩米,唐国金,陈磊.高超声速无动力远程滑翔飞行器多约束条件下的轨迹快速生成[J].宇航学报,2008,29(1):46-52.(Yong E M,Tang G J,Chen L.Rapid trajectory planning for hypersonic unpowered longrange reentry vehicles with multi-constraints[J].Journal of Astronautics ,2008,29(1):46-52.)
[3] Jouhaud F.Closed loop reentry guidance law of a space plane:application to hermes[J].Acta Astronautic,1992,26(8-10):577-585.
[4] Shen Z J,Lu P.Onboard generation of three-dimensional constrained entry trajectories[J].Guidance Control Dynamics,2003,26:111–121.
[5] Ping Lu,Stephen Forbes,and Morgan Baldwin.gliding guidance of high L/D hypersonic vehicles[J].AIAA Guidance,Navigation,and Control(GNC)Conference August 19-22,2013,Boston,MA.
[6] Philips T H.A Common Aero Vehicle(CAV)Model,Description and Employment Guidance[R].Schafer Corporation,2003.
[7] 胡建学.可重复使用跨大气层飞行器再入制导研究[D].长沙:国防科学技术大学,2007.
[8] 朱凯,齐乃明.滑翔导弹再入制导与控制方法研究[D].哈尔滨:哈尔滨工业大学,2011.

