基于小样本数据的惯性平台系统贮存可靠度的预测方法

杨宝琨 康兴无

1.北京航天自动控制研究所，北京100854

2.第二炮兵工程大学，西安710025

惯性平台系统作为精确导航定位系统已广泛应用于航天、航空、航海等军用和民用设施中。应用于导弹装备的惯性平台系统在使用之前长期处于贮存状态［1-2］，通常情况下，由于系统受到环境因素和维修管理因素的影响，它们的可靠性将随时间的延长而降低，导致功能异常或精度降低。惯性平台系统的贮存可靠性是指惯性平台系统从出厂之日起，在规定的贮存环境和规定的贮存期内保持正常使用的概率，反映对贮存环境的固有适应能力［3］。在惯性平台系统的贮存期内经常对惯性平台系统进行寿命试验可以得到较为准确的贮存寿命，但是耗时长，费用大，通常难以实现。所以，一般采用定期检测的方式对惯性平台系统进行检测与维修［4］。因此，定检数据便成为评价惯性平台系统长期贮存可靠性的重要参考依据。如何通过这些定检数据来获得惯性平台系统的贮存可靠度，并预测其将来的可靠度是工程师和决策者主要关心的问题。

近年来，很多文献中对贮存过程中大型系统的可靠度和风险分析提出了多种研究方法［5-8］;基于定检数据的军事装备系统贮存可靠度也越来越受到重视［9-17］。事实上，惯性平台系统非常昂贵且寿命有限，其定期检测又受到多种因素的限制，不可能像一般产品那样对多个样本进行完整的测试，因此导致定检数据为小子样数据。传统的预测方法，例如多项式回归预测法和灰度预测法等都是基于大数定理对大样本数据进行分析的预测方法，所以，应用多项式回归预测法和灰度预测法进行小样本数据的贮存可靠度预测存在缺陷。

基于上述因素，支持向量机作为一种寻找复杂变量之间关系的新方法而被用来对惯性平台系统的贮存可靠性进行预测研究。它能得到模型和基于有限样本的学习能力之间最好的关系，还可以避免其他方法在预测过程中的过学习现象。最小二乘支持向量机(LSSVM)是Suykens［18］提出的一种新的支持向量机模型有许多优点:操作简单、快速收敛和高精度等。考虑到惯性平台系统定检数据的特点和LSSVM的优势，本文选用LSSVM对惯性平台系统的贮存可靠度进行预测分析，提出了一种基于专家经验的方法来预测基于定检数据的惯性平台系统贮存可靠度，引入最小二乘支持向量机方法预测贮存可靠度。由于研究惯性平台系统整体的贮存寿命非常困难，需要先对其各部件的贮存寿命进行计算并预测。文中针对惯性平台系统某部件性能参数展开分析，计算并预测其贮存可靠度。

1 贮存可靠度的基本概念

可靠性定义为:产品在规定条件下和规定时间内，完成规定功能的概率［19］。其主要指标为可靠度，贮存可靠度指的是产品在贮存期间内完成规定功能的概率，是一个统计学概念。

由可靠度的基本概念可知，要确定产品的贮存可靠度需要收集其统计数据，进行处理并建模计算。根据专家经验和调研发现［20-21］，文中使用的数据类型为正态分布，可以通过正态分布可靠度理论进行可靠度的计算。

2 定检数据的预处理

惯性平台系统历年的定检数据是评价惯性平台系统贮存可靠度的参考依据，在对其进行可靠度的计算和预测之前需要先进行预处理［22］，步骤如下文。

2.1 定检数据异常值的剔除

惯性平台系统在贮存期内的定期检测需要专门的测试设备和技术人员。由于设备和人员水平的原因，人工采集数据时，有时会发现某个数据与整体数据的变化规律相差很大，这个测试数据被称作异常数据。需找出产生异常数据的原因，分析其对结果的影响程度;或者采用相应的数据处理方法对其进行数据处理，以免对结果分析带来不合理的影响。

服从正态分布的测试数据，适合采用拉依达判据对其进行预处理，方法如下:

定检数据的总体服从正态分布，则

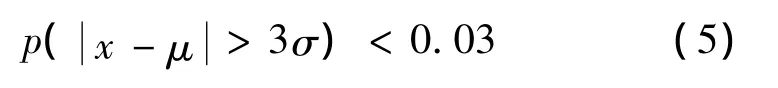
其中，μ和σ分别是正态分布的数学期望和标准偏差。若定检数据为 x1，x2，x3，…，xn，则

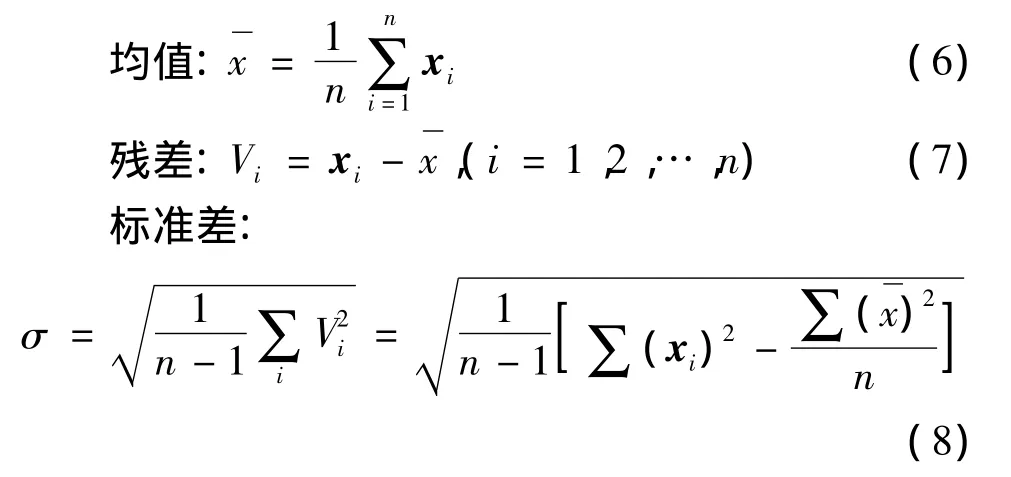
若某个定检数据xd的残差Vd(1＜d＜n)满足下式

则认为xd为异常值，予以剔除。

2.2 定检数据缺失值的替补

根据对定检数据的浏览和预处理，发现定检数据存在缺失现象，具体表现为:历年的数据集合中存在单一缺失;同批次的定检数据存在整年的缺失。所以，在进行贮存可靠度的计算和预测之前，还要完成定检数据缺失值的预处理。

许多实际工程问题中，有一些测试数据无法获得或者已经缺失。如果缺失比例相对很小，可直接舍弃缺失数据并进行后续分析;但在某些具体的测试数据中，缺失数据往往占有相当大的比重，尤其是多元数据，此时前述的数据处理方法不再合适，需要采取其他方法(例如均值法［20］)对其进行数据替补来保证数据整体的完整性和一致性。

文中以第8年的性能参数数据为例，采用缺失数据相邻最近两元素的均值来替换缺失数据的办法对定检数据进行替补。

2.3 定检数据的分布拟合

定检数据经过上述2个步骤的预处理后，根据可靠度计算的要求还需要确定它的分布类型，通过数据的分布类型来确定计算可靠度的方法。定检数据反映的是产品性能状态的指标参数，其具体的数据分布类型很难确定。根据以往的专家经验和研究文献［20-21］发现，其分布规律近似服从正态分布或者威布尔分布。因此要对预处理过的定检数据进行分布规律的拟合分析，并最终确定其分布类型。

采用传统的解析法对预处理数据进行精确的分布类型检验难以实现，本文采用专业数据统计软件进行分布拟合检验。以X，Y方向漂移系数K 1，K 2为例，图1为采用专业统计分析软件SPSS对K 1参数进行正态分布的检验图。可以看出，K 1参数数据的拟合曲线与理想正态分布曲线非常接近，可确定K 1参数符合正态分布;通过同样的方法，得到K 2参数也是符合正态分布的。

图1 K 1的正态分布检验

3 基于支持向量机的贮存可靠度预测

可靠度预测方法多采用多项式回归预测、灰度预测等传统方法。本文根据定检数据小样本的特点，采用当前较为流行的支持向量机预测法来进行贮存可靠度的预测。

支持向量机采用结构最小化准则，在最小化样本误差的同时，能缩小模型泛化误差的上界，使得模型的结构风险最小化，具有任意逼近非线性映射的能力，在小样本学习中表现得尤为突出。

考虑到贮存期间内样本数据只有11个，应该对样本数据进行数据重构来扩充数据信息，获得较为准确合理的预测模型;另外一个目的是选择最好的超参数来优化LSSVM的泛化能力。

假设训练集为 {xi，yi}L-mi=1，xi，yi∈ Rn如下所示:

r(i)是每年的可靠度值，xi是输入值，yi是预测值，L，m分别是初始序列长度和嵌入维数。通过引入嵌入维数，实测中的定检数据得到了扩充与重构，能够更好的反映数据间的关联关系，尽可能的挖掘定检数据的信息量，提高预测模型的精度。

贮存可靠度的预测优化问题可以表示为:

4 举例

根据上述方法对11年贮存期内的惯性平台系统定检数据分析计算，得到了其可靠度，并使用多种方法进行预测，结果如下:图2和3为贮存期11年内某性能参数K 1和K 2的贮存可靠度值。由图2可以看出，K 1的可靠度在整个11年的贮存期内上下波动，有明显的下降趋势。图3表明，K 2的可靠度在整个贮存期内存在上下波动，但整体趋势是上升的。分析其上升的原因:1)产品在设计时存在可靠性增长环节;2)产品在贮存期内，其失效部件被及时维修和更换。根据调研发现，导致惯性平台系统贮存可靠度上升的主要原因是第2个因素。

图2 K 1的贮存可靠度计算值和预测值

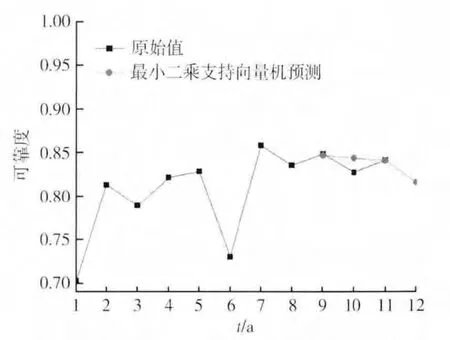
图3 K 2的贮存可靠度计算值和预测值

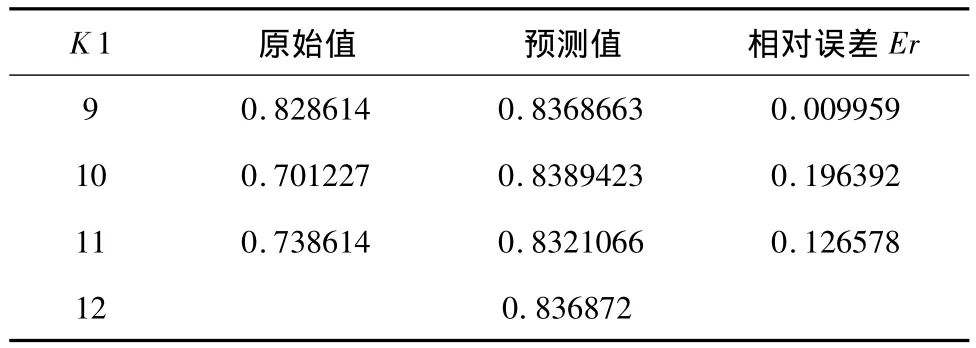
表1 K 1贮存可靠度预测误差

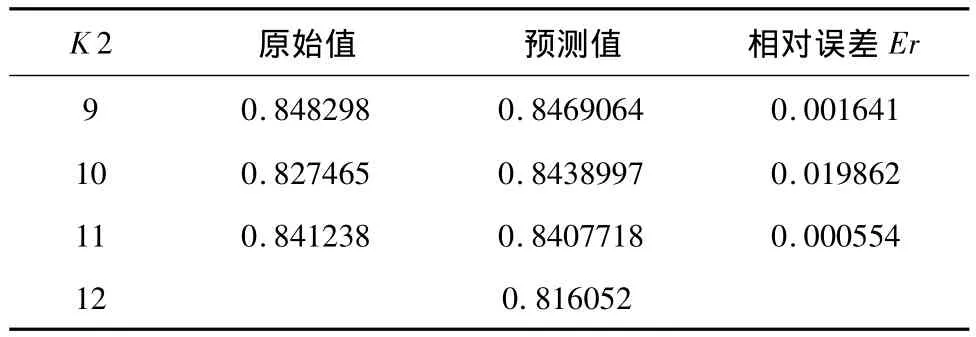
表2 K 2贮存可靠度预测误差

传统的预测方法有多项式回归预测、灰度预测等。下面将上述2种预测方法的预测结果与支持向量机方法的预测结果比较，如图4和5所示。

综合图4和5可以看出，多项式回归预测法虽然在前11年的可靠度值吻合的很好，但第12年的预测值误差很大，说明多项式回归预测方法处理小样本数据时，存在过学习的现象;灰度预测法的预测效果相比多项式回归预测较好，趋势一致，但由于灰度预测方法对小样本数据的前6阶较为依赖，缺少了预测的随机性，最终导致误差偏大。通过以上对比发现使用支持向量机预测法得到的预测结果较为合理，准确。

图4 K 1贮存可靠度预测比较

图5 K 2贮存可靠度预测比较

5 结论

通过分析惯性平台系统的定检数据，建立了其贮存可靠度的计算模型。使用最小二乘支持向量机预测法、多项式回归预测法和灰度预测法分别对惯性平台系统的贮存可靠度进行预测。结果表明，针对惯性平台系统贮存定检数据小样本的问题，最小二乘支持向量机预测法的预测效果较为理想。研究结果可以为惯性平台系统的贮存延寿研究提供技术支持，为惯性平台系统的可靠性设计、确定预防性和维护性要求提供参考。

［1］ Smith H B，Rhodes C A.Storage reliability prediction handbook for parts count prediction［R］.USA:Raytheon Co.，Life Cycle Analysis Group.Octember，1982.

［2］ Menke J T.Deterioration of electronics in storage［J］.National SAMPE Symposium，1983，28:966-972.

［3］ 陈万创.防空导弹可靠性指标与验证方法探讨［J］.上海航天，2002，19(3):6-9.(Chen Wanchuang.Discussion on reliability index and verification method［J］.Aerospace Shanghai，2002，19(3):6-9.)

［4］ 周堃，罗天元，张伦武.弹箭贮存寿命预测预报技术综述［J］.装备环境工程，2005，2(2):6-11.(Zhou Kun，Luo Tianyuan，Zhang Lunwu.Prediction techniques for storage life for missiles［J］.Equipment Environmental Engineering，2005，2(2):6-11.)

［5］ 罗吉庭，罗强.串联系统可靠性评估方法的综合述评［J］.宇航学报，1996，17(2):36-39.

［6］ 荣吉利，张涛，徐天富，等.性能参数型航天器机构的可靠性试验评定方法［J］.宇航学报，2012，33(3):387-391.(Rong Jili，Zhang Tao，Xu Tianfu，et al.Study on test method of reliability assessment used for performance parameter measured spacecraft mechanism［J］.Journal of Astronautics，2012，33(3):387-391.)

［7］ 唐樟春，吕震宙，吕媛波.一种与样本信息合理匹配的可靠性模型［J］.宇航学报，2010，31(3):895-901.(Tang Zhangchun，Lv Zhenzhou，Lv Yuanbo.A novel reliability model matching information involved in sample data［J］.Journal of Astronautics，2010，31(3):895-901.)

［8］ 李学京，杨军.基于可靠性增长试验信息的可靠性综合验证方法［J］.宇航学报，2008，29(3):1074-1079.(Li Xuejing，Yang Jun.Reliability integrated compliance test based on reliability growth inforamtion［J］.JournalofAstronautics， 2008，29(3):1074-1079.)

［9］ 孙亮，徐廷学，代莹.基于定期检测的导弹贮存可靠性预测模型［J］.战术导弹技术，2004(4):16-19.(Sun Liang，Xu Tingxue，Dai Ying.Models of storage reliability prediction based on periodical test for missiles［J］.Tactical Missile Technology，2004，(4):16-19.)

［10］ 周苏明.由定检数据评定指数寿命型部件贮存可靠性［J］.电子产品可靠性与环境试验，1995，(6):2-7.

［11］ 徐军辉，汪立新，钱培贤.延长捷联惯组稳定期的方法研究［J］.宇航学报，2007，28(6):1560-1564.(Xu Junhun，Wang Lixin，Qian Peixian.The method study of increase the stabilization period of SIMU［J］.Journal of Astronautics，2007，28(6):1560-1564.)

［12］ 陈迪，周百里，费鹤良.导弹系统贮存可靠性预测的数学模型［J］.宇航学报，1996，17(3):68-75.

［13］ 李正，童小燕，吕胜利.小子样装备贮存可靠性评定方法［J］.机械设计与制造，2006(12):74-76.(Li Zheng，Tong Xiaoyan，Lv Shengli.The storage reliability assessment for small-sample equipment［J］.Machinery Design＆ Manufacture，2006(12):74-76.)

［14］ 刘春和，陆祖建，袁玉华.导弹贮存可靠性评估［J］.数学的实践与认识，2001，31(4):414-420.(Liu Chunhe，Lu Zujian，Yuan Yuhua.The storage reliability assessment for missile［J］.Mathmatics in Practice and Theory，2001，31(4):414-420.)

［15］ 单鑫，董文洪，曹阳.导弹设备贮存可靠性灰色预计模型［J］.弹箭与制导学报，2007，27(1):308-310.(Shan Xin，Dong Wenhong，Cao Yang.Storage reliability grey prediction model for missile equipment［J］.Danjian Yu Zhidao Xuebao，2007，27(1):308-310.)

［16］ 吴进煌，戴邵武，徐胜红.基于可靠度预测模型的导弹贮存寿命分析方法［J］.海军航空工程学院学报，2005，20(4):477-479.(Wu Jinhuang，Dai Shaowu，Xu Shenghong.Analysis method of missile storage life based on forecasting model of storage reliability［J］.Journal of Naval Aeronautical Engineering Institute，2005，20(4):477-479.)

［17］ 王军波.装备贮存可靠性指标的统计描述［J］.军械工程学院学报，1995，7(3):58-63.(Wang Junbo.Statistical description for equipment storage reliability［J］.Journal of Ordnance Engineering College，1995，7(3):58-63.)

［18］ J A K Suykens，J Vandewalle，B De Moor.Optimal control by least square support vector machines［J］.Neural Networks，2001，14(1):23-25.

［19］ 金星，洪延姬.系统可靠性与可用性分析方法［M］.北京:国防工业出版社，2007.

［20］ 梅硕基.惯性仪器测试与数据分析［M］.西安:西北工业大学出版社，1991.

［21］ 徐国平.基于支持向量机的动调陀螺仪寿命预测方法研究［D］.上海:上海交通大学，2008.(Xu Guoping.Research on life forcasting methods of a DTG based on support vector machine［D］.Shanghai，Shanghai Jiao Tong University，2008.)

［22］ 阮金元，阮新.产品贮存可靠性数据收集和处理方法及贮存失效率预测模型的建模方法研究［J］.标准化报道，2000，21(1):7-11.(Ruan Jinyuan，Ruan Xin.Study on the methods for collection and process of storage reliability and setting up of forecasting model of storage failure［J］.Reporting of Standardization，2000，21(1):7-11.)

［23］ Kennedy J，Eberhart R.Particle swarm optimization［C］.Proceedings of The IEEE International Conference On Neural Networks，Perth，Australia，Nov 27-Dec 1，1995.

［24］ Vapnik V.The nature of statistical learning theory.［M］.Springer，New York，1995.