分散型多输入多输出雷达检测器设计及检测性能分析
李金梁 高 磊 曾勇虎 谢 虹
(电子信息系统复杂电磁环境效应国家重点实验室,河南 洛阳471003)
引 言
多输入多输出(Multiple-Input-Multiple-Output,MIMO)雷达是近年来获得广泛关注的一种雷达新概念[1-2].Fishler等[3]提出了分散型MIMO雷达的概念.分散型MIMO雷达各阵元之间的间距相对较大,利用空间分集改善雷达的检测性能,克服目标慢起伏引起的雷达检测性能下降[3-4].
分散型MIMO雷达基于空间分集在一次照射时间内得到目标回波的M×N个独立观测.对普通的单基地雷达,若在波束驻留时间内连续发射M×N个脉冲,当目标的回波起伏类型为快起伏时,也可以获得M×N个独立观测.虽然很多学者对分散型MIMO雷达的检测性能进行了研究[5-7],但都未涉及以上两种情况下检测性能的对比分析.且在以前的研究中,给出的最佳检测器一般结构复杂,难以工程实现.
实际上,经典文献[8-10]给出了相参积累和非相参积累等工程中广泛使用的检测器,并对多个脉冲相参或非相参积累后快起伏、慢起伏类目标的检测性能进行了分析,同时给出了检测性能的理论公式、经验公式和图表等.
基于此,本文首先对MIMO雷达和普通单基地雷达的回波信号模型进行分析,指出了MIMO雷达回波和单基地雷达快起伏目标多脉冲回波之间的相似关系.然后借鉴单基地雷达快起伏目标非相参积累的检测器结构,提出MIMO雷达也可以采用类似的包络检波级联累加器的检测器结构形式.包络检波分为线性和平方律两种.最后,就平方律包络检波级联累加器的检测器结构,对不同空域起伏目标的检测性能进行了推导,给出了检测性能的理论和仿真曲线.
1 回波信号模型等效
1.1 MIMO雷达回波信号模型
假设MIMO雷达发射机数目为M,接收机数目为N,发射信号的总能量为E,根据文献[3],MIMO雷达的回波信号模型为
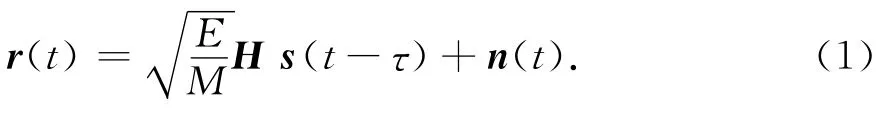
式中:r(t)=[r1(t),r2(t),…,rN(t)]T,rn(t)为第n个接收机接收到的回波信号;H为信道矩阵,

Anm=αnm,αnm为第m个发射机和第n个接收机组合下目标的散射复幅度,a(x0,y0)=[1,ejφ2,…,ejφM]T为发射机导向矢量,是一个M×1的矢量,b(x0,y0)=[1,ejψ2,…,ejψN]T为接收机导向矢量,是N×1的矢量;n(t)=[n1(t),…,nN(t)]T为接收机噪声,假设接收机噪声服从白的零均值复高斯随机过程,协方差矩阵为IN,IN是N×N的单位矩阵;s(t)=[s1(t),s2(t),…,sM(t)]T,sm(t)为 第m个发射站的发射信号.
对每个通道接收的回波,利用M个发射信号分别进行匹配滤波,考虑到不同发射信号之间的正交性,则滤波后的输出为

假设发射信号的零延迟自相关最大,且对于每一个发射信号都满足单位能量约束,即

在目标回波时延τ处,回波的采样值为
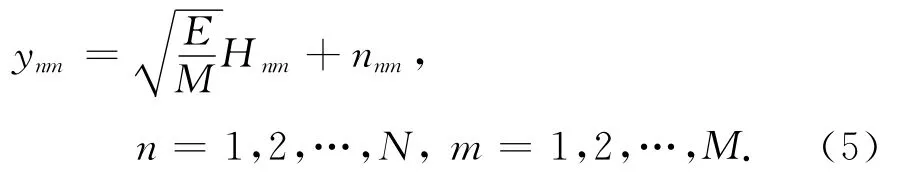
1.2 单基地雷达回波信号模型
对普通的单基地雷达,若在波束驻留时间内连续发射了N′个脉冲,假定雷达的发射信号为s(t),则目标的回波信号可以表示为

式中:τ=2R/c,R为目标的距离,假定目标在波束驻留时间内距离保持不变,c为光速;Ak为第k个脉冲时目标的回波幅度.
对雷达回波进行匹配滤波,并在目标所在位置进行采样,可得目标位置处匹配滤波的输出为
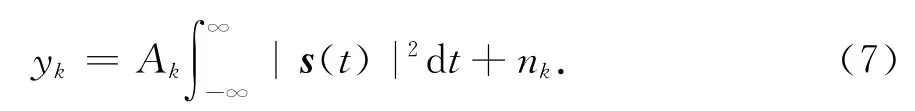
假定发射信号都满足单位能量约束,则式(7)变为
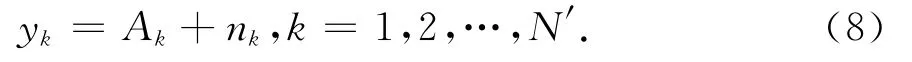
式(8)和式(5)相比,令
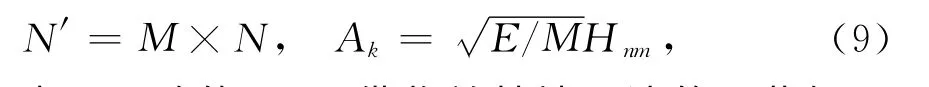
则二者是一致的.可以借鉴单基地雷达的一些知识来指导MIMO雷达的检测器设计.分析Ak和Hnm的影响因素及其变化规律.
1.3 空域起伏向时域起伏等效
对单基地雷达,不同脉冲对应的回波幅度Ak在时域会有一定起伏,起伏的原因主要归结于脉冲间目标上散射点之间的相对相位变化.散射点之间的相对相位变化主要有两方面的成因:一是目标的姿态变化,二是雷达工作频率的变化.根据雷达目标回波起伏时间相对于脉冲重复周期以及波束驻留时间的大小,Swerling等人将目标的时域起伏类型归纳为4类:第一类和第三类为脉冲间相关,扫描间独立,称之为慢起伏目标;第二类和第四类为脉冲间独立,称之为快起伏目标.第一类和第三类虽然同为慢起伏,但是由于雷达散射截面积(Radar Cross-Section,RCS)的概率分布函数不同,所以对应的检测性能也有所不同,对第二类和第四类目标,RCS服从类似的概率分布,只不过起伏较快.
对分散型MIMO雷达,不同方向得到的目标强度主要取决于信道矩阵.根据式(2),信道矩阵中元素的差异成因主要包括3部分:一是不同发射站到目标上各散射点之间的相位变化,二是目标在不同入射角和散射角的双站散射特性变化,三是目标上各点到不同接收站之间的相位差异.对分散型MIMO雷达目标回波强度起伏,可建模成和单基地雷达类似的概率分布形式.需要注意的是,对分布式MIMO雷达,布站时各站址相距较远,目标不同通道内幅度Hnm的分布相互独立[3],即MIMO雷达差异成因的第一部分和第三部分导致了不同通道内回波相互独立.
因此,若利用式(9)将MIMO雷达的回波信号模型式(5)等效为单基地雷达的回波信号模型式(8)时,需要明确两点:
1)Ak的相关性,是完全相关还是相互独立.如前所述,由于Hnm彼此相互独立,所以得到的Ak是相互独立的,即等效到时间起伏特性上时,等效为在时域脉冲间快起伏的目标.
2)Ak的概率密度函数P(Ak),即使P(Ak)=P(Hnm).对不同组成的目标,其空域起伏特性不同:
①若目标的组成为多个小散射体的组合(“多小组合”),则等效后Ak服从瑞利分布,对应的等效时域起伏类型为Swerling II型;
②若目标的组成为一个大的稳定散射体加多个小散射体(“一大加多小”)的话,则Ak服从莱斯分布,对应的等效时域起伏类型为Swerling IV型.
2 MIMO雷达检测器结构设计
根据上述等效的观点,MIMO雷达的检测问题可等效为单基地雷达对快起伏目标的多脉冲目标检测问题,因此可参照单基地雷达的现有常见检测器进行MIMO雷达检测器结构设计.对于快起伏目标,由于脉冲间目标回波的相位不相关,所以进行积累时,只能采用非相干积累,积累后进行检测.
非相干积累器一般是首先进行包络检波,去除随机相位的影响,然后再进行积累,即采用的的是包络检波级联累加器的检测器结构,如图1所示.
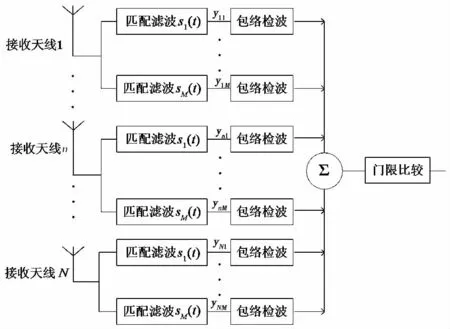
图1 MIMO雷达检测器形式
常见的包络检波器包括平方律检波和线性检波两种.采用平方律包络检波时,MIMO雷达目标检测的判决表达式为
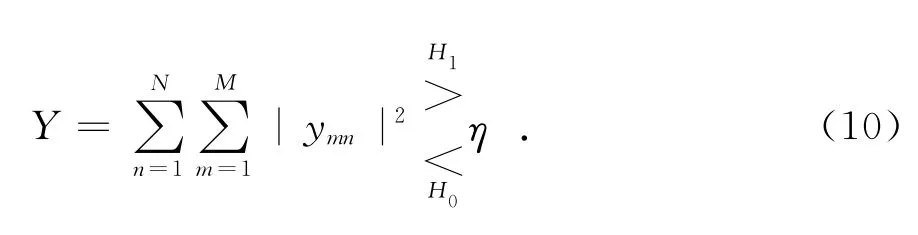
式中:η为检测门限;H1代表有目标;H0代表无目标.采用线性包络检波器时,MIMO雷达目标检测的判决表达式为

根据文献[3],式(10)为对应于“多小组合”目标的最佳检测器,文献[5]给出了“一大加多小目标”的最佳检测器,文献[6]给出了Rician分布目标的最佳检测器,不同分布类型的目标对应的最佳检测器的形式不同.有些形式的最佳检测器不便于工程实现,并且雷达检测器的结构往往是固定的,一般工作过程中难以得到目标起伏类型的先验信息,所以通常采用的应是一种易于工程实现的准最佳检测器.式(10)和式(11)所示的检测器对很多类型的目标并非最优,但工程实现较为简单.所以,我们提出,MIMO雷达可以采用式(10)或式(11)所示的检测器结构.
对不起伏和Swerling类型的目标,式(10)和式(11)所示的检测器性能相差不大,式(10)所示的检测器可以得到虚警概率和检测门限之间的解析表达式,更利于分析,所以本文主要分析该检测器对各类目标的检测性能.
3 雷达检测性能分析
3.1 对“多小组合”目标检测性能的分析
将MIMO雷达M×N个通道内的目标回波等效为单个发射天线和接收天线连续发射M×N个脉冲的情况,根据文献[10],可基于特征函数分析多个脉冲积累时的雷达检测性能,变量和的特征函数等于多个变量特征函数的乘积.“多小组合”时,回波服从指数分布其特征函数为
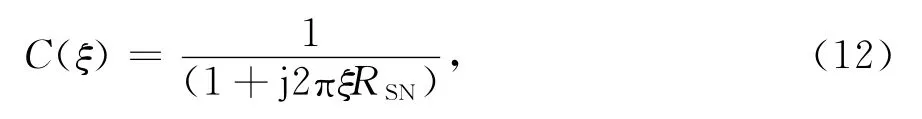
RSN=E/(为等效后单个脉冲回波信噪比.噪声的特征函数对应式(12)中RSN=1的情况.快起伏时,信号加噪声的M×N个样本和的特征函数可以通过将M×N个信号和噪声的特征函数相乘得到,即
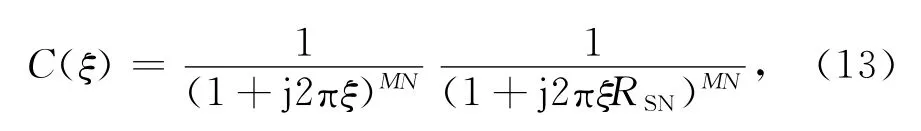
对特征函数进行逆傅里叶变换得到其概率密度函数
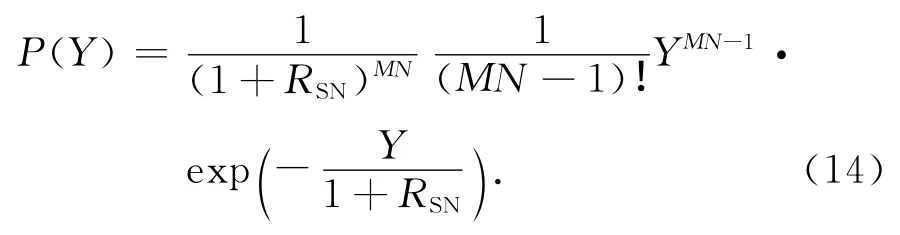
无目标时,RSN=0,式(14)可以表示为
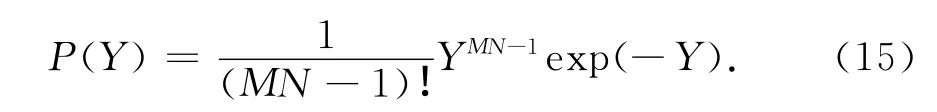
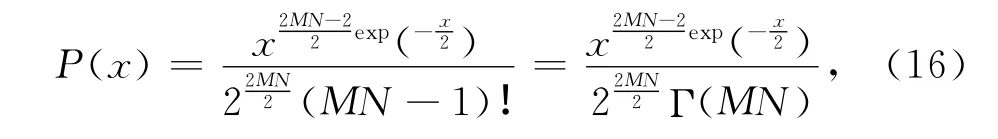
Γ(·)为Gamma函数,Γ(N)=N!.从式(16)可以看出,x服从自由度为2 M×N的χ2分布.可以得到

虚警概率Pfa与检测门限η的关系为

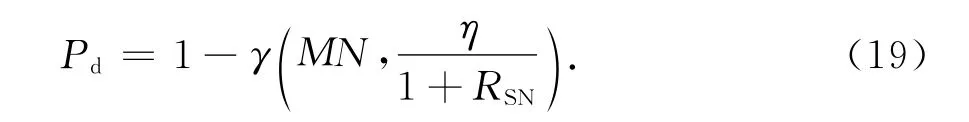
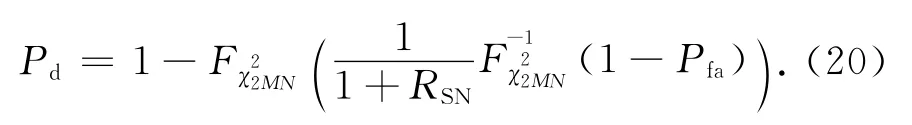
式(20)与文献[3]中式(29)相一致.
虚警率为Pfa=10-6,单个脉冲MIMO雷达检测概率Pd随单个通道信噪比RSN的变化曲线如图2所示.
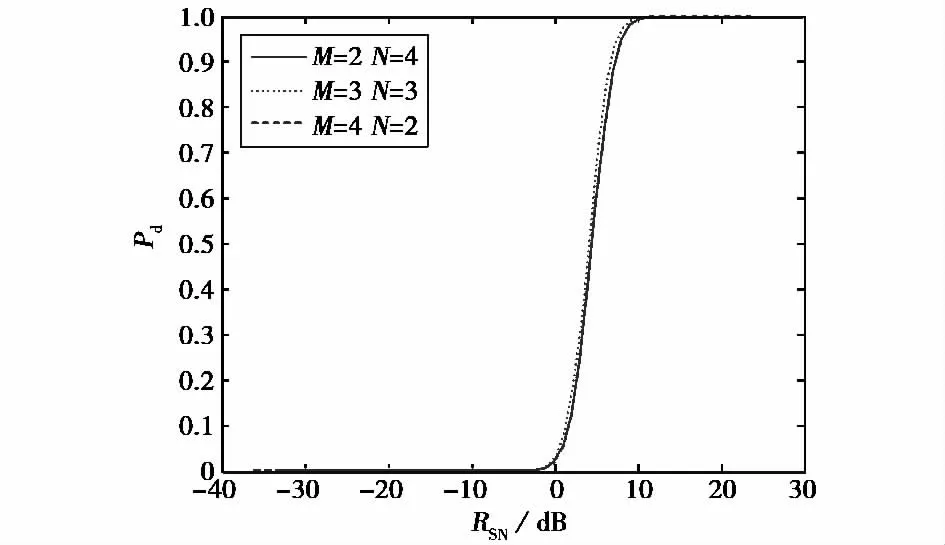
图2 MIMO雷达对“多小组合”目标检测性能曲线
从图2可以看出,M=2,N=4和M=4,N=2两种情况下的检测性能曲线是重合的,二者的检测性能略低于M=3,N=3时的结果.这是因为当RSN当相同时,MIMO雷达的检测性能只取决于乘积M×N.也就是说当单个阵元的发射能量一定时,应该尽量增大M×N的取值.
但是如果发射信号的总能量E一定时,发射阵元数目M的增加会导致每个发射阵元发射能量的降低,进而RSN变小,从而带来检测性能降低.所以要提高检测性能,必须在减小发射阵元数目M和增大通道数M×N之间进行折衷.
3.2 对“一大加多小”目标和固定目标检测性能的分析
对“一大加多小”目标和固定目标的检测性能难以得到解析表达式,采用仿真的方法进行检测性能分析.图3为M=2,N=4时,式(10)所示的MIMO雷达检测器对不起伏目标、“多小组合”(v=2)和“一大加多小”(v=4)型目标的检测性能仿真结果.
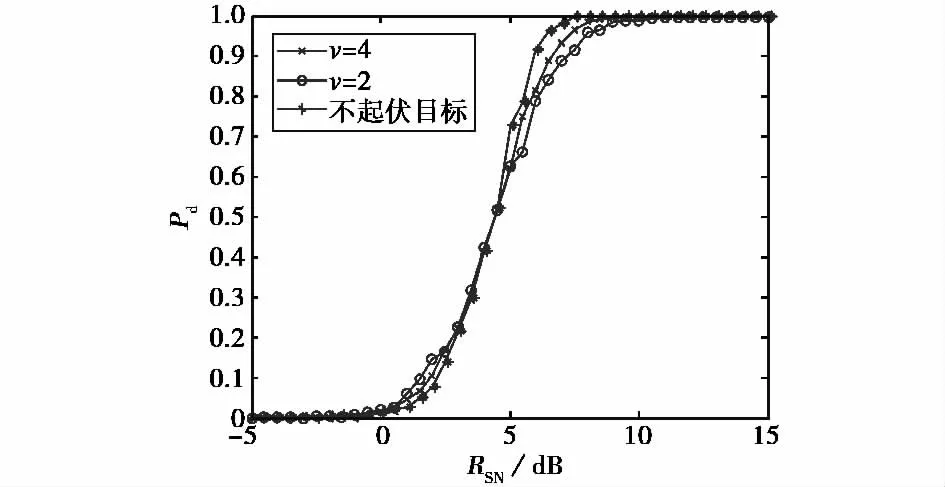
图3 MIMO雷达对不同类型目标检测性能仿真结果
从图3可以看出,相比于固定目标,在高信噪比区域,“多小组合”(v=2)和“一大加多小”(v=4)的检测概率有一定程度的下降,即存在一定的起伏损耗.同时可以看出,在高信噪比区“一大加多小”目标的检测性能略优于“多小组合”目标,介于“多小组合”目标型和固定目标之间.
4 结 论
论文基于等效的方法对MIMO雷达检测器结构进行了设计,将MIMO雷达M×N个通道等效为单基地雷达的M×N个脉冲,并对等效后的目标起伏特性进行了分析.在此基础上,提出了包络检波级联累加器的MIMO雷达检测器结构,并就所提检测器的性能进行了分析和仿真.论文还只是分析了MIMO雷达基于单个脉冲回波进行检测的情况,对多个脉冲的情况有待下一步开展.
[1]FISHLER E,HAIMOVICH A,BLUM R,et al.MIMO radar:an idea whose time has come[C]//IEEE Radar Conf.Philadelphia,2004:71-78.
[2]马晓峰,汤永浩,盛卫星.多输入多输出雷达发射天线低旁瓣设计[J].电波科学学报,2012,27(6):1198-1203.MA Xiaofeng,TANG Yonghao,SHENG Weixing.Low sidelobe transmit antenna design for MIMO radar[J].Chinese Journal of Radio Science,2012,27(6):1198-1203(in Chinese)
[3]FISHLER E,BLUM R S,CIMINI L J,et al.Spatial diversity in radars——models and detection performance[J].IEEE Trans on Signal Processing,2006,54(3):823-838.
[4]HAIMOVICH A M,BLUM R S,CIMINI L J,et al.MIMO radar with widely separated antennas:reviewing recent work[J].IEEE Signal Processing Magazine,2008,25(1):116-129.
[5]TUAMAS A,VISA K.Performance of MIMO radar with angular diversity under swerling scattering models[J].IEEE Journal of Selected Topics in Signal Processing,2010,4(1):101-114.
[6]汤 俊,伍 勇,彭应宁,等.MIMO雷达对空域Rician起伏目标检测性能研究[J].中国科学F辑:信息科学,2009,39(8):866-874.TANG Jun,WU Yong,PENG Yingning,et al.Research on spatial rician fluctuation target detection performance of MIMO radar[J].Chinese Science Volume F:Informance science,2009,39(8):866-874(in chinese)
[7]张海成,杨江平,王晗中.具有未知参数的多输入多输出雷达弱目标检测[J].电波科学学报,2012,27(1):106-109.ZHANG Haicheng,YANG Jiangping,WANG Hanzhong.The performance of weak target detection with unknown statistic on MIMO radar[J].Chinese Journal of Radio Science,2012,27(1):106-109(in chinese)
[8]王小谟,匡永胜,陈忠先,等.监视雷达技术[M].北京:电子工业出版社,2008.
[9]BARTON D K.南京电子技术研究所,译.雷达系统分析与建模[M].北京:电子工业出版社,2007.
[10]MEILKE H D.Modern Radar System[M].Press Artech House,2008.

