系统矩阵表示的电磁场时域计算方法
郑宏兴 张玉贤
(天津职业技术师范大学 天线与微波技术研究所,天津300222)
引 言
麦克斯韦电磁学理论体系的建立,对现代文明产生了重大影响.伴随计算机技术的快速发展,人们采用有限元法[1-2]、矩量法[3-4]和时域有限差分(Finite Difference Time Domain,FDTD)法[5-6]等数值计算方法,通过编程来求解麦克斯韦方程组,模拟空间中的电磁场分布,从而解决复杂结构的电磁学工程应用问题,目前已经广泛应用于微波与毫米波通信、雷达、导航和地质探测等各个领域.FDTD是在时域内直接求解麦克斯韦方程组,标志性的工作是Yee提出的立方体网格剖分[5],电场和磁场分开半个时间步交错迭代,优点是计算的物理过程直观,对复杂目标建模相对容易,在计算机内部存储变量按照时间递推过程进行更新,对计算机内存要求相对较低,但是时间步长和空间网格受到稳定性条件的限制[6].后 来,Namiki[7]和Zheng[8]分 别 提 出了无条件稳定技术,从而突破了时间离散间隔的限制,采用变换方向的隐式(Alternative Direction Implicit,ADI)方法来求解方程,可实现无条件稳定.为了动态表达上述数值计算结果,一方面需要应用计算机的图形显示功能直观显示,另一方面还需要应用数字信号处理(Digital Signal Processing,DSP)[9-12]技术表达电磁波与物质的相互作用过程.DSP也是一门伴随计算机技术发展的数值计算技术,在语音、图像、地质探测和生物医学等方面得到广泛应用.无论是把DSP与计算电磁学相结合,用来处理等离子体或色散媒质的时间移位算子问题[9-10],还是将N阶色散媒质的研究与DSP技术相结合求解复杂结构问题[11],或者用系统函数来研究时域电磁问题等[12],这些都说明了两种方法相结合对电磁场数值计算的深入研究是很有意义的.
为了充分利用DSP技术的研究成果,本文按照信号与系统理论的概念,把电磁场的求解区域看做一个线性系统,讨论关于这个系统方程的建立过程.将电磁场方程的时域离散差分方程[13-14]转换为系统矩阵方程,通过分析时域迭代过程,将其纳入系统仿真问题[13-15]的框架下,结合DSP方法来实现将多维空间的多变量运算转换为一维矢量的运算,进一步给出在无条件稳定下电磁场方程所对应的系统矩阵的表示形式.利用系统矩阵求解麦克斯韦方程组,对时域和空域的电磁环境进行模拟仿真研究,达到分析电磁场问题、提高计算效率的目的.
1 电磁场方程的时域离散矩阵形式
考虑媒质的一般特性,有源区域中的麦克斯韦方程组可以表达为如下的对称形式[16]:

式中:Je=σe·E,Jm=σm·H分别为电流源和等效磁流源,σe和σm分别为电导率和等效磁损耗张量.以先计算磁场H,后计算电场E为主要计算过程,故设磁场H的时间步在n+1/2,电场E的时间步在n+1,如此实现式(1)和(2)的时域离散差分格式,得到:
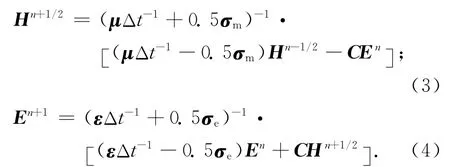
式中,C为旋度算子▽×的矩阵形式,定义为
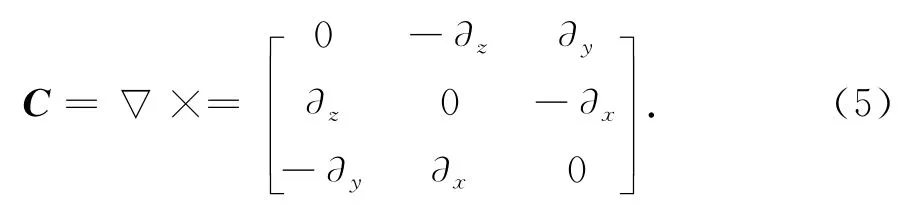
它是一个反对称张量.式(3)和(4)为麦克斯韦方程组的时域离散矩阵形式,按照时间递推,我们可以得到空间上波的传播过程.
2 时域差分方法的系统方程推导
由式(3)和(4),容易得到时域离散的电磁计算过程所对应的系统框图,如图1所示.

图1 传统FDTD计算过程的系统框图
显然,时域离散的电磁计算方法是利用时间上的交错迭代性质来模拟整个空间上的电磁场分布,并以此来描述空间中的电磁波传播过程.从式(4)发现,En+1中存在由Hn+1/2决定的场分量.将式(4)展开,

将式(3)中的磁场分量H移动1/2个时间步,得
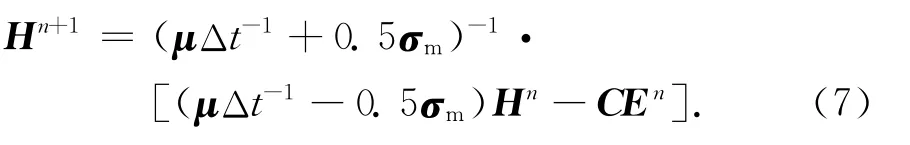
设x[n]={[E H]n}T是由电场E和磁场H在n时刻所有空间离散后的各点场量.如果把求解区域看做线性系统,那么式(6)和(7)描述的系统在n+1时刻的电磁场分布x[n+1],可以由图2所示的系统框图表达,图中R描述的是线性系统的系统矩阵,定义为

图2 关于系统矩阵R的电磁场迭代原理图
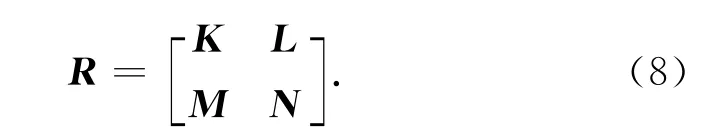
由式(6)和(7)分别得到:
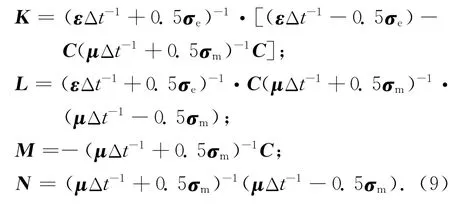
由系统矩阵R中的第一项子矩阵K可见,重复对电场E进行了两次空间微分运算,C矩阵的元素为空域上一阶导数,作用两次后使得电场E在空域上进行了二阶求导.从这里开始,在式(3)和(4)中所考虑的是多变量的交替问题,均可归结到数字信号处理的问题,其优势在于多变量的问题直接转换为一维矢量的问题,重点在于系统矩阵R中的元素分布情况.考虑到差分方程的求解过程中,这种电磁计算的系统方程应满足:
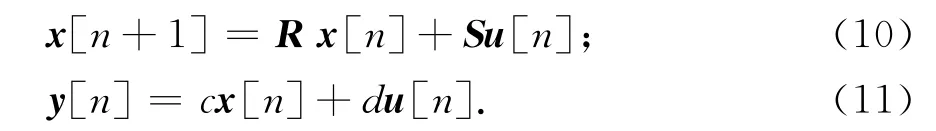
式中:S为激励源分布矩阵;u[n]为输入的激励信号;y[n]为输出信号;c,d均为常数.从式(3)和(4)转换为式(10)和(11),场方程的时域矩阵形式直接变换为一维矢量的运算,所有的电磁场量由一维矢量直接反映出来,该方法在不同维数下的存储变量数与传统FDTD方法的对比结果如表1所示.在满足稳定性条件的前提下,系统矩阵方法比传统FDTD的存储变量数目明显减少,能有效提高计算机的效率.
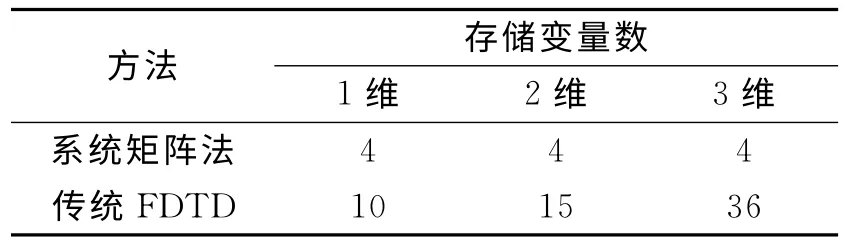
表1 不同维数下系统矩阵方法与传统FDTD的存储变量数
3 无条件稳定的系统矩阵形式
对于式(3)和(4),依据时域离散差分格式来进行处理.由于空间微分的矩阵算子C所对应的场量E和H均为同时刻,导出式(10)和(11)的结果与传统FDTD一样,都需要满足时间离散间隔的稳定性条件.对于无条件稳定的FDTD[7-8],一个计算时间步分为两个过程进行,这里对式(5)中的微分算子C所作用的场量,分别进行时域上的交替处理,需要两个计算过程来描述.为了便于矩阵运算的形式表达,将C分解为

式中:
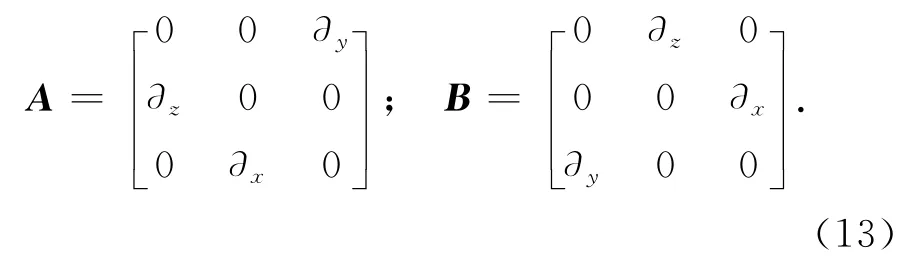
在过程一中,磁场H的时间步在n+1/4,电场E的时间步在n+1/2;过程二中,磁场H的时间步在n+3/4,电场E的时间步在n+1.可得到:
过程一
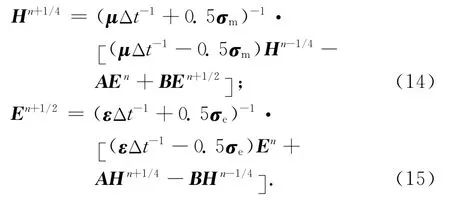
过程二
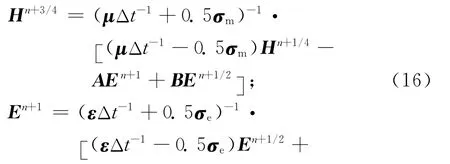

在 过 程 一 中,Hn+1/4和En+1/2都 是 未 知 的,Hn-1/4和En都是已知的,不妨将式(14)代入式(15)中,并将En+1/2的所有项放在等式的左边,令
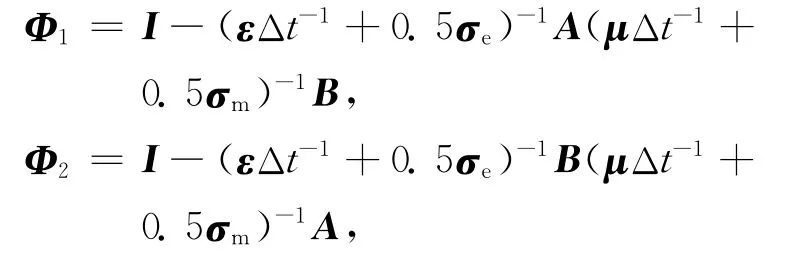
其中I为单位矩阵,可得到
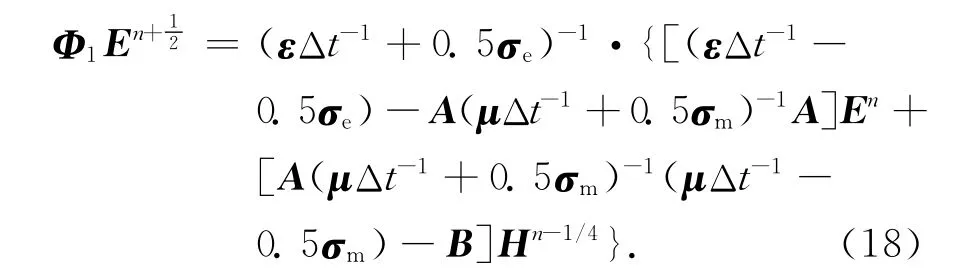
同样,将式(16)代入式(17)中,导出En+1的关系式:
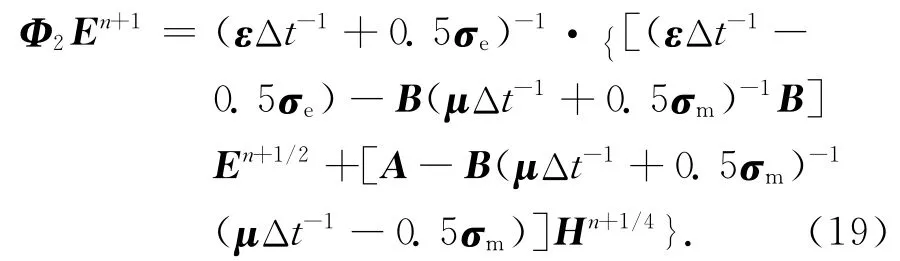
根据式(14)、(18)和(16)、(19)可分别得到对应两个计算过程的系统框图,如图3所示.
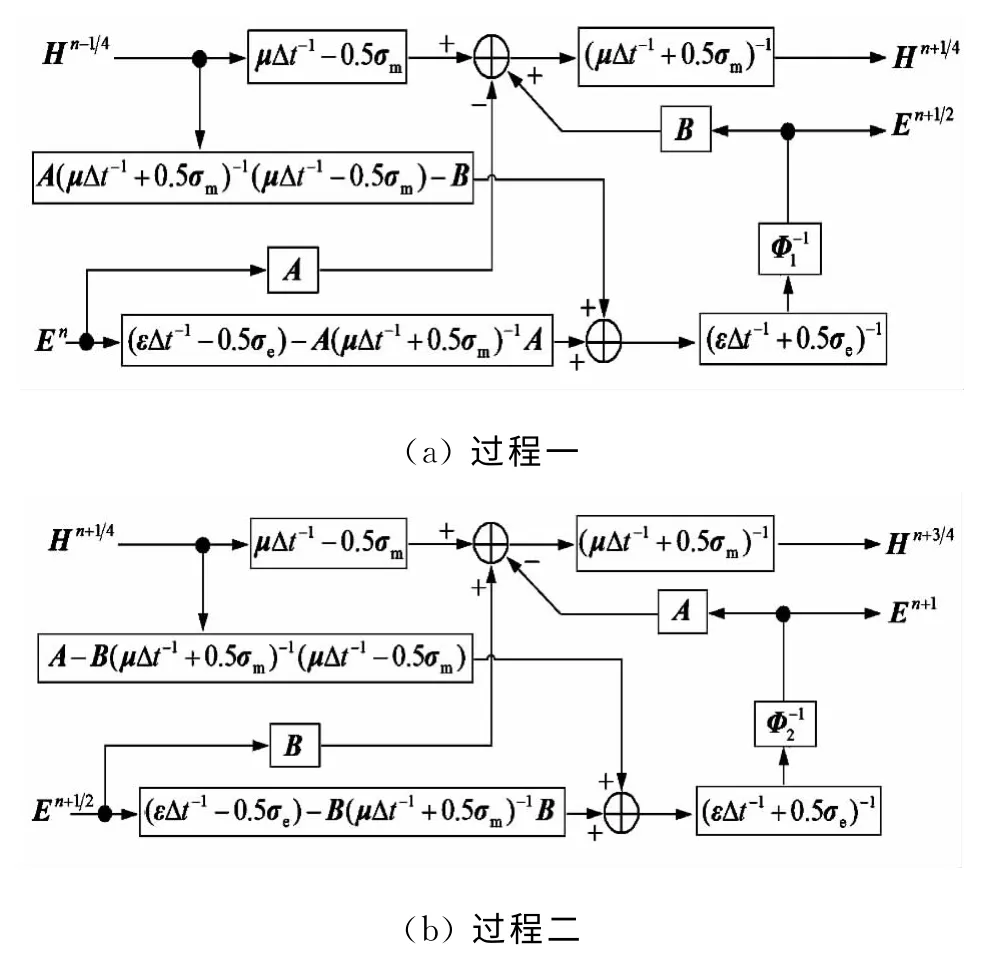
图3 无条件稳定FDTD系统框图
无条件稳定的FDTD系统方程组表示相对较复杂,不妨假设:
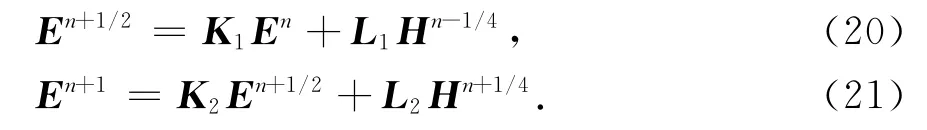
式中K1,L1和K2,L2分别为两个过程对应的系统矩阵R的第一行子矩阵,其表示为:
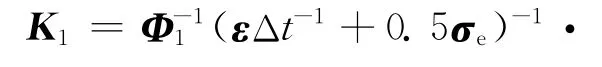

于是式(14)和(16)变换为:
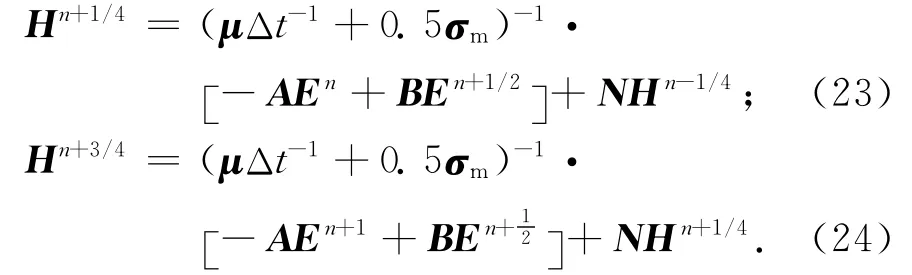
分别将式(23)和(24)中的未知量展开,得:
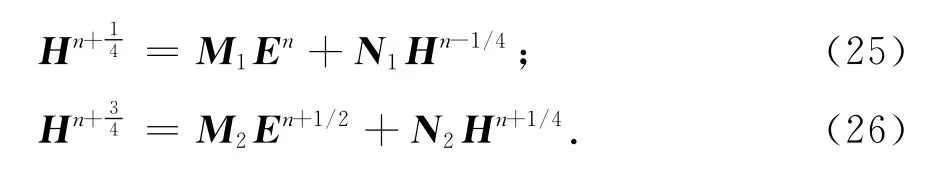
式中M1,N1和M2,N2分别为两个过程对应的系统矩阵R的第二行子矩阵,其表示为:

因此,无条件稳定的FDTD方程组对应的系统矩阵的元素可由式(20)、(21)和(25)、(26)分别表示.由于在各向同性媒质中,Φ1和Φ2均为三条带矩阵,它的求逆运算方法在计算机技术中相当成熟,采用系统矩阵表示的形式,非常便于计算机的编程.
4 数值实验
4.1 一维高斯脉冲的传播
将式(3)和(4)的结果投影在一维空间上进行离散化处理,可得到:
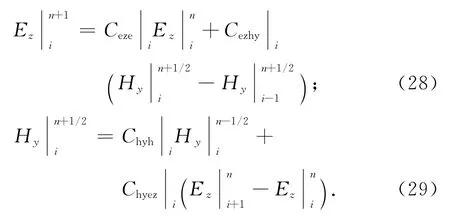
式中
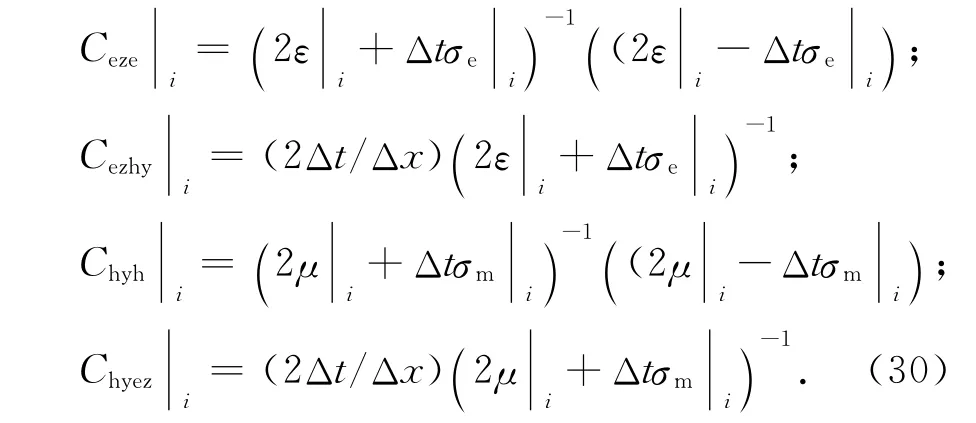
将上述参数初始化,在一维计算区域的中心,设置高斯脉冲形式的电流源为
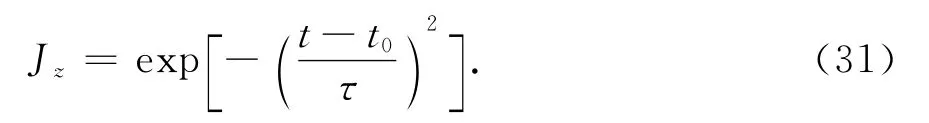
式中:t0=2×10-10;τ=5×10-11.初始化设置Δx=1mm,如图4所示,图中x=0m和x=1m平面为导电壁,实线为电场,虚线为磁场,从图中观察电磁波在一维系统矩阵方法下的仿真过程.电流源从中心处向左右两边传播,碰到导体面后产生反射.
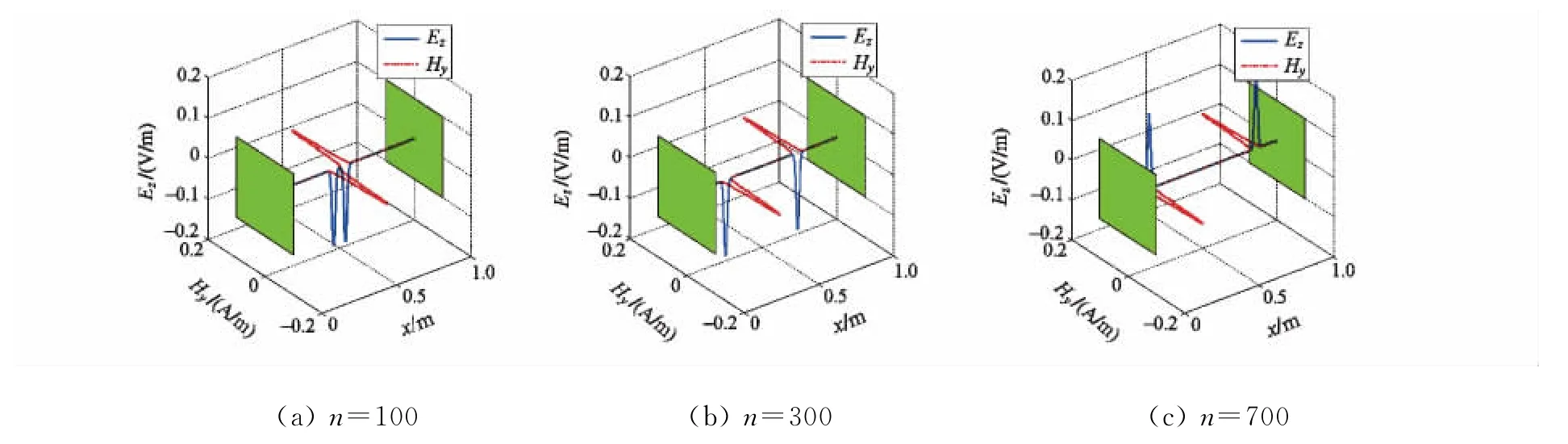
图4 不同时间步的系统矩阵方法动态过程
为了对比系统矩阵方法与传统FDTD的计算效率,采用主频为2.8GHz、双核CPU、内存为4G比特的计算机进行仿真,迭代次数分别设置为1 000和5 000,其计算时间如表2所示.可知,相对传统FDTD,系统矩阵方法的计算效率提高23%.

表2 两种电磁计算方法的时间对比
4.2 低通滤波器
通过式(20)、(21)以及式(25)、(26),得到了在无条件稳定的系统矩阵方法.s为CFL(Courant-Friedrichs-Lewy)因子[7].传统FDTD方法必须满足s≤1的条件,但在无条件稳定的FDTD计算中,s的取值可以大于1.这里以低通滤波器为例,设空间网格尺寸分别为Δx=0.5mm,Δy=0.5mm,Δz=0.3mm,选取接地板尺寸为50Δx×46Δy,介质板的相对介电常数为εr=2.2,其厚度为3Δz=0.9 mm,结构及坐标网格如图5所示.应用传统FDTD方法、ADI-FDTD方法以及系统矩阵方法分别对这种结构的低通滤波器进行计算,结果如表3所示.
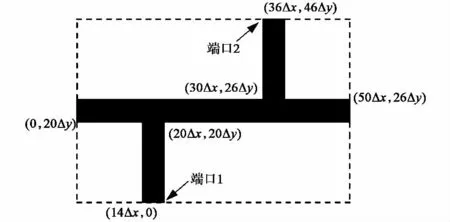
图5 低通滤波器的结构及其尺寸坐标图
传统FDTD方法受Courant稳定性条件的限制,即使CFL因子s=1,其时间步仍需要2 700步才能完成计算.ADI-FDTD方法虽然能够突破Courant稳定性条件的限制,但是计算时间反倒增加了,这种方法并不能减少仿真时间.本文的系统矩阵方法,不受Courant稳定性条件的限制,当s=3时,与传统FDTD方法相比,减少了一半以上的计算时间.图6给出三种方法的仿真结果,系统矩阵方法与ADI-FDTD的结果吻合.同时发现当s=0.9时,它们的结果几乎重合.因ADI-FDTD方法随CFL因子s的增大,Δt也就增大,对应的频率就会减小,因此其频谱响应将会向低频方向移动,图6的散射参数S11曲线也会向低频方向移动.说明本文的系统矩阵方法是有效的.

表3 三种数值方法计算低通滤波器的时间
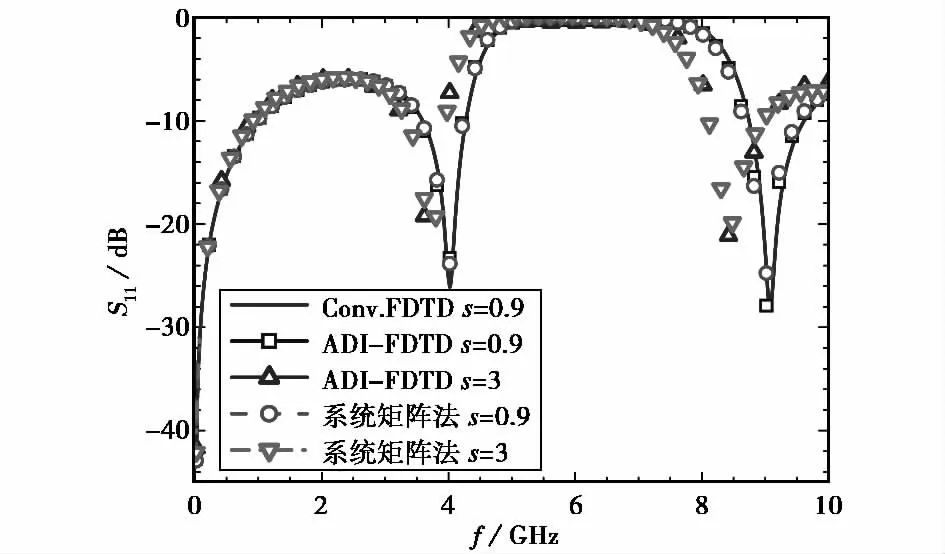
图6 低通滤波器的S11参数
4.3 紧凑型带阻滤波器
为了进一步验证系统矩阵方法的有效性,选取D.Cheng在文献[17]中提出的紧凑型带阻滤波器,其结构如图7所示,其中W3=0.7mm,G=W4=W5=0.5mm,L3=24.2mm,L4=21.1mm和L5=20.6mm.这种结构对于x方向的网格剖分需要更加精细.考虑到L4和L5的长度相近,构成的缝隙至少需要两个网格以上,于是设置网格尺寸为Δx=0.54mm,Δy=0.768mm,Δz=0.114mm,分别采用传统FDTD和本文的方法进行计算.为了更好地说明它的实用性,用商业软件HFSS15.0.2仿真,并将其结果与上述两种方法对比,如图8所示.可知,在CFL因子s取值稍大时,紧凑型带阻滤波器的散射参数S11频率略有移动,但计算结果依然满足要求.说明本文方法与商业软件HFSS15.0.2的仿真结果相媲美.
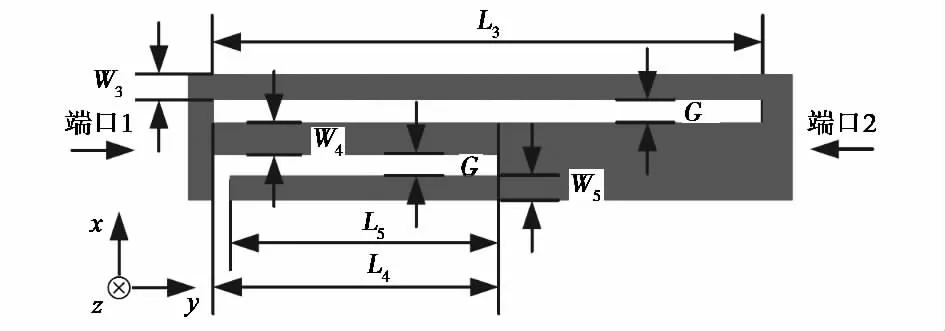
图7 紧凑型带阻滤波器的结构图
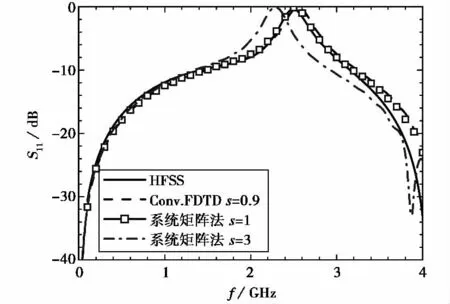
图8 紧凑型带阻滤波器的S11参数
5 结 论
采用系统矩阵方法来研究时域电磁问题,是充分应用DSP的研究成果所提供的计算机软件资源的一次尝试.对于复杂媒质的电磁结构,如复杂目标散射、电磁兼容设计等,针对具体的物理模型,利用DSP技术建立系统矩阵是一个相对容易的工作.通过系统传递函数的拉普拉斯反变换,建立时域系统矩阵,从而求解这个系统方程,是今后进一步开展的工作.上述算例均表明本文的方法是有效的,能够显著提高计算效率.
[1]吴 霞,周乐柱.时域有限元在计算电磁问题上的应用及发展[J].电波科学学报,2008,23(6):1209-1216.WU Xia,ZHOU Lezhu.Application and development of time-domain finite element method on EM analysis[J].Chinese Journal of Radio Science,2008,23(6):1209-1216.(in Chinese)
[2]JIN J M,LOU Z,LI Y J,et al.Finite element analysis of complex antennas and arrays[J].IEEE Transactions on Antennas and Propagation,2008,56(8):2222-2240.
[3]唐 璞,王 建,王超然,等.曲线分段的矩量法分析阿基米德平面螺旋天线[J].电波科学学报,2006,21(6):929-934.TANG Pu,WANG Jian,WANG Chaoran,et al.Analysis of archimedean spiral antenna using moment method with curved segmentations[J].Chinese Jour-nal of Radio Science,2006,21(6):929-934.(in Chinese)
[4]张小林,高火涛.近地短波鱼骨天线矩量法建模及应用[J].电波科学学报,2007,22(2):281-285.ZHANG Xiaolin,GAO Huotao.Moment method modeling and application for shortwave fishbone antennas above ground[J].Chinese Journal of Radio Science,2007,22(2):281-285.(in Chinese)
[5]YEE K S,Numerical solution of initial boundary value problem involving Maxwell’s equations in isotropic media[J].IEEE Transactions on Antennas and Propagation,1966,14(3):302-307.
[6]葛德彪,闫玉波.电磁波时域有限差分方法[M].3版.西安:西安电子科技大学出版社,2011.
[7]NAMIKI T.A new FDTD algorithm based on alternating direction implicit method[J].IEEE Transactions on Microwave Theory and Techniques,1999,47(10):2003-2007.
[8]ZHENG F,CHEN Z,ZHANG J.A finite-different time-domain method without the courant stability condition[J].IEEE Microwave Guided Wave Letter,1999,9(11):441-443.
[9]张玉强,葛德彪.一种基于数字信号处理技术的改进通用色散介质移位算子时域有限差分方法[J].物理学报,2009,58(12):8243-8248.ZHANG Yuqiang,GE Debiao.An improved shift operator finite-difference time-domain method based on digital signal processing technique for general dispersive medium[J].Acta Physica Sinica,2009,58(12):8243-8248.(in Chinese)
[10]葛德彪,吴跃丽,朱湘琴.等离子体散射FDTD分析的移位算子方法[J].电波科学学报,2003,18(4):359-362.GE Debiao,WEI Yueli,ZHU Xiangqin.Shift operator method applied for dispersive medium in FDTD analysis[J].Chinese Journal of Radio Science,2003,18(4):359-362.(in Chinese)
[11]汪 彤,张文俊,刘维亮.N阶色散媒质的FDTD法与数字信号处理技术[J].电波科学学报,2000,15(1):455-458.WANG Tong,ZHANG Wenjun,LIU Weiliang.FDTD and digital signal processing for the Nth-order dispersive media[J].Chinese Journal of Radio Science,2000,15(1):455-458.(in Chinese)
[12]陈春雨,吴 群.基于系统函数的FDTD特性研究[J].微波学报,2010,26(5):53-55.CHEN Chunyu,WU Qun.Study on characteristics of FDTD based on system function[J].Journal of Microwaves,2010,26(5):53-55.(in Chinese)
[13]ALAN V O,ALAN S W,HAMID N,et al.Signals and Systems[M].2nd ed.New York:Pearson Education,2013.
[14]吴迎年,张 霖,张利芳,等.电磁环境仿真与可视化研究综述[J].系统仿真学报,2009,21(20):6332-6338.WU Yingnian,ZHANG Lin,ZHANG Lifang,et al.Survey on electromagnetic environment simulation and visualization[J].Journal of System Simulation,2009,21(20):6332-6338.(in Chinese)
[15]殷 勤,陈 彬,汪 莹,等,电磁跟踪系统磁传感器性能的数值模拟研究[J].传感技术学报,2010,23(8):1079-1083.(in Chinese)YIN Qin,CHEN Bin,WANG Ying,et al.Study on numerical simulation of electromagnetic tracker system magnetic sensor[J].Chinese Journal of Sensors and Actuators,2010,23(8):1079-1083.(in Chinese)
[16]王一平.工程电动力学(修订版)[M].西安:西安电子科技大学出版社,2005.
[17]CHENG D,YIN H C,ZHENG H X.A compact dual-band bandstop filter with defected microstrip slot[J].Journal of Electromagnetic Waves and Applications,2012,26(10):1374-1380.

