自适应粒子群神经网络交通流预测模型

许榕,周东,蒋士正,陈启美

(南京大学电子科学与工程学院, 210023, 南京)



自适应粒子群神经网络交通流预测模型

许榕,周东,蒋士正,陈启美

(南京大学电子科学与工程学院, 210023, 南京)

针对传统神经网络预测模型预测结果准确性低且存在大量无效迭代的问题,提出了自适应权重粒子群神经网络交通流预测(PSOA-NN)模型。首先根据待预测点的上下游观测点数和历史数据,随机初始化若干组模型参数并计算每组参数对应粒子的适应度;然后采用改进的sigmoid函数替代原有模型中的固定惯性权重,并根据其中适应度变好的粒子更新粒子速度和位置,一直迭代到粒子适应度小于预设值为止;最后将满足条件粒子对应的模型参数应用到神经网络模型,根据实时交通流数据预测出15 min后的数据。仿真结果表明,使用PSOA-NN模型,可使得在同等预测误差范围内收敛速度提升0.6～1.7倍。

交通流;预测;粒子群优化;神经网络

当前,在智能交通系统(ITS)领域中,短时交通流预测已处于核心地位,它能够提供实时有效的信息,有助于出行者进行路径选择,节约出行时间,也有助于交通管理者采取合适的交通诱导措施,提高路网的运行效率和安全性,变被动应对为主动管理[1]。

目前,常见的交通流预测模型有基于时间序列的ARIMA模型、卡尔曼滤波模型、支持向量回归模型以及神经网络模型等。ARIMA模型和卡尔曼滤波模型都属于线性模型,而交通流是动态的、非线性的、不确定的系统,因此该模型往往达不到令人满意的效果[2-3]。支持向量回归模型适合小样本的快速预测,对核函数比较敏感[4],而神经网络凭借其良好的处理非线性问题能力,已经广泛应用到工程之中[5-7],其中以反向传播(BP)算法训练神经网络模型最为流行。然而,BP神经网络却存在着一些固有的缺陷[8],如收敛速度慢、容易陷入局部最优、针对已知问题选择网络规模困难等。粒子群优化(PSO)算法是一种基于群体智能的优化算法,凭借其全局寻优、参数配置简单等优点大量使用在模型优化之中[9]。使用PSO算法优化神经网络模型,可加快模型收敛速度寻找全局最优。PSO优化算法在神经网络预测模型中运用已十分广泛[10-12],如PSO优化双层RBF神经网络模型[13]、PSO优化混沌BP神经网络[14]等,它们往往只是针对传统PSO算法的简单应用,而改进主要体现在对神经网络模型的优化之上,并未对PSO算法本身进行优化。传统的PSO算法虽然可以加快原有神经网络的收敛速度,但其训练过程中仍存在许多无效的迭代。

针对上述问题,本文通过分析BP神经网络模型和传统PSO算法,根据每个粒子的历史状态和迭代次数,改变PSO算法中的惯性权重因子,降低无效惯性分量带来的影响,从而提高神经网络的收敛速度和模型精度。

1 神经网络和粒子群算法

1.1 BP神经网络模型

神经网络由多个神经元构成,多个神经元可以组成一层进行并行学习,然后在层与层之间进行信息的传递。BP神经网络,主要是用于解决3层神经网络结构中的隐层单元无法直接计算误差的问题,它将传输层误差以从后向前的方式逐层传递,最终间接的计算出隐层的误差。整个算法分为2个阶段:正向过程和反向过程。其中,正向过程完成将输入信息从输入层经隐层向后逐层传递并计算各单元的输出值,反向过程将输出误差逐层向前传递从而计算出隐层各单元的误差并用此误差修正前层权值。

基于神经网络模型的预测原理为:用一部分数据训练模型,即确定网络结构(包括隐含层数、各层节点数、各层连接权值、各层神经元的传递函数),网路结构确定以后,再用实时数据进行预测。与卡尔曼滤波不同,神经网络可以离线训练,这样就减少了在线预测的计算量[15]。

一个简单的基于神经网络的预测模型如图1所示,Xs(t)为路段某一断面s上t时刻的交通流向量。考虑到路段的长度和交通流的特性,采用当前时间段和前m个时间段的交通流量对未来时间段的交通流量进行预测,将Xs(t),Xs(t-1),…,Xs(t-m)作为输入样本,Xs(t+1)作为输出值。然而,单点交通流预测仅考虑了该点的历史交通流数据,并没有考虑上下游观测点交通流所提供的相关信息,而实际上,在整个交通网络中,上下游的交通流是相互影响的。因此,现有改进的神经网络预测模型是将{Xs(t),Xs(t-1),…,Xs(t-m)},{Xs+1(t),Xs+1(t-1),…,Xs+1(t-m)},…,{Xs+n(t),Xs+n(t-1),…,Xs+n(t-m)}作为输入样本,Xs(t+1)作为输出值。Nin、Nmid、Nout分别表示输入层、隐藏层和输出层结点数目,那么神经网络共有Ntotal个模型参数需要通过粒子群优化算法确定

(1)

神经网络权重和阈值均是需要在神经网络训练时确定的,而这些参数可以通过粒子群优化算法获得。

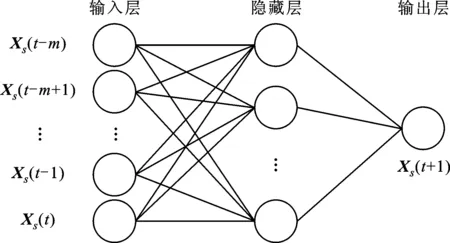
图1 基于神经网络的简单预测模型

1.2 标准PSO优化神经网络

PSO算法是以鸟群捕食行为为原型建立的一种快速搜索模型。

假设第i个粒子为Xi=[xi1,xi2,…,xiS]T,表示粒子i在S维空间里的位置(方程潜在的解),则n个粒子组成的种群可表示为X=(X1,X2,…,Xn)。粒子的适应度值是由目标函数根据粒子所处位置计算得出。第i个粒子的速度记为Vi=[Vi1,Vi2,…,ViS]T,则其个体历史最优值记为Pi=[Pi1,Pi2,…,PiS]T,全局历史最优值记为Pg=[Pg1,Pg2,…,PgS]T。每个粒子根据个体最优值和全局最优值更新它们的速度和位置,速度更新方程(惯性分量、自我学习分量和社会学习分量之和)和位置更新方程分别为

(2)

(3)

式中:wI为惯性权重;d=1,2,…,S;i=1,2,…,n;k为迭代次数;Vid为粒子的速度;c1和c2为加速因子;rand为随机函数。

使用PSO算法可以实现对神经网络模型结构和模型参数的优化。理论上,3层模型能以任意精度逼近一个连续函数,而PSO优化主要是针对模型参数的优化。神经网络模型需要优化的参数包括:输入层第i个结点到隐藏层第j个结点的权重wij,隐藏层第j个结点到输出层第h个结点的权重wjh,输入层所有结点到隐藏层第j个结点经加权求和后的阈值bj,以及隐藏层所有结点到输出层第h个结点经加权求和后的阈值bh。其中,输入层到隐藏层的权值有NinNmid个,隐藏层到输出层的权值有NmidNout个,输入层到隐藏层的阈值有Nmid个,隐藏层到输出层间的阈值有Nout个,共计Ntotal个,如式(1)所示。在PSO算法中,粒子的每一维空间与Ntotal个需要优化的参数一一对应,即S=Ntotal。

2 改进的PSO算法及预测流程

2.1 自适应权重粒子群算法

标准的PSO算法中,使用大量粒子参与迭代以尽快找到最优解。所有粒子使用相同的惯性权重,必将导致部分粒子为了使其他粒子达到最优值,朝着不利于自身的方向运动。而如果每次迭代的惯性分量各个粒子均根据上一次迭代结果进行调整,这将会加快PSO算法收敛速度。自适应权重粒子群(PSOA)的权重改进如下

(4)

式中:f(·)为适应度函数;Δf(Wi,k)=f(Wi,k)-f(Wi,k);wB为基础权重。

以二维空间中粒子运动为例,自适应权重PSO算法如图2所示。将搜索空间中粒子分为两类,vt1和vt2分别表示适应度值变大(差)和适应度值变小(好)的惯性分量,α为学习分量。如果粒子上一次适应度变差,说明其惯性分量应该舍弃,最终的速度应等于学习分量a(wI=0);否则惯性权重和其他粒子一样最终速度为wIvt2+a。

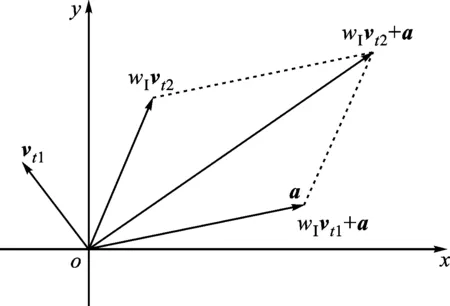
图2 自适应权重PSO算法示意图

传统的PSO算法,速度更新函数中惯性分量的权重wI为一固定值(通常为1)。如果权重设定过大,往往会导致优化后模型的参数不准确;反之,则会导致迭代次数变多,增加训练时耗。为了解决这一矛盾,通常会将wI设定为一个随迭代次数线性减小的变量。

为了更好地兼顾PSO算法的速度和精度,在迭代的前期应使用较大的权重以保证收敛速度;而后期应使用细粒度的权重来提高收敛精度。因而,本文提出的自适应权重粒子群优化(PSOA)算法,使用改进的sigmoid函数(简称sigmoid_a函数)替代原有的线性递减函数作为基础权重wB,计算如下

(5)

式中:ksmooth为平缓度,本文取ksmooth=0.1;λ为权重最大值/权重初始值,本文取λ=1.5;i和imax分别为当前迭代次数和最大迭代次数。

2.2PSOA-NN模型

本文使用PSOA算法优化神经网络的交通流预测(PSOA-NN)模型流程如图3所示。流程共分为两部分:①使用PSOA算法对神经网络进行离线训练;②使用离线训练得到的模型参数对实时数据进行预测。PSOA-NN模型流程如下:

(1)根据预先定义的神经网络规模随机初始化M个Ntotal维粒子,每一维度均代表神经网络模型的一个参数;

(2)使用神经网络预测函数nn_predict返回值的平方和误差(error sum of squares,SSE)作为适应度函数,计算所有粒子的适应度;

(3)根据粒子的自身历史(和其他粒子)的适应度,更新个体最优(和全局最优);

(4)按照式(4)和式(5)制定的自适应权重更新规则计算每个粒子对应的wB值;

(5)依据计算出的wB值,重新计算粒子的速度,并更新粒子的位置;

(6)判断迭代是否达到终止条件:粒子的适应度函数值<ε或者迭代次数达到预定的最大迭代次数,若未达到条件返回步骤(2)继续下一次迭代,否则将全局最优的粒子作为神经网络模型的参数;

(7)输入实时交通流数据,使用步骤1～步骤6获得的模型参数进行预测,得到预测结果。

图3 PSOA-NN模型流程图

3 性能测试

3.1PSOA-NN预测交通流

MATLAB实验数据来自于美国加利福利亚州公路局PeMS系统[16],选取洛杉矶市附近的高速公路82个检测器,时间从2013年3月4日至2013年3月17日,如图4所示。实时数据由间隔30 s的环形线圈检测得到,并经过PeMS系统整合为间隔5 min数据,每个采集点共4 032条数据记录,包含车流高峰与空闲时刻的均速、流量等。实验使用这两周工作日的数据,包括每天的早高峰、晚高峰以及空闲时刻的交通数据,第一周工作日数据用来训练,第二周工作日数据用来预测。实验采用平均绝对百分误差(mean absolute percentage error,MAPE)衡量预测的准确率,如下式

(6)

模型的预测过程分为两部分:离线模型训练和在线实时预测。在预测速度和流量的实验中,文中提到的优化算法均能提高模型的收敛速度和精度。为能简明突出算法的改进,本文采用5 min内经过车辆的平均速度作为预测自变量。任取一点(桩号:VDS 718421)速度的预测结果进行展示,如图5所示。

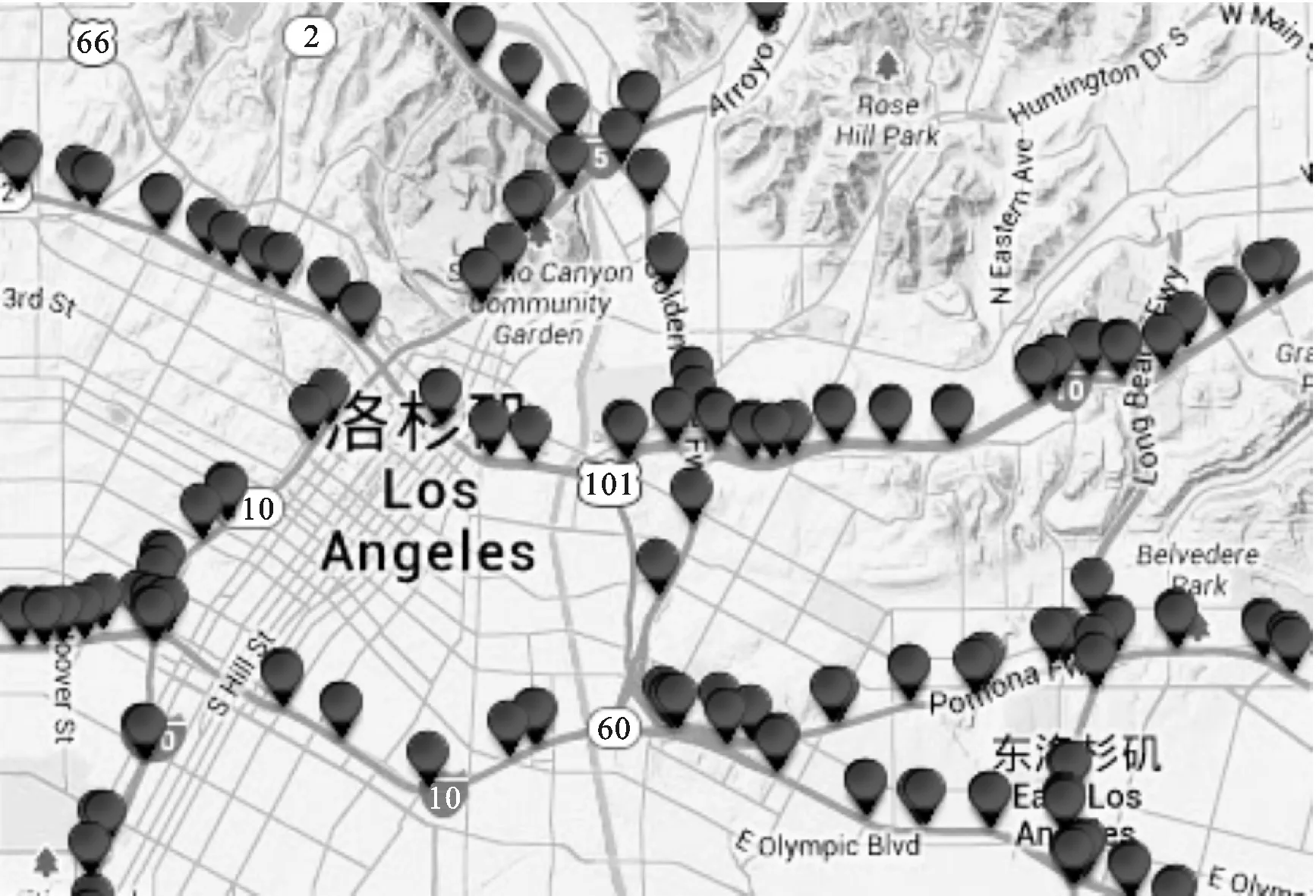
图4 数据检测点对应图

模型的输入为当前时刻前15 min的3组历史数据,预测15 min后的均速。图5分别展示了一天的预测结果和预测误差,其中实线为实际值,虚线为预测值。通过观察可以发现:预测15 min后的车速误差大部分在10 m/h内,而在200点附近出现了剧烈的振荡。车速的急剧变化是由于晚高峰导致,而神经网络模型本身不能适应快速变化的交通预测。此外,晚高峰车速较低也是导致相对误差变大的原因。

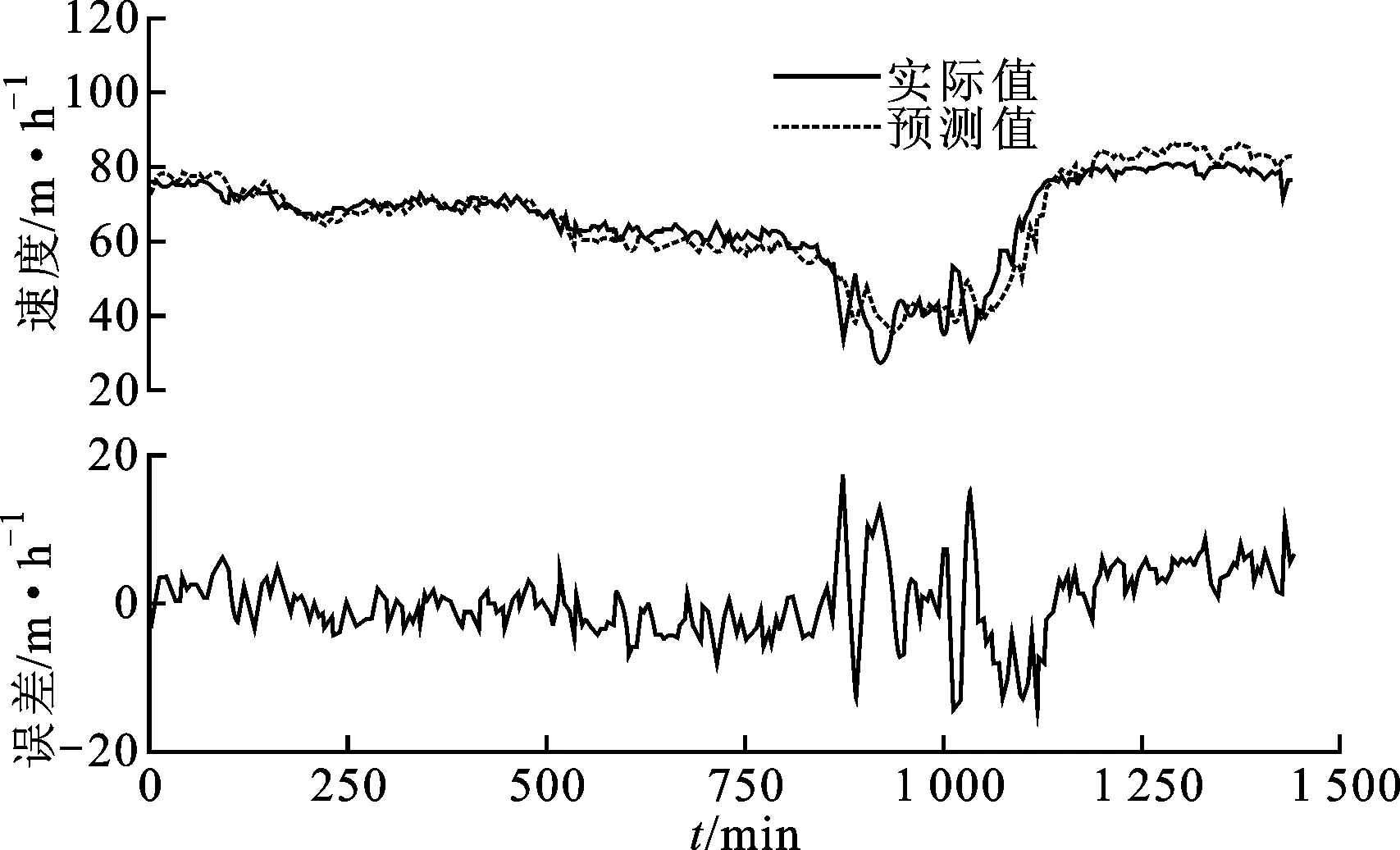
图5 PSOA-NN模型预测结果

3.2 模型性能分析

神经网络的训练方法有两大类:①根据神经网络原理训练,例如BP神经网络(简称BP-NN);②使用生物学方法训练,例如PSO优化神经网络、遗传算法优化神经网络(简称GA-NN)等。PSO算法依据权重变化分为固定权重(简称PSOC)、sigmoid_a权重(简称PSOS)、自适应权重(简称PSOA),对应的优化神经网络模型分别记为PSOC-NN和PSOA-NN。

PSO算法和GA算法均属于经典的智能优化算法。GA和PSO具有类似的运算过程:首先,随机初始化种群;然后,计算种群里面每个个体的适应度,适应度反映了最优解的距离;最后,种群根据适应度进行演绎,一直到满足条件位置。两者的区别主要体现在种群的演绎过程,GA算法的演绎过程(遗传操作)包括选择、交叉和变异,而PSO算法的演绎则是根据自我学习分量和全局学习分量。GA算法根据上一代进行优化,用染色体实现信息共享,因而整个种群呈现相对均匀的速度移向最优解。在PSO算法中使用全局学习分量更新粒子的状态(速度和方向),所有粒子会更快地收敛于最优解。

图6为3种PSO算法优化神经网络模型、BP神经网络模型、遗传算法优化神经网络预测σMAPE随迭代次数的变化图。从图中可以看出:随着迭代次数的增加,模型预测σMAPE均呈现下降的趋势。虽然,BP神经网络模型受限于算法本身,经过100次迭代并未使σMAPE降低到理想状态。遗传算法对应的预测σMAPE呈现匀速下降过程,经过49次迭代后基本稳定在11%,而PSO算法优化神经网络模型的σMAPE在不到20次的迭代后,已经达到了一个相对较小值。与遗传算法相比,PSO算法的整个搜索更新取决于全局最优解,因而粒子会更快地收敛于最优解。由此可见,PSO优化算法可以提高BP神经网络模型的精度。

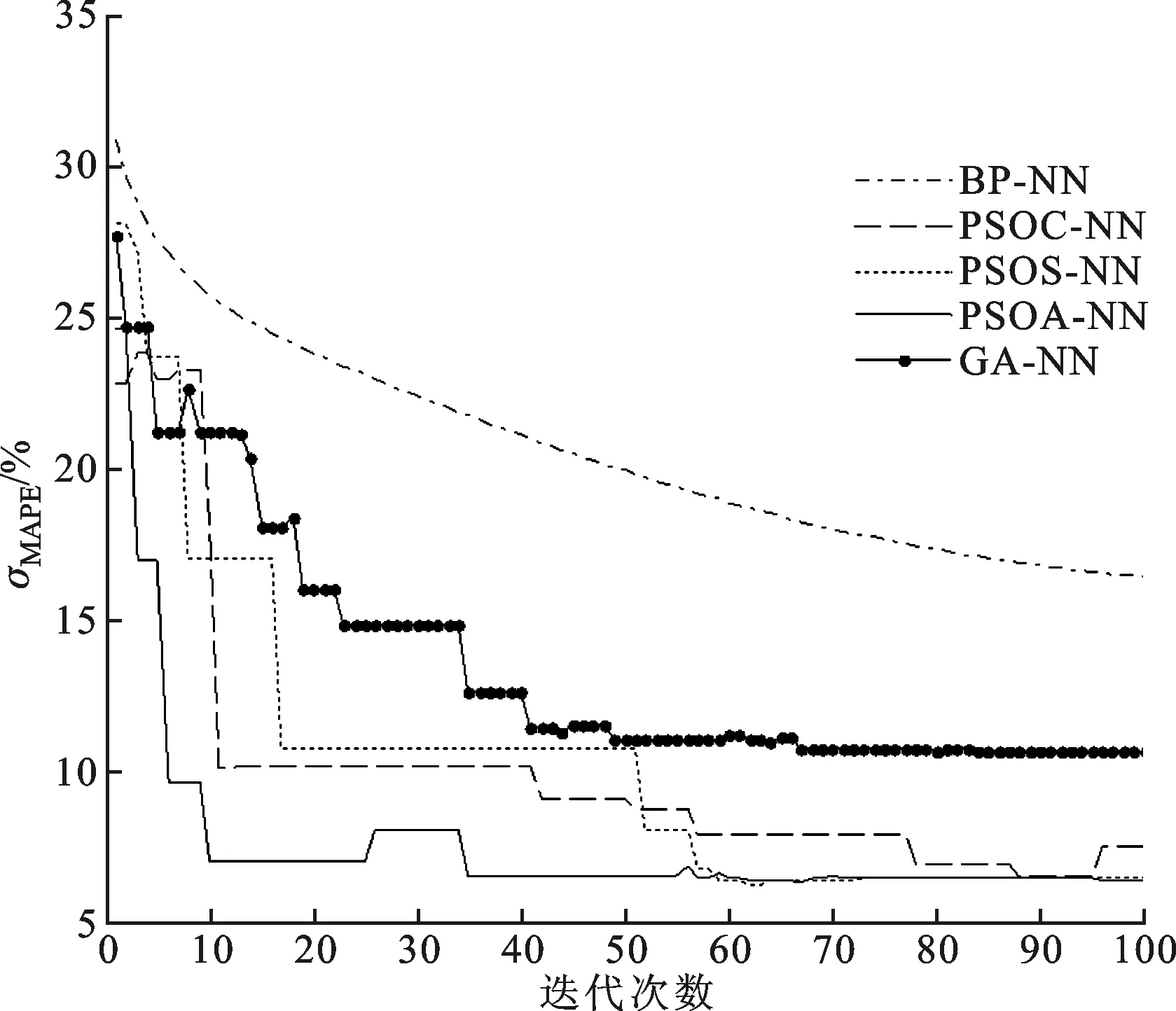
图6 4种预测模型MAPE随迭代次数的变化

在100次迭代后,PSOS和PSOA算法比PSOC算法获得了更低的σMAPE。可见,使用sigmoid_a函数可以获得更高的精度。在第10次迭代之后,PSOA算法的σMAPE已经下降到9.6%,而另外两种优化算法到第52次迭代之后才降到此值。可见,PSOA算法比PSOC和PSOS算法有更快的收敛速度。此外需要说明的是:因为适应度函数SSE和误差σMAPE不同,导致PSOA在迭代25次时σMAPE存在小幅上升。

实验采用交通流速度作为预测变量。由于速度大部分集中在一定范围之内,而流量则分布在更大的范围之内,所以,出现神经网络预测比流量预测σMAPE高一些。传统的神经网络使用的是固定步长接近最优解,固然不能达到更低的σMAPE。文中提出的PSOA优化算法,将标准的PSO算法中的惯性权重wI使用改进的sigmoid函数来代替,使用该方法能够很好地降低预测σMAPE。

平均迭代次数是表示算法成功收敛的平均迭代次数,反映了算法的收敛速度。表1为GA和PSO算法优化模型的预测MAPE分别达到85%和90%所需的平均迭代次数。从表1中可以看出:σMAPE从85%提高到90%需要增加1倍以上的迭代次数,GA算法的平均迭代次数和未改进的PSO算法相近,而PSOA算法在达到相同的精度情况下所需迭代次数均远少于其他同类算法,收敛速度提升0.6～1.7倍;PSOC算法中粒子移动会受到适应度值变差惯性分量的影响,因而导致其平均迭代次数略高于GA算法;PSOA算法舍去了适应度值变差惯性分量的影响,从而加快了收敛速度。

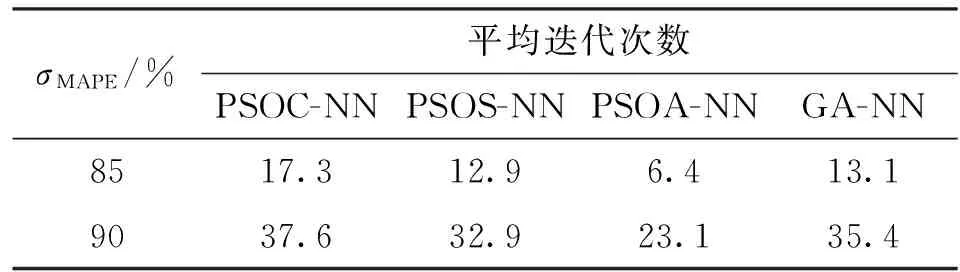
表1 4种算法的平均迭代次数比较

选定路网中82个观测点预测结果的误差棒如图7所示,“工”型的中点代表平均σMAPE,“工”型上下端则表示σMAPE标准差(为了方便展示,实际上是标准差的0.05倍)。GA算法优化的神经网络模型预测误差均值在9%附近,而PSO及其改进算法优化的神经网络模型预测误差则在6%附近。可见,PSO算法的优化效果明显高于GA算法。对于PSO算法,由于PSOA和PSOS算法引入了改进的sigmoid函数,其平均σMAPE小于PSOC算法。

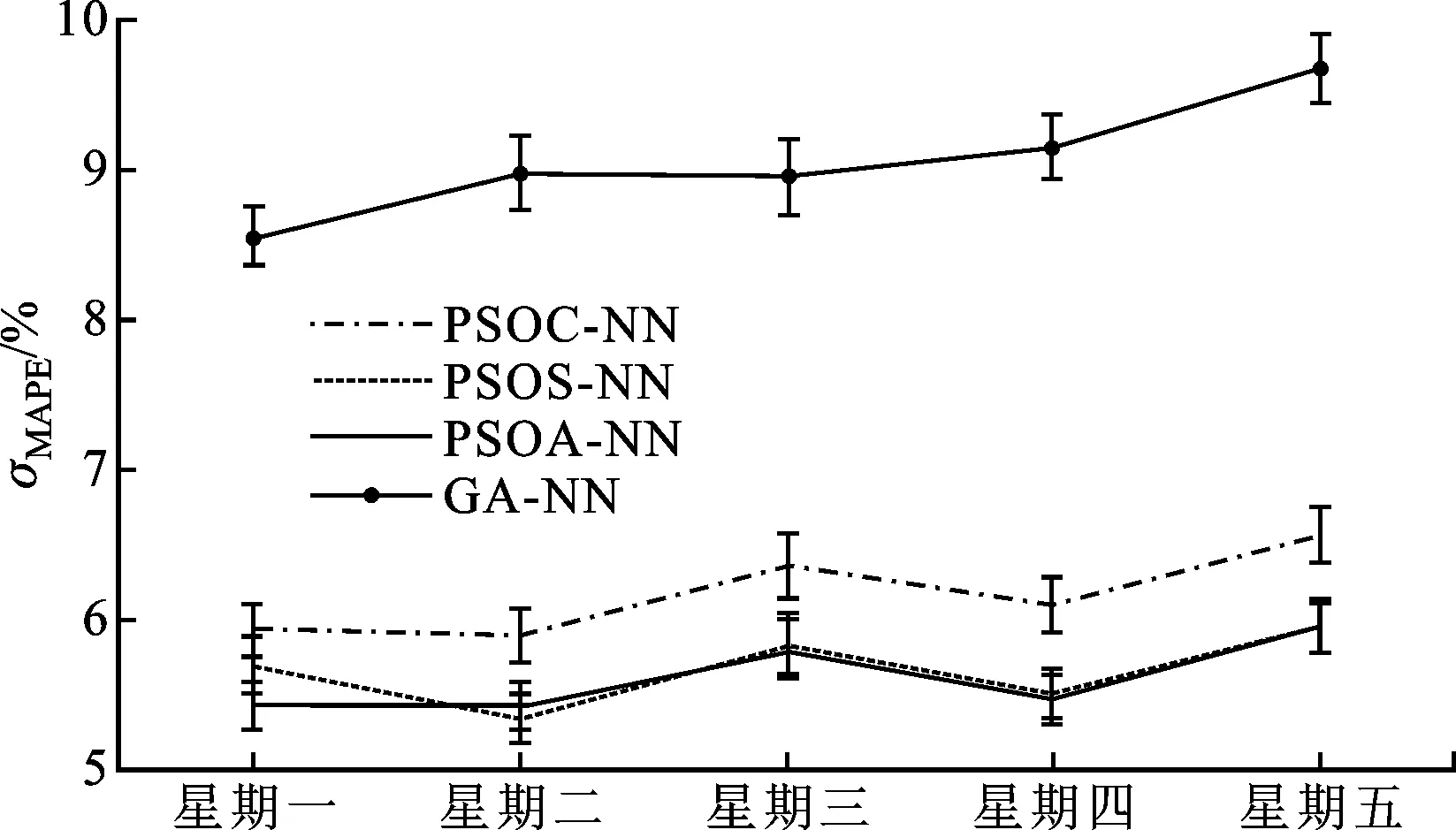
图7 平均预测误差图

由此可见,采用sigmoid_a函数对惯性权重优化可以提高其精度。PSOA算法采用了sigmoid_a函数对惯性权重优化,并对其进行了自适应改进,不仅提高了神经网络模型的精度,而且加快了模型的收敛速度。

4 结 论

仿真测试结果表明,以sigmoid_a函数作为基础惯性权重,可以提高神经网络模型的精度;使用自适应粒子群算法优化神经网络模型,可以加快收敛速度。

由此可见,使用PSOA算法优化神经网络模型,提高了神经网络模型的精度和收敛速度。

[1] 王进, 史其信. 短时交通流预测模型综述 [J]. 中国公共安全: 学术版, 2005, 1(6): 92-98. WANG Jin, SHI Qixin. Short term traffic flow forecasting model review [J]. China Public Security: Academy Edition, 2005, 1(6): 92-98.

[2] 贺国光, 李宇, 马寿峰. 基于数学模型的短时交通流预测方法探讨 [J]. 系统工程理论与实践, 2000(12): 51-56. HE Guoguang, LI Yu, MA Shoufeng. Discussion on short-term traffic flow forecasting methods based on mathematical models [J]. Systems Engineering: Theory & Practice, 2000(12): 51-56.

[3] 许岩岩, 翟希, 孔庆杰, 等. 高速路交通流短时预测方法 [J]. 交通运输工程学报, 2013, 13(2): 114-119. XU Yanyan, ZHAi Xi, KONG Qingjie, et al. Short-term prediction method of freeway traffic flow [J]. Journal of Traffic and Transportation Engineering, 2013, 13(2): 114-119.

[4] The Transportation Research Boards. Highway capacity manual [M]. Washington, DC, USA: National Research Council, 2000: 26-27

[5] HASEGAWA M, WU G, MIZUNI M. Applications of nonlinear prediction methods to the internet traffic [C]∥The 2001 IEEE International Symposium on Circuits and Systems. Piscataway, NJ, USA: IEEE, 2001: 169-172.

[6] 林军, 倪宏, 孙鹏, 等. 一种采用神经网络PID控制的自适应资源分配方法 [J]. 西安交通大学学报, 2013, 47(4): 112-117, 136. LIN Jun, NI Hong, SUN Peng, et al. Adaptive resource allocation based on neural network PID control [J]. Journal of Xi’an Jiaotong University, 2013, 47(4): 112-117, 136.

[7] 高瑞鹏, 尚春阳, 江航. 遗传算法结合小波神经网络的列车车轮扁疤故障检测方法 [J]. 西安交通大学学报, 2013, 47(9): 88-91, 111. GAO Ruipeng, SHANG Chunyang, JIANG Hang. A fault detection strategy for wheel flat scars with wavelet neural network and genetic algorithm [J]. Journal of Xi’an Jiaotong University, 2013, 47(9): 88-91, 111.

[8] VENAYAGAMOORTHY G K. Online design of an echo state network based wide area monitor for a multimachine power system [J]. Neural Networks, 2007, 20(3): 404-413.

[9] 赵建华, 张陵, 孙清. 利用粒子群算法的传感器优化布置及结构损伤识别研究 [J]. 西安交通大学学报, 2015, 49(1): 79-85. ZHAO Jianhua, ZHANG Ling, SUN Qing. Optimal placement of sensors for structural damage identification using improved particle swarm optimization [J]. Journal of Xi’an Jiaotong University, 2015, 49(1): 79-85.

[10]ZHU Y, ZHANG G, QIU J. Network traffic prediction based on particle swarm BP neural network [J]. Journal of Networks, 2013, 8(11): 2685-2691.

[11]ZHANG H, ZHAO G, CHEN L, et al. Short-term prediction of wind power based on an improved PSO neural network [J]. TELKOMNIKA Indonesian Journal of Electrical Engineering, 2014, 12(7): 4973-4980.

[12]ZHANG K, LIANG L, HUANG Y. A network traffic prediction model based on quantum inspired PSO and neural network [C]∥2013 Sixth International Symposium on Computational Intelligence and Design. Piscataway, NJ, USA: IEEE, 2013: 219-222.

[13]ZHAO J, JIA L, CHEN Y, et al. Urban traffic flow forecasting model of double RBF neural network based on PSO [C]∥Sixth International Conference on Intelligent Systems Design and Applications, 2006. Piscataway, NJ, USA: IEEE, 2006: 892-896.

[14]LI S, WANG L, LIU B. Prediction of short-term traffic flow based on PSO-optimized chaotic BP neural network [C]∥2013 International Conference on Computer Sciences and Applications. Piscataway, NJ, USA: IEEE, 2013: 292-295.

[15]李松, 刘力军, 解永乐. 遗传算法优化BP神经网络的短时交通流混沌预测 [J]. 控制与决策, 2011, 26(10): 1581-1585. LI Song, LIU Lijun, XIE Yongle. Chaotic prediction for short-term traffic flow of optimized BP neural network based on genetic algorithm [J]. Control and Decision, 2011, 26(10): 1581-1585.

[16]California Department of Transportation. Caltrans PeMS[EB/OL]. [2014-02-18]. http: ∥pems.dot.ca.gov/?dnode=search&content=cnt_search&view=e.

(编辑 刘杨)

A Traffic Forecasting Model Using Adaptive Particle Swarm Optimization Trained Neural Network

XU Rong,ZHOU Dong,JIANG Shizheng,CHEN Qimei

(School of Electronic Science and Engineering, Nanjing University, Nanjing 210023, China)

A novel traffic forecasting model using particle swarm optimized neural network with adaptive weights (PSOA-NN) is proposed to address the issue of low accuracy prediction of traditional neural network forecasting model with a lot of invalid iterations in prediction process. Several groups of model parameters are initialized casually according to the observing point numbers of up and down streams and historical data in a neighbourhood of the forecast location, and the particle fitness of corresponding parameters in each group is calculated. Then, an improved sigmoid function is used to replace the fixed inertia weights in original model, speeds and locations are updated for the particles with improved fitness, and the iteration continues until the fitnesses of particles are less than a preset value. Finally, the model parameters that satisfies particle requirement are applied to the neural network model, and the traffic data 15 min later is predicted according to real time traffic flow data. Simulation results show that the convergent speed of the PSOA-NN model increases by about 0.6 to 1.7 times within the identical deviation range.

traffic flow; forecasting; particle swarm optimization; neural networks

2015-02-20。

许榕(1991—),男,硕士生;陈启美(通信作者),男,教授,博士生导师。

国家自然科学基金资助项目(61105015);国家科技重大专项课题资助项目(2012ZX03005-004-003)。

时间:2015-07-23

10.7652/xjtuxb201510017

TP183

A

0253-987X(2015)10-0103-06

网络出版地址:http://www.cnki.net/kcms/detail/61.1069.T.20150723.0922.004.html